电气工程学报, 2021, 16(2): 141-148 doi: 10.11985/2021.02.018

电力系统

面向分布式电源的改进GWO-GS电网承载力提升方法*

许翰宸,1, 王立辉,2, 廖宇航,2

1.南京工程学院电力工程学院 南京 211167

2.东南大学仪器科学与工程学院 南京 210096

Method of Improving Power Grid Hosting Capacity for Distributed Generation Based on Improved GWO-GS

XU Hanchen,1, WANG Lihui,2, LIAO Yuhang,2

1. School of Electric Power Engineering, Nanjing Institute of Technology, Nanjing 211167

2. School of Instrument Science and Engineering, Southeast University, Nanjing 210096

收稿日期: 2020-08-6   修回日期: 2020-09-18  

基金资助: * 国家自然科学基金资助项目.  51477028

Received: 2020-08-6   Revised: 2020-09-18  

作者简介 About authors

许翰宸,男,1998年生。主要研究方向为电力测量、电气工程及其自动化。E-mail： 1025240855@qq.com

王立辉,男,1979年生,教授,博士研究生导师。主要研究方向为电气设备巡检,机器视觉、深度学习等。E-mail： lyh7277363@163.com

廖宇航,男,1996年生。主要研究方向为电力测量、电气工程及其自动化。E-mail： 995882901@qq.com

摘要

分布式发电(Distributed generation, DG)单元高渗透性会造成各种电能质量问题,从而导致电网承载能力降低。为此,提出一种面向分布式电源的改进灰狼优化与引力搜索(Grey wolf optimization and gravity search,GWO-GS)电网承载力提升方法。提出一种谐波滤波器,大范围地抑制谐波并降低功率损耗,从而最大限度地提高谐波约束的随机性承载能力。利用控制系数的自适应调节和适应度值对权重的作用,同时采用改进灰狼算法进行优化,避免陷入局部最优。结合DG间歇输出功率、负载变化等不确定因素,构建基于改进GWO-GS的滤波器优化。利用Matlab仿真平台对所提优化算法进行验证,结果表明所提算法的收敛时间最短,性能优于其他算法。

关键词： 分布式发电 ; 改进灰狼优化 ; 引力搜索 ; 承载能力 ; 谐波滤波器

Abstract

The high permeability of distributed generation (DG) units will cause various power quality problems, which will lead to the reduction of power grid carrying capacity. Therefore, a method to improve the load-carrying capacity of DG connected to power grid based on improved grey wolf optimization and gravity search (GWO-GS) is proposed. Firstly, a harmonic filter is proposed to suppress harmonics and reduce power loss, so as to maximize the random carrying capacity of harmonic constraints. Then, the adaptive adjustment of control coefficient and the effect of fitness value on weight are used, and the improved gray wolf algorithm is used to optimize to avoid falling into local optimum. Finally, combined with uncertain factors such as DG intermittent output power and load change, the filter optimization based on improved GWO-GS is constructed. In addition, Matlab simulation platform is used to verify the proposed optimization algorithm. The results show that the proposed algorithm has the shortest convergence time and better performance than other algorithms.

Keywords： Distributed generation ; improved gray wolf optimization ; gravitational search ; hosting capacity ; harmonic filter

PDF (459KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

许翰宸, 王立辉, 廖宇航. 面向分布式电源的改进GWO-GS电网承载力提升方法*. 电气工程学报[J], 2021, 16(2): 141-148 doi:10.11985/2021.02.018

XU Hanchen, WANG Lihui, LIAO Yuhang. Method of Improving Power Grid Hosting Capacity for Distributed Generation Based on Improved GWO-GS. Journal of Electrical Engineering[J], 2021, 16(2): 141-148 doi:10.11985/2021.02.018

1 引言

可再生能源由于其可持续性、生态友好性和技术经济优势,在能源系统中发挥着至关重要的作 用[1]。现如今,许多国家的能源发电结构使用更多的可再生分布式发电(Distributed generation,DG)机组,取代传统的化石燃料资源,以尽量减少排放[2]。然而,由于DG存在随机性和不确定性,过度渗透到电网可能会增加过电压风险、造成电气设备过载和反向功率流,对电网保护和电能质量等问题产生负面影响[3]。

当DG渗透超过电网安全可靠运行的最大允许标准,即系统承载能力极限时,电网极易受到各种风险的影响[4]。因此承载能力分析对于现代网络规划和电力公司来说至关重要。在承载力分析的基础上,致力提升电网的承载能力,以允许更多的DG接入,同时确保电网安全可靠地运行。

目前已有一些用于提升电网承载能力的方法,大致分为六种类型：无功功率控制、有载分接开关变压器电压控制、系统加固和重新配置、储能技术、有功功率削减和谐波抑制技术[5]。其中无功功率控制技术(如并联电容器组、静态无功补偿器和智能逆变器控制的DG单元)克服了DG高渗透所造成的过电压问题,是最有效的承载能力提升方法之一[6]。并且系统的重构和增强也是提升承载能力的有效方法,文献[7]提出了利用最优导线加固框架提升承载能力,并提出了一种新的馈线加固指标FRI,以利用可再生能源重新配置电力系统。此外,储能系统允许负荷需求和发电之间的有效解耦,并且具备电压控制、降低功率损耗等优势,有助于减轻因DG过度接入而产生的过电压,提高系统的承载能力[8]。同时,主动限功率技术也应用于DG高渗透问题,电力公司可以调整DG机组的输出功率,以符合电力系统的运行限制。目前已提出许多限功率技术,如软限功率和硬限功率技术、固定限功率和电压相关的电压/功率控制方法等[9]。

从电能质量的角度分析,一方面,非线性负载的迅速增加对配电系统的电能质量有着显著的影响;另一方面,电网接入分布式发电系统与其电力电子接口的集成,可能导致系统高度失真[10]。为此,专家学者们提出了各种谐波抑制技术,如单调谐波无源滤波器、无源滤波器、有源谐波滤波器等,以提升谐波约束的承载能力[11]。文献[12]中检查了间谐波和超谐波及其对承载能力的影响,但动态框架采用了许多不确定的参数,如天气变化引起DG发电功率的改变等,而网络建模中的不确定性需要在没有确定的实时测量的情况下才能更好地评估承载能力。而确定性承载能力评估方法只能显示电网承载更多DG单元能力的保守估计。

针对确定性承载能力中忽略了各种参数的不确定性以及DG接入的电网承载力较低等问题,提出了一种面向分布式电源的改进灰狼优化与引力搜索(Grey wolf optimization and gravitational search,GWO-GS)电网承载力提升方法,主要创新点总结 如下。

(1) 针对DG高渗透率下电网谐波畸变的功率因数校正问题,提出了一种无源谐波滤波器,大范围地抑制谐波并且降低功率损耗,从而最大限度地提高随机性承载能力。

(2) 针对DG间歇输出功率、负载变化等不确定性因素,提出了一种优化问题,明确了随机性承载能力最大的优化目标和约束条件,全面提升电网对DG接入的承载能力。

(3) 由于单一优化算法的性能不佳,因此提出基于改进GWO-GS混合模型用于滤波器的优化设计。自适应控制系数可避免陷入局部最优,快速实现全局寻优。

2 分布式电源接入电网的系统模型

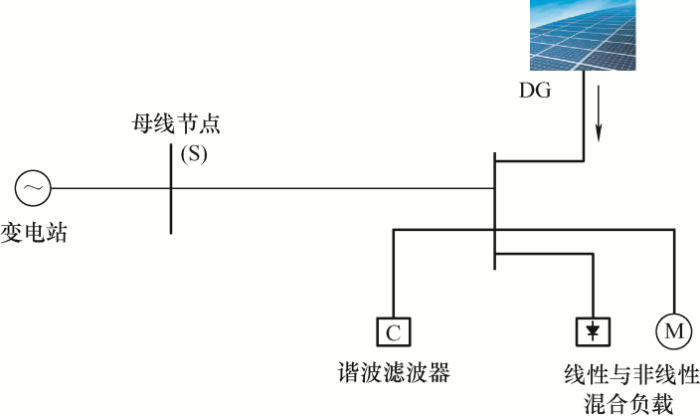
分布式电源接入电网的系统模型如图1所示,该系统由变电站、配电线路、线性负载与非线性负载、DG单元和谐波滤波器构成[13]。在此系统中,可能存在三种谐波,即电力系统原有的电压谐波、光伏系统注入的电流谐波以及由于负载非线性而产生的电流谐波。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   分布式电源接入电网的系统模型


2.1 系统理论模型

由于系统中各个模型的不确定性,通常采用概率分布,如正态概率密度函数(Probability density function,PDF)表示该不确定参数的变化。其标准PDF$T(x)$由期望平均值$\mu $和标准偏差σ表示

$T(x)=\frac{1}{\sigma \times 2\text{ }\!\!\pi\!\!\text{ }}\exp \left[ \frac{-{{(x-\mu)}^{2}}}{2{{\sigma }^{2}}} \right]$

且随机变量$x$存在于其极限内的98%置信水平(Confidence level,CL)的期望平均值如下

${{\mu }^{\text{98}}}=\frac{({{x}_{\max }}-{{x}_{\min }})/2}{1.96}$

式中,${{x}_{\max }}和{{x}_{\min }}$分别为$x$的最大值和最小值。

系统理论模型包括：① 线性模型,对于谐波潮流计算,馈线或线路用其谐波导纳表示;② 负荷模型,混合负荷一般由线性负荷和非线性负荷组成。其中典型的线性负载包括照明、热负载等,用等效导纳进行运算,而非线性负载模型通常由注入相应谐波电流的电流源构建,其基波电流可通过基波潮流获得;③ 光伏系统模型,从谐波潮流的角度分析,以光伏系统为代表的DG电源通常被视为谐波电流源;④ 谐波滤波器模型,所提出的谐波滤波器是一种高通无源滤波器。

谐波滤波器作为基波并联电容器组,能保证对大范围谐波进行适当的谐波抑制,消除谐振风险,且功率损耗非常低。该滤波器由一个主电容器CF1组成,且主电容器与电感器LF、辅助电容器CF2和电阻RF的双臂组合串联。因此,滤波器的谐波阻抗$Z_{F}^{h}$可以视为主电容器阻抗${{Z}_{CF1}}$和双臂支路阻抗${{Z}_{db}}$的等效阻抗,计算如下

$Z_{F}^{h}={{Z}_{CF1}}+{{Z}_{db}}=-j\left( \frac{{{X}_{CF1}}}{h} \right)+\left( \frac{j{{R}_{F}}h\times ({{h}^{2}}-1)}{h{{R}_{F}}+j{{X}_{F}}({{h}^{2}}-1)} \right)$

式中,${{X}_{CF1}}$、${{X}_{F}}$分别为主电容器和电感器的电抗值,${{R}_{F}}$为电阻值,$h$为支路数。

2.2 系统优化目标

首先求解系统的基波潮流,得到系统的基波电压和基波电流,然后分析系统谐波潮流,以找出系统的非基波谐波电压和电流。获得的高次谐波线路电流矢量如下

${{Y}^{h}}\times {{V}^{h}}={{I}^{h}}$

式中,${{V}^{h}}$和${{Y}^{h}}$分别为高次谐波的谐波电压和导纳矩阵。

所提出系统的优化问题在于使系统的随机性承载能力最大化,使电网最大程度地承载分布式电源。

2.2.1 目标函数

所提优化问题的目标函数是使系统的随机性承载能力最大化,即

$\text{max}PH{{C}^{\text{98}}}=PH{{C}^{\text{98}}}(X_{CF1}^{98},X_{F}^{98},R_{F}^{98},P_{PV}^{98})$

式中,$PH{{C}^{\text{98}}}$为随机性承载能力(Probabilistic hosting capacity,PHC)的98%,$X_{CF1}^{98}、X_{F}^{98}、R_{F}^{98}和P_{PV}^{98}$分别为滤波器主电容电抗、滤波器基波等效电抗、滤波器阻尼电阻的98%和光伏系统注入有功功率的98%。

2.2.2 约束条件

由于网络参数具有概率性,因此应选择相关约束条件以考虑该参数的不确定性。所提方法考虑以下四个约束条件。

(1) 母线电压限制。母线电压$U_{m}^{98}$应保持在其规定的最小和最大限度内,即

$U_{m}^{\min }\le U_{m}^{\text{98}}\le U_{m}^{\max }$

式中,$U_{m}^{\min }和U_{m}^{\max }$分别为最小和最大母线电压,其最小和最大母线电压分别限制为0.95 V和1.05 V。

(2) 线路容量限制。线电流$I_{L}^{\text{98}}$受其最大热容量$I_{L}^{\max }$的限制,即

$I_{L}^{\text{98}}\le I_{L}^{\max }$

(3) DG容量限制。DG机组产生的总有功功率的98%受总连接负载容量的限制,以避免过多的反向功率流。

(4) 谐波失真约束。在电网存在多个电流和电压谐波畸变源的情况下,应考虑具体的约束条件,避免因谐波畸变过大而造成运行危害[14]。其中,主要的谐波畸变包括总需求失真(Total demand distortion,TDD)$TD{{D}^{98}}$和电压总谐波失真(Total harmonic distortion of voltage,THDV)$THDV_{h}^{98}$计算如下

$\left\{ \begin{align} & TD{{D}^{98}}={\sqrt{\sum\limits_{h>1}{{{\left| I_{L}^{98} \right|}^{2}}}}}/{{{I}_{f1}}}\;\le TD{{D}_{\max }} \\ & THDV_{h}^{98}(\%)={\left| V_{L}^{98} \right|}/{V_{L}^{1}}\;\times 100\le THDV_{\max }^{h} \\ \end{align} \right.$

式中,$TD{{D}^{\max }}$和$THDV_{\max }^{h}$分别为$TD{{D}^{98}}$和$THDV_{h}^{98}$的最大允许限值,${{I}_{f1}}$为正常运行条件下的满载电流,$V_{L}^{1}$为基本线路母线电压。

3 基于改进GWO-GS混合模型的电网承载力提升方法

近年来,大量的元启发式优化算法被提出,如粒子群算法、差分进化算法、遗传算法、蚁群算法、引力搜索算法等,其目的是从所有已实现的结果 中以时效的方式获得最佳结果(全局最优)。为了更好地实现全局最优,将若干启发式优化算法进行组合,以利用每种独立技术的优点,提高搜索算法的性能。而所提搜索算法将改进GWO和GS算法 相结合,以克服引力搜索算法易陷入局部最优的不足,发挥两种算法的优势,以最快的速度获得最优解。根据所提算法得到的优化结果,即分布式电源接入电网的功率最大且系统谐波在允许的范围内,控制无源谐波滤波器的工作状态。

3.1 自适应权重调节改进GWO算法

GWO算法的寻优过程是模拟灰狼群的社会等级制度和捕食策略。灰狼等级群体内依次分成$\alpha 、\beta 、\gamma 、\varsigma $四个等级且逐渐降低,狼群捕食的过程就是寻优过程,猎物的位置为最优解[15]。

假定灰狼总数是$N$,维度是$e$,则狼群可表示为$X=\left( {{X}_{1}},{{X}_{2}},\cdots,{{X}_{N}} \right)$,第$i$只灰狼在第$e$维度上表示为${{X}_{i}}=\left( X_{i}^{1},X_{i}^{2},\cdots,X_{i}^{e} \right)$。在移动过程中,猎物的位置随机,因此灰狼的位置更新由$\alpha \beta \gamma $狼主导,位置更新如下

$\left\{ \begin{align} & {{X}_{1}}(t+1)={{X}_{\alpha }}(t)-{{A}_{1}}\cdot \left| {{C}_{1}}\cdot {{X}_{\alpha }}(t)-X(t) \right| \\ & {{X}_{2}}(t+1)={{X}_{\beta }}(t)-{{A}_{2}}\cdot \left| {{C}_{2}}\cdot {{X}_{\beta }}(t)-X(t) \right| \\ & {{X}_{3}}(t+1)={{X}_{\gamma }}(t)-{{A}_{3}}\cdot \left| {{C}_{3}}\cdot {{X}_{\gamma }}(t)-X(t) \right| \\ \end{align} \right. \\ X(t+1)=\frac{{{X}_{1}}(t+1)+{{X}_{2}}(t+1)+{{X}_{3}}(t+1)}{3} \\ A=\text{2}a{{r}_{2}}-a\ \ \ \ C=\left| C\cdot {{X}_{w}}(t)-X(t) \right| $

式中,$t$为当前迭代次数,${{X}_{w}}(t)$为第$t$次搜索后的最优灰狼位置,${{r}_{1}},{{r}_{2}}$为[0,1]间的随机矢量,$C$为权重系数,$a=2(1-t/{{t}_{\max }})$为调节系数,其中${{t}_{\max }}$为最大迭代次数。每次位置更新后,根据适应度值选择新的$\alpha \beta \gamma $,进入下一次迭代,直至迭代结束,获得最优解。

由于基本GWO算法对$\alpha \beta \gamma $的关键性没有明显区别,针对此不足,采用适应度值替代位置值动态调整权重为

$X(t+1)=\frac{{{\mu }_{\text{1}}}{{X}_{1}}(t)+{{\mu }_{\text{2}}}{{X}_{2}}(t)+{{\mu }_{\text{3}}}{{X}_{3}}(t)}{3}$

式中,${{\mu }_{1}}=\frac{\left| {{Q}_{1}} \right|}{\left| {{Q}_{1}} \right|+\left| {{Q}_{2}} \right|+\left| {{Q}_{3}} \right|}$,其中$Q$为每只灰狼的适应度值。

此外,调节系数$a$是线性递减的,易陷入局部最优。为此,所提算法中采用$\alpha \beta \gamma $狼的平均适应度值相对于上一时刻的变化率对参数$a$进行自适应调节,当其变化率小时加快局部搜索,当变化率大时减缓全局搜索。则$a$自适应调节为

$a={{a}_{\max }}-({{a}_{\max }}-{{a}_{\min }}){{(t/{{t}_{\max }})}^{2}}\exp (-k)$

式中,$k=\frac{\bar{Q}(t+1)-\bar{Q}(t)}{\bar{Q}(t)}$,$\bar{Q}$为$t$时刻$\alpha \beta \gamma $适应度值的平均值,${{a}_{\max }}$、${{a}_{\min }}$分别为调节系数的最大值和最小值。

3.2 GS算法优化DG接入方式

GS算法遵循牛顿万有引力定律,不同质量的个体在解空间中相互吸引,个体间通过引力的作用朝着质量大的个体运动[16]。其由引力$F$和个体运动的加速度$a$共同表述。

在一个$e$维的搜索空间中,假设DG接入个体总数为$N$,在$t$时刻,第$j$个个体作用在第$i$个个体上的引力$F_{ij}^{e}$为

$F_{ij}^{e}(t)=G(t)\frac{{{M}_{pi}}(t)\times {{M}_{aj}}(t)}{{{R}_{ij}}(t)}(x_{j}^{e}(t)-x_{i}^{e}(t))$

式中,${{R}_{ij}}(t)={{\left\| {{X}_{i}}(t),{{X}_{j}}(t) \right\|}_{2}}$,${{M}_{aj}}(t)$、${{M}_{pi}}(t)$分别为作用在个体$j$和$i$的惯性质量,${{X}_{i}}=\left( x_{i}^{1},x_{i}^{2},\cdots,x_{i}^{e},\cdots,x_{i}^{n} \right)\text{ }i=1,2,\cdots,N$为个体位置,$x_{i}^{e}$为第$i$个个体在第$e$维上的位置,$G$为引力系数,$M$为个体的惯性质量,$R$为个体间的距离。

在$t$时刻,个体$i$在第$e$维上的加速度$a_{i}^{e}(t)$ 为[17,18]

$a_{i}^{e}(t)={F_{i}^{e}(t)}/{{{M}_{i}}(t)}\;$

在GS算法中,对于每一次迭代,个体的速度$v_{i}^{e}\left( t+1 \right)$和位置公式$x_{i}^{e}\left( t+1 \right)$更新如下

$v_{i}^{e}(t+1)=ran{{d}_{i}}\times v_{i}^{e}(t)+a_{i}^{e}(t)$
$x_{i}^{e}(t+1)=x_{i}^{e}(t)+v_{i}^{e}(t+1)$

3.3 改进GWO-GS算法用于提升电网承载力

GS算法在解决各种优化问题中具有显著的搜索能力,但该算法仍存在收敛速度慢、易陷入局部极小等缺点,而改进GWO算法通过相关系数自适应调节和权重优化以避免搜索局部最优[19]。因此,所提方法将改进GWO和GS算法结合,获取DG接入电网的最优方式,并控制谐波滤波器的工作状态,以提升电网对分布式电源的承载能力[20]。

改进GWO-GS算法中,搜索DG接入个体速度$v_{t+1}^{j}$和位置$X_{t+1}^{j}$更新如下

$v_{t+1}^{j}={{\kappa }_{1}}\cdot v_{t}^{j}+{{S}_{X}}\cdot {{\kappa }_{2}}\cdot a_{t}^{j}+{{S}_{Y}}\cdot {{\kappa }_{3}}\cdot a_{t}^{j}(Xbest-X_{t}^{j})\text{ }\forall j\in N$
$X_{t+1}^{j}=X_{t}^{j}+v_{t+1}^{j}$

式中,$X_{t}^{j}$、$v_{t}^{j}$和$a_{t}^{j}$分别为第$t$次迭代中第$j$个个体的位置、速度和加速度,${{\kappa }_{\text{1}}}、{{\kappa }_{\text{2}}}和{{\kappa }_{\text{3}}}$为[0,1]范围内均匀分布的随机数,${{S}_{X}}和{{S}_{Y}}$为正系数,$Xbest$为迄今为止最优位置。其中,${{\kappa }_{\text{1}}}、{{\kappa }_{\text{2}}}和{{\kappa }_{\text{3}}}$利用适应度值作为判据动态调整其数值,以凸显每个个体在寻优过程中的重要程度[21,22]。进行系统试验时,群体中的个体总数为500,${{S}_{X}}和{{S}_{Y}}$的取值分别为0.5和1.5,GS的初始量${{G}_{\text{0}}}$为1,搜索代理数量为20[23]。

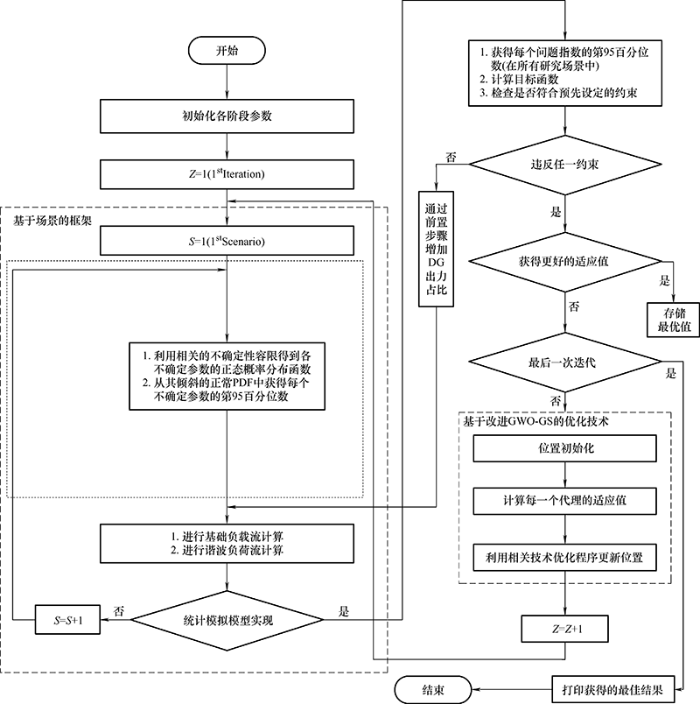
由于优化目标是使滤波器电抗与DG的有功功率最大,因此利用所提算法对滤波器的电抗参数和DG功率参数$X_{CF1}^{98}、X_{F}^{98}、R_{F}^{98}和P_{PV}^{98}$进行寻优,利用获得的最优值设定滤波器以及控制DG的接入量。改进GWO-GS算法用于提升电网对DG承载力的整体执行流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   改进GWO-GS算法整体流程图


首先,获取系统内各种负荷、线路、DG及滤波器的相关数据,并初始化模型的参数。

然后进行统计模拟,在每次统计模拟中,利用相关的不确定性容量得到各不确定参数的正太概率分布函数,并且从其修正的正常PDF中获得每个不确定参数的98%,以此为基础计算系统谐波[24,25]。

最后,根据现行系统的参数(线路谐波导纳、母线电压、支路容量、滤波器谐波电抗和DG功率输出),结合设定的优化目标与约束条件,利用改进GWO-GS算法获得最优的谐波电抗值与DG接入量,从而控制谐波滤波器的工作状态和电网接入DG的功率量,以保证电网的稳定运行[26]。

4 试验分析

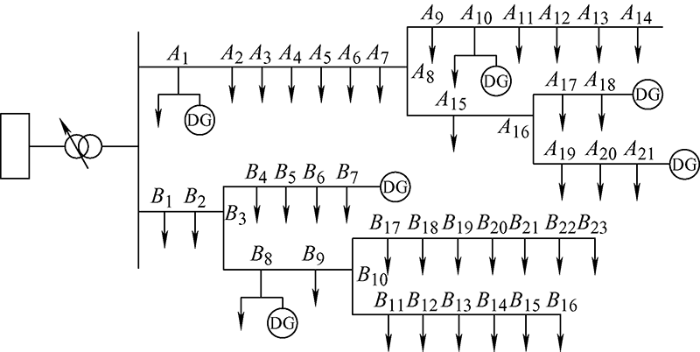
基于Matlab仿真平台对系统进行建模,如图3所示。其基准电压设为10 kV,视在功率为20 MV·A,总负载功率因数为0.92,额定负载有功功率和无功功率需求分别为0.92 p.u.和0.39 p.u.,非线性负载功率与总负载功率之比为30%,其中DG的输出功率存在随机性,假设功率变化范围为0~100 kW,各个节点的负荷功率不一,且时刻变化。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   系统仿真模型


此外,未补偿系统会存在超过标准限值的谐波失真,而且柴油渗透可能会进一步恶化系统的运行指标。为此,采用所提的无源谐波滤波器以缓解谐波失真问题,从而提高系统对分布式电源的承载能力。试验中将所提的改进GWO-GS算法与文献[7]、文献[12]中元启发式优化算法所获得的确定性承载能力和随机性承载能力结果进行比较分析。

4.1 确定性承载能力分析

所提出的谐波滤波器采用改进GWO-GS算法与文献[7]、文献[12]中的算法对其确定性承载能力结果进行比较分析。使用三种优化算法的最优滤波器参数和系统主要运行指标如表1所示。

表1   利用不同滤波器获得的操作参数和确定性承载能力结果

参数基准补偿系统
改进GWO-GS文献[7]文献[12]
Vmin/p.u.0.958 30.935 30.978 50.987 2
TDD(%)6.657 57.868 68.357 28.000 1
THDV(%)5.454 34.042 24.123 34.145 1
滤波器损耗/p.u.0.003 00.003 10.003 40.003 3
总功率损耗/p.u.0.037 50.006 20.007 30.007 5
位移功率因素0.921 30.998 20.953 60.975 2
功率因素91.685 60.986 70.965 20.975 4
确定性承载能力(%)50.0056.5150.7249.18

新窗口打开| 下载CSV


从表1中可看出,使用改进GWO-GS算法的滤波器的性能优于使用文献[7]和文献[12]算法的滤波器,因为所提算法的承载能力和系统电压更高,TDD电平和THDV电平更低,并且提高了功率因素和位移功率因素值。此外,使用改进GWO-GS算法获得的滤波器电阻RF小于其他方法获得的滤波器电阻,因此滤波器损耗更低,从而整体系统的总功率损耗最低。

可以注意到,确定性承载能力评估依赖于系统参数的固定值,但在实际系统中,其参数会发生不确定的变化。因此确定性承载能力明显偏低,需要评估系统中存在的各种不确定性,如DG的间歇输出功率、电压谐波、负载变化以及滤波器参数的变化等。

4.2 随机性承载能力分析

为了进行随机性承载能力分析,利用统计模拟模型生成适当数量不确定参数,其中,每个不确定参数的统计模拟模型迭代次数为1 500。

使用统计模拟模型概率操作指标,即TDD、THDV、位移功率因数、功率因数、方均根母线电压和随机性承载能力。

在随机性承载能力分析中,使用改进GWO-GS算法的滤波器和文献[7]、文献[12]算法滤波器的随机性承载能力指标如表2所示。

表2   使用设计的滤波器获得的操作参数和随机性承载能力结果

参数补偿系统
改进GWO-GS文献[7]文献[12]
Vmin/p.u.0.994 30.988 50.987 2
TDD(%)7.866 67.352 27.203 8
THDV(%)4.432 14.191 34.143 1
滤波器损耗/p.u.0.001 80.002 90.002 3
总功率损耗/p.u.0.003 50.004 10.004 5
位移功率因素0.999 20.972 60.961 4
功率因素0.967 70.945 20.913 4
随机性承载能力(%)74.0570.3869.98

新窗口打开| 下载CSV


从表2可看出,所提算法的随机性承载能力指标更佳。其中,所提算法获得的位移功率因素、功率因素和电压分布都比其他方法高,从而提高了电压水平。此外,使用改进GWO-GS算法获得的滤波器电阻${{R}_{F}}$小于其他方法获得的滤波器电阻,因此滤波器损耗更低,从而整体系统的总功率损耗最低。

4.3 性能对比分析

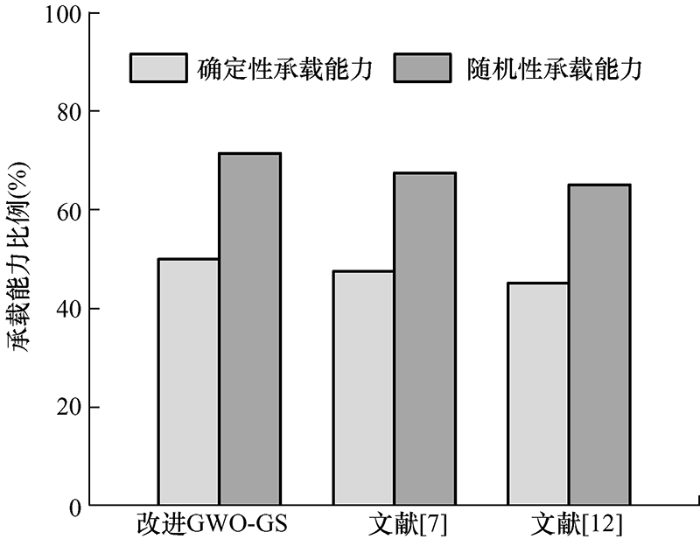
对比分析提出的方法与文献[7]、文献[12]中优化算法实现的确定性承载能力和随机性承载能力结果如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同优化算法的承载能力结果对比


从图4看出,所提算法实现的确定性承载能力和随机性承载能力均比其他文献中实现的承载能力要高,由于所提算法将改进GWO与GS算法相结合,避免了陷入局部最优,且以最快的速度寻得最优解,实现分布式电源的高效接入。此外,随机性承载能力的值普遍比确定性承载能力要高,这是因为确定性承载能力中忽略了参数的可变性。

5 结论

为了提高电网对DG接入的承载能力,本文提出一种谐波滤波器,最大限度地提高系统的随机性承载能力,同时综合考虑DG的间歇输出功率、负载变化等不确定性因素,构建优化目标函数,使用改进GWO-GS优化算法进行问题求解,以最短的时间寻得全局最优解。此外,利用Matlab仿真对所提方法进行了验证,得出如下结论。

(1) 相比于其他方法,所提方法采用GWO算法改进GS算法,能够加快收敛速度,快速寻优。

(2) 由于确定性承载能力忽略参数的不确定性,其低于随机性承载能力,因此所提方法能够很大程度地提升电网的承载力。

但所提方法仅限于固定的、与时间无关的负载曲线和光伏输出功率,以及其对平衡配电系统性能的影响。此外,所提方法不适用于不平衡配电系统,这也是接下来的工作重点。

参考文献

唐程辉, 张凡, 张宁, 等.

考虑可再生能源随机性和需求响应的电力系统日前经济调度

[J]. 电力系统自动化, 2019, 43(15):18-25,26-28,63.

[本文引用: 1]

TANG Chenghui, ZHANG Fan, ZHANG Ning, et al.

Day ahead economic dispatch of power system considering randomness and demand response of renewable energy

[J]. Automation of Electric Power Systems, 2019, 43(15):18-25,26-28,63.

[本文引用: 1]

PASHA A M, ZEINELDIN H H, EL-SAADANY E F, et al.

Optimal allocation of distributed generation for planning master-slave controlled micro-grids

[J]. IET Generation Transmission & Distribution, 2019, 13(16):3704-3712.

DOI:10.1049/gtd2.v13.16      URL     [本文引用: 1]

杨本臣, 苑齐鼎, 刘海权.

计及分布式发电预测的微电网孤岛供电可靠性评估

[J]. 电力系统及其自动化学报, 2019(6):50-54.

[本文引用: 1]

YANG Benchen, YUAN Qiding, LIU Haiquan.

Reliability evaluation of micro-grid island power supply considering distributed generation prediction

[J]. Proceedings of the CSU-EPSA, 2019(6):50-54.

[本文引用: 1]

李健康, 韦笃取, 罗晓曙, 等.

分布式发电系统与感性负载网络混沌同步控制

[J]. 广西师范大学学报, 2019(3):33-41.

[本文引用: 1]

LI Jiankang, WEI Duqu, LUO Xiaoshu, et al.

Chaos synchronization control of distributed generation system and inductive load network

[J]. Journal of Guangxi Normal University, 2019(3):33-41.

[本文引用: 1]

AHMADIPOUR M, HIZAM H, OTHMAN M L, et al.

Islanding detection method using ridgelet probabilistic neural network in distributed generation

[J]. Neurocomputing, 2019, 329:188-209.

DOI:10.1016/j.neucom.2018.10.053      URL     [本文引用: 1]

周礼来, 熊洁, 李稳国, 等.

微电网分布式发电模拟系统的设计

[J]. 湖南城市学院学报, 2019, 28(4):52-56.

[本文引用: 1]

ZHOU Lilai, XIONG Jie, LI Wenguo, et al.

Design of microgrid distributed generation simulation system

[J]. Journal of Hunan City University, 2019, 28(4):52-56.

[本文引用: 1]

MAHROO-BAKHTIARI R, IZADI M, SAFDARIAN A, et al.

Distributed load management scheme to increase PV hosting capacity in LV feeders

[J]. IET Renewable Power Generation, 2019, 14(1):125-133.

DOI:10.1049/rpg2.v14.1      URL     [本文引用: 8]

XU X, LI J, XU Z, et al.

Enhancing photovoltaic hosting capacity:A stochastic approach to optimal planning of static var compensator devices in distribution networks

[J]. Applied Energy, 2019, 238:952-962.

DOI:10.1016/j.apenergy.2019.01.135      URL     [本文引用: 1]

刘洪, 徐正阳, 葛少云, 等.

考虑储能调节的主动配电网有功-无功协调运行与电压控制

[J]. 电力系统自动化, 2019, 43(11):51-62.

[本文引用: 1]

LIU Hong, XU Zhengyang, GE Shaoyun, et al.

Active reactive coordinated operation and voltage control of active distribution network considering energy storage regulation

[J]. Automation of Electric Power Systems, 2019, 43(11):51-62.

[本文引用: 1]

常栋梁, 何立柱, 李洋, 等.

配电网功率平衡调节与无功补偿研究及装置

[J]. 电力系统及其自动化学报, 2019(4):132-138.

[本文引用: 1]

CHANG Dongliang, HE Lizhu, LI Yang, et al.

Research and device of power balance regulation and reactive power compensation in distribution network

[J]. Proceedings of the CSU-EPSA, 2019(4):132-138.

[本文引用: 1]

朱瑞金, 郭威麟, 龚雪娇.

基于自编码器和卷积神经网络的电能质量扰动分类

[J]. 电力系统及其自动化学报, 2019, 31(7):70-75.

[本文引用: 1]

ZHU Ruijin, GUO Weilin, GONG Xuejiao.

Power quality disturbance classification based on self encoder and convolutional neural network

[J]. Proceedings of the CSU-EPSA, 2019, 31(7):70-75.

[本文引用: 1]

ISMAEL S M, ALEEM S H E A, ABDELAZIZ A Y, et al.

State-of-the-art of hosting capacity in modern power systems with distributed generation

[J]. Renewable Energy, 2019, 130:1002-1020.

DOI:10.1016/j.renene.2018.07.008      URL     [本文引用: 8]

KRISTOV L.

The bottom-up (R) evolution of the electric power system:The pathway to the integrated- decentralized system

[J]. IEEE Power and Energy Magazine, 2019, 17(2):42-49.

DOI:10.1109/MPE.2018.2885204      URL     [本文引用: 1]

叶学顺, 何开元, 刘科研.

有源配电网重构与多级无功联动优化

[J]. 电力系统保护与控制, 2019, 47(13):115-123.

[本文引用: 1]

YE Xueshun, HE Kaiyuan, LIU Keyan.

Active distribution network reconfiguration and multi-level reactive power linkage optimization

[J]. Power System Protection and Control, 2019, 47(13):115-123.

[本文引用: 1]

LAKUM A, MAHAJAN V.

Optimal placement and sizing of multiple active power filters in radial distribution system using grey wolf optimizer in presence of nonlinear distributed generation

[J]. Electric Power Systems Research, 2019, 173:281-290.

DOI:10.1016/j.epsr.2019.04.001      URL     [本文引用: 1]

TEFEK M F, UĞUZ H, GÜÇYETMEZ M.

A new hybrid gravitational search-teaching-learning-based optimization method for energy demand estimation of Turkey

[J]. Neural Computing and Applications, 2019, 31(7):2939-2954.

DOI:10.1007/s00521-017-3244-9      URL     [本文引用: 1]

高飞, 方海莲.

基于引力搜索算法的分数阶变异时序回归GSA-TSGM(1,1)模型

[J]. 计算机应用研究, 2019(6):1668-1672.

[本文引用: 1]

GAO Fei, FANG Hailian.

Fractional mutation time series regression GSA-TSGM(1,1) model based on gravitational search algorithm

[J]. Application Research of Computers, 2019(6):1668-1672.

[本文引用: 1]

MOHANTY P, SAHU R K, PANDA S.

A novel hybrid many optimizing liaisons gravitational search algorithm approach for AGC of power systems

[J]. Automatika, 2020, 61(1):158-178.

DOI:10.1080/00051144.2019.1694743      URL     [本文引用: 1]

谭笑, 王主丁, 李强, 等.

计及多约束的多分布式电源接入配电网最大承载力分段算法

[J]. 电力系统自动化, 2020, 44(4):72-80.

[本文引用: 1]

TAN Xiao, WANG Zhuding, LI Qiang, et al.

Segmentation algorithm for maximum hosting capacity of distributed generator accessing to distribution network considering multiple constraints

[J]. Automation of Electric Power Systems, 2020, 44(4):72-80.

[本文引用: 1]

叶莘, 韦钢, 周利骏, 等.

含分布式电源配电网供电能力的概率评估

[J]. 电力系统及其自动化学报, 2019, 31(4):99-105.

[本文引用: 1]

YE Xin, WEI Gang, ZHOU Lijun, et al.

Probabilistic evaluation on power supply capability of distribution system with distributed generations

[J]. Proceedings of the CSU-EPSA, 2019, 31(4):99-105.

[本文引用: 1]

ALKANO D, SCHERPEN J M A.

Distributed supply coordination for power-to-gas facilities embedded in energy grids

[J]. IEEE Transactions on Smart Grid, 2018, 9(2):1012-1022.

DOI:10.1109/TSG.2016.2574568      URL     [本文引用: 1]

孙瑞松.

基于RT-LAB的微电网运行控制硬件在环仿真

[J]. 电气工程学报, 2019, 14(4):95-102.

[本文引用: 1]

SUN Ruisong.

Hardware in the loop simulation on the operation control of microgrid based on RT-LAB

[J]. Journal of Electrical Engineering, 2019, 14(4):95-102.

[本文引用: 1]

TONG Q, QI J, WANG Y, et al.

Power cable ampacity and influential factors analysis under operation

[J]. Journal of Information Processing Systems, 2018, 14(5):1136-1149.

[本文引用: 1]

张敬安, 王雷涛, 王鹏.

交直流混合配电网电能质量综合检测和补偿方法

[J]. 电气工程学报, 2018, 13(9):38-43.

[本文引用: 1]

ZHANG Jingan, WANG Leitao, WANG Peng.

Power quality detection and compensation method of AC/DC hybrid distribution network

[J]. Journal of Electrical Engineering, 2018, 13(9):38-43.

[本文引用: 1]

HE Y X, JIAO J, CHEN R J, et al.

The optimization of Chinese power grid investment based on transmission and distribution tariff policy:A system dynamics approach

[J]. Energy Policy, 2018, 113(6):112-122.

DOI:10.1016/j.enpol.2017.10.062      URL     [本文引用: 1]

卢志刚, 王文涛, 张丹, 等.

基于配电网可靠性的分布式电源与充换电站协同规划

[J]. 太阳能学报, 2020, 41(4):354-362.

[本文引用: 1]

LU Zhigang, WANG Wentao, ZHANG Dan, et al.

DG and EVCS collaborative planning based on distribution network reliability

[J]. Acta Solar Energy, 2020, 41(4):354-362.

[本文引用: 1]

/

〈 〉