移相全桥变换器(Phase-shifted full bridge,PSFB)以其开关管电压应力低、电气隔离易实现、结构简单等特点广泛应用在中小砖型DC/DC模块中。通过原边谐振电感(包括变压器漏感)与开关管结电容的谐振,可以实现原边开关管零电压开通,通过简单的拓扑结构并采用移相控制方式就可以完成高效率、高功率密度的DC/DC能量变换。同时,副边结合双电感的倍流整流方式,双电感电流纹波对消,电流均分,输出频率翻倍,使得输出电压纹波减少,滤波器体积变小,且在一定程度上也使得线阻减小,更好地实现热功率的分布,有利于效率的提高^{[1,2,3,4,5,6]}。

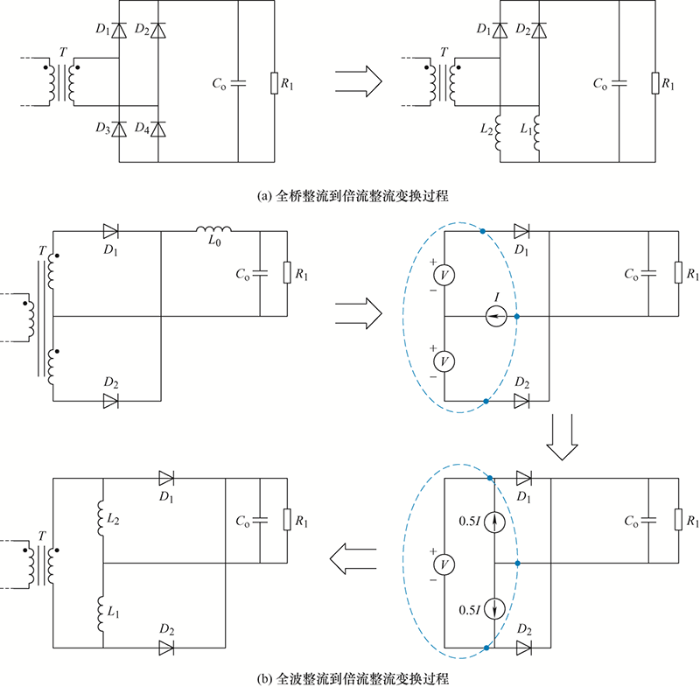
针对中小功率移相全桥变换器,副边主要有两种整流方式：全桥整流与全波整流。在全桥整流中的两组桥臂替换一组上管或下管为电感,即得到新的倍流整流结构,如图1a所示;在全波整流中进行星形到三角形等效替换,也可得到新的倍流整流结构,如图1b所示。相比于传统的两种整流方式,倍流整流每次只有一个二极管导通,且输出电感只分担一半的输出电流,但其电压增益只有全桥整流和中心抽头结构的一半,故更加适合低压大电流环境^[7]。同时本变换器将二极管替换为开关管,采用同步控制策略,避免整流管导通压降带来的损耗^[8]。

由于本文所提出的PSFB-CDSR变换器采用高频变压器实现输入输出端口的隔离,其电感电流是一个纯粹的交流量,不满足平均建模方法所需的小纹波假设^[9],所以根据系统状态变量在相邻采样点之间的转移函数,得到离散迭代模型^[10],其中考虑到变换器的一个周期内的主要子模态,具有较高的精度。文献[11,12,13]中采用该方法对DAB变换器进行研究。文献[14,15]介绍了PSFB的基于PWM开关的小信号分析,其中获得了变换器交流模型作为PWM降压变换器的等效模型,这种方法是基于输入电压和滤波电感电流变化而导致占空比调制的简化分析,但是该模型没有考虑转换器损耗的影响,因而没有考虑转换器效率,最终得到的是基于几个理想假设的一个相对简单的PSFB转换器小信号模型。

文献[16]对PSFB变换器进行进一步的小信号分析,所提出的小信号分析采用基于离散数据采样的非常规平均方法。但是生成的动态模型是非常复杂的,不能通用。相较于以前的简单模型,使用此方法没有讨论该模型的其他优点,而且寄生参数的影响也被忽略了。近年来,引入了基波分析来对PSFB进行分析,例如文献[17]侧重通过基波分析法,引入变压器电压作为中间变量进行傅里叶分解,从而间接得到推导出控制-输出传递函数模型,但是其中只保留了基波和一次谐波,会带来较大误差。

本文在离散时间域建立起PSFB-CDSR变换器的迭代模型,相较于传统电路模型,未使用小信号假设,也避免了模型降阶,完整地保留了全部的电路特征,同时考虑谐振电感回路上的寄生电阻对于系统稳定性的影响,得到考虑损耗的系统稳定条件,更加真实地反映电路的工作状态,从而准确地判断控制系统参数设计的可行性。最后通过仿真,验证了本文离散迭代模型的正确性。

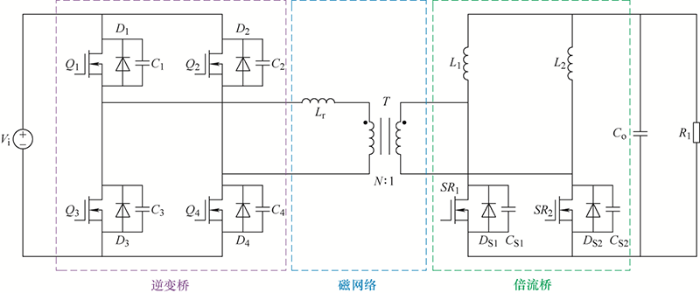
图2为本文提出的移相控制全桥与副边倍流同步整流相结合的拓扑。电路主要有三个单元组成：第一部分为逆变桥部分,包括开关管Q₁~Q₄以及各个上面集成的体二极管D₁~D₄与结电容C₁~C₄;第二部分为磁网络部分,包括变压器T和谐振电感L_r(包含变压器的漏感);第三部分为倍流桥部分,两组桥臂分别由滤波电感L₁、L₂与整流下管SR₁、SR₂组成,并最终与滤波电容C_o和负载R_l相并联。

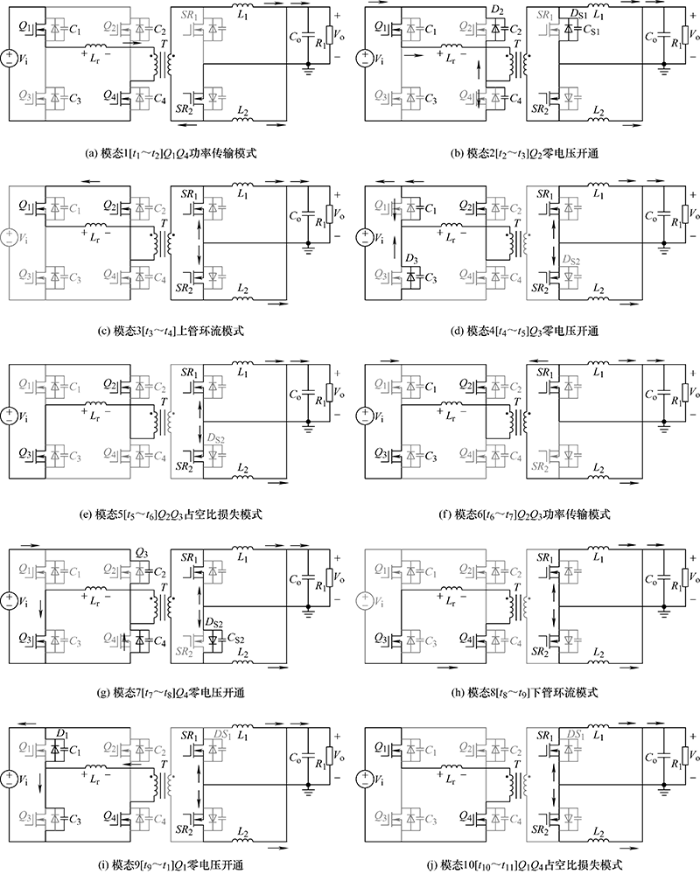
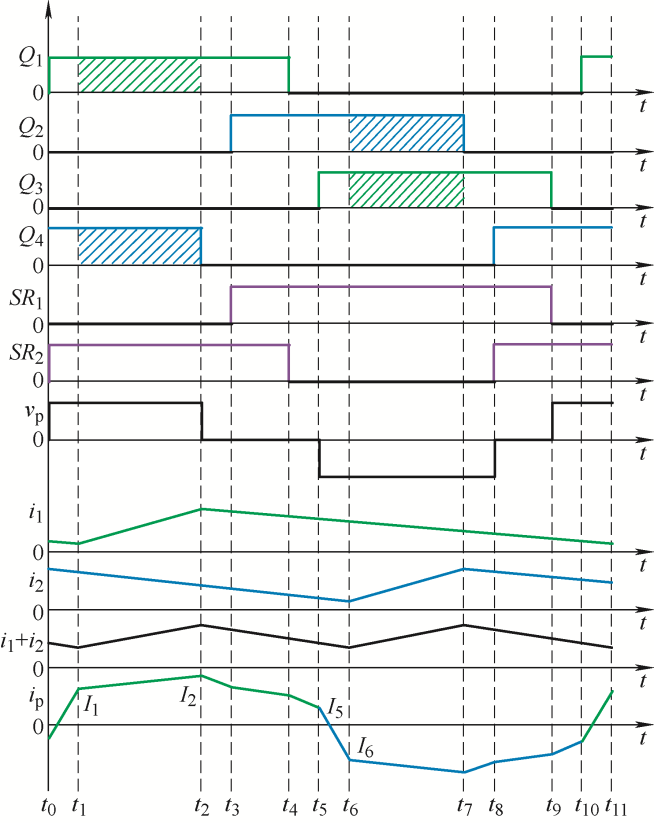
分析假设电路工作在连续导通工作模式(Continuous conduction mode,CCM),且输出电感L₁、L₂和输出电容C_o足够大,可近似考虑成2个电流源和1个电压源。开关管均为理想元件,其结电容取标称值的4/3,且视为不变^[18],其他寄生参数的影响不予考虑。文中假设的变压器励磁电感足够大,故在分析中可以省略励磁电流的影响,谐振电感L_r包括了变压器的漏感与外加电感^[19,20]。设定每组桥臂上下管的驱动信号为互补方式(之间设置有4%的死区),固定占空比D均为48%,上管先于下管导通,于是可定义两组桥臂上管之间的导通时差即为两桥臂的移相角θ,其取值范围在0~D之间。副边倍流桥的同步整流SR₁的驱动信号与Q₂同时开启,与Q₃同时关断,同样地,整流管SR₂的驱动信号也表现为与Q₁和Q₄的逻辑或关系。为深入分析该变换器详细的CCM模式运行情况,将PSFB-CDSR变换器主要划分为10个模态,如图3所示,部分关键的时序波形如图4所示,具体分析如下。

(1) 模态1[t₁~t₂]：如图3a所示,输入电压V_i通过MOS管Q₁与Q₄进行功率传输,对谐振电感L_r充电,并通过变压器将能量传输到副边。对于负载电阻R_l来说,副边侧由两条回路对其供电。通过T-L₁-R_l-SR₂回路,输出滤波电感电流i₁线性增大;通过L₂-R_l-SR₂,输出滤波电感电流i₂缓慢递减,两者电流叠加,即为输出电流。

(2) 模态2[t₂~t₃]：如图3b所示,L_r、C₄、C₂与原边等效串联电感(即副边滤波电感反射到原边的等效值N²L₁)发生滞后桥臂谐振,给C₂放电的同时给C₄充电,直到C₄上电压等于输入电压,两者能量交换完成,Q₂的体二极管导通,此时开通Q₂,即实现了ZVS开通。同时由于原边变压器两端电压降为0,相当于短路,副边滤波电感L₁开始放电,同步整流管SR₁上结电容C_S1也跟随进行放电。

(3) 模态3[t₃~t₄]：如图3c所示,在t₃时刻Q₃两端电压已为0,i_p经由Q₁-L_r-T-Q₂回路进行自由环流,实际中由于线路中存在一定寄生电阻,电流缓慢衰减,原边变压器两端电压在此阶段被钳位至0,相当于短路。副边两同步整流管同时导通,由L₁和L₂放电为负载提供能量。

(4) 模态4[t₄~t₅]：如图3d所示,在t₃时刻Q₁关断,结电容C₁、C₃与电感L_r发生滞后桥臂谐振,C₃在谐振中放电,C₁在谐振中被充电,副边L₁通过SR₁进行放电,SR₂在t₄时刻已关断,L₂通过SR₂ 的体二极管D_S2放电,两电感继续为负载提供能量,不参与此谐振过程。

(5) 模态5[t₅~t₆]：如图3e所示,因为副边L₁和L₂仍处于放电续流阶段,原边变压器仍相当于短路,因为谐振电感L_r上的电流不能突变,在输入电源V_i的作用下,电感电流i_r(变压器原边电流i_p)完成过零变负的整个过程,过零前为能量回馈过程,过零后为谐振电感充电过程。

至此,PSFB-CDSR变换器已完成前半个周期运行,后半周期变压器原边电流反向,向副边传输能量,L₂充能,L₁并联在负载两侧放电,之后进行下管环流,副边双电感释放能量,对负载供电,完成与前五个模态相似的过程,在此不再赘述。

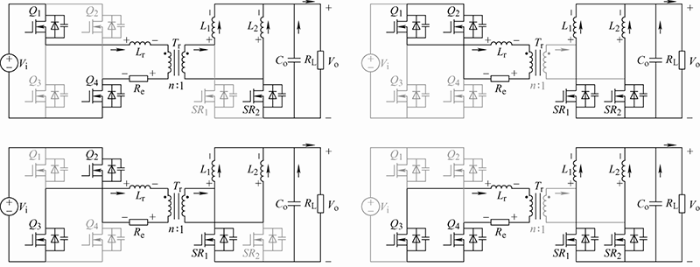
根据以上分析可以将PSFB-CDSR变换器单周期内的十个模态进行化简,按照时间上的占比可以将零电压开通阶段发生的模态省略,具体精简为为四个主要模态,如图5所示,然后根据统一状态方程的描述公式

式中,$x={{\left[ \begin{matrix} \begin{matrix} \begin{matrix} {{i}_{\text{r}}}(t) & {{i}_{\text{1}}}(t) \\ \end{matrix} & {{i}_{2}}(t) \\ \end{matrix} & {{v}_{\text{o}}}(t) \\ \end{matrix} \right]}^{\text{T}}}$表示系统的状态变量,选择流经谐振电感L_r的电流i_r(t)、流经滤波电流L₁上的电流i₁(t)、流经滤波电感L₂上的电流i₂(t)以及输出滤波电容上的电压v_o(t);下标k表示对应的第k个子状态。考虑到变换器原边存在环流情况存在,本文假设变压器原边侧的回路上等效寄生电阻的存在,对应化简的四个子状态,系统的状态矩阵A_k和输入矩阵B_k为

${{A}_{1}}=\left[ \begin{matrix} \frac{-R}{{{L}_{\text{r}}}+L} & 0 & 0 & \frac{-N}{{{L}_{\text{r}}}+L} \\ \frac{-N{{R}_{\text{e}}}}{{{L}_{\text{r}}}+L} & 0 & 0 & \frac{-{{N}^{2}}}{{{L}_{\text{r}}}+L} \\ 0 & 0 & 0 & \frac{-1}{L} \\ \frac{-N}{{{C}_{\text{o}}}} & 0 & \frac{-1}{{{C}_{\text{o}}}} & \frac{-1}{{{C}_{\text{o}}}{{R}_{\text{L}}}} \\\end{matrix} \right]\ \ \ \ \ \ {{B}_{1}}=\left[ \begin{matrix} \frac{1}{{{L}_{\text{r}}}+L} \\ \frac{N}{{{L}_{\text{r}}}+L} \\ 0 \\ 0 \\ \end{matrix} \right]\text{ }{{A}_{2}}=\left[ \begin{matrix} \frac{-{{R}_{\text{e}}}}{{{L}_{\text{r}}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{-1}{L} \\ 0 & 0 & 0 & \frac{-1}{L} \\ 0 & \frac{-1}{{{C}_{\text{o}}}} & \frac{-1}{{{C}_{\text{o}}}} & \frac{1}{{{C}_{\text{o}}}{{R}_{\text{L}}}} \\\end{matrix} \right]\ \ \ \ \ {{B}_{2}}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ \end{matrix} \right]$

${{A}_{3}}=\left[ \begin{matrix} \frac{-{{R}_{\text{e}}}}{{{L}_{\text{r}}}-L} & 0 & 0 & \frac{-N}{{{L}_{\text{r}}}-L} \\ 0 & 0 & 0 & \frac{-1}{L} \\ \frac{N{{R}_{\text{e}}}}{{{L}_{\text{r}}}-L} & 0 & 0 & \frac{{{N}^{2}}}{{{L}_{\text{r}}}-L} \\ \frac{-N}{{{C}_{\text{o}}}} & 0 & \frac{-1}{{{C}_{\text{o}}}} & \frac{-1}{{{C}_{\text{o}}}{{R}_{\text{L}}}} \\ \end{matrix} \right]\ \ \ \ \ \ {{B}_{3}}=\left[ \begin{matrix} \frac{-1}{{{L}_{\text{r}}}-L} \\ 0 \\ \frac{N}{{{L}_{\text{r}}}-L} \\ 0 \\ \end{matrix} \right]\text{ }{{A}_{4}}=\left[ \begin{matrix} \frac{-{{R}_{\text{e}}}}{{{L}_{\text{r}}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{-1}{L} \\ 0 & 0 & 0 & \frac{-1}{L} \\ 0 & \frac{-1}{{{C}_{\text{o}}}} & \frac{-1}{{{C}_{\text{o}}}} & \frac{1}{{{C}_{\text{o}}}{{R}_{\text{L}}}} \\\end{matrix} \right]\ \ \ \ \ \ \ \ {{B}_{4}}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ \end{matrix} \right]\text{ }$

式中,R_e为原边侧等效寄生电容,R_l表示为负载电阻,L为倍流桥上两电感的值,即L=L₁=L₂,N为变压器的变比。

由于DSP基本实现以PWM方式触发ADC采样处理,所以本文设置的采样点在每个子周期开始时刻,以此可以求得系统在相邻采样点之间转移函数的方式建立起的离散迭代模型。通过对每一个子状态的状态方程进行积分并逐一对四个子状态进行迭代^[10,15-17]。可以得到这种情况下两个相邻采样点之间状态变量的转移函数为

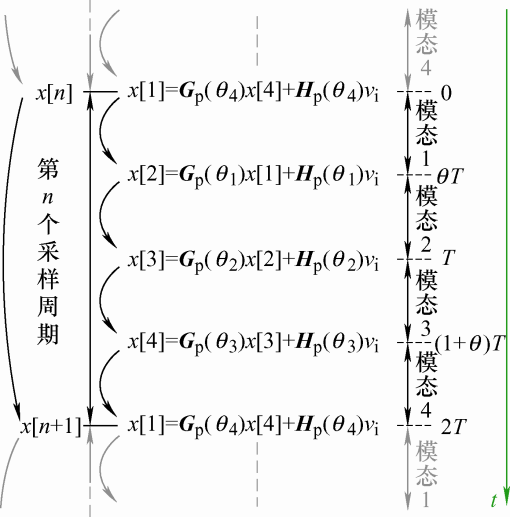
式中,转移函数中的状态矩阵G_p和输入矩阵H_p的求取方法一般分为Z变换法与递推法,但是Z变换法只能适用于线性定常离散系统,本文采取递推法进行求解^[21],其过程如图6所示,由四个子模态转移函数的迭代关系,最终得到相邻两个采样周期x[n]与x[n+1]的转态转移函数,其中,转移函数中的状态矩阵G_p和输入矩阵H_p分别表示为

$\left\{ \begin{align} & {{G}_{\text{p}}}(\theta)=\exp({{A}_{1}}\theta T)\exp({{A}_{2}}(1-\theta)T)\exp({{A}_{3}}\theta T)\exp({{A}_{4}}(1-\theta)T) \\ & {{H}_{\text{p}}}(\theta)=\exp({{A}_{1}}\theta T)\exp({{A}_{2}}(1-\theta)T)\exp({{A}_{3}}\theta T)\int_{0}^{(1-\theta)T}{{}} \\ & \exp({{A}_{4}}t)dt{{B}_{4}}+\exp({{A}_{1}}\theta T)\exp({{A}_{2}}(1-\theta)T)\int_{0}^{\theta T}{\exp({{A}_{3}}\theta T)dt{{B}_{3}}+} \\ & \exp({{A}_{1}}\theta T)\int_{0}^{(1-\theta)T}{\exp({{A}_{2}}t)dt{{B}_{2}}+\int_{0}^{\theta T}{\exp({{A}_{1}}t)dt{{B}_{1}}}} \\ \end{align} \right.$

为了调节输出电压或控制传输功率,必须使变换器工作在稳定状态,闭环系统的稳定性受到变换器硬件参数、端口电压、负载和控制器增益等系统多方面的影响。其中,控制器的参数对整个系统的动态性能和稳定性有巨大影响。如果参数设计不当,则闭环系统会出现明显的振荡现象,显著增大原器件的电压、电流应力,并导致损耗增加或器件损坏,严重影响变换器的正常运行。

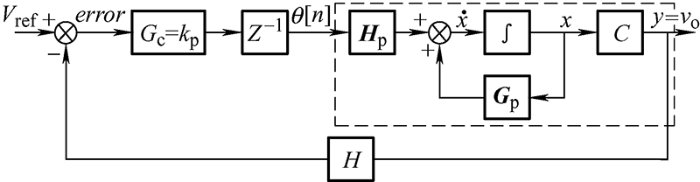
本节对电压闭环控制的PSFB-CDSR变换器系统展开讨论,并应用如图7所示经典的环路系统,以输出电压作为参考,校正系统设置为比例控制器,且考虑到了数字控制器的一拍延时现象^[22]。将系统的输入电压考虑为常量,通过多维空间坐标轴的变换,可以将移相角作为变换器模型输入与校正系统输出对接,并根据上文所求出迭代模型,与控制器的迭代方程联立,可以得到方程组为

式中,k_p为控制器的比例系数;V_ref为参考输出电压。

可以将所得方程组提取出系数矩阵,即系统的雅可比矩阵,然后对该矩阵的特征值进行求解,最终来判定系统的稳定性。其雅可比矩阵和特征方程表示如下

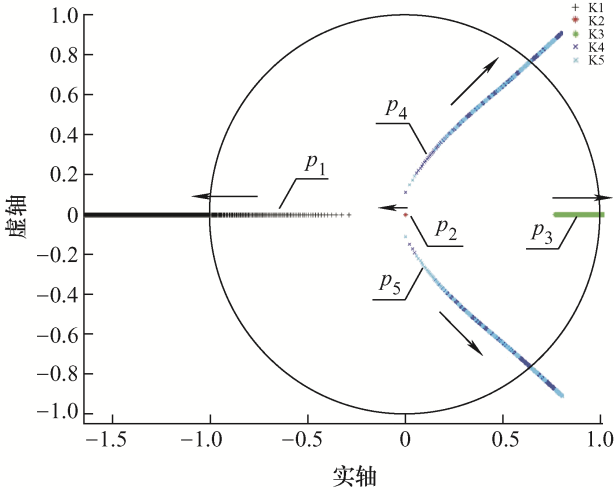
本文提出的PSFB-CDSR变换器的设计参数如表1所示。由此在限制系统其他参数不变的情况下,且固定R_e=200 mΩ,R_l=0.6 Ω,V_ref=12 V参数不变,调整校正系统的参数k_p,观察其对系统稳定性的影响,系统特征根轨迹随着k_p增大而变化的情况如 图8所示。由于系统的雅可比矩阵为5阶矩阵,因此得到5个特征根：p₁、p₂、p₃、p₄和p₅。其中p₁、p₂和p₃为单根,p₄和p₅为共轭复根,p₁、p₃和共轭根都对k_p参数变化表现明显,并且这些根都随着k_p的增大由单位圆内部逐渐向着穿出圆外的方向运动,而靠近零点的特征根p₂则几乎保持不变。在k_p>0.414时,特征根p₃穿出单位圆外。定义使得│p│=1的k_p为临界参数,用k_p,ed表示。当k_p>0.414时,系统不能以周期1稳定运行,当k_p<0.414时,系统能够稳定运行。

通常比例参数k_p设置较小,系统的稳定裕度较宽,但是同时也带来动态响应速度较慢的问题。为此要使系统能够及时地跟踪参考值,需要在保证系统稳定的前提下尽可能增大k_p。除此之外,硬件参数以及电路的工作条件一般认为在硬件设计完成和电路测试完成后基本保持不变,但是变换器的输出电压和输出负载通常会随着不同的工况而发生较大的变化,所以必须要分析这两项条件变化对于系统稳定性产生的影响,直接用于指导变换器的设计。

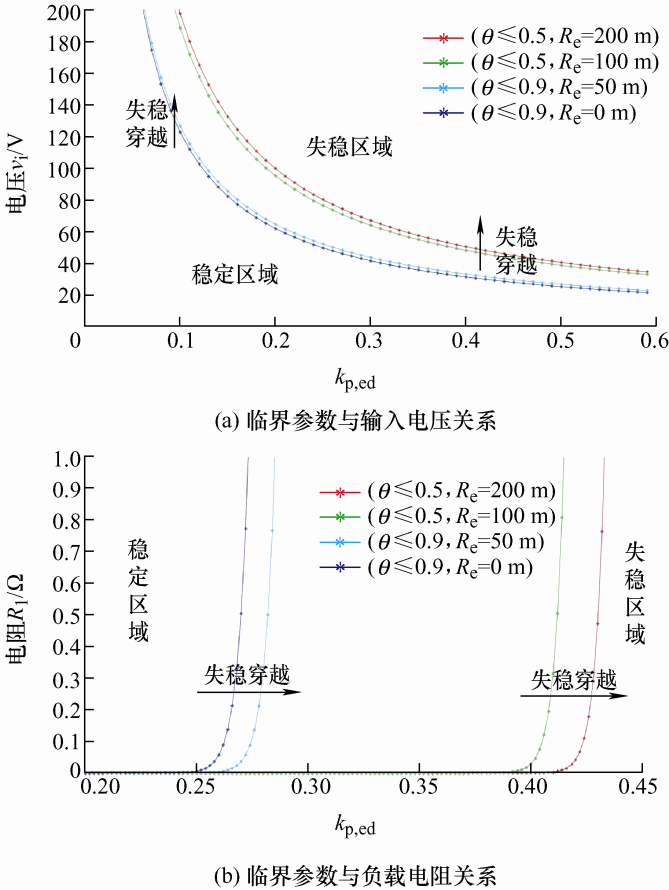
改变不同的输入电压或输出负载参数,固定其他参数,可以得出变换器运行的临界曲线,如图9所示。图9a为临界参数随输入电压变化的关系曲线,固定R_l=0.6 Ω,边界曲线右上方为失稳区域,左下方为稳定区域,图9中对比了无寄生电阻,寄生电阻分别为50 mΩ、100 mΩ和200 mΩ四种情况下的结果,可以看出临界k_p,ed总体随输入电压的增大而减少,虽然从局部看来线路中存在的寄生电阻越大,得到的稳定区域面积就越大,但事实上在线阻为100 mΩ,移相角大于0.6时,就已有特征根整体穿出单外圆外,系统已无法稳定工作,所以将移相角限制在了0.5以内。图9b为临界参数随负载电阻变化的关系曲线,固定v_i=48 V,边界曲线左上方为稳定区域,右下方为失稳区域,同样对比了四种寄生电阻的情况,当闭环系统在某一个确定的(k_p,R_l)的组合下稳定工作时,若负载电阻减小,则有可能自下向上越过稳定边界,使得变换器失去稳定;若负载电阻增大,即对应(k_p,R_l)点自上而下移动,则系统始终保持稳定^[8]。

因此PSFB-CDSR变换器在闭环控制器设计的时候,需要考虑到最恶劣的工况,即根据可能出现的最大输入电压进行设计。对于负载电阻较小时,变换器输出的功率较大,存在可能使系统穿越稳定边界,所以需要根据最大负载进行设计。

为了验证本文所提模型的有效性,在Saber中搭建功率以及逻辑驱动电路,在Matlab中搭建控制器系统进行联合仿真。电路参数与表1所设计参数相同,固定负载电阻R_l=0.6 Ω,寄生电阻R_e= 200 mΩ,V_ref=12 V,k_p=0.2,改变输入电压v_i分别为48 V、72 V、96 V、20 V、144 V。根据之前模型计算结果,各种输入电压的临界参数k_p如表2所示。

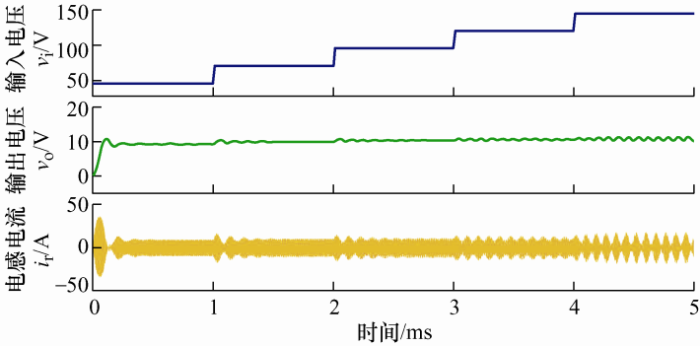
由图10可知,输入电压从48 V开始,每隔1 ms进行一次跃变,增加24 V,在当输入电压增加到96 V之后,输出电压与变压器原边电流,即谐振电感电流,已经明显出现振荡现象。因为控制器只有比例环节,未设置积分环节,所以系统会出现一定的静差,图10中表现为2 V左右,但不影响系统的稳定性分析^[8]。

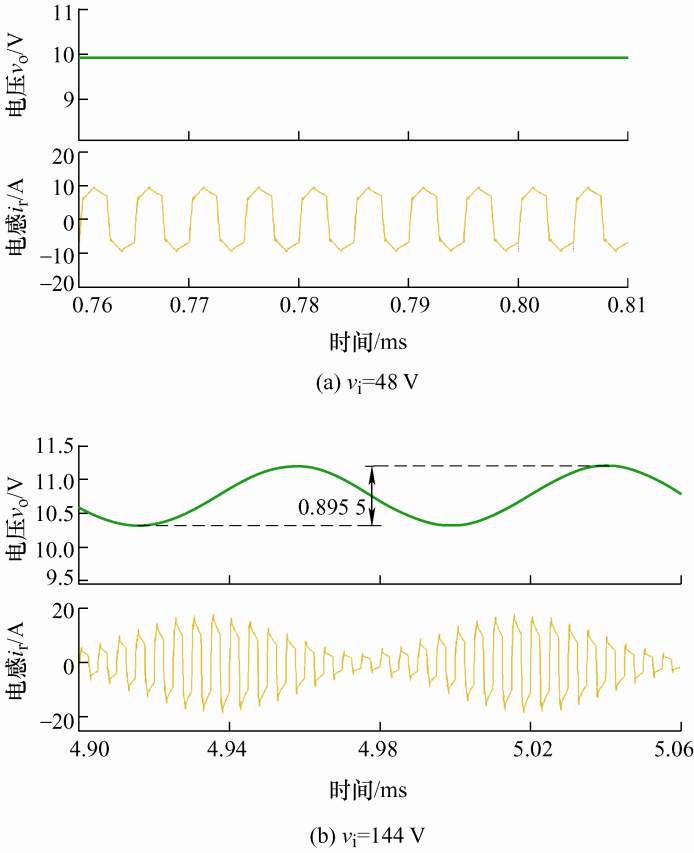
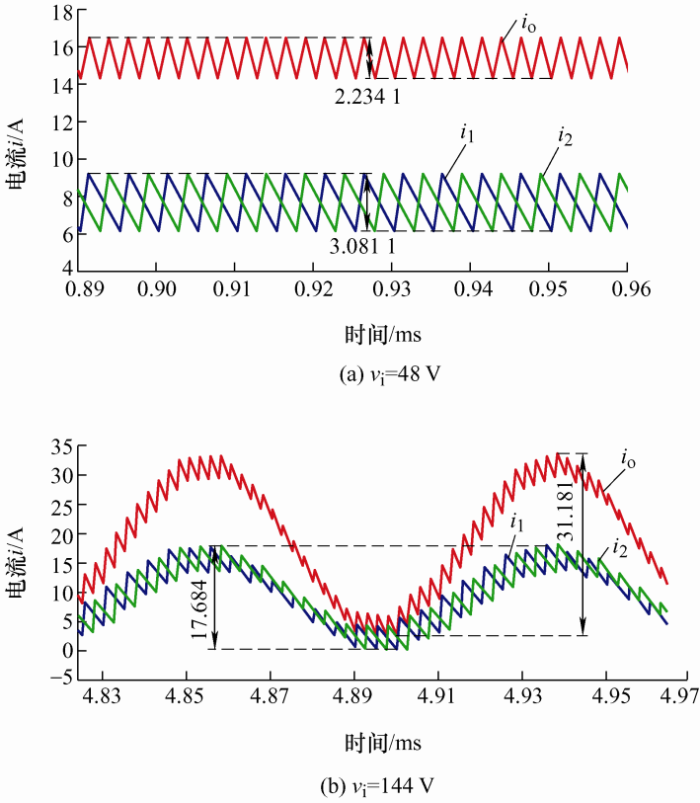
其他参数不变,图11对比了输入电压为分别48 V和144 V两种条件下的输出电压和谐振电感的电流波形,图12对比了两种条件下的滤波电感电流与输出电流。在输入48 V条件下输出电压稳定,纹波较小,且谐振电感电流波形与上一周期一致,两滤波电感电流i₁和i₂将电流均分,叠加在一起纹波对消,使输出电流i_o纹波减小;而在输入144 V条件下,输出电压出现明显振荡,纹波电压已达到0.9 V,谐振电感电流已无法与上一周期达到一致,且滤波电感电流也出现低频量扰动,最终使电流纹波急剧增大,系统已经失稳。

通过上述分析,对于闭环工作的PSFB-CDSR变换器,如果出现输入电压增大,则可能使系统失稳,与上文分析一致。相反地,增大控制器中k_p参数也会使得整个系统失去稳定。

本文从PSFB-CDSR变换器的工作原理出发,对其复杂模态进行简化,建立能够精准刻画变换器储能器件状态转移特性的等效模型,具有直观性和准确性;并在此基础上对原边移相全桥电流环流中存在的寄生电阻进行分析,精准地刻画该寄生电阻对于功率特性以及稳态特性的影响;然后考察等效电路模型在离散域中状态方程的特征根变化情况,得到在不同输入输出条件下对稳定裕度的影响。最后,通过仿真结果表明了该等效电路的精确性以及结论分析的正确性。