电气工程学报, 2021, 16(2): 108-114 doi: 10.11985/2021.02.014

电机与电器

电极旋转情况下真空电弧阳极熔蚀过程的数值仿真与分析*

马涛,1, 侯磊,1, 许杨勇,2, 祁天星,1, 杨天阔,1, 齐庆峰,3, 刘学识,4, 娄博威,4

1.河北省电力有限公司雄安新区供电公司 雄安新区 071000

2.浙江省电力有限公司检修分公司 杭州 310000

3.许继集团有限公司 许昌 461000

4.沈阳工业大学电气工程学院 沈阳 110870

Numerical Simulation and Analysis of the Anodic Etching Process of Vacuum Arc under the Condition of Electrode Rotation

MA Tao,1, HOU Lei,1, XU Yangyong,2, QI Tianxing,1, YANG Tiankuo,1, QI Qingfeng,3, LIU Xueshi,4, LOU Bowei,4

1. Xiong’an New Area Power Supply Company of Hebei Electric Power Co., Ltd., Xiong’an New Area 071000

2. Maintenance Branch of Zhejiang Electric Power Co., Ltd., Hangzhou 310000

3. Xuji Group Co., Ltd., Xuchang 461000

4. School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870

收稿日期: 2020-10-10   修回日期: 2021-04-12  

基金资助: * 国网河北省电力有限公司科技资助项目.  kj2019-013-Ⅱ

Received: 2020-10-10   Revised: 2021-04-12  

作者简介 About authors

马涛,男,1979年生,工程师。主要研究方向为电气工程及其自动化。E-mail： xa_mat@he.sgcc.com.cn

侯磊,男,1986年生,男,硕士。主要研究方向为能源互联网、综合能源和智能用电。E-mail： 705608320@qq.com

许杨勇,男,1980年生,硕士,高级工程师。主要从事超(特)高压输电线路检修运维工作。E-mail： 823802645@qq.com

祁天星,男,1993年生,硕士。主要研究方向电力系统及其自动化。E-mail： 920519860@qq.com

杨天阔,男,1991年生,硕士研究生,工程师。主要研究方向为电气工程及其自动化。E-mail： xa_yangtk@he.sgcc.com.cn

齐庆峰,男,1977年生。主要研究方向为新能源及节能技术。E-mail： qqfboy@126.com

刘学识,男,1997年生,硕士。主要研究方向为电器智能化。E-mail： 383675768@qq.com

娄博威,男,1997年生,硕士。主要研究方向为电器电弧理论。E-mail： 806608947@qq.com

摘要

对真空灭弧室中阳极触头的三维几何模型进行建模与分析,为了讨论电极旋转对真空电弧及阳极热过程的影响,建立了数学模型来模拟阳极表面熔化、蒸发时的相变过程,采用多孔介质描述方法以便于对固-液混合区域进行处理。由热过程的数值模拟可知,旋转电极表面温度、熔池面积以及熔池深度与热过程的时间呈正相关;电极转速越快,则阳极表面最高温度以及阳极表面熔池面积越小,阳极表面温度分布更加均匀,以此仿真模型为评估断路器的开断容量提供理论依据。

关键词： 真空电弧 ; 阳极烧蚀 ; 表面温度 ; 仿真研究

Abstract

A three-dimensional geometric model of anode contact of vacuum circuit breaker is established and analyzed in this paper. To analyze the influence of electrode rotation on vacuum arc and anode thermal process, a physical model of phase transformation process is established for the melting and evaporation of anode surface. The solid-liquid mixing area is treated by the description method of porous media, and the numerical simulation of anode thermal process is carried out, concluding that with the increase of time, the anode surface temperature is increasing, molten pool is developing, molten pool depth is deepening, in addition, with the increase of electrode speed, the highest temperature on the surface of the contact and the size of the molten pool are reducing, and the temperature distribution is more uniform. This simulation model can be an academic foundation to research the breaking capacity of circuit breaker.

Keywords： Vacuum arc ; anodic ablation ; surface temperature ; simulation research

PDF (1618KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

马涛, 侯磊, 许杨勇, 祁天星, 杨天阔, 齐庆峰, 刘学识, 娄博威. 电极旋转情况下真空电弧阳极熔蚀过程的数值仿真与分析*. 电气工程学报[J], 2021, 16(2): 108-114 doi:10.11985/2021.02.014

MA Tao, HOU Lei, XU Yangyong, QI Tianxing, YANG Tiankuo, QI Qingfeng, LIU Xueshi, LOU Bowei. Numerical Simulation and Analysis of the Anodic Etching Process of Vacuum Arc under the Condition of Electrode Rotation. Journal of Electrical Engineering[J], 2021, 16(2): 108-114 doi:10.11985/2021.02.014

1 引言

真空电弧本质是真空介质中的金属蒸气电弧,其产生机理也不同于其他气体介质电弧[1]。真空电弧的广泛应用体现在许多方面,如：真空灭弧室、真空镀膜以及相控真空开关等其他真空环境。对真空电弧的数学物理模型进行描述,并以此模型进行数值仿真是非常重要的分析与研究方法,此方法也逐渐受到越来越多专家与学者的青睐,并且不断被完善与改进。

在真空电弧燃烧时,等离子体中的电子和离子将自身的能流作用在阳极表面,导致阳极表面温度不断上升。当其温度上升到足够高时会产生熔池现象;当其温度上升至触头材料沸点时,阳极表面会喷射金属蒸气;在高温、高场强的作用下,带电粒子因碰撞电离而产生新的等离子体,使电极间隙绝缘能力减弱;若此时恢复电压较高,则会发生重击穿并导致开断失败[2,3,4,5,6]。

MILLER[2]曾对大量真空电弧试验结果进行对比与归纳,最终总结出四种阳极模式：扩散态电弧模式、点状斑点模式、阳极斑点模式以及集聚弧模式。小电流时电弧为扩散态,阴极斑点发射的电子、金属离子和中性粒子几乎充满极间,阳极并不活跃,是等离子体的接收器;电流等级上升时阳极开始活跃,逐渐产生阳极斑点并向极间发射金属蒸气,促进等离子体形成、加剧触头烧蚀程度;当电流等级升高到阳极斑点模式时,阳极表面将喷射更多金属蒸气,并出现明显的烧蚀。在此阳极斑点模式下,若真空断路器体积较小,还会发展为集聚型电弧模式[7,8,9,10,11,12]。

真空断路器的开断容量会受到阳极热过程的 影响。阳极斑点是判断断路器开断的重要依据。文献[13,14,15,16]以质量、动量、能量三大守恒方程为基础建立了电弧稳态模型,仿真分析出阳极能流密度与阳极表面温度的分布情况,并且讨论了瞬态阳极热过程的数学物理模型,对阳极极板的外部能流密度、内部热传导、电子能量平衡关系以及重离子平衡关系进行了求解。文献[17]用一维建模分析了电极的相变过程。文献[18]讨论了不同能流密度情况下,阳极热过程对电弧的影响。文献[19]在文献[13,14,15,16]的基础上分析了阳极鞘层电势在不同燃弧参数影响下的变化规律。文献[20]通过ANSYS软件对断路器分断时的阳极热过程进行了瞬态模拟。文献[21]仿真了磁场作用时阳极的偏烧情况,总结了磁场对阳极烧蚀现象的影响规律。

真空断路器的电极旋转开断方式可以使等离子体跟随着电极做旋转运动。通过此旋转运动,电弧能量将作用于电极表面的不同位置,阳极热过程会产生与常规开断方式不同的影响规律[22]。本文以COMSOL Multiphysics软件建立了瞬态真空电弧三维阳极模型,对高电流等级时阳极热过程进行仿真,并讨论真空电弧弧后阳极相变过程,对触头表面的温度分布和熔池的变化规律进行了分析与总结。

2 仿真模型

2.1 物理模型

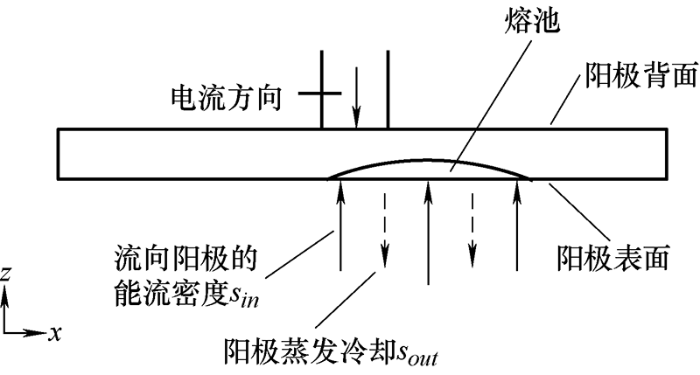
真空开关阳极热过程的物理模型如图1所示。此物理模型主要包括触头片、导电杯以及导电杆。在真空电弧几毫秒的快速开断过程中,可以忽略导电杯以及导电杆的热能影响,因此只针对触头片进行建模分析。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   阳极热过程物理模型


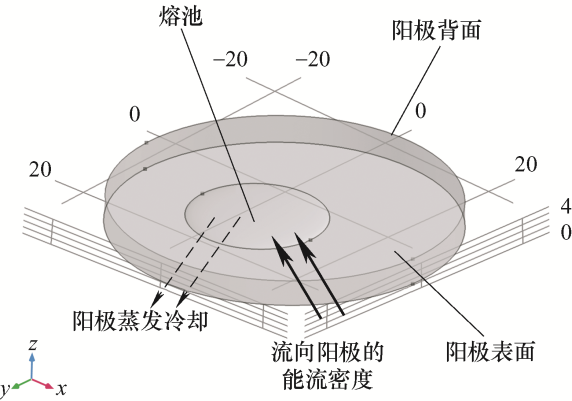
建立阳极热过程的瞬态模型可以分析阳极熔池现象。瞬态模型仿真时间为工频电流的一个半波时间,即10 ms。对于仿真中电极材料以及电极相关参数的设置如下：电极材料为纯铜,其半径为25 mm、厚度为4 mm。物理模型如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   阳极触头几何模型(mm)


为便于分析,对模型提出以下假设：① 阳极熔化时向外飞溅的液滴以及蒸发喷射的金属蒸气忽略不计,即在阳极热过程阶段遵循质量守恒定律;② 阳极喷射的金属蒸气对电弧等离子体的影响忽略不计;③ 阳极相变时的形变忽略不计;④ 忽略阳极与周围的热交换与热辐射,只考虑阳极触头在喷射金属蒸气过程中损失的热量;⑤ 相变时的融化潜热不可忽略,应该考虑其影响。

2.2 数学模型

若真空断路器开断电流较大,阳极表面就会产生高温的阳极斑点。由于高温的作用,固态金属会转变为液态金属,并且形成阳极熔池。在熔池的过程中,阳极可分为三个区域：固态区、固液混合区以及液态区。流入阳极的能量越大,阳极表面温度则越高,熔池区域越大,固液分界面也发生移动。

质量守恒、动量守恒以及能量守恒是材料相变过程中遵循的流体力学方程,可以据此推导相变时的控制方程。

2.2.1 质量守恒方程

由于不计阳极熔化和金属蒸气的质量损失,故有如下质量守恒方程

$\frac{\partial \rho }{\partial t}+\nabla \centerdot (\rho U)=0$

式中,ρ为铜金属的密度;U为运动速度矢量。

2.2.2 动量守恒方程

由于忽略重力、电磁力等外力影响,故动量守恒方式如下

$\frac{\partial \left( \rho U \right)}{\partial t}+\nabla \centerdot (\rho UU)=-\nabla p-\frac{2}{3}\nabla \centerdot (\mu \nabla \centerdot U)$

式中,p为压力项;μ为黏性系数。

2.2.3 能量守恒方程

真空电弧燃烧时,阳极与周围的能量交换主要包括：电子、离子输入的能流,电极的热量传导,电极表面的热辐射以及电极喷射金属蒸气时的能量损失。单位体积阳极触头能量守恒方程如下

$\frac{\partial \left( \rho H \right)}{\partial t}+\nabla \centerdot (\rho H)=\nabla \centerdot (k\nabla T)+S$

式中,H为阳极的热焓;k为阳极材料热导率;T为温度;S为热源项。

电极材料的热焓H包括两个部分

$H=h+\beta L$

式中,h为显焓;β为液相比例;L为材料的潜热。

由于阳极固液混合区的存在,因此假设此区域为多孔介质。从多孔介质的流动角度来反映固相和液相的转化,β是熔化时的流体分数,反映流体中固液组分的比例,表达式如下

$\left\{ \begin{align} & \beta =0\ \ \ \ \ \ \ \ \ \ \ \ T<{{T}_{s}} \\ & \beta =\frac{T-{{T}_{s}}}{{{T}_{l}}-{{T}_{s}}}\ \ \ \ {{T}_{s}}<T<{{T}_{l}} \\ & \beta =1\ \ \ \ \ \ \ \ \ \ \ \ {{T}_{l}}<T \\ \end{align} \right.$

式中,Ts为电极固相温度;Tl为电极液相温度。电极的熔点是纯金属发生等温相变的临界点,即Ts=Tl。此时,式(5)将无意义。在此温度附近构造温度区域[T-Tε,T+Tε],以保证计算时的收敛性。

熔池的出现是阳极熔化后的重要现象。在电极热过程中,液相和固相之间存在能量交换。此过程能量守恒方程如下

$\rho {{C}_{p}}\frac{\partial T}{\partial t}+\nabla \centerdot (k\nabla T)=0$

仿真中极板材料为铜,根据数据[11,12],有关参数如表1所示。

表1   铜材料物理参数

物理参数数值
固相温度(熔点)Ts/K1 356
液相温度Tl/K1 489
固液相变潜热L/(J/kg)3.3×104
固相比热容Cps /[J/(kg·K)]380
液相比热容Cpl /[J/(kg·K)]494
固相热导率λs /[W/(m·K)]372
液相热导率λl /[W/(m·K)]174
固相密度ρs /(kg/m3)8 960
液相密度ρl /(kg/m3)8 000

新窗口打开| 下载CSV


3 边界条件

3.1 阳极表面边界条件

阳极表面与周围的热交换主要为两个部分：一是电弧中电子、离子能流的输入,其值从电弧中心到阳极边缘逐渐递减;另一部分是电极喷射金属蒸气时的能量损失。通过对这两部分能量的分析可知,输入的能流密度表达式如下

${{S}_{in}}={{S}_{e}}+{{S}_{i}}$
${{S}_{e}}={{n}_{e}}{{v}_{z}}\left( 2k{{T}_{e}}+{{\phi }_{w}} \right)$
${{S}_{i}}={{n}_{i}}{{u}_{z}}\left( \frac{1}{2}{{m}_{i}}u_{z}^{2}-e{{Z}_{i}}{{\phi }_{sh}}+\sum{{{f}_{Z}}{{\phi }_{Z}}-{{Z}_{i}}}{{\phi }_{w}}+{{\phi }_{v}} \right)$

式中,Sin为输入阳极表面的能流密度之和;Se为电子能流密度;Si为离子能流密度;ne为电子数密度;vz为电子沿z轴方向的速度分量;k为玻尔兹曼常数;Te为电子温度;ϕw为电子功函数,为4.29 eV;ni为离子数密度;uz为离子沿z轴方向的速度分量;mi为离子质量;e为电子电荷;Zi为离子平均电荷数,为1.85;ϕsh为阳极鞘层电势;fZ为Z价离子占总数的百分比;ϕZ为Z价电子的电离能;ϕv为蒸发能,为3.12 eV。由于无法确定能流密度的具体表达式,在此用阶跃函数作为其近似表达,并在跳跃点进行平滑处理以保证仿真收敛。

阳极斑点出现时,阳极喷射的金属蒸气流量表达式如下

$\frac{1}{4}nv=\frac{1}{4}\frac{p}{kT}\sqrt{\frac{8kT}{\text{ }\!\!\pi\!\!\text{ }m}}=\frac{p}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }kmT}}$

喷射金属蒸气损失的能量表达式为[13]

${{S}_{out}}\text{=}q\frac{p}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }kmT}}$

式中,Sout为喷射等离子体时,阳极表面损失的能量;T为阳极表面温度;q为蒸发时单个原子所带走的热量,q=5.1×10-19 J;p为饱和蒸气压。

因此阳极表面流入的总能量为

$Q={{S}_{in}}-{{S}_{out}}$

3.2 阳极背面边界条件

与极板厚度相比,熔池深度往往都很浅,因此可以忽略熔池深度。阳极背面在较短的时间内温度变化不明显,因此按照绝热处理

$n\centerdot (\lambda \nabla T)=0$

3.3 阳极背面边界条件

最大能流密度通常在电弧中心区域,所以短时间内阳极边界不会产生较大的能量,因此阳极边缘也按照绝热处理

$n\centerdot (\lambda \nabla T)=0$

设阳极表面温度初始值为室温,即273.15 K。

4 仿真结果与分析

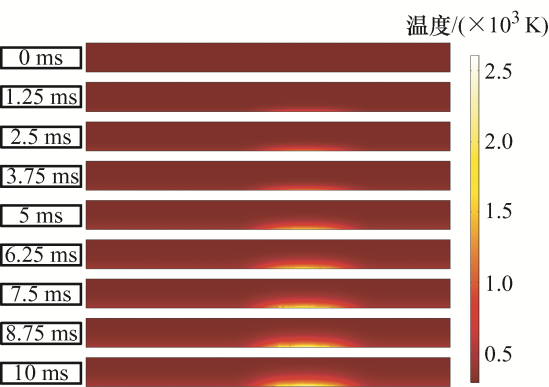
阳极表面能流密度峰值为1.19×108 W/m2,阳极触头温度及熔池的数值模拟结果如图3和图4所示。结合图3与图4可知,在0~5 ms时,虽然阳极表面温度在逐渐升高,但是阳极表面温度还未达到触头材料熔点;当仿真时间进行到5 ms时,部分阳极触头区域已经到达材料熔点并出现相变现象,可见明显的固-液分界面。在10 ms时,出现阳极表面温度最大值2 560 K,此时触头背面温升仅为350 K左右,能流密度几乎未传递到阳极背面,熔池深度为0.55 mm左右,阳极触头并未因熔池出现较大形变。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   阳极触头温度变化


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   阳极触头熔池发展


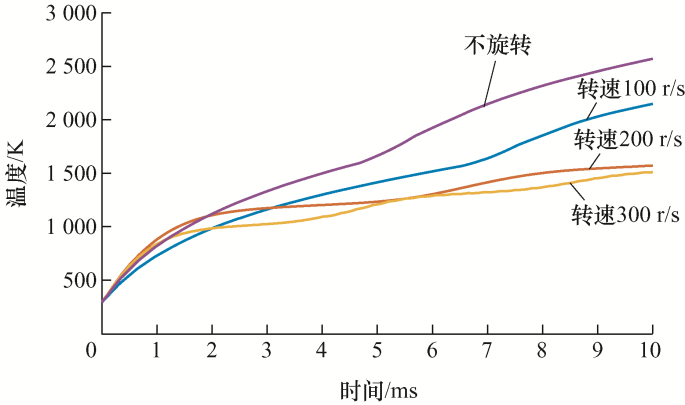
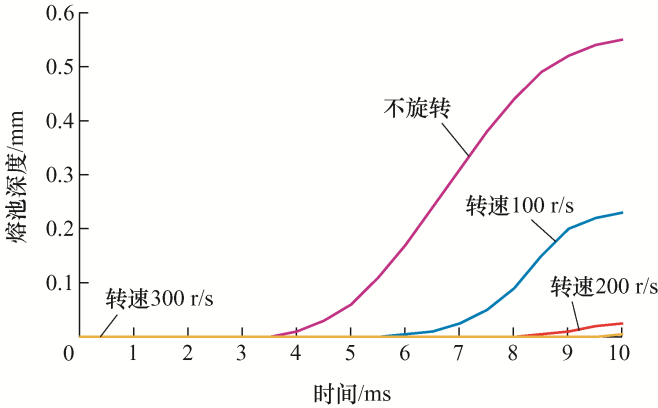
通过对电极在不同转速时的仿真,得到触头旋转对阳极表面温度及熔池的影响规律如图5和图6所示。结合图5与图6可知,阳极表面温度的上升速度随着电极转速的增加而逐渐降低,触头温度升高到材料熔点所需要的时间也越来越长;电极无旋转时,阳极表面在5 ms时开始出现熔池现象,最后温度上升至约2 560 K,熔池深度在约9 ms时趋于稳定,熔池深度约为0.55 mm;当电极转速为100 r/s时,在约7 ms时才出现熔池,在10 ms时,阳极表面温度达到了2 200 K,熔池深度为0.23 mm;当电极转速增大为200 r/s时,阳极表面温度下降至触头材料的熔点1 600 K附近,出现熔池的时间延后至9 ms左右;当电极转速继续增加时,阳极表面温度将不能达到触头材料的熔点,触头表面温度也不再发生明显变化,熔池也不再产生。由于相变的吸热现象,熔化部分的温度上升缓慢。当触头表面温度超过触头材料熔点时,蒸发的金属蒸气又散失了部分热量,因此减缓了升温的趋势,温度的最大值也由于蒸发过程的限制而有所降低。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   阳极表面温度变化


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   阳极熔池深度的变化


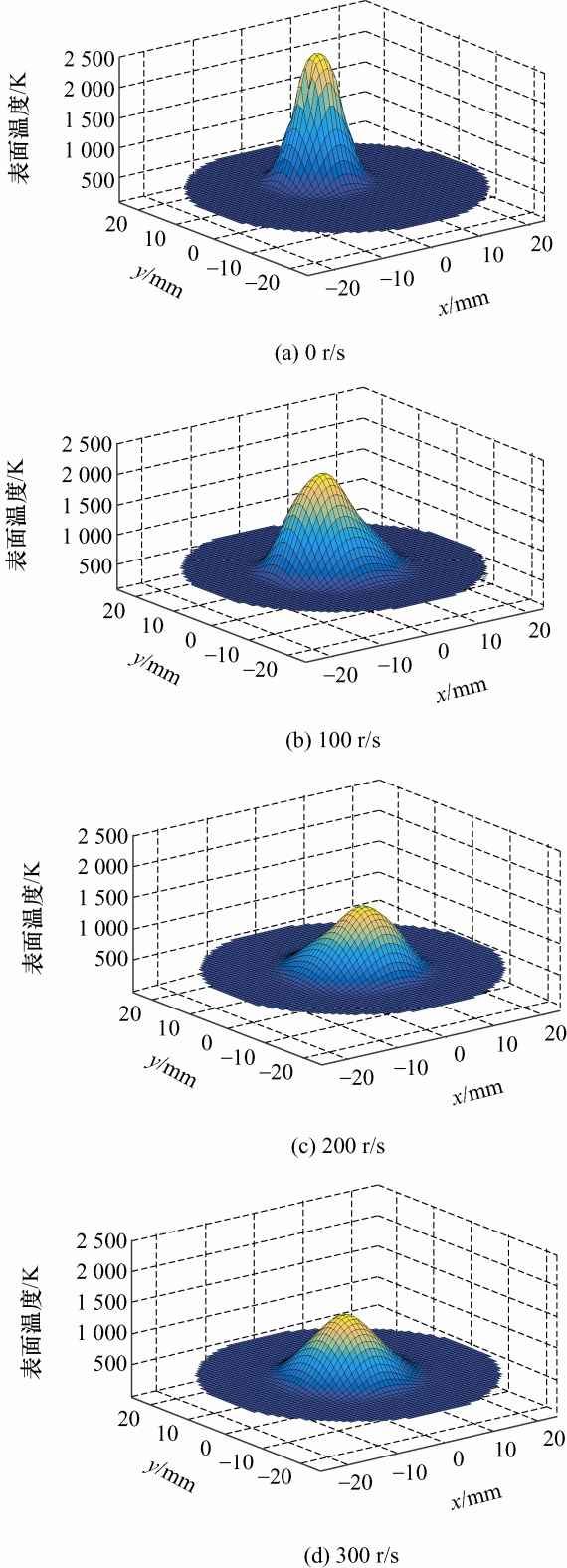
电极转速对阳极表面温度分布的影响情况如 图7所示。从图7可知,电极转速的增加使得阳极表面最高温度逐渐下降,其温度分布也更加均匀。电极的旋转作用使得阳极能流密度分散在更大的区域,避免了局部区域温度过高的影响,阳极表面受热也更加均匀;由于旋转电弧更利于蒸发和辐射,并散失更多的能量,因此也有助于阻断阳极斑点的形成。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   电极旋转速度对阳极表面温度的影响


5 结论

本文对阳极触头旋转时的热过程进行分析,建立三维模型对阳极热过程进行计算,对阳极的相变以及发射金属蒸气的过程进行考虑,采用多孔介质法处理固-液混合区。通过对阳极表面相变过程的数学物理模型进行分析,以及对数值模拟结果进行对比后,得到如下结论。

(1) 阳极表面温度在能流密度输入的过程中逐渐升高。当温度升高到触头材料熔点时会产生相变与熔池现象;阳极熔池会随着时间的进行而不断地发展,最终熔池深度达到0.55 mm左右。该熔池深度较小,与阳极触头的厚度相比可以忽略。此外,阳极表面温度变化明显,触头背面以及侧边未产生明显的温度变化。

(2) 在电极转速增加时,阳极表面温度的上升速度逐渐变慢,阳极表面温度最大值逐渐降低,延缓了熔池出现的时间,熔池深度也更小;由于电极的旋转作用,从而导致阳极温度分布更加均匀,这有利于阳极通过蒸发和对外辐射散失更多的热量,并能阻断阳极斑点的形成。

参考文献

BOXMAN R L, SANDERS D M, MARTIN P J, et al.

Handbook of vacuum arc science and technology fundamentals and applications

[M]. New Jersey:Noyes Publications, 1996.

[本文引用: 1]

MILLER H C.

Discharge modes at the anode of a vacuum arc

[J]. IEEE Transactions on Plasma Science, 1983, 11(3):122-127.

DOI:10.1109/TPS.1983.4316238      URL     [本文引用: 2]

MATSUI Y, SANO A, KOMATSU H, et al.

Vacuum arc phenomena under various axial magnetic field and anode melting

[C]// 24th International Symposium on Discharge and Electrical Insulation in Vacuum. Braunschweig,Germany:IEEE, 2010:324-327.

[本文引用: 1]

BEILIS I I, BOXMAN R L, GOLDSMITH S.

A hot refractory anode vacuum arc:Nonstationary plasma model

[J]. IEEE Transactions on Plasma Science, 2001, 29(5):690-694.

DOI:10.1109/27.964455      URL     [本文引用: 1]

BEILIS I I, BOXMAN R L, GOLDSMITH S.

Interelectrode plasma evolution in a hot refractory anode vacuum arc:Theory and comparison with experiment

[J]. Physics of Plasmas, 2002, 9(7):3159-3170.

DOI:10.1063/1.1483844      URL     [本文引用: 1]

NIWA Y, SATO J, YOKOKURA K.

The effect of contact material on temperature and melting of anode surface in the vacuum interrupter

[C]// International Symposium on Discharges and Electrical Insulation in Vacuum. Xi’an,China:IEEE, 2000:524-527.

[本文引用: 1]

SCHADE E, SHMELEV D, KLEBERG I.

Numerical modeling of the heat flux to the anode of high-current vacuum arcs

[C]// 21st International Conference on Electrical Contacts(ICEC2002). Zurich,Switzerland:IEEE, 2002:518-525.

[本文引用: 1]

SHASHURIN A, BEILIS I I, BOXMAN R L.

Heat flux to an asymmetric anode in a hot refractory anode vacuum arc

[J]. Plasma Sources Science and Technology, 2010, 19(015002):1-8.

[本文引用: 1]

SHI Z, JIA S, DONG H, et al.

Simulation of the thermal process of anode in drawn vacuum arc

[J]. IEEE Transactions on Plasma Science, 2007, 35(4):920-924.

DOI:10.1109/TPS.2007.896911      URL     [本文引用: 1]

黄小龙, 王立军, 贾申利, 等.

纵向磁场和外部横向磁场共同作用下真空电弧偏移与阳极偏烧现象的仿真研究

[J]. 中国电机工程学报, 2014, 34(6):941-946.

[本文引用: 1]

HUANG Xiaolong, WANG Lijun, JIA Shenli, et al.

Simulation research of deflection phenomenon of vacuum arc and anode erosion under the combined action of axial magnetic field and external transverse magnetic field

[J]. Proceedings of the CSEE, 2014, 34(6):941-946.

[本文引用: 1]

王立军, 贾申利, 史宗谦, 等.

真空电弧磁流体动力学模型与仿真研究

[J]. 中国电机工程学报, 2005, 25(4):113-118.

[本文引用: 2]

WANG Lijun, JIA Shenli, SHI Zongqian, et al.

MHD model and simulation research of vacuum arc

[J]. Proceedings of the CSEE, 2005, 25(4):113-118.

[本文引用: 2]

BRANDES E A, BROOK G B.

Smithells metals reference book

[M]. Burlington:Elsevier Butterworth Heinemann, 1998.

[本文引用: 2]

WANG Y, DAMSTRA G C.

Noise arc voltage and dynamic constriction of high-current vacuum arcs

[J]. Journal of Physics D:Applied Physics, 1991, 24(12):2179-2189.

DOI:10.1088/0022-3727/24/12/008      URL     [本文引用: 3]

ECKER G.

Anode spot instability I:The homogeneous short gap instability

[J]. IEEE Transactions on Plasma Science, 1974, 2(3):130-146.

DOI:10.1109/TPS.1974.4316826      URL     [本文引用: 2]

李国明.

大电流真空电弧阳极熔蚀过程的数值仿真与分析

[J]. 电气工程学报, 2019, 14(1):41-45.

[本文引用: 2]

LI Guoming.

Numerical simulation and analysis of anode erosion process under high-current vacuum arcs

[J]. Journal of Electrical Engineering, 2019, 14(1):41-45.

[本文引用: 2]

胡秋生, 贺家敏, 张鑫, 等.

真空断路器触头电磨损在线检测系统研究

[J]. 电气工程学报, 2018, 13(1):43-48.

[本文引用: 2]

HU Qiusheng, HE Jiamin, ZHANG Xin, et al.

The on-line monitoring application study of vacuum circuit breakers contact system

[J]. Journal of Electrical Engineering, 2018, 13(1):43-48.

[本文引用: 2]

WANG Zhenxing, TIAN Yunbo, MA Hui, et al.

Decay modes of anode surface temperature after current zero in vacuum arcs-part II:Theoretical study of dielectric recovery strength

[J]. IEEE Transactions on Plasma Science, 2015, 43(10):3734-3743.

DOI:10.1109/TPS.2015.2467158      URL     [本文引用: 1]

WANG Lijun, JIA Shenli, LIU Yu, et al.

Modeling and simulation of anode melting pool flow under the action of high-current vacuum arc

[J]. Journal of Applied Physics, 2010, 107(11):113-306.

[本文引用: 1]

YAO X, WANG J, GENG Y, et al.

An influence of an ambient magnetic field induced by a nearby parallel conductor on high-current vacuum arcs

[C]// Proceedings of the 25th International Symposium on Discharges and Electrical Insulation in Vacuum. Tomsk, Russia: Institute of High-current Electronics Siberian Branch Russian Academy of Sciences, 2012:337-340.

[本文引用: 1]

HAUSER A, HARTMANN W, LAWALL A, et al.

Development of a FEM simulation of axial magnetic field vacuum arcs

[C]// Proceedings of the 23rd International Symposium on Discharges and Electrical Insulation in Vacuum. Bucharest, Rumania: University “POLITEHNICA” of Bucharest, 2008:398-401.

[本文引用: 1]

GENTSCH D, SHANG W K.

High-speed observations of arc modes and material erosion on RMF- and AMF-contact electrodes

[J]. IEEE Transactions on Plasma Science, 2005, 33(5):1605-1610.

DOI:10.1109/TPS.2005.856514      URL     [本文引用: 1]

李显哲.

电极旋转情况下真空电弧磁流体动力学模型的仿真研究

[D]. 沈阳:沈阳工业大学, 2020.

[本文引用: 1]

LI Xianzhe.

Simulation study on the MHD model of vacuum arc with rotating electrodes

[D]. Shenyang:Shenyang University of Technology, 2020.

[本文引用: 1]

/

〈 〉