1 引言
拓扑是复杂网络的基本属性,能最直观反映网络的结构,复杂网络理论以往的主要研究对象为单个网络,直到BULDYREV等[3]对两个网络耦合而成的系统展开研究并提出相互依存网络的概念,并结合级联故障的交互过程进行研究,为分析耦合网络在级联故障下的相互影响提供了新思路[4],复杂网络研究的焦点也逐渐开始由单个网络转向多层网络[5]。此后,许多学者从攻击模式、相依网络耦合强度、相互依存等角度对耦合网络性能进行了研究[6,7,8]。文献[9]基于渗流理论对相依网络遭受攻击时的鲁棒性展开研究,指出相依网络在面对考虑相依关系节点度的攻击时的鲁棒性较弱。文献[10]对由无标度网络耦合成的相依网络的鲁棒性展开研究,并发现保护高度数节点的策略在提高相依网络鲁棒性中效果不明显,但是在单独的无标度网络中鲁棒性明显提高。文献[11]基于复杂网络理论比较了电力信息相互依存网络与单层电网的鲁棒性。文献[12]基于负载容量模型建立相依网络级联失效模型,并提出三种攻击策略,发现基于高负荷、高度数节点的攻击策略相较于随机攻击策略对相依网络的破坏能力强。文献[13]研究了在不同的级联机制下,攻击策略对相依网络鲁棒性的影响,发现非对称级联机制对相依网络的破坏能力强于对称级联机制下的。文献[14]基于节点负载分配,构建了级联负载相依网络模型,并发现负载分布均匀时,低负载节点更有可能触发级联故障的传播。文献[15]基于实际的网络环境研究由电力网和通信网耦合而成的网络在级联故障下的鲁棒性,并对单个网络中的节点进行分析从而确定网络中的关键节点。
上述研究在分析网络的鲁棒性时主要针对整个耦合网络而言,而耦合网络的鲁棒性由于信息网的加入而大大降低[16]。因此,本文主要研究单侧信息网在电力信息耦合网络中的鲁棒性,特别是当电力侧网络的拓扑结构不同时,对信息网鲁棒性的影响,并提出能够提高网络鲁棒性的保护策略。
2 相关参数定义
2.1 复杂网络相关概念
本文所用到的相关参数定义如下。
(1) 度数k:网络中某个节点的度k定义为与该节点相连接的边数。
(2) 度分布P(k):网络中节点度的分布情况,用分布函数P(k)表示,即一个随机选中的节点恰好为k的概率。
(3) 介数Bi:网络中某个节点i的介数即为所有最短路径中经过该节点的路径的数目占最短路径总数的比例。
2.2 信息网鲁棒性评估指标
在复杂网络理论中,网络裂解后节点数最多的子团称为最大连通子团[17]。最大连通子团的大小反映了网络抵御级联失效能力的强弱。定义网络在发生级联失效后信息网连通能力R作为衡量信息网在遭受攻击时的鲁棒性指标
式中,N表示信息网在发生级联失效之前的节点总数,而N'表示信息网发生级联失效后最大连通子团的节点数。R越大,表明网络连通性能越强,鲁棒性越强,反之越弱,网络遭受破坏传播范围越广。
3 电力信息耦合网络模型
电力信息耦合网络是由电力网和信息网耦合而成的二元复合系统。运用复杂网络理论,可将电力网模型和信息网模型抽象为拓扑图,电力网和信息网分别用${{G}_{P}}=({{V}_{P}},{{E}_{P}})$和${{G}_{C}}=({{V}_{C}},{{E}_{C}})$表示,将变电站、发电厂等视为电力节点VPi,电力输电线路视为电力边EP;将调度中心、通信站点等视为信息节点VCj,通信线路视为信息边EC。现有的电力-信息物理耦合网络模型主要有[4]“一一对应”相依网络模型、部分相依网络模型、多重相依网络模型、“一对多”相依网络模型、“多对多”相依网络模型等,这里仅考虑“一一对应”相依网络模型[3],即电力节点与信息节点按照一一对应的方式进行耦合连接,两者网络的节点为相互依存关系。电力信息物理融合系统中,信息层与物理层间的相互作用可以概括为能量依靠关系与3C(控制、通信、计算)功能依靠关系。能量依靠关系意味着信息层节点运行所需的能量由与其建立能量依靠关系的物理层节点提供,3C功能依靠关系意味着物理层节点的监控及调度的数据通信处理由与其建立3C功能依靠关系的信息层节点实现[18]。因此,这里用耦合连接边EP-C即表示电力网与信息网的耦合关系,若电力层节点VPi为信息层节点VCj提供运行所需能量,则EP-C,ij=1;若信息层节点VCj对电力层节点VPi进行监控,则EP-C,ji=1。电力信息耦合网络通过电力节点与信息节点间的相互依存关系实现了电力网与信息网的耦合。电力网和信息网拓扑关系可以分别用邻接矩阵表示$A={{({{a}_{ij}})}_{N\times N}}$、$B={{({{b}_{ij}})}_{N\times N}}$,在电力网中如果节点i和节点j间有连接,则aij=1,反之aij=0,信息网同理。因此,电力信息耦合网络可以建模为由电力网、信息网及耦合连接边组成的集合$({{G}_{P}},{{G}_{C}},{{E}_{P-C}})$。
表1 耦合网络组成类型
| 耦合网络 | 电力网 | 信息网 | |
|---|---|---|---|
| 小世界-118耦合网络(WS-118) | WS小世界网络 | 118节点网络 | |
| 无标度-118耦合网络(BA-118) | BA无标度网络 | 118节点网络 | |
| 随机-118耦合网络(ER-118) | ER随机网络 | 118节点网络 | |
4 基于负载容量的级联失效交互模型
4.1 节点负载容量及其分配策略
本文引入负载和容量[23]作为网络的结构负载,在不考虑负载可调参数和容量容许参数变化的情况下,分析耦合网络间的级联失效交互传播机理。
(1) 负载与容量
定义ki为节点i的度大小;${{\Gamma }_{i}}$为与节点i相连接的节点集合;n为网络节点总数。网络的节点i在发生级联失效前的初始负载为
节点i的容量定义为
式中,T为大于1的网络的容许参数。由于本文不讨论T值对网络鲁棒性的影响,所以这里T设为一个常数。
(2) 负载重分配
网络中若某一节点失效,则其负载将被分配到其他节点上,分配后的节点负载若超过本身节点的容量,则该节点失效。
失效节点i上的负载将按照分配概率Qji重新分配到与之相连的邻域节点j上,Qji定义为
根据分配概率,领域节点j收到的额外负载 ΔLji为
当节点i失效之后,它的相邻节点j的负载将 变为
完成负载分配的节点后,若负载超过节点容量,则视为故障节点。
4.2 级联失效交互过程
电力信息耦合网络的级联失效由网络中的某 些节点意外故障或受到攻击失效引起。参考文献 [3,18],结合渗流理论,将渗流过程类比于网络中除去点或边的连锁故障发展过程,对信息层节点和电力层节点做如下规定。
(1) 在节点负载不超过本身节点容量的情况下,与控制中心存在连接关系且属于信息网最大工作连通团,与电力节点存在能量依靠关系的信息节点视为可用节点。
(2) 在节点负载不超过本身节点容量的情况下,属于电力网的最大工作连通团且与信息节点存在3C功能依靠关系的电力节点视为可用节点。
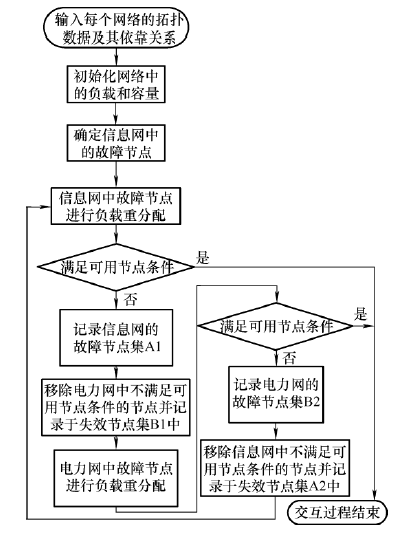
由于负载重分配和渗流过程两方面因素的影响失效节点的范围在信息网和电力网之间扩大,反复传递,产生级联故障,级联失效交互传播过程如图1所示。
图1
(1) 步骤一:设置信息网内的初始故障节点i,更新信息网拓扑结构。
(2) 步骤二:当信息网内的节点发生故障时,故障节点的负载将根据负载重分配方法(式(6))被分配到与之相连的节点上。如果重新分配后的节点负载超过节点本身的容量,则此类节点失效,同时搜索不满足可用节点规定条件的信息节点,记录在信息网的故障节点集A1内;如果信息网中节点符合可用信息节点规定条件,转到步骤六。
(3) 步骤三:由于步骤二中信息网内的部分节点失效,导致电力网中部分节点不满足可用节点规定条件而失效,将此类失效节点记录在失效节点集B1。
(4) 步骤四:步骤三中的失效节点将进行负载重新分配(式(6)),重新分配后超出容量的节点失效,同时搜索不满足可用节点规定条件的电力节点,记录在电力网的故障节点集B2内;若负载重分配后的节点符合可用节点规定条件,转到步骤六。
(5) 步骤五:根据步骤四的失效节点集B2,搜索信息网中不满足可用节点规定条件的节点,记录在失效节点集A2中,转到步骤二。
(6) 步骤六:耦合网络中无失效节点出现,电力信息耦合网络交互影响故障过程结束。
5 鲁棒性分析
下面首先分析耦合网络单侧电力网的节点度分布特性,再采用上述模型,以信息网鲁棒性为评估指标,对耦合网络信息网在随机节点攻击和高度数节点攻击下发生级联失效的鲁棒性进行仿真分析。
5.1 电力信息耦合网络电力侧网络的度分布特性分析
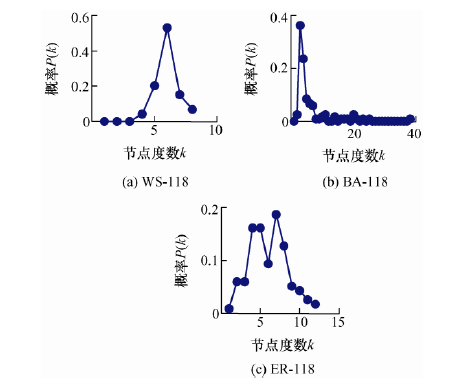
基于复杂网络理论对第3节的三种耦合网络单侧电力网的度分布特性进行分析,为研究网络的鲁棒性提供理论依据。图2分别为WS-118、BA-118和ER-118三种耦合网络电力侧的节点度数分布概率曲线,能反映节点连接在网络中的分布情况,横轴表示网络的节点度数k,纵轴表示度数为k的节点在网络中的概率。从图中可以看出WS-118的电
图2
力网和ER-118的电力网节点的最大度数和最小度数之间相差较小,表明两者网络整体结构分布较为均匀;而BA-118的电力网节点度数之间相差很大,节点最大度数高达38,节点最小度数为1,网络节点分布不均匀,节点度分布更广。
5.2 电力信息耦合网络信息侧鲁棒性分析
设定随机节点攻击和高度数节点攻击两种攻击模式对电力信息耦合网络故障交互过程进行模拟。其中随机节点攻击模式为随机选择信息网中10个节点作为初始攻击节点;高度数节点攻击模式为将信息网中的节点度数进行排序,依次将度数排名前10位的节点作为初始攻击节点后取平均值。每种攻击模式进行100次试验取平均值。
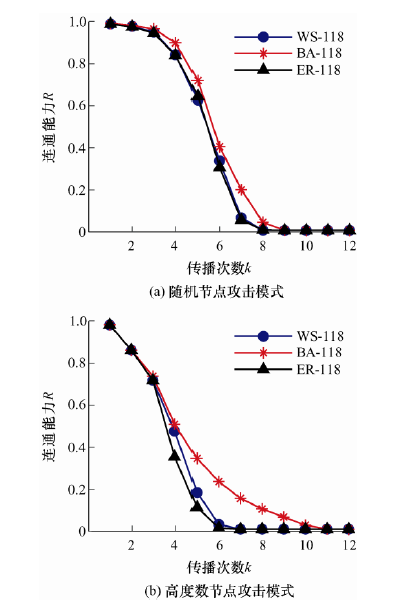
在对电力信息耦合网络信息侧进行鲁棒性分析时,分别用以上两种攻击模式攻击WS-118耦合网络、BA-118耦合网络、ER-118耦合网络,从信息网连通能力的角度对比以上三种耦合网络信息侧的鲁棒性。图3对比了WS-118耦合网络、BA-118耦合网络、ER-118耦合网络三者信息侧发生级联失效时连通能力变化情况,纵轴为R信息网连通能力,横轴k为发生故障传播的次数,能直观表现故障发生过程中的网络连通性能。图中表明,WS-118耦合网络和ER-118耦合网络在面对随机节点攻击和高度数节点攻击时,其信息侧都表现出差于BA-118
图3
耦合网络信息侧的鲁棒性,故障传播速度快。对于WS-118耦合网络和ER-118耦合网络来说,在故障传播初期,信息网的连通性能下降较缓慢,遭到破坏的节点数较少;故障传播中期,网络连通性能出现骤降的情况,大量节点被移除;在传播次数达到6至7次时,网络出现奔溃现象。BA-118耦合网络在随机节点攻击模式和高度数节点攻击模式下,其信息网都表现出较强的鲁棒性。在故障传播期间,网络连通性骤降情况不明显,故障传播速度较慢。这反映了当初始故障发生在信息网时,由于网络的耦合作用,网络分布更均匀的电力网更容易出现成片的故障节点,所以电力网由小世界网络和随机网络生成的耦合网络发生级联失效时其信息侧鲁棒性较弱,反而是由无标度网络生成的电力网与具有小世界网络特性的信息网耦合在抵御级联失效时有更强的鲁棒性。
5.3 保护策略及其网络鲁棒性分析
本节对三种耦合网络单侧电力网的结构特点进行分析,针对其结构特点研究基于介数删边策略、保护高介数节点策略和基于最短路径加边策略三种保护对单侧信息网鲁棒性的影响。
5.3.1 保护策略
(1) 基于介数删边策略(Betweenness deletion edges strategy,BDES)
对WS-118耦合网络而言,其单侧电力网为小世界网络,小世界网络是一类具有较短平均路径长度和较高聚类系数的网络模型,网络节点聚集程度较高,其节点介数差异性较大,介数高的节点收到的负载多,容易出现过载而失效,因此考虑通过删除网络中介数大的节点的以降低网络介数差异性。
具体策略如下:对网络的每个节点进行初始化介数计算并排序,以介数最大的节点及其相邻节点中介数最大的点为节点对,对该节点对的连接边进行删除。重复上述方法直到删边数达到N条。
(2) 保护高介数节点策略(High-betweenness node protecting strategy,HNPS)
BA-118耦合网络单侧电力网为无标度网络,无标度网络中度分布与介数分布是呈正相关的,其介数分布同度分布一样,网络中高介数节点和低介数节点相差很大。度数体现网络中节点的连接特征,而节点介数表示网络中所有节点对之间通过该节点的最短路径的条数,体现了网络中的负载特征,介数高的节点一旦失效,自身负载通过路径进行传播对网络整体负载水平影响较大,因此考虑对BA-118耦合网络信息侧进行高介数节点保护。
具体策略如下:对网络的每个节点进行初始化介数计算并排序,选择前N个高介数节点进行保护,视被保护的节点在遭受攻击时仍可以正常工作。
(3) 基于最短路径加边策略(Shortest-path addition edges strategy,SAES)
ER-118耦合网络单侧电力网为随机网络,网络中的中高度数节点相对多,但由于随机网络是由网络节点数和节点连接概率确定的,节点连接概率的存在使得随机网络结构具有随机性。而最短路径总是经过网络中度数较高的节点,考虑对网络中最短路径的节点进行加边以分担高度数节点的负载。
具体策略如下:对网络的每个节点进行初始化最短路径计算并排序,在最短路径值最大的两个节点之间加边。重复上述方法直到加边数达到N条。
5.3.2 应用保护策略后网络鲁棒性分析
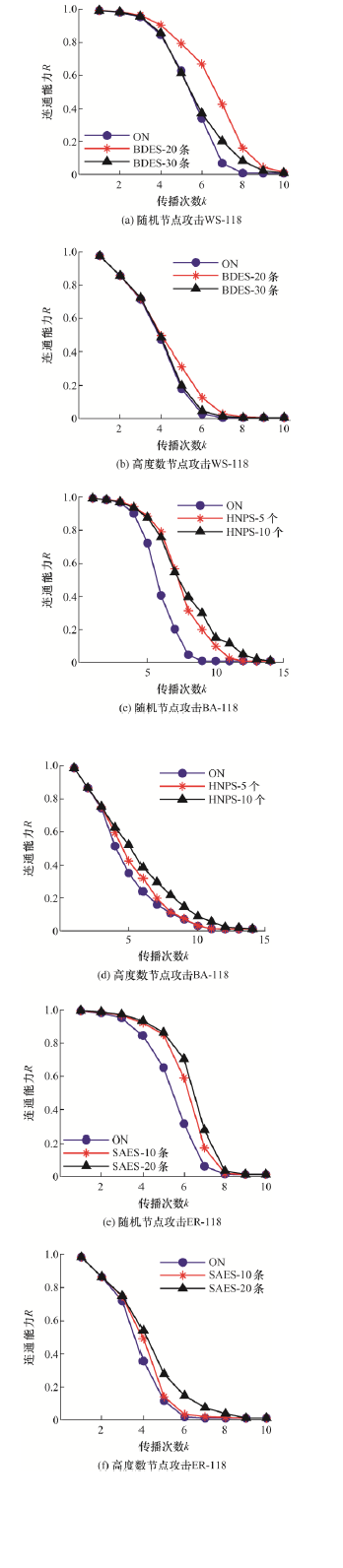
图4为增加保护策略后的网络与没有增加保护
图4
策略的原网络(Original network,ON)在面对随机节点攻击和高度数节点攻击的鲁棒性对比情况。图4a和图4b分别为随机节点攻击和高度数节点攻击下WS-118耦合网络电力网在增加BDES前后的信息网鲁棒性对比情况,试验选取删边为20条和30条的保护策略与原网络进行对比,删边策略在提高网络鲁棒性的同时也可能影响到网络的整体结构,删边数越多对网络的破坏程度越大。图4c和图4d分别为随机节点攻击和高度数节点攻击下BA-118耦合网络电力网在增加HNPS前后的信息网鲁棒性对比情况,试验选取保护高介数节点数为5个和10个与原网络进行对比。图4e和图4f分别为随机节点攻击和高度数节点攻击下ER-118耦合网络电力网在增加SAES前后的信息网鲁棒性对比情况,试验选取增加网络边数为10条和20条与原网络进行对比。从图4中可以看出,针对每种保护策略进行的两组试验都能提高网络在面对攻击时的鲁棒性。增加保护策略后的网络在遭受攻击时,信息网连通性在随故障传播过程中的总体趋势不会有过大变化,故障传播初期信息网内遭破坏节点一样不多,网络连通性下降缓慢,故障传播中期及后期,网络连通能力明显有所提高,并且网络在完全崩溃较原始网络慢,故障传播速度有所减缓。由于鲁棒性分析针对的是耦合网络单侧信息网,保护策略仅应用于耦合网络单侧电力网,而单侧信息网遭受攻击后的网络连通能力不仅受到单侧电力网网络结构的影响,还与网络交互相关,因此增加保护策略后的网络鲁棒性出现在总体趋势无过大变化的前提下,在故障传播过程有所提高的情况。根据单侧电力网结构特性提出的保护策略能在一定程度上提高耦合网络信息侧的鲁棒性。
6 结论
本文构建了三种含不同子网络的两层电力信息耦合网络模型,对基于过载机理的耦合网络发生级联失效时的交互机理进行研究,分析耦合网络单侧信息网在遭受攻击时,耦合网络单侧电力网结构特性对单侧信息网鲁棒性的影响,最后对网络的结构特点进行分析,从而提出对相应耦合网络提出保护策略以提高网络鲁棒性。研究得出以下结论,BA-118耦合网络在随机节点攻击模式和高度数节点攻击模式下,其信息网都表现出较强的鲁棒性。电力网为无标度网络的子网络与具有小世界特性的信息网进行耦合,相比较电力网为小世界网络和随机网络的子网络,在抵御级联失效时有更强的鲁棒性。此外,针对耦合网络单侧电力网结构特性而提出的保护策略,能在故障传播过程中提高耦合信息网的鲁棒性。上述结果在构建具有强鲁棒性的耦合网络有一定的参考意义。
本文的研究方法主要考虑电力网和信息网的拓扑结构特性和负载因素,忽略了电力网的运行潮流特性和信息网的通信业务特性,在反映网络交互的动态发展过程和构建网络模型上还存在不足,具有一定的局限性。下一步的研究重点将同时考虑电力网的运行特性和信息网的传输特性,建立更加符合实际的网络模型,深入研究耦合网络间的交互机理,更加准确地评估耦合网络的性能。
参考文献
电力信息物理融合系统的建模分析与控制研究框架
[J].传统的电力系统研究与信息系统研究在理论和方法上基本都是割裂的,故在现有的理论和方法框架下难以系统而深入地分析信息系统对电力系统分析与控制的影响。实现智能电网的关键之一就在于怎样将前沿的计算、通信、传感技术与电力系统紧密而有机地结合起来,而信息物理融合系统(CPS)的目标正是将物理系统和信息系统融合为新型工业系统。在此背景下,将CPS概念与电力系统特点相结合,提出电力CPS架构;利用微分代数方程组、有穷自动机、随机过程、排队论等数学工具,建立其稳态与动态模型,阐述相应的分析方法,并进一步提出电力CPS可靠性和安全性研究方向。最后,基于网络延时和丢失补偿提出了多种控制方法相结合的混合控制策略。
Modeling analysis and control research framework of cyber physical power systems
[J].
由乌克兰停电事件看信息能源系统综合安全评估
[J].
Comprehensive security assessment for a cyber physical energy system:A lesson from Ukraine’s blackout
[J].
Catastrophic cascade of failures in interdependent networks
[J].
DOI:10.1038/nature08932
URL
PMID:20393559
[本文引用: 2]

Complex networks have been studied intensively for a decade, but research still focuses on the limited case of a single, non-interacting network. Modern systems are coupled together and therefore should be modelled as interdependent networks. A fundamental property of interdependent networks is that failure of nodes in one network may lead to failure of dependent nodes in other networks. This may happen recursively and can lead to a cascade of failures. In fact, a failure of a very small fraction of nodes in one network may lead to the complete fragmentation of a system of several interdependent networks. A dramatic real-world example of a cascade of failures ('concurrent malfunction') is the electrical blackout that affected much of Italy on 28 September 2003: the shutdown of power stations directly led to the failure of nodes in the Internet communication network, which in turn caused further breakdown of power stations. Here we develop a framework for understanding the robustness of interacting networks subject to such cascading failures. We present exact analytical solutions for the critical fraction of nodes that, on removal, will lead to a failure cascade and to a complete fragmentation of two interdependent networks. Surprisingly, a broader degree distribution increases the vulnerability of interdependent networks to random failure, which is opposite to how a single network behaves. Our findings highlight the need to consider interdependent network properties in designing robust networks.
相依网络理论及其在电力信息-物理系统结构脆弱性分析中的应用综述
[J].
Review on interdependent networks theory and its applications in the structural vulnerability analysis of electrical cyber-physical system
[J].
多层复杂网络理论研究进展:概念、理论和数据
[J].
Research progress of multi-layer complex network theory:Concept,theory and data
[J].
电力信息-物理相互依存网络脆弱性评估及加边保护策略
[J].
Vulnerability evaluation and link addition protection strategy research of electrical cyber-physical interdependent networks
[J].
不同耦合方式和耦合强度对电力-通信耦合网络的影响
[J].
Influences of various coupled patterns and coupling strength on power-communication coupled networks
[J].
Cascading effects in interdependent networks
[J].Modern systems are increasingly dependent upon and interacting with each other, and become interdependent networks. These interdependent networks may exhibit some interesting and even surprising behaviors due to the interdependency and the interplay between the constituent systems. In this article we focus on two important phenomena, namely cascading failure in cyber-physical systems (CPS) and information cascade in coupled social networks. Specifically, cascading failures may occur in CPS that exhibit functional interdependency between two constituent systems (e.g. smart grid); information cascade may happen in multiple social networks that are coupled together by so-called multi-membership individuals. This article explores these two types of cascading effects in interdependent networks by reviewing existing studies in the literature. We review different models in the literature to study the two types of cascading effects in interdependent networks, and highlight the key findings from these studies.
相依网络在不同攻击策略下的鲁棒性
[J].
Robustness of interdependent networks under several intentional attack strategies
[J].
Robustness of interdependent networks under targeted attack
[J].DOI:10.1103/PhysRevE.83.065101 URL [本文引用: 1]
Comparison of cascading failures between power information interdependent networks and single-layer power grids
[J].
The robustness of interdependent transportation networks under targeted attack
[J].DOI:10.1209/0295-5075/103/68005 URL [本文引用: 1]
基于不同子网络级联机制的相依网络鲁棒性研究
[J].
Robustness of interdependent networks based on different subnet cascade mechanisms
[J].
Attack robustness of cascading load model in interdependent networks
[J].DOI:10.1142/S0129183115500308 URL [本文引用: 1]
Robustness of interdependent power grids and communication networks:A complex network perspective
[J].
复杂网络理论在电力CPS级联失效研究中的应用综述
[J].
Survey of cascading failures in cyber physical power system based on complex network theory
[J].
复杂网络基础理论
[M].
The basic theory of complex networks
[M].
基于改进渗流理论的信息物理融合电力系统连锁故障模型
[J].
Model cascading failures in cyber physical power system based on improved percolation theory
[J].
Collective dynamics of small world networks
[J].
DOI:10.1038/30918
URL
PMID:9623998
[本文引用: 1]

Networks of coupled dynamical systems have been used to model biological oscillators, Josephson junction arrays, excitable media, neural networks, spatial games, genetic control networks and many other self-organizing systems. Ordinarily, the connection topology is assumed to be either completely regular or completely random. But many biological, technological and social networks lie somewhere between these two extremes. Here we explore simple models of networks that can be tuned through this middle ground: regular networks 'rewired' to introduce increasing amounts of disorder. We find that these systems can be highly clustered, like regular lattices, yet have small characteristic path lengths, like random graphs. We call them 'small-world' networks, by analogy with the small-world phenomenon (popularly known as six degrees of separation. The neural network of the worm Caenorhabditis elegans, the power grid of the western United States, and the collaboration graph of film actors are shown to be small-world networks. Models of dynamical systems with small-world coupling display enhanced signal-propagation speed, computational power, and synchronizability. In particular, infectious diseases spread more easily in small-world networks than in regular lattices.
Emergence of scaling in random networks
[J].
DOI:10.1126/science.286.5439.509
URL
PMID:10521342
[本文引用: 1]

Systems as diverse as genetic networks or the World Wide Web are best described as networks with complex topology. A common property of many large networks is that the vertex connectivities follow a scale-free power-law distribution. This feature was found to be a consequence of two generic mechanisms: (i) networks expand continuously by the addition of new vertices, and (ii) new vertices attach preferentially to sites that are already well connected. A model based on these two ingredients reproduces the observed stationary scale-free distributions, which indicates that the development of large networks is governed by robust self-organizing phenomena that go beyond the particulars of the individual systems.
电力系统复杂网络特性分析与模型改进
[J].
Complex network characteristic analysis and model improving of the power system
[J].