1 引言
随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] 。但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] 。含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] 。所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] 。
针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义。文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值。文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化。文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏。文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响。文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂。
对此,本课题在充分考虑分布式电源出力波动性和负荷不确定性的基础上,建立了以系统有功网损和电压偏移量最小为多目标的配电网概率无功优化模型。采用两点估计法用于风机出力、光伏出力和负荷概率潮流的计算,同时结合IPSO算法求解目标函数的最优值。然后以改进的IEEE33节点配电系统为算例进行仿真测试,其结果表明该优化配置模型可以改善系统性能,保证系统能够安全稳定地运行,也说明了模型求解算法的可行性及快速有效性。
2 分布式电源和负荷功率概率模型
2.1 风力发电的出力概率模型
风速$v$是根据天气情况而不断变化的,历史研究数据表明,威布尔(Weibull)分布[10 ,11 ] 对风速进行的统计描述较为准确,则风速的概率密度函数为
(1) $f(v)=\frac{K}{C}{{\left( \frac{v}{C} \right)}^{K-1}}\exp \left( -{{\left( \frac{v}{C} \right)}^{K}} \right)$
式中,$K$和$C$分别为Weibull分布的形状参数和尺度参数。其值可由式(2)获得
(2) $\left\{ \begin{align} & K={{\left( \frac{{{\sigma }_{v}}}{{{\mu }_{v}}} \right)}^{-1.086}} \\ & C=\frac{{{\mu }_{v}}}{\Gamma (1+1/K)} \\ \end{align} \right.$
式中,$\Gamma $为Gamma函数;${{\sigma }_{v}}$和${{\mu }_{v}}$分别表示风速的方差和期望,其值根据风速的统计数据可得到。
风电场的出力是有关风速的函数,所以风电场输出功率的随机性主要取决于风速的随机性,则风机输出的有功功率${{P}_{\text{w}}}$为
(3) ${{P}_{\text{w}}}=\left\{ \begin{align} & 0 v<{{v}_{\text{ci}}}\ \ \ \ v>{{v}_{\text{co}}} \\ & {{P}_{\text{r}}}\frac{v-{{v}_{\text{ci}}}}{{{v}_{\text{r}}}-{{v}_{\text{ci}}}}\ \ \ \ {{v}_{\text{ci}}}<v<{{v}_{\text{r}}} \\ & {{P}_{\text{r}}} {{v}_{\text{r}}}<v<{{v}_{\text{co}}} \\ \end{align} \right.$
式中,${{P}_{\text{r}}}$、${{v}_{\text{r}}}$分别为风机的额定功率和额定风速;${{v}_{\text{ci}}}$、${{v}_{\text{co}}}$分别为风机的切入和切出风速。
恒速异步发电机是目前风力发电最常用的一种,在向电网中发送有功的同时吸收无功,设风机以恒功率因数的方式运行,则风机输出的无功功率为
(4) ${{Q}_{\text{W}}}=-{{P}_{\text{w}}}\tan (\arccos {{\varphi }_{\text{W}}})$
式中,${\varphi }_{\text{W}}$为风电机组的功率因数角。
2.2 光伏发电的出力概率模型
一般认为太阳光照强度$r$近似服从 Beta 分布[12 ,13 ] ,即
(5) $f\left( r \right)=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{{\left( \frac{r}{{{r}_{\max }}} \right)}^{\alpha -1}}{{\left( 1-\frac{r}{{{r}_{\max }}} \right)}^{\beta -1}}$
式中,$\alpha $、$\beta $为Beta分布的形状参数;$r$和${{r}_{\max }}$分别为某一时段内的实际光照强度和最大光照强度。
对于一个太阳能阵列,光伏电源输出功率${{P}_{\text{PV}}}$和太阳能光照强度$r$之间存在如下函数关系
(6) ${{P}_{\text{PV}}}=rA\eta$
式中,$A$为太阳能电池阵列的总面积;$\eta $为太阳能电池阵列的光电转换效率。
(7) $\left\{ \begin{align} & f({{P}_{\text{PV}}})=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}{{\left( \frac{{{P}_{\text{PV}}}}{{{P}_{\text{PV,max}}}} \right)}^{\alpha -1}}{{\left( 1-\frac{{{P}_{\text{PV}}}}{{{P}_{\text{PV,max}}}} \right)}^{\beta -1}} \\ & {{Q}_{\text{PV}}}={{P}_{\text{PV}}}\tan ({{\varphi }_{\text{PV}}}) \\ \end{align} \right.$
式中,${{P}_{\text{PV}}}$、${{Q}_{\text{PV}}}$分别为光伏发电机组输出的有功、无功功率;${{\varphi }_{\text{PV}}}$为光伏发电机组的功率因数角;${{P}_{\text{PV,max}}}$为最大有功输出。
2.3 负荷功率的概率模型
一般认为基于预测的负荷功率具有正态分布[14 ,15 ] ,则负荷功率的概率密度函数可表示为
(8) $\left\{ \begin{align} & f\left( P \right)=\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}{{\sigma }_{P}}}\exp \left( -\frac{{{\left( P-{{\mu }_{P}} \right)}^{2}}}{2\sigma _{P}^{2}} \right) \\ & f\left( Q \right)=\frac{1}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }}{{\sigma }_{Q}}}\exp \left( -\frac{{{\left( Q-{{\mu }_{Q}} \right)}^{2}}}{2\sigma _{Q}^{2}} \right) \\ \end{align} \right.$
式中,$P$、$Q$分别为负荷的有功功率和无功功率;${{\mu }_{P}}$、${{\sigma }_{P}}$分别为负荷有功功率的期望值和方差;${{\mu }_{Q}}$、${{\sigma }_{Q}}$分别为负荷无功功率的期望值和方差。
3 含DG的配电网无功优化模型
3.1 目标函数
本文综合考虑电网运行的经济性和安全性,以系统有功损耗${{P}_{\text{loss}}}$和节点电压偏移量$\text{d}U$最小为目标,建立了含DG的配电网无功优化数学模型。
(9) $\min {{f}_{1}}={{P}_{\text{loss}}}=\sum\limits_{i,j\subset {{N}_{\text{B}}}}{{{G}_{ij}}(U_{i}^{2}+U_{j}^{2}-2{{U}_{i}}{{U}_{j}}\cos {{\theta }_{ij}})}$
式中,${{N}_{\text{B}}}$为支路数总数;${{G}_{ij}}$、${{\theta }_{ij}}$分别为节点i 和j 之间的电导、电压相角差;${{U}_{i}}$、${{U}_{j}}$分别为负荷节点i 和j 的电压幅值。
(10) $\min {{f}_{2}}=\text{d}U={{\sum\limits_{i}^{{{N}_{\text{L}}}}{\left( \frac{{{U}_{i}}-U_{i}^{\text{spec}}}{\Delta U_{\text{L}}^{\max }} \right)}}^{2}}\Delta U_{\text{L}}^{\max }$
式中,$U_{i}^{\text{spec}}$为期望电压,通常设为1.0 p.u.;$\Delta U_{\text{L}}^{\max }=U_{i}^{\max }-U_{i}^{\min }$为最大允许电压偏差;${{N}_{\text{L}}}$为系统的负荷节点数。
综合以上两个方面,引入电压越限惩罚函数${{W}_{\text{V}}}$,作为对未能满足各节点电压约束条件的一种惩罚。则无功优化的目标函数可表示为
(11) $\begin{matrix} F={{P}_{\text{loss}}}+\text{d}U+{{W}_{\text{V}}}= {{\lambda }_{1}}{{f}_{1}}+{{\lambda }_{2}}{{f}_{2}}+\gamma \sum\limits_{i=1}^{n}{{{\left( \frac{\Delta {{U}_{i}}}{{{U}_{i,\max }}-{{U}_{i,\min }}} \right)}^{2}}} \\ \end{matrix}$
(12) $\Delta {{U}_{i}}=\left\{ \begin{align} & {{U}_{i}}-{{U}_{i,\max }} {{U}_{i}}>{{U}_{i,\max }} \\ & 0 \ \ {{U}_{i,\min }}\le {{U}_{i}}\le {{U}_{i,\max }} \\ & {{U}_{i,\min }}-{{U}_{i}} {{U}_{i}}<{{U}_{i,\min }} \\ \end{align} \right.$
式中,${{\lambda }_{1}}$、${{\lambda }_{2}}$为反映系统运行经济性和电压稳定性偏好的权重因子,也称偏好因子,且${{\lambda }_{1}}+{{\lambda }_{2}}=1$;$\gamma $为电压越限惩罚系数;${{U}_{i,\max }}$、${{U}_{i,\min }}$分别为节点i 的电压上下限。
3.2 约束条件
(13) $\left\{ \begin{align} & {{P}_{\text{G},i}}={{P}_{\text{L},i}}+{{U}_{i}}\sum\limits_{j=1}^{{{N}_{\text{B}}}}{{{U}_{j}}({{G}_{ij}}\cos {{\theta }_{ij}}+{{B}_{ij}}\sin {{\theta }_{ij}})} \\ & {{Q}_{\text{G},i}}={{Q}_{\text{L},i}}+{{U}_{i}}\sum\limits_{j=1}^{{{N}_{\text{B}}}}{{{U}_{j}}({{G}_{ij}}\sin {{\theta }_{ij}}-{{B}_{ij}}\cos {{\theta }_{ij}})} \\ \end{align} \right.$
式中,${{P}_{\text{G},i}}$、${{P}_{\text{L},i}}$分别表示节点i 处发电机和负荷的有功功率;${{B}_{ij}}$为节点i 和j 之间的电纳;${{Q}_{\text{G},i}}$、${{Q}_{\text{L},i}}$表示节点$i$处发电机和负荷的无功功率。
(14) $\left\{ \begin{align} & {{U}_{i,\min }}\le {{U}_{i}}\le {{U}_{i,\max }} \\ & {{T}_{\min }}\le T\le {{T}_{\max }} \\ & {{Q}_{{{C}_{i}},\min }}\le {{Q}_{{{C}_{i}}}}\le {{Q}_{{{C}_{i}},\max }} \\ & {{K}_{{{C}_{i}}}}\le {{K}_{{{C}_{i}},\max }} \\ & {{P}_{\text{DG},\min }}<{{P}_{\text{DG},i}}\le {{P}_{\text{DG,max}}} \\ \end{align} \right.$
式中,$T$和${{T}_{\max }}$、${{T}_{\min }}$分别为有载调压变压器的档位和档位上下限;${{Q}_{{{C}_{i}}}}$和${{Q}_{{{C}_{i}},\max }}$、${{Q}_{{{C}_{i}},\min }}$分别为节点i 所装设的SVG容量和容量上下限;${{K}_{{{C}_{i}}}}$、${{K}_{{{C}_{i}},\max }}$分别为补偿电容器i 在1组中投切的次数和最大次数;${{P}_{\text{DG},i}}$和${{P}_{\text{DG},\max }}$、${{P}_{\text{DG},\min }}$分别为节点i 处DG的接入容量和容量上下限。
4 模型的求解
4.1 基于两点估计法的概率潮流计算
两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值。由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算。
(15) $X={{[{{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}}]}^{\text{T}}}$
系统的有功损耗和节点电压偏移表示为节点注入量的函数
(16) $\left\{ \begin{align} & {{P}_{\text{L}}}={{F}_{1}}({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}}) \\ & \text{d}U={{F}_{2}}({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}}) \\ \end{align} \right.$
通过使用均值$aver\_{{x}_{i}}$两侧的两个变量${{x}_{i1}}$和${{x}_{i2}}$来匹配随机量${{x}_{i}}$的前三阶矩,以取代该节点注入量的概率密度函数,计算过程详见文献[16 ]。则对某一节点随机变量${{x}_{i}}$用2×n 组数据进行确定性潮流计算
(17) $\begin{matrix} \left\{ \begin{align} & (aver\_{{x}_{1}},aver\_{{x}_{2}},\cdots ,{{x}_{i1}},aver\_{{x}_{n-1}},aver\_{{x}_{n}}) \\ & (aver\_{{x}_{1}},aver\_{{x}_{2}},\cdots ,{{x}_{i2}},aver\_{{x}_{n-1}},aver\_{{x}_{n}}) \\ \end{align} \right. \\ i=1,2,\cdots ,n \\ \end{matrix}$
可得系统有功损耗和节点电压偏差的两个估计值${{P}_{\text{L}}}(i,1)$,${{P}_{\text{L}}}(i,2)$和$\text{d}U(i,1)$,$\text{d}U(i,2)$。则配电网的系统有功损耗和节点电压偏差可通过式(18)求解
(18) $\left\{ \begin{align} & {{P}_{\text{L}}}=\sum\limits_{i=1}^{n}{[{{\omega }_{i,1}}\times {{P}_{\text{L}}}(i,1)+{{\omega }_{i,2}}\times {{P}_{\text{L}}}(i,2)]} \\ & \text{d}U=\sum\limits_{i=1}^{n}{[{{\omega }_{i,1}}\times \text{d}U(i,1)+{{\omega }_{i,2}}\times \text{d}U(i,2)]} \\ \end{align} \right.$
4.2 改进的粒子群优化算法
粒子群算法以其简单、易实现等突出特点在离散型数学模型的求解中应用最为广泛[19 ,20 ] 。可是在标准粒子群算法的使用中,惯性权重和学习因子通常被取为常数,在参数恒定的情况下,算法在后期迭代寻优过程中易陷入局部最优,造成早熟的现象。所以,为保持迭代过程中粒子的多样性,需要对参数进行改进从而克服算法出现局部最优解的缺陷,使算法在迭代前期具有较强的全局搜索能力,提高种群多样性,而在后期具有更强的局部搜索能力,提高寻优精度和速度。
惯性权重$\omega $表示粒子当前速度对先前速度的继承能力,控制其取值大小可影响粒子的搜索能力。大量研究表明,$\omega $较大时有利于全局搜索,$\omega $较小时则有利于局部搜索。因此使惯性权重做线性递减,最终对$\omega $的改进如下
(19) $\omega ={{\omega }_{\max }}-({{\omega }_{\max }}-{{\omega }_{\min }})\frac{k}{{{k}_{\max }}}$
式中,${{\omega }_{\max }}$、${{\omega }_{\min }}$分别为$\omega $的最大值和最小值,一般分别取0.9和0.4;$k$、${{k}_{\max }}$分别为当前迭代次数和最大迭代次数。
学习因子${{c}_{1}}$、${{c}_{2}}$在整个寻优过程中起到调整粒子自身个体极值和全局极值的作用。为提高搜索效率和精度,使学习因子在迭代初期满足${{c}_{1}}>{{c}_{2}}$,以提高全局搜索能力;而在迭代后期满足${{c}_{2}}>{{c}_{1}}$,以提高局部搜索能力。最终对${{c}_{1}}$、${{c}_{2}}$的改进如下
(20) $\left\{ \begin{align} & {{c}_{1}}={{c}_{1,\max }}+({{c}_{1,\min }}-{{c}_{1,\max }})\frac{k}{{{k}_{\max }}} \\ & {{c}_{2}}={{c}_{2,\min }}+({{c}_{2,\max }}-{{c}_{2,\min }})\frac{k}{{{k}_{\max }}} \\ \end{align} \right.$
式中,${{c}_{1,\max }}$、${{c}_{1,\min }}$分别为${{c}_{1}}$的上下限;${{c}_{2,\max }}$、${{c}_{2,\min }}$分别为${{c}_{2}}$的上下限。一般取${{c}_{1,\min }}$=${{c}_{2,\min }}$=0.5,${{c}_{1,\max }}$=${{c}_{2,\max }}$=2.5。
(21) $v_{id}^{k+1}=\omega v_{id}^{k}+{{c}_{1}}{{r}_{1}}(p_{\text{bes}{{\text{t}}_{id}}}^{k}-x_{id}^{k})+{{c}_{2}}{{r}_{2}}(g_{\text{bes}{{\text{t}}_{d}}}^{k}-x_{id}^{k})$
(22) $x_{id}^{k+1}=x_{id}^{k}+v_{id}^{k+1}$
式中,$i=1,2,\cdots ,n$为群体中粒子的数量;$d$为粒子的维度;${{v}_{i}}$、${{x}_{i}}$分别为第$i$个粒子的当前速度和位置;${{r}_{1}}$、${{r}_{2}}$是0~1之间均匀分布的随机数;${{p}_{\text{bes}{{\text{t}}_{i}}}}$是第$i$个粒子的个体最优解;${{g}_{\text{best}}}$是全局最优解。
4.3 模型求解的步骤
(1) 初始化。设定原始测试线路的数据,设置种群粒子的总数和最大迭代次数,并初始化各粒子的速度和位置。
(2) 采用两点估计法对种群中粒子的概率潮流进行确定性潮流计算,得到有功网损和电压偏移。
(3) 通过目标函数式(11)求出种群中每个粒子的适应度值,然后通过比较确定出粒子个体最优和群体最优,分别赋值于${{p}_{\text{bes}{{\text{t}}_{i}}}}$和${{g}_{\text{best}}}$。
(4) 更新迭代次数,然后根据式(19)、(20)对惯性权重和学习因子进行相应的更新计算,按照式 (21)、(22)对种群中每个粒子的速度和位置进行 更新。
(5) 根据式(11)对每个粒子的适应度值重新进行计算,将适应度值与历史最优解进行比较,重新确定出粒子个体最优和群体最优,然后更新${{p}_{\text{bes}{{\text{t}}_{i}}}}$和${{g}_{\text{best}}}$。
(6) 重复步骤(4)~(5),直到满足收敛条件或达到最大迭代次数时,停止迭代并输出结果。
5 算例分析
5.1 系统参数
本文采用改进的IEEE33节点配电系统进行仿真测试,并通过Matlab软件进行编程实现。系统的原始数据详见文献[21 ]。
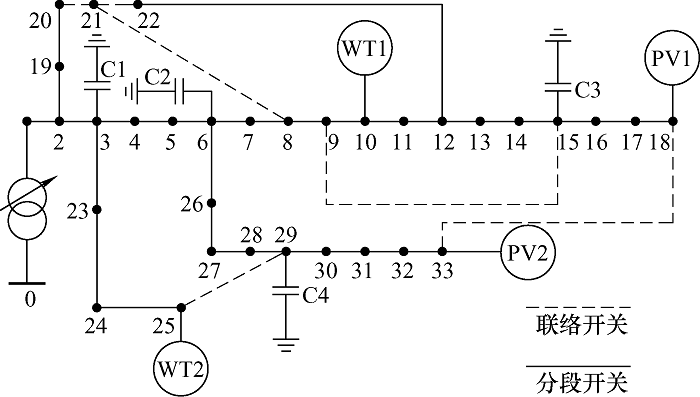
在此系统中,基准电压为12.66 kV,基准功率为10 MVA,系统中节点电压的允许范围为额定电压的±5%。在0~1节点间连接档位为8、调节范围为±4×1.25%的有载调压变压器;在节点3、6、15和29处分别接入无功容量为100 kVar的10组可投切电容器组;在节点10、25处并入额定容量均为400 kW的风电系统,Weibull分布的参数$K=8.5$、$C=2.0$;在节点18、33处并入额定容量均为600 kW的光伏系统,Beta分布的形状参数$\alpha =0.58$、$\beta =1.51$。风电和光伏系统都采用恒定功率因数的工作方式进行,固定功率因数为0.95(滞后);权重因子${{\lambda }_{1}}=0.6$,${{\lambda }_{2}}=0.4$。具体接入如图1 所示。IPSO算法参数设置如下:种群数为50,最大迭代次数为100。
图1
5.2 优化效果测试
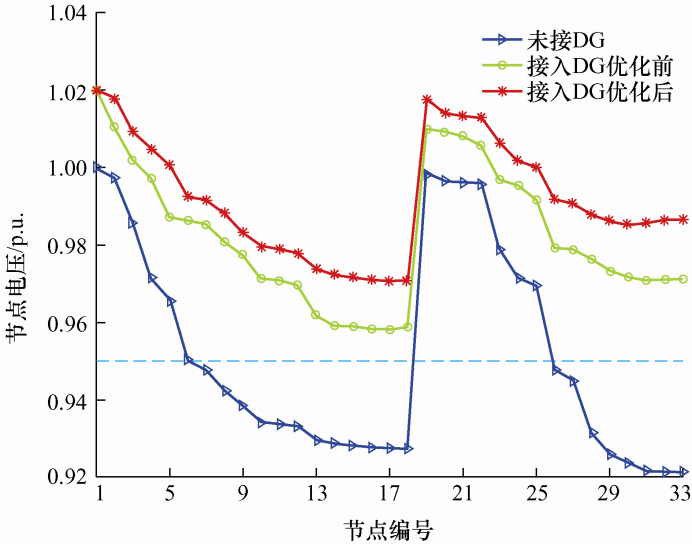
为验证本文所建优化模型的有效性,分别对未接入DG和接入DG的IEEE33节点系统进行仿真测试。系统优化前后的控制变量参数、优化结果和各节点电压分别如表1 、表2 和图2 所示。
图2
由表2 和图2 可知,较DG并网前,系统有功网损下降至130.08 kW,减少了19.06%,电压偏移下降至1.130 3 p.u.,减少了12.19%,可见DG的接入有利于系统经济性和安全性的提高。在采用IPSO算法对配电网进行无功优化后,系统有功网损和电压偏移进一步下降,分别减少了52.97%和51.50%。同时,从表1 可看出,较优化前,离散型控制设备的投入容量也明显减少,节省了对配电网进行无功优化时所需的无功补偿的设备投资。综上所述,本文所建优化模型和求解算法能达到降低系统网损和电压偏移的目的,从而保证系统运行的经济性和安全性。
5.3 算法性能测试
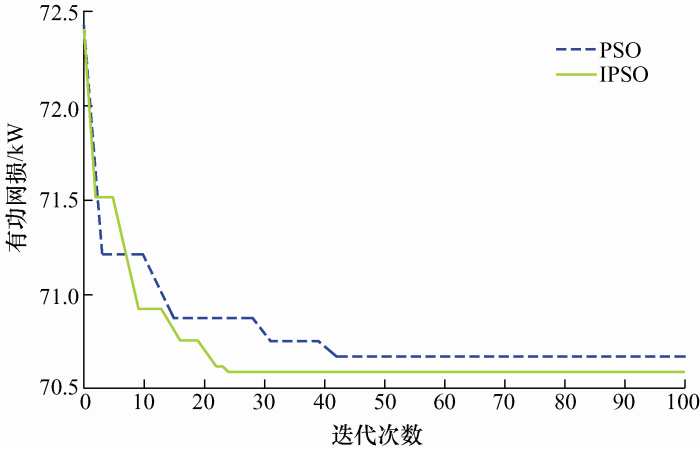
为验证IPSO算法的快速有效性,与传统PSO算法进行比较。分别对接入分布式电源和负荷的IEEE33节点系统进行测试,其中传统PSO算法的学习因子${{c}_{1}}$=${{c}_{2}}$=2,惯性权重$\omega $=0.5;IPSO算法的$\omega $和${{c}_{1}}$、${{c}_{2}}$分别按式(22)、(23)进行计算。两种算法的收敛特性曲线如图3 所示。
图3
由图3 可看出,IPSO算法在迭代到第25次时就已接近最小值,而PSO算法直到第41次迭代时才接近最优解,可知,IPSO算法降低系统网络损耗的能力明显比传统PSO算法好。这说明对PSO算法中的惯性权重和学习因子进行改进后,算法的搜索能力得到加强,收敛速度得到加快,从而能够有效克服粒子群算法早熟收敛的缺陷,使寻优值更精确。
6 结论
本文对所建模型和算法进行系统测试分析后得到以下两个结论。
(1) 充分考虑了多种分布式电源出力随机性以及负荷不确定性对配电网的影响,建立了配电网的多目标概率无功优化数学模型。对配电网进行无功优化后,系统网损和电压偏移量都减小了,系统整体性能得到优化。
(2) 结合两点估计法和IPSO算法对所建模型进行求解,不但提高了运算效率,而且验证了IPSO算法的可行性及有效性。说明该优化配置模型可以达到降低网络损耗、提高节点电压质量的目的。
参考文献
View Option
[1]
晏浩然 , 吴杰康 , 晏寒婷 , 等 . 新能源配电网低碳高效运行的可拓层次评估方法
[J]. 电气工程学报 , 2018 ,31 (2 ):15 -23 .
[本文引用: 1]
YAN Haoran WU Jiekang YAN Hanting , et al . Extension hierarchy analytical method for low-carbon and high-efficiency operation of distribution grids with renewable energy
[J]. Journal of Electrical Engineering , 2018 ,31 (2 ):15 -23 .
[本文引用: 1]
[2]
谢海波 , 武小梅 , 林翔 , 等 . 含分布式电源的配电网无功优化研究综述
[J]. 广东电力 , 2017 ,30 (2 ):102 -109 .
[本文引用: 1]
XIE Haibo WU Xiaomei LIN Xiang , et al . Review on reactive power optimization of distribution network with distributed power supply
[J]. Guangdong Electric Power , 2017 ,30 (2 ):102 -109 .
[本文引用: 1]
[3]
訾振宁 , 何永君 , 赵东元 , 等 . 新一代电力系统灵活柔性特征研究
[J]. 电气工程学报 , 2019 ,14 (3 ):1 -8 .
DOI:10.11985/2019.03.001
URL
[本文引用: 1]
电力系统转型是能源革命的必然需要;电力系统转型是保证能源转型核心指标能够实现的关键;电力系统的灵活柔性是新一代电力系统的显著特征,并且获得了国内外学者的广泛认同。针对电力系统在“源-网-荷”三个环节的灵活柔性进行了技术层面的需求分析,凝练识别出新一代电力系统灵活柔性特征关键技术,并对这些关键技术的发展进行了简要阐述和发展展望研究。研究结果表明,通过大量灵活柔性技术的研究和相关工程的建设,将极大推动电力系统自身的创新、协调、绿色、开放、共享发展,进而助力能源革命。
ZI Zhenning HE Yongjun ZHAO Dongyuan , et al . Research on flexibility of new generation power system
[J]. Journal of Electrical Engineering , 2019 ,14 (3 ):1 -8 .
DOI:10.11985/2019.03.001
URL
[本文引用: 1]
电力系统转型是能源革命的必然需要;电力系统转型是保证能源转型核心指标能够实现的关键;电力系统的灵活柔性是新一代电力系统的显著特征,并且获得了国内外学者的广泛认同。针对电力系统在“源-网-荷”三个环节的灵活柔性进行了技术层面的需求分析,凝练识别出新一代电力系统灵活柔性特征关键技术,并对这些关键技术的发展进行了简要阐述和发展展望研究。研究结果表明,通过大量灵活柔性技术的研究和相关工程的建设,将极大推动电力系统自身的创新、协调、绿色、开放、共享发展,进而助力能源革命。
[4]
鲁裕婷 , 赵天乐 , 都洪基 , 等 . 基于改进粒子群算法的含DG配电网无功优化
[J]. 电力工程技术 , 2018 ,37 (6 ):69 -74 .
[本文引用: 1]
LU Yuting ZHAO Tianle DU Hongji , et al . Reactive power optimization of distribution network with distri- buted generation based on improved particle swarm opti- mization algorithm
[J]. Jiangsu Electrical Engineering , 2018 ,37 (6 ):69 -74 .
[本文引用: 1]
[5]
张丽 , 徐玉琴 , 王增平 , 等 . 包含分布式电源的配电网无功优化
[J]. 电工技术学报 , 2011 ,26 (3 ):168 -174 .
URL
[本文引用: 1]
将能够提供无功功率的分布式电源与传统的电压调节手段相结合, 研究了包含分布式电源的配电网无功优化问题。利用基于聚类和竞争克隆机制的多智能体免疫算法实现无功优化, 建立了无功优化问题的多智能体免疫模型。利用多智能体系统实现在寻优过程中动态改变抗原, 在亲和度成熟过程中引入聚类竞争克隆机制和混合变异算子, 以保存种群的多样性, 同时保证算法能够较快的收敛。通过改进的IEEE 33节点系统的仿真计算, 表明利用分布式电源对电网进行无功补偿能较大程度地降低系统有功损耗, 并且证明了所提算法的快速性和有效性。
ZHANG Li XU Yuqin WANG Zengping , et al . Reactive power optimization of distribution network including distributed power supply
[J]. Transactions of China Electrotechnical Society , 2011 ,26 (3 ):168 -174 .
URL
[本文引用: 1]
将能够提供无功功率的分布式电源与传统的电压调节手段相结合, 研究了包含分布式电源的配电网无功优化问题。利用基于聚类和竞争克隆机制的多智能体免疫算法实现无功优化, 建立了无功优化问题的多智能体免疫模型。利用多智能体系统实现在寻优过程中动态改变抗原, 在亲和度成熟过程中引入聚类竞争克隆机制和混合变异算子, 以保存种群的多样性, 同时保证算法能够较快的收敛。通过改进的IEEE 33节点系统的仿真计算, 表明利用分布式电源对电网进行无功补偿能较大程度地降低系统有功损耗, 并且证明了所提算法的快速性和有效性。
[6]
何禹清 , 彭建春 , 毛丽林 , 等 . 含多个风电机组的配电网无功优化
[J]. 电力系统自动化 , 2010 ,34 (19 ):37 -41 .
URL
[本文引用: 2]
风电机组出力的随机性使传统无功优化模型难以胜任。提出了含多个风电机组的配电网无功优化的模型和算法。基于场景分析法探讨了单台和多台不同参数风电机组的随机出力描述方法,并针对不同参数的风电机组同时接入系统时的情况,提出了系统场景的划分规则,继而建立了含多个风电机组的配电网无功优化的场景模型。针对多场景潮流计算的复杂性,提出一种高效算法,该算法先利用场景功率的相似性确定场景的分析次序,再将前一场景的潮流计算结果作为后一场景的初始条件,以加速潮流收敛。仿真结果验证了该模型和算法的有效性。
HE Yuqing PENG Jianchun MAO Lilin , et al . Reactive power optimization in distribution system with multiple wind power generators
[J]. Automation of Electric Power Systems , 2010 ,34 (19 ):37 -41 .
URL
[本文引用: 2]
风电机组出力的随机性使传统无功优化模型难以胜任。提出了含多个风电机组的配电网无功优化的模型和算法。基于场景分析法探讨了单台和多台不同参数风电机组的随机出力描述方法,并针对不同参数的风电机组同时接入系统时的情况,提出了系统场景的划分规则,继而建立了含多个风电机组的配电网无功优化的场景模型。针对多场景潮流计算的复杂性,提出一种高效算法,该算法先利用场景功率的相似性确定场景的分析次序,再将前一场景的潮流计算结果作为后一场景的初始条件,以加速潮流收敛。仿真结果验证了该模型和算法的有效性。
[7]
陈海焱 , 陈金富 , 段献忠 . 含风电机组的配网无功优化
[J]. 中国电机工程学报 , 2008 (7 ):40 -45 .
URL
[本文引用: 2]
研究了分布式电源中发展较为成熟的风力发电机组并网后配电网的无功优化问题,提出一种基于场景发生概率的无功优化综合指标,该指标由网损和静态电压稳定裕度两部分构成。基于该指标,提出一种新的无功优化模型。在该模型中,提出风电机组输出功率典型场景的选取策略,无功优化潮流计算中考虑了风电机组的特点,将其作为电压静特性节点处理。在求解方法上,采用基于自适应权重的遗传算法求解。算例表明,提出的模型和算法是可行的,对风电系统的运行具有一定的参考价值。
CHEN Haiyan CHEN Jinfu DUAN Xianzhong . Reac tive power optimization of distribution network with wind turbine
[J]. Proceedings of the CSEE , 2008 (7 ):40 -45 .
URL
[本文引用: 2]
研究了分布式电源中发展较为成熟的风力发电机组并网后配电网的无功优化问题,提出一种基于场景发生概率的无功优化综合指标,该指标由网损和静态电压稳定裕度两部分构成。基于该指标,提出一种新的无功优化模型。在该模型中,提出风电机组输出功率典型场景的选取策略,无功优化潮流计算中考虑了风电机组的特点,将其作为电压静特性节点处理。在求解方法上,采用基于自适应权重的遗传算法求解。算例表明,提出的模型和算法是可行的,对风电系统的运行具有一定的参考价值。
[8]
陈旭 , 杨雨瑶 , 张勇军 , 等 . 光伏光照概率性对配电网电压的影响
[J]. 华南理工大学学报 , 2015 (4 ):112 -118 .
[本文引用: 1]
CHEN Xu YANG Yuyao ZHANG Yongjun , et al . Influence of illumination probability of photovoltaic system on voltage of power distribution networks
[J]. Journal of South China University of Technology , 2015 (4 ):112 -118 .
[本文引用: 1]
[9]
王成山 , 郑海峰 , 谢莹华 , 等 . 计及分布式发电的配电系统随机潮流计算
[J]. 电力系统自动化 , 2005 ,29 (24 ):39 -44 .
[本文引用: 1]
WANG Chengshan ZHENG Haifeng XIE Yinghua , et al . Probabilistic power flow containing distributed generation in distribution system
[J]. Automation of Electric Power Systems , 2005 ,29 (24 ):39 -44 .
[本文引用: 1]
[10]
王淳 , 高元海 . 基于概率统计的含间歇性分布式发电的配电网无功优化
[J]. 电网技术 , 2014 (4 ):1032 -1037 .
DOI:10.13335/j.1000-3673.pst.2014.04.032
URL
[本文引用: 1]
以有功网损期望值最小为优化目标,以节点电压的合格概率大于一定的阈值为约束条件,建立了同时考虑风能、太阳能分布式发电出力和负荷随机波动的配电网无功优化模型。目标函数和约束项中所涉及的概率潮流由一种结合传统解析法的基于全概率公式的计算方法求得。使用化学反应算法对所建优化模型进行求解。在同时接入风能、太阳能分布式电源的33节点和69节点系统上对所提方法进行了验证,得到了具有概率统计意义的最优方案。通过与包括遗传算法(genetic algorithm,GA)、Stud GA(stud genetic algorithm)、生物地理学算法(biogeography based optimization,BBO) 和粒子群算法(particle swarm optimization,PSO)在内的多个智能算法对比,验证了所构建的化学反应算法在求解上述无功优化模型时性能更加稳定。
WANG Chun GAO Yuanhai . Probability statistics based reactive power optimization of distribution network containing intermittent distributed generations
[J]. Power System Technology , 2014 (4 ):1032 -1037 .
DOI:10.13335/j.1000-3673.pst.2014.04.032
URL
[本文引用: 1]
以有功网损期望值最小为优化目标,以节点电压的合格概率大于一定的阈值为约束条件,建立了同时考虑风能、太阳能分布式发电出力和负荷随机波动的配电网无功优化模型。目标函数和约束项中所涉及的概率潮流由一种结合传统解析法的基于全概率公式的计算方法求得。使用化学反应算法对所建优化模型进行求解。在同时接入风能、太阳能分布式电源的33节点和69节点系统上对所提方法进行了验证,得到了具有概率统计意义的最优方案。通过与包括遗传算法(genetic algorithm,GA)、Stud GA(stud genetic algorithm)、生物地理学算法(biogeography based optimization,BBO) 和粒子群算法(particle swarm optimization,PSO)在内的多个智能算法对比,验证了所构建的化学反应算法在求解上述无功优化模型时性能更加稳定。
[11]
汪文达 , 崔雪 , 马兴 , 等 . 考虑多个风电机组接入配电网的多目标无功优化
[J]. 电网技术 , 2015 ,39 (7 ):1860 -1865 .
DOI:10.13335/j.1000-3673.pst.2015.07.015
URL
[本文引用: 1]
针对多个风电机组接入配电网带来的不确定性问题,采用基于拉丁超立方采样的Monte Carlo概率潮流计算方法(correlation Latin hypercube sampling Monte Carlo simulation,CLMCS)以及场景缩减技术得到风机组输出功率的典型场景,将不确定性问题转化为单场景确定性潮流问题。并建立以有功网损最小、电压偏差最小作为目标函数的配电网无功优化数学模型。采用ε 正交多目标差分进化算法(ε -orthogonal differential evolution multi-objective algorithm, ε -ODEMO)进行计算得到非劣解集,该算法基于一般差分演化算法,结合正交实验方法使初始个体均匀分布在决策变量空间,利用ε占优技术对Archive群体进行更新,能得到均匀分布的非劣解集。应用IEEE 33节点以及PG&E 69节点配电网系统进行了测试,结果验证了所提方法和模型的可行性与有效性。
WANG Wenda CUI Xue MA Xing , et al . Multi-objective optimal reactive power flow of distribution network with multiple wind turbines
[J]. Power System Technology , 2015 ,39 (7 ):1860 -1865 .
DOI:10.13335/j.1000-3673.pst.2015.07.015
URL
[本文引用: 1]
针对多个风电机组接入配电网带来的不确定性问题,采用基于拉丁超立方采样的Monte Carlo概率潮流计算方法(correlation Latin hypercube sampling Monte Carlo simulation,CLMCS)以及场景缩减技术得到风机组输出功率的典型场景,将不确定性问题转化为单场景确定性潮流问题。并建立以有功网损最小、电压偏差最小作为目标函数的配电网无功优化数学模型。采用ε 正交多目标差分进化算法(ε -orthogonal differential evolution multi-objective algorithm, ε -ODEMO)进行计算得到非劣解集,该算法基于一般差分演化算法,结合正交实验方法使初始个体均匀分布在决策变量空间,利用ε占优技术对Archive群体进行更新,能得到均匀分布的非劣解集。应用IEEE 33节点以及PG&E 69节点配电网系统进行了测试,结果验证了所提方法和模型的可行性与有效性。
[12]
RABIEE A SOROUDI A MOHAMMADI-IVATLOO B , et al . Corrective voltage control scheme considering demand response and stochastic wind power
[J]. IEEE Transactions on Power Systems , 2014 ,29 (6 ):2965 -2973 .
DOI:10.1109/TPWRS.2014.2316018
URL
[本文引用: 1]
This paper proposes a new approach for corrective voltage control (CVC) of power systems in presence of uncertain wind power generation and demand values. The CVC framework deals with the condition that a power system encounters voltage instability as a result of severe contingencies. The uncertainty of wind power generation and demand values is handled using a scenario-based modeling approach. One of the features of the proposed methodology is to consider participation of demand-side resources as an effective control facility that reduces control costs. Active and reactive redispatch of generating units and involuntary load curtailment are employed along with the voluntary demand-side participation (demand response) as control facilities in the proposed CVC approach. The CVC is formulated as a multi-objective optimization problem. The objectives are ensuring a desired loading margin while minimizing the corresponding control cost. This problem is solved using-constraint method, and fuzzy satisfying approach is employed to select the best solution from the Pareto optimal set. The proposed control framework is implemented on the IEEE 118-bus system to demonstrate its applicability and effectiveness.
[13]
文天舒 , 马平 , 董跃哲 . 含多种分布式电源的配电网概率无功优化
[J]. 云南民族大学学报 , 2019 ,28 (4 ):382 -388 .
[本文引用: 1]
WEN Tianshu MA Ping DONG Yuezhe . Probabilistic reactive power optimization of distribution network with multi-distributed generation types
[J]. Journal of Yunnan University of Nationalities , 2019 ,28 (4 ):382 -388 .
[本文引用: 1]
[14]
黄升 . 分布式电源对配电网的影响及优化配置模型
[J]. 大电机技术 , 2016 (6 ):62 -64 .
[本文引用: 1]
HUANG Sheng . Effect of distributed generation on distribution and optimal allocation model
[J]. Large Motor Technology , 2016 (6 ):62 -64 .
[本文引用: 1]
[15]
张敬安 , 王雷涛 , 王鹏 . 交直流混合配电网电能质量综合检测和补偿方法
[J]. 电气工程学报 , 2018 ,13 (9 ):38 -43 .
[本文引用: 1]
ZHANG Jingan WANG Leitao WANG Peng . Power quality detection and compensation method of AC/DC hybrid distribution network
[J]. Journal of Electrical Engineering , 2018 ,13 (9 ):38 -43 .
[本文引用: 1]
[16]
王晓龙 . 基于两点估计法的电力系统概率潮流计算
[D]. 太原:太原理工大学 , 2013 .
[本文引用: 2]
WANG Xiaolong . Probabilistic power flow calculation of power system based on two-point estimation method
[D]. Taiyuan:Taiyuan University of Technology , 2013 .
[本文引用: 2]
[17]
MOHSENI-BONAB S M RABIEE A MOHAMMADI- IVATLOO B , et al . A two-point estimate method for uncertainty modeling in multi-objective optimal reactive power dispatch problem
[J]. International Journal of Electrical Power & Energy Systems , 2016 ,75 :194 -204 .
DOI:10.1016/j.ijepes.2015.08.009
URL
[本文引用: 1]
[18]
潘曙冰 , 陆政 , 高莹 , 等 . 计及分布式电源功率不确定性的配电网多目标无功优化
[J]. 电气自动化 , 2018 ,40 (1 ):70 -73 .
[本文引用: 1]
PAN Shubing LU Zheng GAO Ying , et al . Multi-objective reactive power optimization of the distribution network considering DG power uncertainties
[J]. Electrical Automation , 2018 ,40 (1 ):70 -73 .
[本文引用: 1]
[19]
徐雄风 . 含分布式电源的配电网无功优化研究
[D]. 淮南:安徽理工大学 , 2018 .
[本文引用: 1]
XU Xiongfeng . Research on reactive power optimization of distribution network with distributed generation
[D]. Anhui:Anhui University of Science and Technology , 2018 .
[本文引用: 1]
[20]
周林波 , 石平灯 , 田滔 , 等 . 粒子群算法在电网无功优化中的应用研究
[J]. 电力大数据 , 2019 ,22 (9 ):79 -85 .
[本文引用: 1]
ZHOU Linbo SHI Pingdeng TIAN Tao , et al . Application of particle swarm optimization on grid reactive power optimization
[J]. Power Systems and Big Data , 2019 ,22 (9 ):79 -85 .
[本文引用: 1]
[21]
王守相 , 王成山 . 现代配电系统分析 [M]. 2版. 北京 : 高等教育出版社 , 2014 .
[本文引用: 1]
WANG Shouxiang WANG Chengshan . Modern power distribution system analysis [M]. 2nd ed. Beijing : Higher Education Press , 2014 .
[本文引用: 1]
新能源配电网低碳高效运行的可拓层次评估方法
1
2018
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
新能源配电网低碳高效运行的可拓层次评估方法
1
2018
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
含分布式电源的配电网无功优化研究综述
1
2017
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
含分布式电源的配电网无功优化研究综述
1
2017
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
新一代电力系统灵活柔性特征研究
1
2019
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
新一代电力系统灵活柔性特征研究
1
2019
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
基于改进粒子群算法的含DG配电网无功优化
1
2018
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
基于改进粒子群算法的含DG配电网无功优化
1
2018
... 随着世界能源危机和环境问题的日益严重,可再生能源发电以其绿色环保、资源丰富的优点在电力行业中所占的比例越来越高,其中分布式电源并网发电的影响最大[1 ] .但分布式电源具有很强的出力随机性,接入电网后会改变原系统的潮流分布,以及对系统的网络损耗和节点电压产生不利影响,甚至会影响系统的安全与稳定,使得配电网无功优化问题变的更加复杂[2 ] .含DG的配电网无功优化是指DG接入电网后,在满足系统各项运行约束条件下,通过对系统中的控制变量进行优化配置,以减小系统损耗,提高电压质量[3 ] .所以,含DG的配电网无功优化是一个复杂的、非线性的优化问题[4 ] . ...
包含分布式电源的配电网无功优化
1
2011
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
包含分布式电源的配电网无功优化
1
2011
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
含多个风电机组的配电网无功优化
2
2010
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
... ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
含多个风电机组的配电网无功优化
2
2010
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
... ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
含风电机组的配网无功优化
2
2008
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
... ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
含风电机组的配网无功优化
2
2008
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
... ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
光伏光照概率性对配电网电压的影响
1
2015
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
光伏光照概率性对配电网电压的影响
1
2015
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
计及分布式发电的配电系统随机潮流计算
1
2005
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
计及分布式发电的配电系统随机潮流计算
1
2005
... 针对含DG的配电网无功优化问题,学者们进行了大量的研究,文献[5 ]将分布式电源出力的随机性进行了恒定化处理,以系统有功网损最小为目标进行配电网的无功优化,其优化结果对分布式电源的强出力随机性只具有一定的参考意义.文献[6 ]利用场景分析法将风机出力分为三种运行场景,分别为额定、停机和前额定运行,并且每一种运行场景的风机出力为其对应风速区间的平均值.文献[7 ]对配电系统中同时接入多个参数不同的风电机组的情况,采用多场景划分得方法来对配网进行无功优化.文献[6 ,7 ]对含风机的配网无功优化所用的方法对场景的选择较为困难,以及对场景概率的计算过于复杂,并且对风电出力值的确定不准确,难以反映出风机出力的随机性,而场景划分得过多又会使风电出力在短时间内场景的改变过于频繁,造成控制设备不必要的损坏.文献[8 ]通过模拟光伏发电系统在三种典型天气情况下的出力变动,讨论了光伏发电对电网稳定性的影响,但对配电网无功优化中的随机性因素考虑不全面,分布式电源的选择较为单一,只考虑了光伏发电对配电网的影响,未涉及到风力发电的影响.文献[9 ]全面考虑了负荷的不定性以及分布式电源出力的波动性,创建了配电网的无功优化模型,采用半不变量法对模型中的随机潮流问题进行求解,该方法相对全面地考虑了无功优化模型中的不定因素,但其所选的模型求解方法使计算过程过于复杂. ...
基于概率统计的含间歇性分布式发电的配电网无功优化
1
2014
... 风速$v$是根据天气情况而不断变化的,历史研究数据表明,威布尔(Weibull)分布[10 ,11 ] 对风速进行的统计描述较为准确,则风速的概率密度函数为 ...
基于概率统计的含间歇性分布式发电的配电网无功优化
1
2014
... 风速$v$是根据天气情况而不断变化的,历史研究数据表明,威布尔(Weibull)分布[10 ,11 ] 对风速进行的统计描述较为准确,则风速的概率密度函数为 ...
考虑多个风电机组接入配电网的多目标无功优化
1
2015
... 风速$v$是根据天气情况而不断变化的,历史研究数据表明,威布尔(Weibull)分布[10 ,11 ] 对风速进行的统计描述较为准确,则风速的概率密度函数为 ...
考虑多个风电机组接入配电网的多目标无功优化
1
2015
... 风速$v$是根据天气情况而不断变化的,历史研究数据表明,威布尔(Weibull)分布[10 ,11 ] 对风速进行的统计描述较为准确,则风速的概率密度函数为 ...
Corrective voltage control scheme considering demand response and stochastic wind power
1
2014
... 一般认为太阳光照强度$r$近似服从 Beta 分布[12 ,13 ] ,即 ...
含多种分布式电源的配电网概率无功优化
1
2019
... 一般认为太阳光照强度$r$近似服从 Beta 分布[12 ,13 ] ,即 ...
含多种分布式电源的配电网概率无功优化
1
2019
... 一般认为太阳光照强度$r$近似服从 Beta 分布[12 ,13 ] ,即 ...
分布式电源对配电网的影响及优化配置模型
1
2016
... 一般认为基于预测的负荷功率具有正态分布[14 ,15 ] ,则负荷功率的概率密度函数可表示为 ...
分布式电源对配电网的影响及优化配置模型
1
2016
... 一般认为基于预测的负荷功率具有正态分布[14 ,15 ] ,则负荷功率的概率密度函数可表示为 ...
交直流混合配电网电能质量综合检测和补偿方法
1
2018
... 一般认为基于预测的负荷功率具有正态分布[14 ,15 ] ,则负荷功率的概率密度函数可表示为 ...
交直流混合配电网电能质量综合检测和补偿方法
1
2018
... 一般认为基于预测的负荷功率具有正态分布[14 ,15 ] ,则负荷功率的概率密度函数可表示为 ...
基于两点估计法的电力系统概率潮流计算
2
2013
... 两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值.由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算. ...
... 通过使用均值$aver\_{{x}_{i}}$两侧的两个变量${{x}_{i1}}$和${{x}_{i2}}$来匹配随机量${{x}_{i}}$的前三阶矩,以取代该节点注入量的概率密度函数,计算过程详见文献[16 ].则对某一节点随机变量${{x}_{i}}$用2×n 组数据进行确定性潮流计算 ...
基于两点估计法的电力系统概率潮流计算
2
2013
... 两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值.由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算. ...
... 通过使用均值$aver\_{{x}_{i}}$两侧的两个变量${{x}_{i1}}$和${{x}_{i2}}$来匹配随机量${{x}_{i}}$的前三阶矩,以取代该节点注入量的概率密度函数,计算过程详见文献[16 ].则对某一节点随机变量${{x}_{i}}$用2×n 组数据进行确定性潮流计算 ...
A two-point estimate method for uncertainty modeling in multi-objective optimal reactive power dispatch problem
1
2016
... 两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值.由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算. ...
计及分布式电源功率不确定性的配电网多目标无功优化
1
2018
... 两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值.由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算. ...
计及分布式电源功率不确定性的配电网多目标无功优化
1
2018
... 两点估计法是求解概率潮流的一种近似方法[16 ,17 ,18 ] ,在每个不确定变量的均值两侧确定两个值,并用这两个值来代替该随机变量,同时其他不确定变量均取为均值.由此可知,若系统中有n 个随机变量,那就需要进行2n 次的确定性潮流计算. ...
含分布式电源的配电网无功优化研究
1
2018
... 粒子群算法以其简单、易实现等突出特点在离散型数学模型的求解中应用最为广泛[19 ,20 ] .可是在标准粒子群算法的使用中,惯性权重和学习因子通常被取为常数,在参数恒定的情况下,算法在后期迭代寻优过程中易陷入局部最优,造成早熟的现象.所以,为保持迭代过程中粒子的多样性,需要对参数进行改进从而克服算法出现局部最优解的缺陷,使算法在迭代前期具有较强的全局搜索能力,提高种群多样性,而在后期具有更强的局部搜索能力,提高寻优精度和速度. ...
含分布式电源的配电网无功优化研究
1
2018
... 粒子群算法以其简单、易实现等突出特点在离散型数学模型的求解中应用最为广泛[19 ,20 ] .可是在标准粒子群算法的使用中,惯性权重和学习因子通常被取为常数,在参数恒定的情况下,算法在后期迭代寻优过程中易陷入局部最优,造成早熟的现象.所以,为保持迭代过程中粒子的多样性,需要对参数进行改进从而克服算法出现局部最优解的缺陷,使算法在迭代前期具有较强的全局搜索能力,提高种群多样性,而在后期具有更强的局部搜索能力,提高寻优精度和速度. ...
粒子群算法在电网无功优化中的应用研究
1
2019
... 粒子群算法以其简单、易实现等突出特点在离散型数学模型的求解中应用最为广泛[19 ,20 ] .可是在标准粒子群算法的使用中,惯性权重和学习因子通常被取为常数,在参数恒定的情况下,算法在后期迭代寻优过程中易陷入局部最优,造成早熟的现象.所以,为保持迭代过程中粒子的多样性,需要对参数进行改进从而克服算法出现局部最优解的缺陷,使算法在迭代前期具有较强的全局搜索能力,提高种群多样性,而在后期具有更强的局部搜索能力,提高寻优精度和速度. ...
粒子群算法在电网无功优化中的应用研究
1
2019
... 粒子群算法以其简单、易实现等突出特点在离散型数学模型的求解中应用最为广泛[19 ,20 ] .可是在标准粒子群算法的使用中,惯性权重和学习因子通常被取为常数,在参数恒定的情况下,算法在后期迭代寻优过程中易陷入局部最优,造成早熟的现象.所以,为保持迭代过程中粒子的多样性,需要对参数进行改进从而克服算法出现局部最优解的缺陷,使算法在迭代前期具有较强的全局搜索能力,提高种群多样性,而在后期具有更强的局部搜索能力,提高寻优精度和速度. ...
1
2014
... 本文采用改进的IEEE33节点配电系统进行仿真测试,并通过Matlab软件进行编程实现.系统的原始数据详见文献[21 ]. ...
1
2014
... 本文采用改进的IEEE33节点配电系统进行仿真测试,并通过Matlab软件进行编程实现.系统的原始数据详见文献[21 ]. ...