基于磁场传感与北斗定位的采空区输电杆塔倾斜预警方法*

doi:10.11985/2020.03.006

基于磁场传感与北斗定位的采空区输电杆塔倾斜预警方法^*

宰红斌^,¹, 韩海安^,², 上官明霞², 单荣荣^,³

1.国网晋城供电公司运维检修部晋城 048000

2.国网山西省电力公司科技部太原 030021

3.国电南瑞科技股份有限公司南京 211106

Early Warning Method of Transmission Tower Inclination in Goaf Based on Magnetic Field Sensing and Beidou Positioning

ZAI Hongbin^,¹, HAN Haian^,², SHANGGUAN Mingxia², SHAN Rongrong^,³

1. Operation and Maintenance Department, State Grid Jincheng Power Supply Company, Jincheng 048000

2. Department of Science and Technology, State Grid Shanxi Electric Power Company, Taiyuan 030021

3. NARI Technology Development Co., Ltd., Nanjing 211106

收稿日期: 2020-04-30 修回日期: 2020-07-17 网络出版日期: 2020-09-25

基金资助:

* 国家重点研发计划(面向新型城镇的能源互联网关键技术及应用). 2018YFB0905000

Received: 2020-04-30 Revised: 2020-07-17 Online: 2020-09-25

作者简介 About authors

宰红斌,男,1971年生,高级工程师。主要研究方向为输电线路防灾减灾,运行维护与带电作业等。E-mail：qazw3182@163.com

韩海安,男,1969年生,硕士,高级工程师。主要研究方向为工业工程。E-mail：153336669269@163.com

sgmx58787963@126.com

单荣荣,男,1986年生,硕士,工程师。主要研究方向为电力物联网、电力系统自动化。E-mail：srr877374@163.com

摘要

现有采空区输电杆塔倾斜监测预警方法存在监测实时性弱、准确度低、受单一参数影响的缺陷。针对这一问题,提出一种基于磁场传感与北斗定位的采空区输电杆塔倾斜监测与预警方法。首先,建立采空区输电杆塔的磁场传感模型,计算输电线磁通密度。然后,结合北斗卫星定位技术,基于双因素分级叠合的方法,在监测杆塔运行状态的同时判断杆塔倾斜危险性程度等级。最后,通过三种故障情况下的算例结果表明,与传统的依靠单一手段进行输电杆塔状态监测预警的方法相比,所提方法的预测准确度平均提升了8.66%以上,故障反应速度平均提升了38.01%以上,从而验证了所提方法的有效性与优异性。

关键词： 采空区 ; 输电杆塔 ; 磁场传感 ; 北斗定位 ; 倾斜监测 ; 故障预警

Abstract

The existing monitoring and early-warning methods of transmission tower tilting in goafs have the shortcomings of weak real-time monitoring, low accuracy, and affected by a single parameter. Aiming at this problem, a tilt monitoring and early warning method for transmission towers in mined-out areas based on magnetic field sensing and Beidou positioning is proposed. First, a magnetic field sensing model of a transmission tower in a goaf is established, and the magnetic flux density of the transmission line is calculated. Then, combined with Beidou satellite positioning technology, based on the two-factor hierarchical superposition method, the tower’s tilting danger level is determined while monitoring the operating status of the tower. Finally, the calculation results of the three kinds of fault situations show that compared with the traditional method of relying on a single method for the monitoring and early warning of transmission tower conditions, the accuracy of the proposed method has increased by an average of 8.66% or more, and the reaction speed of faults has increased on average. It is more than 38.01%, which verifies the effectiveness and superiority of the proposed method.

Keywords： Goaf ; transmission tower ; magnetic field sensing ; Beidou positioning ; tilt monitoring ; failure warning

PDF (538KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

宰红斌, 韩海安, 上官明霞, 单荣荣. 基于磁场传感与北斗定位的采空区输电杆塔倾斜预警方法^*. 电气工程学报[J], 2020, 15(3): 44-49 doi:10.11985/2020.03.006

ZAI Hongbin, HAN Haian, SHANGGUAN Mingxia, SHAN Rongrong. Early Warning Method of Transmission Tower Inclination in Goaf Based on Magnetic Field Sensing and Beidou Positioning. Journal of Electrical Engineering[J], 2020, 15(3): 44-49 doi:10.11985/2020.03.006

1 引言

随着电网向特高压大电网不断发展,输电线路的安全运行涉及多项经济、技术指标。其中,采空区因地质倾斜与沉降产生的非荷载应力将极有可能导致杆塔构件破坏、断裂、变形,造成电气安全距离不够、故障跳闸、倒杆塔断线等严重事故的发生^[1,2]。

为了保证输电线路的安全稳定运行,已有研究提出多种针对防雷绝缘^[3]、形变倾斜^[4]、风偏闪络^[5]等的监测防治方案。如文献[6]研究了基于地面散射电流的分散式监测技术,但这一方案主要保障了在线监测的有效可靠,对离线监测没有突出的改进;文献[7]通过特征聚类实现了输电线路绝缘子的红外定位及自动辨识,但这一方案过度依赖先验参数的选取且不具有普遍适用性;文献[8]建立了四跨绝缘子串-导线耦合体系有限元模型以确定输电线路的风偏闪络,但拟合公式的方法计算结果较正常值小,而刚性直棒法没有考虑风速的脉动影响。

采空区的地表会发生塌陷或水平移动的地质形态改变,这一地质变化更易造成输电杆塔的倾斜与基础不均匀沉降,导致输电杆塔发生严重的电气事故。针对这一区域的输电杆塔监测,文献[9]提出基于扩频编码的电磁探测系统,实现采空区的有效勘探,虽然提高了探测效率,但电磁探测系统准确度的提高以强发射功率为代价,经济性差;文献[10]基于北斗卫星实现输电杆塔的在线监测,但这一方案不能满足离线状态下的数据分析要求;文献[11]通过采空区输电杆塔的承载力计算,判断倾斜位移的安全范围,这一方案虽然为安全运行提供参考依据,但不能对杆塔状态进行在线监测。

上述针对采空区输电杆塔的监测方法,均难以同时满足监测系统的经济性和实时性要求。因此提出基于磁场传感与北斗定位的采空区输电杆塔倾斜监测与预警方法,通过磁阻传感器与北斗定位等多源监测信息融合,基于双因素分级叠合法,有效构建输电杆塔的风险预警,提高了故障检测的响应速度与运维能力;通过TMR传感器得到磁通值波动情况,以及其与对应杆塔倾斜监测预警影响因子之间的关系,实现对故障程度的有效判断及预警。

2 磁场传感模型

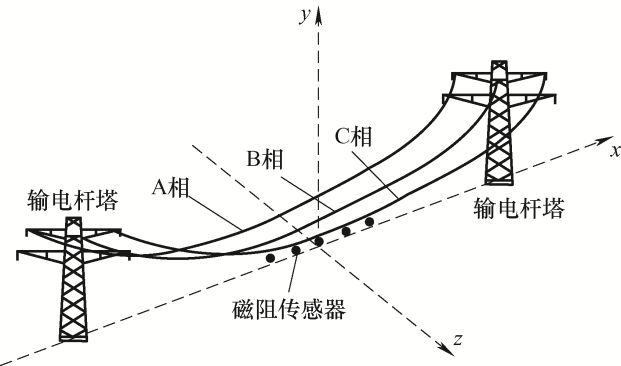
通过磁场传感的杆塔监测模式,首先需要确定架空输电线的磁场方程,如图1所示是典型的输电塔之间的高压传输线示意图,A、B、C三相输电线周围的磁场分布受悬链线形状及其相对位置的影响。测试模型简化为三相传输线的下垂程度相同,通过叠加原理即可计算三相传输线产生的磁通密度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 输电线路示意图

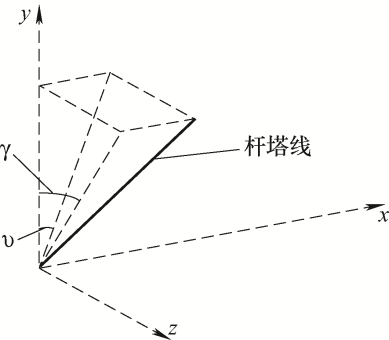
如图2所示是输电线路的笛卡儿坐标系简化图,假设左侧杆塔倾斜,则可以确定y轴与塔筒在x-y平面上的投影之间的角度υ、y轴与塔筒在z-y平面上的投影之间的角度γ,通过υ和γ即可确定塔的倾斜程度。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 输电杆塔倾斜程度示意图

使用抛物线近似来描述传输线曲线,悬链线方程的近似值如文献[12,13]所述,传输线B在x-y平面中,并且相对于y轴对称分布

(1)$\left\{ \begin{align} & y=\upsilon {{x}^{2}}+l \\ & \upsilon =\frac{4u}{{{H}^{2}}} \\ \end{align} \right.$

式中,u为传输线垂度;l为距地面最低点的高度;H为两座相邻塔的距离。应用Biot-Savart定律计算磁通密度,中距传输线B的空间中的点B₀(x₀,y₀,z₀)的磁场方程为

(2)$\left\{ \begin{matrix} {{B}_{0}}=\frac{{{\zeta }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}\sum\limits_{i=1}^{M}{\sum\limits_{k=-N}^{N}{\int\limits_{-H/2}^{H/2}{({{W}_{x}}{{e}_{x}}+{{W}_{y}}{{e}_{y}}+{{W}_{z}}{{e}_{z}})}}}\text{d}x \\ {{W}_{x}}=\frac{{{i}_{bi}}2\upsilon {{z}_{0}}x}{4\text{ }\!\!\pi\!\!\text{ }{{b}_{i}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ {{W}_{y}}=-\frac{{{i}_{bi}}{{z}_{0}}}{4\text{ }\!\!\pi\!\!\text{ }{{b}_{i}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ {{W}_{z}}=\frac{{{i}_{bi}}(\upsilon {{x}^{2}}+{{y}_{0}}-l)}{4\text{ }\!\!\pi\!\!\text{ }{{b}_{i}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ {{b}_{i}}={{[{{(x-{{x}_{0}})}^{2}}+z_{0}^{2}+{{({{y}_{0}}-\upsilon {{x}^{2}}-l)}^{2}}]}^{3/2}}\ \ \ \ \ \ \\ \end{matrix} \right.$

式中,支撑结构上的单个导体的数量指定为M;ζ₀为自由空间的渗透性;i_bi为传输线B中的电流;e为源到场点的单位矢量。

但是,当塔架倾斜时,确定传输线和磁场方程就变得非常困难,因为在xyz坐标系中单个传输线的z值并不相同,另外即使可以解得方程组的解,方程式也非常复杂。因此,使用几何变换解决这一问题,点到点的几何变换映射不会增加方程式的复杂程度。因此,转换图2中的坐标系简化方程式,变换原始坐标系遵循以下两种原理。

(1) 保证传输线i在x_i-y_i-z_i坐标系中的x_i-y_i平面中(i=A、B、C)。

(2) 保证x-z平面和x_i-z_i平面在同一平面上(i=A、B、C)。

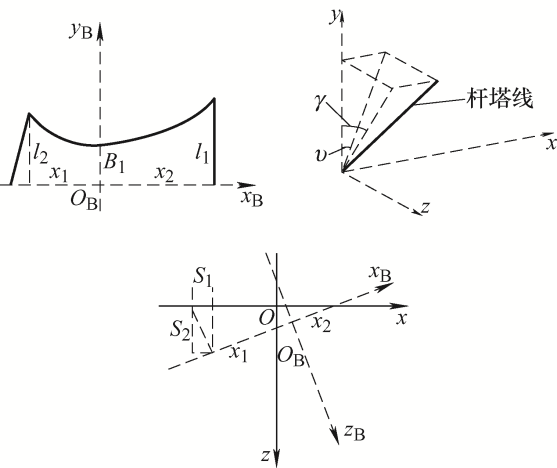
建立x_B-y_B-z_B坐标系,令B₁和B₂是传输线B的悬置点在倾斜之前在x-y平面上的投影,B′是倾斜后传输线B的悬浮点在x-y平面上的投影。得到倾斜后建立的新坐标系x_B-y_B-z_B,而y_B轴始终垂直于地面,令倾斜后传输线B最低点在x-z平面上的投影点为B_xz,l_B是倾斜后距地面最低点的高度,倾斜前悬挂点高度为l₁,倾斜后悬挂点高度为l₂。倾斜前后传输线B的形状方程发生了变化的同时,积分范围、距地面最低点的高度和传输线B在空间中的点B₀(x₀,y₀,z₀)的数值都发生了变化,如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 杆塔倾斜后的传输线在坐标系中的变化

根据图3中的几何关系,可以得到

(3)$\left\{ \begin{align} & {{S}_{1}}={{l}_{2}}\tan \upsilon \\ & {{S}_{\text{2}}}={{l}_{2}}\tan \gamma \\ & {{l}_{1}}=\sqrt{{{l}_{2}}^{2}+{{S}_{1}}^{2}+{{S}_{2}}^{2}} \\ \end{align} \right.$

由于相对于最低点的线的形状不受塔倾角的影响,因此抛物线形状仍可以用来表示x_B-y_B-z_B坐标系中的传输线B,为

(4)${{y}_{\text{B}}}^{2}={{({{\upsilon }_{\text{B}}}{{x}_{\text{B}}}^{2}\text{)}}^{\text{2}}}\text{+}{{B}_{l}}^{2}$

其中,x₁、x₂、B_l和υ_B表示为

(5)$\left\{ \begin{align} & \upsilon {}_{\text{B}}{{x}_{1}}^{2}+{{B}_{l}}={{l}_{1}} \\ & {{\upsilon }_{\text{B}}}x{{{}_{2}}^{2}}+{{B}_{l}}={{l}_{2}} \\ & {{x}_{1}}+{{x}_{2}}=\sqrt{{{(H-{{S}_{1}})}^{2}}+{{S}_{2}}^{2}} \\ \end{align} \right.$

其中积分环节如式(2)所示。可以得到,在塔倾斜前后,传输线B的长度保持相同。

倾斜后的原点O_B通过三角形变换求得

(6)$\frac{{{x}_{2}}}{{{x}_{1}}+{{x}_{2}}}=\frac{H/2-{{x}_{{{O}_{\text{B}}}}}-{{y}_{{{O}_{\text{B}}}}}}{H-{{S}_{1}}}=\frac{{{z}_{{{O}_{\text{B}}}}}}{{{S}_{2}}}$

式中,(${{x}_{{{O}_{\text{B}}}}}$,${{y}_{{{O}_{\text{B}}}}}$,${{z}_{{{O}_{\text{B}}}}}$)为xy在xyz坐标系中的坐标。由于x-z平面和x_B-z_B平面在同一平面上,因此${{y}_{{{O}_{\text{B}}}}}$ 为零。

一旦获得x轴和变换后x_B轴的夹角α以及原点O_B的坐标,就可以相应地建立x_B-y_B-z_B坐标系,然后计算xyz坐标系中任意点(x,y,z)的x_B-y_B-z_B坐标系中的坐标(x_B,y_B,z_B),其中

y_B=y

(7)${{x}_{\text{B}}}=\sqrt{{{(x-{{x}_{{{O}_{\text{B}}}}})}^{2}}+{{(z-{{z}_{{{O}_{\text{B}}}}})}^{2}}}\cos \beta$

(8)${{z}_{\text{B}}}=\sqrt{{{(x-{{x}_{{{O}_{\text{B}}}}})}^{2}}+{{(z-{{z}_{{{O}_{\text{B}}}}})}^{2}}}\sin \beta$

(9)$\tan \beta =\frac{z-{{z}_{{{O}_{\text{B}}}}}}{x-{{x}_{{{O}_{\text{B}}}}}}+{{\alpha }_{\text{B}}}$

因此,在x_B-y_B-z_B坐标系中,点(x,y,z)可以用(${{x}_{{{O}_{\text{B}}}}}$,${{y}_{{{O}_{\text{B}}}}}$,${{z}_{{{O}_{\text{B}}}}}$)和α表示,则可以利用已知参数,确定x_B-y_B-z_B坐标系中点的磁通密度。在xyz坐标系中,传输线A和C产生的磁通密度的计算方法与传输线B相同,传输线A、B和C产生的总磁通密度为各项的分量加和。

3 结合北斗定位的倾斜监测与预警方法

提出的采空区输电系统监测预警方法,基于磁阻传感器与北斗定位等多源监测信息,对输电杆塔的倾斜变化进行监测,使用双因素分级叠合的方法,量化杆塔电流和杆塔位置变化程度,实现采空区的输电杆塔倾斜监测与预警。

如图1所示,杆塔之间设置有五个间隔为5 m的双轴磁阻传感器,传感器位于传输线B的最低点正下方。通过沿x轴五个磁阻传感器处磁通密度的yz分量B_y,B_z,能够估计出传输线的垂度和塔架倾斜角,通过估计参数可以精确地重建三相电流。由于y轴与塔筒在x-y平面上的投影之间的角度υ、y轴与塔筒在z-y平面上的投影之间的角度γ和垂度都影响了磁通密度的yz分量,因此测量B_y,B_z即可估算υ、γ和传输线垂度。

磁阻传感器可以测量地面传输线下的磁通密度,进而得到磁场分布,这里使用具有低成本、低功耗和高检测精度的隧道磁阻(Tunneling magnetoresistive,TMR)^[14],测得的磁场通过人工免疫系统算法的优化方法迭代更新,即可得到υ、γ和传输线垂度。首先根据υ、γ和传输线垂度求出预存储位置系数矩阵A,然后通过最小二乘估计法计算三相电流,推导出磁通密度,最后将计算出的和测得的磁场数据之间的绝对误差与精度阈值相比较,通过AIS算法更新预存储位置系数矩阵A,直到计算数据的和测得的磁场数据之间的绝对误差小于精度阈值,即得到准确的监测磁通值,监测磁通值的波动情况和其对应杆塔倾斜监测预警的影响因子G_I如表1所示。

表1 磁通波动及对应影响因子

监测磁通波动(%)	±0.05	±0.1	±0.25	±0.5
影响因子指数G_I	1	2	3	4

新窗口打开| 下载CSV

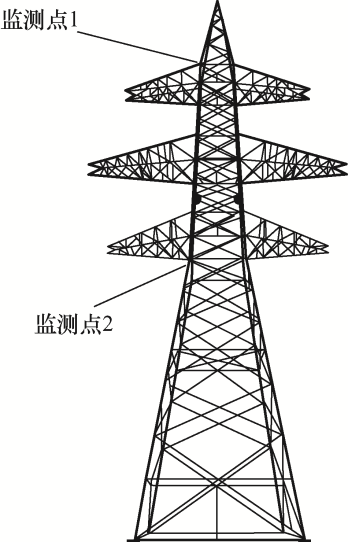
输电杆塔的北斗定位监测点如图4所示,选取杆塔附近30 km范围的稳定基岩,作为毫米级监测要求的基准站^[15,16],并埋设相对塔基位置固定且稳定的观测墩,以确保基准点的坐标固定不变。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 输电杆塔的北斗定位监测点示意图

倾斜程度可分为塔基座位置不变和塔基座位置变动两种情况,输电杆塔由t₀时刻的位置(x₀,y₀,z₀)倾斜至t时刻的位置(x',y',z' ),其中t=t₀+Δt。DLT/741—2019《架空输电线路运行规程》中规定杆塔变形的倾斜限值,将危险程度分为三个等级,塔基座位置不变时α ≤0.5%正常,0.5%≤α ≤1%预警,α ≥1%危险;塔基座位置变动时α ≤0.4%正常,0.4%≤α ≤0.8%预警,α ≥0.8%危险。

为准确刻画输电杆塔位置状态,将其倾斜度用状态因子G_S表示正常、预警和危险三个不同等级,如表2所示。

表2 杆塔危险程度及状态因子

杆塔状态	危险程度
杆塔状态	正常	预警	危险
塔基座位置不变	α≤0.5% G_S=1	0.5%≤α≤1% G_S=2	α≥1% G_S=3
塔基座位置变动	α≤0.4% G_S=1.5	0.4%≤α≤0.8% G_S=2.5	α≥0.8% G_S=4

新窗口打开| 下载CSV

使用双因素分级叠合的方法对杆塔电流和杆塔位置变化程度量化,即杆塔危险指数

$G={{G}_{I}}\centerdot {{G}_{S}}$

则存在输电杆塔倾斜预警等级如表3所示。

表3 输电杆塔倾斜预警等级

杆塔危险指数G	故障严重程度预警百分比(%)
1~4	0~25
5~8	26~50
9~12	51~75
13~16	76~100

新窗口打开| 下载CSV

综上所述,根据采空区输电杆塔的运行测试模型,使用倾斜度用状态因子G_S和磁通波动影响因子G_I描述输电杆塔的运行情况,通过双因素分级叠合计算杆塔危险指数,划分输电杆塔故障预警等级,实现依赖于磁场传感和北斗定位的倾斜监测预警。

4 试验结果与分析

使用四种不同情况下的采空区输电杆塔的模型对提出的方法进行试验验证,传输杆塔的正常运行状态为：传输线垂度u=10 m,y轴与塔筒在x-y平面上的投影之间的角度υ=0°,y轴与塔筒在z-y平面上的投影之间的角度γ=0°,输电线距地面最低点的高度l=10 m,两座相邻塔的距离H=100 m,A、B、C三相间距离b=10 m,频率为50 Hz,每相电流为1 kA。四种故障情况如表4所示。

表4 故障情况

故障情况	故障部位	故障原因
1	输电线	输电线距地面最低点的高度下垂至l=8 m
2	A相电流	A相发生-4°相移
3	B相电流	B相磁通波动增加至0.4％

新窗口打开| 下载CSV

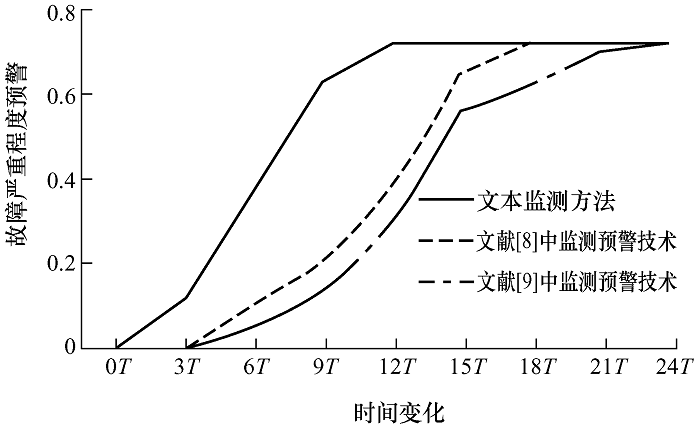
对比文献[8]中基于扩频编码的电磁探测技术和文献[9]中基于北斗卫星的在线监测方法,研究四种故障情况下的监测实时性和准确性。如图5所示是发生故障情况1时,25 T内监测实时性随时间变化的情况,T表示单位时间长度,输电线从2 T开始下垂,至10 T下垂至l=8 m。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 故障1情况下的监测方法实时性对比

由图5可知,在2~10 T发生传输线下垂的过程中,提出的监测方法相比文献[8,9]中方法具有更快的反应速度,在12 T时间内准确计算输电杆塔的故障严重程度,相比另外两种方法,响应速度分别提高33.33%和42.86%。

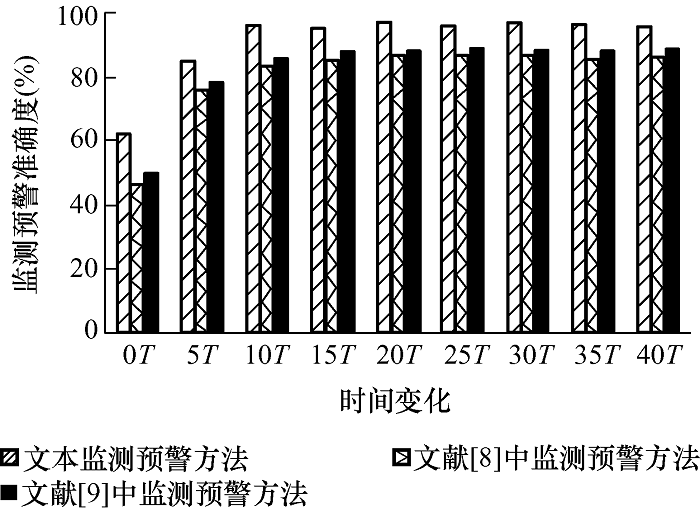
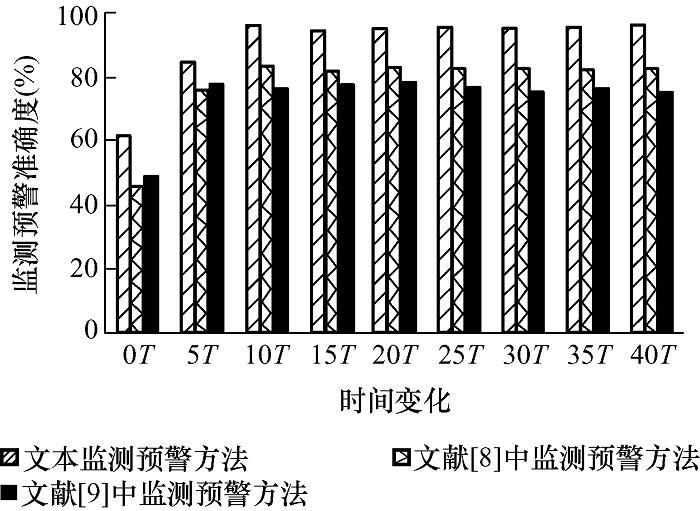
图6、7分别为故障情况2、故障情况3发生时,所提方法与文献[8]、[9]中提出方法的准确性对比,令T=0时,发生故障。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 故障2情况下的监测方法准确性对比

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 故障3情况下的监测方法准确性对比

由图6、7可知,本文提出的监测预警方法在发生中等及中等偏下程度的杆塔倾斜故障时,具有最快的反应速度,确认故障发生后的平均准确率分别为96.19%和96.17%。对比文献[8]、[9]中提出的方法,本文监测方法对于故障情况2中中等偏下程度的杆塔倾斜故障的平均监测预警准确率分别提高10.79%和8.66%,对于故障情况3中中等程度的杆塔倾斜故障的平均监测预警准确率分别提高13.21%和19.57%。对比现有方法,本文提出的监测预警方法显著提高了故障程度的监测准确度。

5 结论

针对已有输电杆塔倾斜监测方法判断标准单一、实时性差的问题,提出了一种基于磁场传感与北斗定位的采空区输电杆塔倾斜监测与预警方法。综合磁场传感器的磁通密度测量结果和北斗卫星定位技术,对磁通密度和输电杆塔倾斜程度进行双因素分级叠合,判断杆塔故障的严重程度等级,并进行预警,得出如下结论。

(1) 提出的采空区输电杆塔倾斜监测与预警方法,有效提高了故障监测响应速度和故障程度的监测准确度,在工程中对杆塔故障程度判定具有重要意义。

(2) 传感器的便携式平台便于工程人员快速简便地对已有杆塔升级改造,保证了在杆塔构件破坏、断裂、变形后的快速预警,有效预防故障跳闸、倒杆塔断线等严重事故的发生,减少经济损失。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨肖辉, 张东, 李晓光, 等.

750 kV输电线路风偏跳闸原因分析及改造措施研究

[J]. 电气工程学报, 2017,12(1):40-46.