随着大规模新能源并网,配电网的安全、稳定、可靠运行日益重要^[1]。由于配电网输电范围较广,线路错综复杂,容易发生短路故障。当系统发生单相接地故障时,接地电流大,常常伴有电弧^[2],电弧主要以稳定性电弧和间隙性电弧为主出现,电弧反复重燃或稳定燃烧,容易发展成永久性故障。输电馈线穿山越岭,也常发生经土壤、树木等高阻抗接地以及大于大地电阻下的低阻抗接地^[3-4]。以上几种单相接地的故障信息常表现出间歇性、微弱性等特点,容易造成故障的误判、漏判等。因此,本文建立识别模型主要是对这四种复杂的单相接地故障类型进行识别,包括稳定性电弧、间歇性电弧、非线性高阻、线性低阻四种接地状态。

目前,在配电网发生接地故障识别研究中,文献[5]利用Hilbert-Huang transform(HHT)提取零序电压的故障特征量,用卷积神经网络(Convolutional neural networks,CNN)分类器对不同接地故障类型进行识别。文献[6]采用离散小波变换构造故障电压和电流的时频矩阵,基于粒子群算法和贝叶斯分类器对配电网高阻接地故障进行识别。文献[7]利用配电网母线电压、主变低压侧电流信息等构造时频矩阵,并对其进行奇异值分解得到故障特征奇异谱的分布参数,以多级支持向量机分类器进行故障分类。传统的识别方法主要是将人为设计的特征提取器和机器学习算法相结合来实现故障识别。但人工提取的故障特征一般不能够准确刻画被识别对象,其次,传统机器学习也容易出现过拟合,陷入局部收敛点等问题。深度学习作为机器学习的一个重要分支,在配电网故障选线^[8]、电压暂降源识别^[9]以及时间序列等领域已取得了重大进展,具有分类性能更佳、适应性更强等优点。因此,本文为了解决配电网单相接地故障识别的难题,保证配电网稳定运行以及下一步的运作,在深度学习理论下,建立具有自动提取故障特征的CNN来实现四种故障类型的识别。

CNN主要包括四种层：输入层、卷积层、池化层、输出层。输入层用$x\text{=}\left\{ {{x}_{\text{1}}},{{x}_{\text{2}}},\cdot \cdot \cdot ,{{x}_{n}} \right\}$表示。其中$x$表示一维矢量。卷积层的计算公式为

式中,${{W}^{i}}$为第$i$层卷积核大小;${{b}^{i}}$为第$i$层偏置矢量;$\sigma $为激活函数。

池化层通过对上层卷积运算结果进行下采样,即

全连接层是对池化层进行全连接到一个维度上,即

输出层采用softmax多分类器对上层结果进行输出,即计算公式为

在CNN的前向传播中,常用神经元的激活函数包括Sigmoid、Tanh、ReLU函数。池化主要包括平均池化和最大池化两种方式。对于降低模型过拟合风险,可采用正则化操作,即加入额外的惩罚参数以及在训练过程中限制连接权重等。对于多分类问题,代价函数多采用交叉熵的方法,并与softmax回归函数一起使用,softmax函数为

交叉熵函数为

式中,${{y}_{i}}$表示第$i$种出现的可能性大小;${{y}_{i\_}}$表示第$i$种期望输出。

CNN各个网络层的搭建以及各个层的具体参数设置如表1所示。表1中给出的参数是故障识别效果最优的CNN模型参数。

CNN的反向传播中主要是优化各个模型参数,调整权重,以加速减小Loss值。为了寻找最合适的优化器,本文对常见的四种优化器进行了比较,包括随机梯度下降算法(Stochastic gradient descent, SGD)、动量优化法(Momentum)以及自适应Adadelta、Adam算法。SGD算法从一批样本随机选取一个样本进行模型权重系数的调整,参数更新 如下

式中,${{W}_{n}}$表示更新的参数;$\alpha $表示学习率;$f({{W}_{n}})$表示随机一个样本的梯度。

Momentum算法在SGD基础上,加入了一个动量,具有加快训练速度、减少训练过程振荡等优点。参数更新如下

式中,$\beta $表示动量的大小;${{V}_{n}}$表示过去一段时间加速度的积累。

Adadelta算法不需要指定全局学习率。Adam算法与随机梯度下降算法有所不同,是采用变化的学习率方法。

式中,$\nu $代表衰减梯度;$r$表示衰减学习率;$\delta $通常为一个常数。

降维的方法主要有线性降维和非线性降维两种。目前有一种t-SNE方法^[10],降维、聚类效果较好。该方法是将欧式距离转化为条件概率来衡量维度空间数据点之间的相似性。

在高维空间中第$i$样本与第$j$样本距离计算公式为

式中,${{\sigma }_{i}}$为高斯标准差,在第$i$样本与其他样本构成总的条件概率分布为${{p}_{i}}=\{{{p}_{1/i}},{{p}_{2/i}},\cdot \cdot \cdot ,{{p}_{i/i}},\cdot \cdot \cdot ,{{p}_{j/i}}\}$。

假设高维空间i、$j$样本映射到嵌入空间对应为m、n样本,则在嵌入空间相似度

在第$m$样本与其他样本构成总的条件概率分布为${{q}_{m}}=\{{{q}_{1/m}},{{q}_{2/m}},\cdot \cdot \cdot ,{{q}_{m/m}},\cdot \cdot \cdot ,{{q}_{n/m}}\}$。这样t-SNE总的目标就是去优化${{p}_{i}}$与${{q}_{m}}$的距离达到最小值。

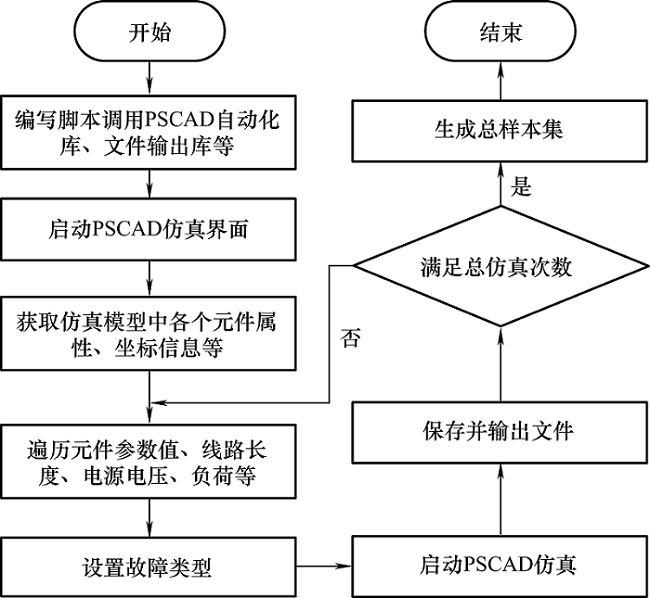
由于配电网各个采集装置性能存在差异,采样频率不同步,外界干扰大,很难形成一个统一、规范的单相接地故障样本集。因此本文采取自动、批量仿真的形式获取样本集。编写Python脚本程序,遍历修改配电网模型中的元件参数,并通过调用第三方自动化库与PSCAD进行交互,来形成整个自动化仿真流程,流程图如图1所示。选取在不同的过渡电阻、系统频率、故障位置、接地方式、故障初相角、系统电压以及负荷波动下进行仿真,参数值分布如表2所示。仿真结果总样本量为10 800个,其中每类故障样本量为2 700个,并对每类按照 8:1:1的比例随机分成训练集、验证集和测试集。训练集用于模型训练,验证集样本用于模型调整参数,测试集样本用于模型准确率测试。

初始特征采集位置和故障量的选择直接影响到模型的训练效果。文献[11]利用提取母线处三相电压、零序电压以及变压器低压侧母线电流,构造故障特征的时频能量矩阵,去识别配电网不同种接地故障类型。文献[12]提取三相电流、零序与负序电流以及零序有功功率、无功功率作为故障特征量,完成智能配电网故障识别。

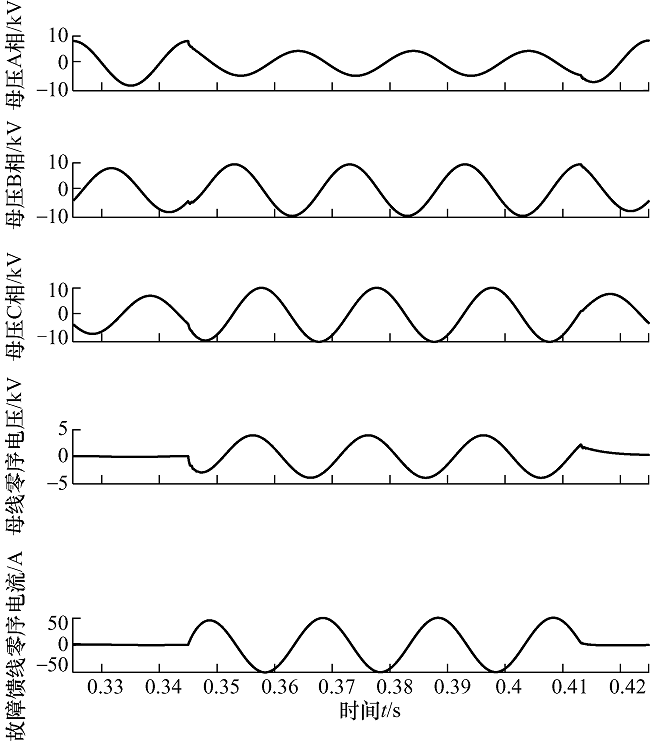
本文所研究的是辐射配电网接地故障识别,结合理论与大量试验分析,在一条支路发生单相接地故障时,提取主变压器低压侧母线处的三相电压、零序电压以及故障馈线零序电流共五个电气量作为样本训练数据。设置故障发生周期为三个周波,为了丰富样本信息,提取故障发生前、完成后各一周波的信息,即共采集故障信息五个周波,时间长度为0.1 s的数据。以低阻接地故障为例,单个样本数据如图2所示。波形采样率为$10\ \text{kHz}$,样本数据大小为1 000$\times $5。样本数据对应的标签采用一维数组表示,发生某类故障的相应位表示为1,其他位表示为0。设低阻故障为第三类故障,则第三位为1,其他位为0,因此,对应的标签表示为$y=[0,0,1,0]$。其他故障类型采用相同的方法进行故障样本与标签之间的对应,以便模型进行监督性的学习。

不同的电气量的数量级具有差异性,因此有必要对数据样本进行归一化处理,一方面是为了提高数据之间的可比性,以防止训练梯度爆炸;另一方面是为了加快训练速度和提高训练准确率。对于故障量在特定数据范围内波动,采用最大值-最小值标准化方法,使故障量大小降落到[0, 1]。

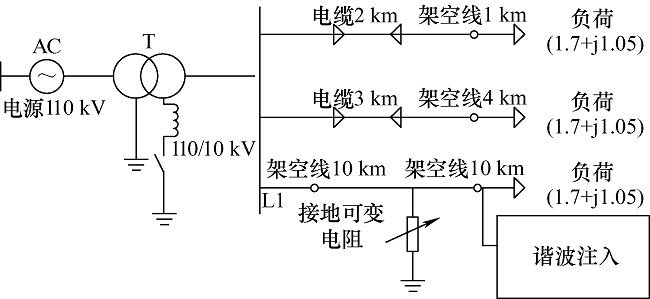
运用PSCAD搭建10 kV配电网经典模型如图3所示。配电网模型主要涵盖变压器、架空线路、电缆线路、谐波注入模块以及负荷等,其中主变压器高低压侧变比为110/10 kV,低压侧中性点接地方式根据可控开关分为中性点不接地和中性点经消弧线圈接地两种方式。架空线路和电缆的参数值如表3所示。本文主要呈现较复杂的电弧接地和非线性高阻接地故障仿真。

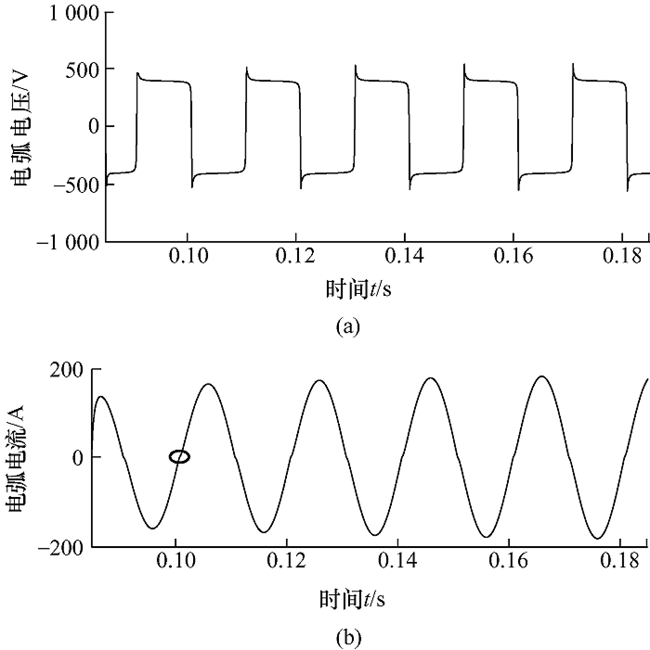
(1) 通过自定义组件搭建电弧模型,设置关键参数,以A相接地故障为例,仿真出电弧电压、电弧电流如图4所示。

由图4a可知,发生电弧接地故障时,电弧电压不再按照正弦波的形式变化,出现明显畸变,呈“马鞍型”。由图4b中的小圆圈可知,电弧电流在过零时,在过零点前后阶段出现“零休”现象,此阶段电流并不按照正弦波变化,而是按电弧电压与电弧阻值的比值变化。另外由于此阶段电流过零,电弧短暂熄灭,电弧电阻呈现高阻状态。因此,在发生单相电弧接地故障时,因为电弧反复熄灭、重燃过程中,接地电阻在不断发生改变,造成故障信息呈现间歇性。

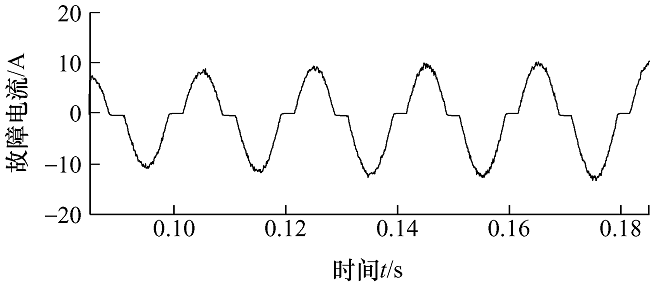
(2) 配电网发生非线性高阻接地故障的仿真,采用经典的伊曼纽尔模型。根据搭建的10 kV配电网模型,进行A相非线性高阻接地仿真,仿真结果故障点电流如图5所示。

由图5可知,仿真结果能够很好地反映非线性高阻接地故障特点。故障点处电流呈现间歇性且幅值大小不一。

本文仿真试验在个人计算机(Windows 10,内存8 GB,CPU 2.4 GHz)上完成。CNN采用Python 3.5.2和TensorFlow深度学习框架搭建,TensorFlow-GPU版本为1.14.0。SVM采用Sklearn库搭建,scikit-learn版本为0.21.3。

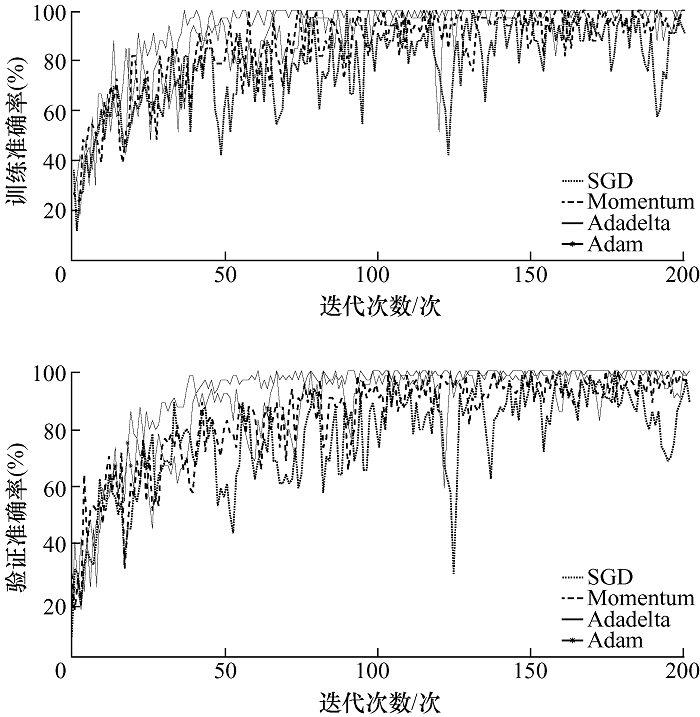
将训练集和验证集样本批量喂入CNN模型,一次批量分别喂入64个和32个故障样本,迭代200次,并采用SGD算法、Momentum算法、自适应Adadelta和Adam四种优化算法对训练结果进行对比。四种算法训练准确率和验证准确率如图6所示。

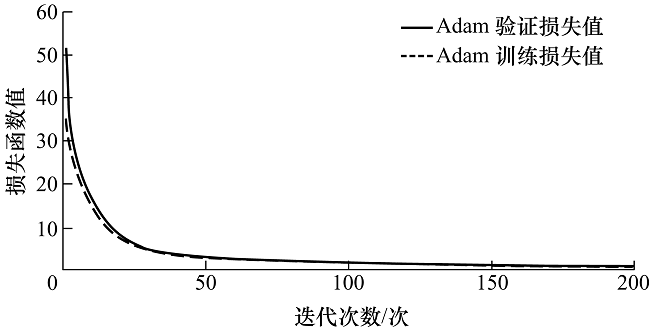
从图6可以看出,采用SGD算法训练准确率和验证准确率波动都较大,收敛效果不好。Momentum算法较SGD算法波动减小,准确率有所提升。Adadelta算法准确率在后期比Momentum表现更好,但在收敛附近出现了几次明显的抖动,稳定性不足。Adam算法收敛速度最快,训练准确率和验证准确率波动较小。另外,CNN在正则化约束和Adam算法相结合下,训练损失和验证损失同步稳定下降,泛化性能好,如图7所示。因此,综合以上优先选择Adam作为Loss值下降优化 算法。

同样搭建MLP(Multi-layer perceptron)、支持向量机(Support vector machine, SVM)^[13]两种模型,与CNN模型进行对比。MLP含有两层隐含层,每一层隐含层包含256个神经单元,其他优化过程和参数与CNN一样,采用L2正则化,惩罚系数为0.000 1,dropout=0.5,激活函数采用ReLU,权重优化为Adam算法,迭代次数为200次。

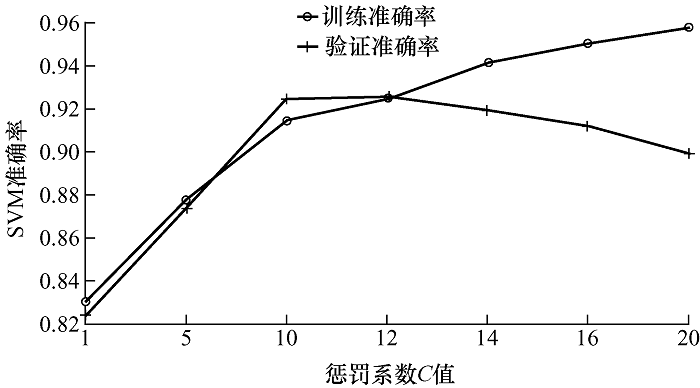
由于SVM输入数据必须为一维矢量,而直接将故障信息矩阵转换为一维矢量,产生的维度较高,造成SVM训练困难。因此,先采用t-SNE方法对故障信息矩阵进行降维。为了保证SVM模型最优,采用径向基核函数,惩罚系数分别设置为C=1,5,10,12,14,16,20,使用网格搜索法寻优。SVM训练和验证准确率结果如图8所示。

从图8可知,随着惩罚系数C值增加,训练准确率和验证准确率不断提高,但在惩罚系数C值过大时,验证准确率反而出现了下降,表明此时SVM模型发生了过拟合。结合训练准确率和验证准确率,选取惩罚系数为12,以获得SVM最优训练模型。

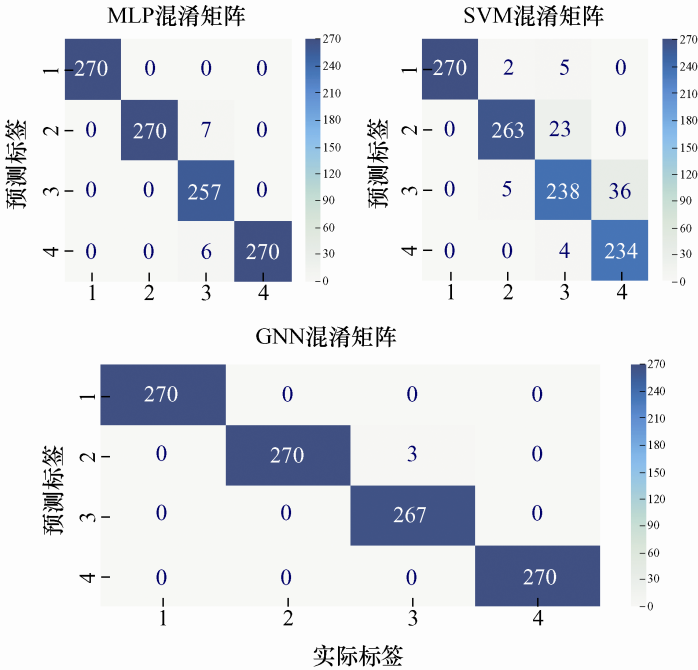
将全部测试集样本一次性喂入训练好的MLP、SVM、CNN模型中,根据每一种模型测试结果,生成相应混淆矩阵,如图9所示。图9中横纵坐标的数字1、2、3、4分别代表间歇性电弧、稳定性电弧、线性低阻和非线性高阻四种故障类型,其中横坐标为实际故障类型,纵坐标为预测故障类型。由于是多类识别问题,根据统计学知识,给出四类故障准确率与F1值的平均值作为模型评估指标,评估结果如表4所示。

从表4可以看到,CNN模型识别效果最好,准确率达到99.72%。SVM模型较CNN低了6.66%,识别效果不佳。MLP模型的准确率达到98.80%,但与CNN还有一定的差距。从F1综合指标来看,CNN的F1值和准确率保持一样,而SVM、MLP的F1值较准确率指标出现了些微下降。

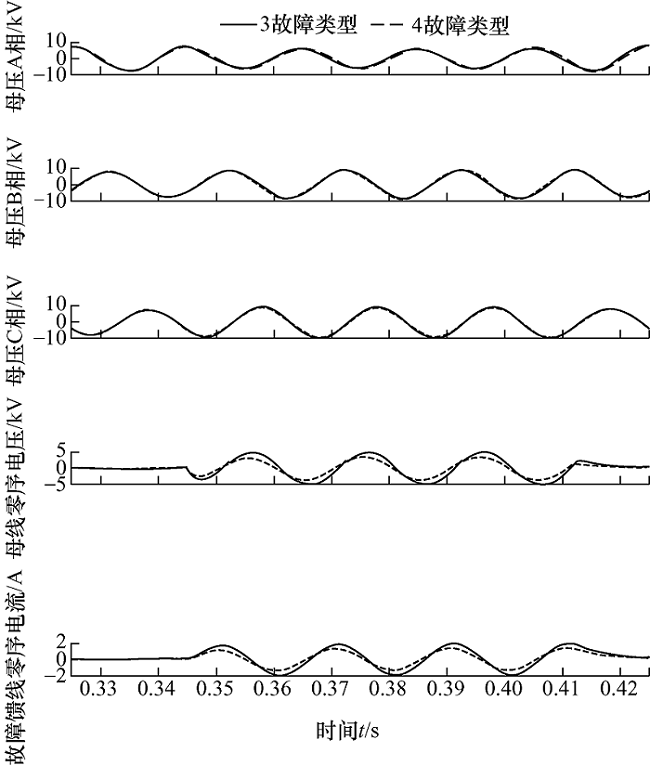
由于配电网的故障识别在于所有的故障都能正确被识别,以免错判,影响电网下一步动作。因此,在识别中更加关注的是正确的标签数据中识别正确的数量的比率,即混淆矩阵中的每一列所对应的情况。如图9所示,SVM模型识别效果整体表现太差,2、3、4故障类型之间错判的数量较多,无法很好地满足实际电网故障识别准确率的要求。MLP模型在直接面对底层数据(数据大小为1 000$\times $5)上表现较SVM更好。而出现的少量故障错判,集中表现在将3故障类型识别为2、4故障类型。以其中一个识别错误的3故障类型样本为例进行分析,比较了识别错误的3故障类型与对应编号的4故障类型的相似性,结果如图10所示。

从图10可知,3故障类型与4故障类型在底层数据上较接近,MLP难以挖掘有效故障特征,造成识别困难。另外,通过大量试验分析,3故障类型和4故障类型的频率特征有着较大的差异。因此,可利用小波变换提取故障量的频率特征,并再结合底层数据,即在这两者数据共同作用下来训练MLP模型,但同时也会增加模型的计算量。

CNN模型通过卷积和池化运算,自动提取底层数据的特征,无需添加额外的故障特征,并且较前几种模型识别错误数量更少,总体识别精度更高。

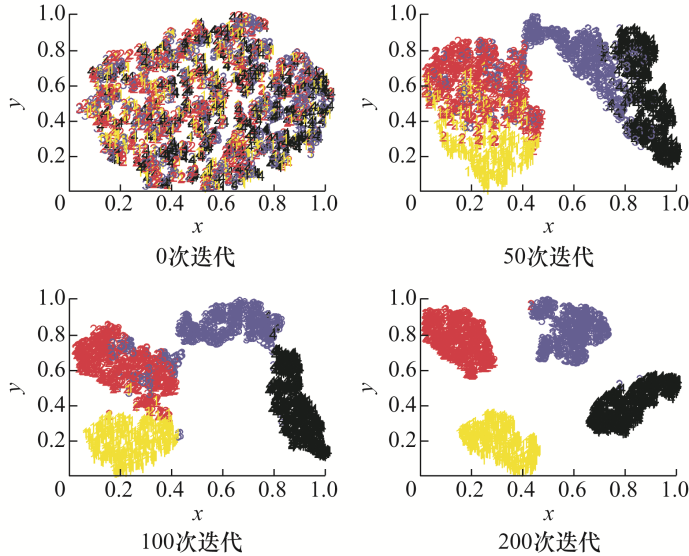
为了分析CNN提取故障特征的过程,本文选取四类故障共2 160个样本。采用t-SNE对CNN迭代次数在0、50、100、200下的全连接层输出结果分别降维到四个x-y二维平面上,并归一化到[0, 1]。结果如图11所示。

从图11可以看出,随着迭代次数的增加,CNN具有良好的自动提取故障特征的能力,四种故障类型逐渐分开,同时也进一步展现了CNN模型优越的识别性能。

本文所提出的方法与文献[5,6,7]进行了对比,结果如表5所示。

由表5可见,所提方法测试效果明显好于文 献[5-7]。本文利用卷积和池化层提取了完整的故障特征,避免了网络退化问题,鲁棒性能更好。

配电网采集装置大多安装于户外,在遭受环境污染以及电力电子装置、通信设备等干扰下,可能会造成采集数据的丢失^[14-15]。因此,有必要考虑模型对所用故障信息的容错能力。

采用Matlab对原始测试集故障信息分别做两次数据丢失,产生两个新的测试数据集。一类是对原始测试样本中的零序电压数据随机丢失2%,另一类是对原始测试样本中的馈线零序电流数据随机丢失2%。为了方便模型测试,以原始测试样本输入模型的矩阵大小为基准,对丢失后不足的故障量序列长度在末尾补0,以保证和原始测试样本大小一样。同样调用训练好的各识别模型,在两个新的测试集上分别做测试,得出准确率、F1值如表6与7所示。

从表6和7整体上来看,零序电压的信息丢失比馈线零序电流信息丢失对各模型的识别性能影响更加严重。不管在零序电压还是零序电流信息丢失下,SVM 识别准确率都出现了较大幅度的下降,模型普适性较差。MLP下降幅度有所减小,但下降幅度也在1%左右。而CNN模型的识别准确率受故障信息丢失影响较小,最终测试准确率依然在99%左右。结合F1值,CNN依然最高。在配电网采集数据可能发生丢失的情况下,CNN模型依然最好,具有较强的容错性。

配电网在新能源、储能装置等接入下,会向其中注入大量的谐波。因此,考虑配电网在谐波注入的情况下,测试模型的识别性能。假设谐波注入相为A相,注入幅值大小为0.1 kA,注入的频率为50~100 Hz。在不同的负荷、电压、频率、接地电阻下,一共仿真360个在注入谐波下的测试样本。采用SVM、MLP、CNN模型对此样本进行测试,结果如表8所示。

从表8可以看出,在注入谐波的情况下,SVM、MLP识别准确率受到较大的影响,出现了10%的下降,而CNN识别准确率和F1指标依然在94%以上。CNN模型受谐波的影响更小,能够很好地应对电力系统谐波干扰。

(1) 运用PSCAD仿真软件完成四种单相接地故障类型的仿真,并构建海量故障样本集及标签。

(2) 搭建CNN模型,并采用正则化处理和Adam优化算法,通过与传统机器学习算法SVM、MLP进行了对比,CNN的识别准确率最高,达到99.72%。

(3) 采用t-SNE对故障样本进行降维、聚类,做出二维可视化散点图,展现了CNN自动提取故障特征的能力。

(4) 在配电网故障信息丢失以及注入谐波的情况下,验证了CNN的容错性和鲁棒性。