1 引言
随着能源需求的不断增长,化石能源的日益消耗,以风能、太阳能为主的可再生能源在发电系统中得到了较为广泛的应用,但风光发电易受周围环境因素的影响,具有波动性和可间断性的特点[1 -3 ] 。此外,风光发电的成本与收益问题也极大影响其在电力系统中的应用。因此,对含风光机组小型发电系统的可靠性与经济性评估研究具有重要意义。
目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] 。文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估。文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响。文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性。文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估。文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估。文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性。上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响。文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电。
综上所述,为了更好地评价含风光机组的小型发电系统可靠性及经济性,本文在首先考虑风电机组三状态停运模型及光伏发电机组双状态停运模型的基础上,建立了风光机组的可靠性评估模型,其次基于序贯蒙特卡洛法对不同风/光装机容量及配置比例情况下的可靠性指标进行计算,最后将可靠性评估中得到的负荷缺电量量化为可靠性成本,结合系统固有成本建立综合成本函数,并在考虑环保收益及节省燃料收益的情况下,对含风光机组的小型发电系统进行经济性评估。
2 风光发电系统可靠性评估模型
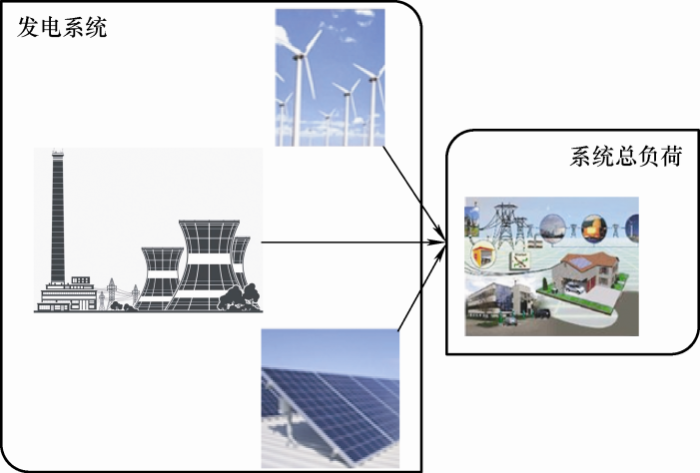
在发电系统可靠性评估中可分为孤立系统和互联系统两大类,本文考虑包括传统发电、风力发电和太阳能发电的孤立发电系统,含风光发电的孤立发电系统如图1 所示。当系统发电功率大于等于系统总负荷时为可靠状态,否则为不可靠状态[11 -12 ] 。由于本文中系统发电功率包括风/光互补发电系统及常规机组的出力,因此在风光发电系统可靠性评估模型中需要建立风电机组及光伏机组出力模型。
图1
2.1 风电机组出力模型
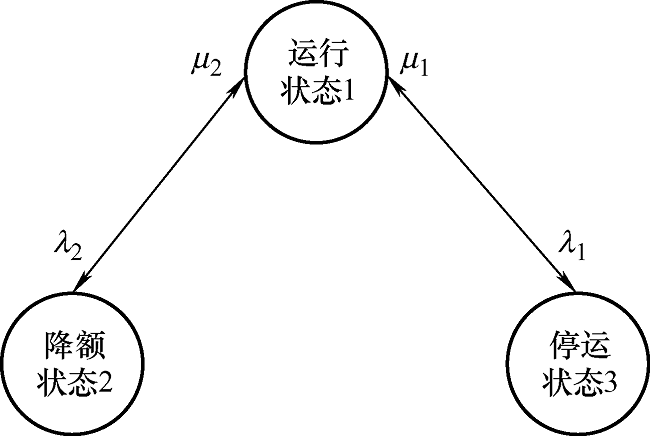
基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] 。通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化。风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] 。
图2
图2 中,${{\lambda }_{1}}$为风机停运状态的转移率;${{\lambda }_{2}}$为风机降额状态的转移率;${{\mu }_{1}}$和${{\mu }_{2}}$为修复率,其单位均是次/年,采用蒙特卡洛法对风机三状态进行随机抽样。
(1) ${{\tau }_{12}}\text{=}-\frac{1}{{{\lambda }_{2}}}\ln {{\gamma }_{12}}$
(2) ${{\tau }_{13}}\text{=}-\frac{1}{{{\lambda }_{1}}}\ln {{\gamma }_{13}}$
(3) ${{\tau }_{21}}\text{=}-\frac{1}{{{\mu }_{2}}}\ln {{\gamma }_{21}}$
(4) ${{\tau }_{31}}\text{=}-\frac{1}{{{\mu }_{1}}}\ln {{\gamma }_{31}}$
式中,${{\tau }_{12}}$、${{\tau }_{13}}$分别为状态1未进入状态2前及状态1未进入状态3前,状态1运行的持续时间;${{\tau }_{21}}$、${{\tau }_{31}}$分别为降额与停运故障修复时间;${{\gamma }_{12}}$、${{\gamma }_{13}}$、${{\gamma }_{21}}$、${{\gamma }_{31}}$分别为[0,1]内的均匀分布随机数。
基于预测风速${{v}_{t}}$,采用分段函数表示风电机组输出功率[16 -17 ] ,并在考虑风机三状态空间模型的情况下得到最终风电机组输出功率。
(5) ${{p}_{ti}}=\left\{ \begin{array}{*{35}{l}} 0 & 0\le {{v}_{t}}\le {{v}_{ci}} \\ (\alpha +\beta {{v}_{t}}+\gamma v_{t}^{2}){{p}_{r}} & {{v}_{ci}}\le {{v}_{t}}\le {{v}_{r}} \\ {{p}_{r}} & {{v}_{r}}\le {{v}_{t}}\le {{v}_{co}} \\ 0 & {{v}_{t}}\ge {{v}_{co}} \\ \end{array} \right.$
式中,${{p}_{ti}}$为每台风机$t$时刻的实时出力;${{p}_{r}}$为风机额定功率;${{v}_{ci}}{{v}_{r}}{{v}_{co}}$分别为风机的切入风速、额定风速及切出风速;$\alpha \beta \gamma $分别为风电机组功率特性曲线的待定系数[18 ] 。
2.2 光伏机组出力模型
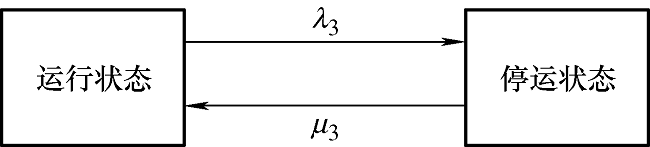
光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] 。因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示。
图3
图3 中,${{\lambda }_{3}}$为光伏发电机组停运状态的转移率;${{\mu }_{3}}$为修复率;运行持续时间${{\tau }_{3}}$及停运故障修复时间${{\tau }_{4}}$分别如式(6)、(7)[22 ] 所示。
(6) ${{\tau }_{3}}\text{=}-\frac{1}{{{\lambda }_{3}}}\ln {{\gamma }_{3}}$
(7) ${{\tau }_{4}}\text{=}-\frac{1}{{{\mu }_{3}}}\ln {{\gamma }_{4}}$
式中,${{\gamma }_{3}}$和${{\gamma }_{4}}$为[0,1]内的均匀分布随机数。
基于由Homer软件生成的光辐照度实时序列,采用分段函数表示光伏发电机组的输出功率[23 ] ,并在考虑光伏双状态空间模型的情况下得到最终光伏发电机组输出功率。
(8) ${{p}_{tj}}=\left\{ \begin{array}{*{35}{l}} {{p}_{sn}}\{G_{bt}^{2}/({{G}_{std}}{{R}_{c}})\} & 0\le {{G}_{bt}}<{{R}_{c}} \\ {{p}_{sn}}({{G}_{bt}}/{{G}_{std}}) & {{R}_{c}}\le {{G}_{bt}}<{{G}_{std}} \\ {{p}_{sn}} & {{G}_{std}}\le {{G}_{bt}} \\ \end{array} \right.$
式中,${{p}_{tj}}$为每组光伏机组$t$时刻的实时出力;${{p}_{sn}}$为光伏额定功率;${{R}_{c}}$为光伏出力从非线性到线性转变过程中的某一特定光强;${{G}_{std}}$为额定光强;${{G}_{bt}}$为光辐照度实时序列。
3 经济性评估模型
3.1 成本模型
在计及可靠性的含风光机组小型发电系统经济性评估中,综合成本模型主要包括系统的运行与投资成本、可靠性成本,其函数表达如式(9) 所示
(9) ${{y}_{z}}={{y}_{w}}+{{y}_{s}}+{{y}_{g}}+{{y}_{k}}$
式中,${{y}_{z}}$为综合成本;${{y}_{w}}$为风力发电机组总成本;${{y}_{s}}$光伏发电机组总成本;${{y}_{g}}$为常规发电机组总成本;${{y}_{k}}$为可靠性成本。
(10) ${{y}_{w}}=\sum\limits_{i=1}^{W}{\left[ \sum\limits_{t=1}^{8\ \ 760}{{{p}_{i}}}(t)\times \left( {{Z}_{i}}\frac{{{r}_{0}}{{(1\text{+}{{r}_{0}})}^{m}}}{{{(1\text{+}{{r}_{0}})}^{m}}-1}+{{X}_{i}} \right) \right]}$
式中,${{p}_{i}}(t)$为每台风力发电机组的当前时刻出力;$W$为风力发电机组的台数;${{r}_{0}}$为风电机组的贴现率;$m$为风电机组的折旧年限;${{Z}_{i}}$为第$i$台风力发电机组的单位千瓦时投资(其中单位千瓦时投资指的是电站总投资与电站设计年发电量的比值);${{X}_{i}}$为每台风力发电机组的单位运行与维护成本。
(11) ${{y}_{s}}=\sum\limits_{j=1}^{S}{\left[ \sum\limits_{t=1}^{8\ \ 760}{{{p}_{j}}}(t)\times \left( {{Z}_{j}}\frac{{{r}_{1}}{{(1+{{r}_{1}})}^{n}}}{{{(1+r)}^{m}}-1}+{{X}_{j}} \right) \right]}$
式中,${{p}_{j}}(t)$为每组光伏发电机组的当前时刻出力;$S$为光伏发电机组的数量;${{r}_{1}}$为光伏发电机组的贴现率;$n$为光伏发电机组的折旧年限;${{Z}_{j}}$为第$j$组光伏发电机组的单位千瓦时投资;${{X}_{j}}$为每组光伏发电机组的单位运行与维护成本。
(12) $\begin{matrix} {{y}_{g}}= \sum\limits_{G=1}^{N}{\left\{ {{\left[ a\left( \sum\limits_{t=1}^{8\ 760}{{{p}_{G}}(t)} \right) \right]}^{2}}+b\sum\limits_{t=1}^{8\ 760}{{{p}_{G}}(t)}+c+\sum\limits_{t=1}^{8\ 760}{{{p}_{G}}(t)}({{Z}_{G}}+{{X}_{G}}) \right\}} \\ \end{matrix}$
式中,$N$为常规发电机的台数;${{p}_{G}}(t)$为每台常规机组的当前时刻出力;$abc$为燃料成本函数系数;${{Z}_{G}}$为常规发电机组的单位千瓦时投资;${{X}_{G}}$为每台常规机组的单位运行与维护成本。
(4) 可靠性成本函数,即在可靠性评估过程中因负荷缺电量造成的成本费用[24 ] 的函数表达式为
(13) ${{y}_{k}}=K{{p}_{loss}}$
式中,$K$可靠性赔偿系数;${{p}_{loss}}$为电量缺失造成的功率损失;$K$、${{p}_{loss}}$的计算公式分别如式(14)、(15)所示
(14) $K={{b}_{1}}R+{{b}_{2}}ae$
式中,${{b}_{1}}{{b}_{2}}$为加权平均系数;$R$为产电比;a 为电价倍数;e 为平均电价。
(15) ${{p}_{loss}}=\sum\limits_{t=1}^{\text{8}\ \ \text{760}}{\{{{p}_{load}}(t)-[{{p}_{w}}(t)+{{p}_{s}}(t)+{{p}_{g}}(t)]\}}R(t)$
式中,${{p}_{load}}(t)$、${{p}_{w}}(t)$、${{p}_{s}}(t)$、${{p}_{g}}(t)$分别为当前时刻的需求负荷、风力发电机组总出力、光伏发电机组总出力及常规发电机组总出力;$R(t)$为缺电系数,其计算公式如下所示
(16) $R(t)=\left\{ \begin{matrix} 0 & {{p}_{w}}(t)+{{p}_{s}}(t)+{{p}_{g}}(t)\ge {{p}_{load}}(t) \\ 1 & {{p}_{w}}(t)+{{p}_{s}}(t)+{{p}_{g}}(t)<{{p}_{load}}(t) \\ \end{matrix} \right.$
3.2 收益模型
在计及可靠性的含风光机组小型发电系统经济性评估中,综合收益模型主要考虑减少温室气体的减排效益及节约燃料带来的收益,且在收益模型中忽略弃风弃光的影响。
(17) ${{N}_{s}}={{N}_{j}}+{{N}_{r}}$
式中,${{N}_{s}}$为综合收益;${{N}_{j}}$为减少温室气体带来的收益;${{N}_{r}}$为节约燃料带来的收益。
减少温室气体的减排效益带来的效益主要由通过风力及光伏发电减少CO2 、CO、SO2 、NOBX B 这四类温室气体排放带来的效益,在此假设采用风力及光伏发电完全不会产生任何温室气体且其出力原本应由常规机组输出,减排收益模型如下所示
(18) ${{W}_{q}}={{S}_{\text{C}{{\text{O}}_{\text{2}}}}}{{P}_{\text{C}{{\text{O}}_{\text{2}}}}}+{{S}_{\text{CO}}}{{P}_{\text{CO}}}+{{S}_{\text{S}{{\text{O}}_{\text{2}}}}}{{P}_{\text{S}{{\text{O}}_{\text{2}}}}}+{{S}_{\text{N}{{\text{O}}_{X}}}}{{P}_{\text{N}{{\text{O}}_{X}}}}$
(19) ${{N}_{j}}=\sum\limits_{t=1}^{8\ \ 760}{[{{p}_{w}}(t)+{{p}_{s}}(t)]}\times {{W}_{q}}$
式中,${{S}_{\text{C}{{\text{O}}_{\text{2}}}}}{{S}_{\text{CO}}}{{S}_{\text{S}{{\text{O}}_{\text{2}}}}}{{S}_{\text{N}{{\text{O}}_{X}}}}$分别为常规机组生产单位电能排放CO2 、CO、SO2 、NOBXB 2 、CO、SO2 、NOBXB 这四类温室气体所需的单价。
(20) ${{N}_{r}}=\frac{\sum\limits_{t=1}^{8\ \ 760}{[{{p}_{w}}(t)+{{p}_{s}}(t)]}}{rl}\times {{p}_{d}}$
式中,$rl$为热耗率;${{p}_{d}}$为燃料价格。
4 评估流程及相关参数设置
4.1 评估流程图
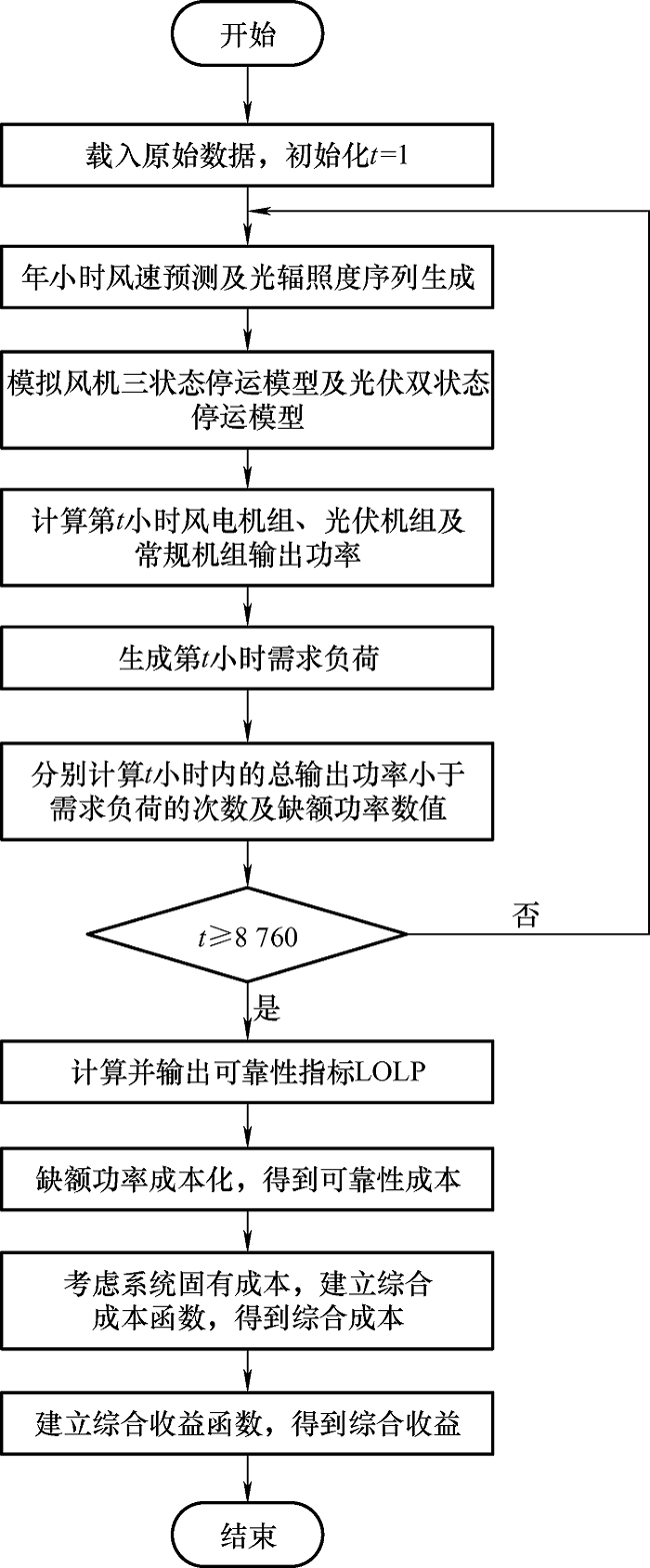
首先载入历史风速数据,采用时间序列模型对未来一年8 760 h的风速进行预测,采用Homer软件生成一年8 760 h的光辐照度数据,采用三状态停运模型及双状态停运模型分别模拟风/光机组停运状态。基于上述模型及基础数据采用风/光出力函数输出一年8 760 h的风/光出力,生成一年8 760 h的模拟负荷,分别计算t 小时内的总输出功率小于需求负荷的次数及负荷缺电量数值,将负荷缺电量量化为可靠性成本,在计及系统固有成本的前提下,建立综合成本函数。最后从不同装机容量及风/光配置比例对系统可靠性的影响、对可靠性成本的影响、对综合成本的影响及对综合收益的影响四个方面进行综合分析,得到最优规划方案。基本流程如图4 所示。
图4
图4
计及可靠性的含风光机组小型发电系统经济性评估流程图
4.2 相关参数设置
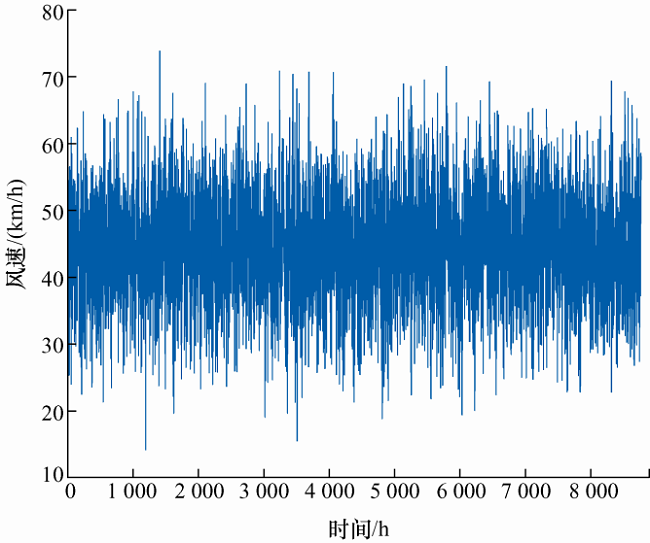
本文中风力发电机切入风速为20 km/h、额定风速为41 km/h、切出风速为66 km/h、额定功率为1 kW[9 ] ,采用自回归滑动模型模拟出的一年逐时风速数据,如图5 所示。风机的三状态转移率分别取λ 1 =7.96次/年、λ 2 =5.84次/年、μ 1 =58.4次/年、μ 2 =48.3次/年,假设风机降额功率为正常输出功率的0.8倍。
图5
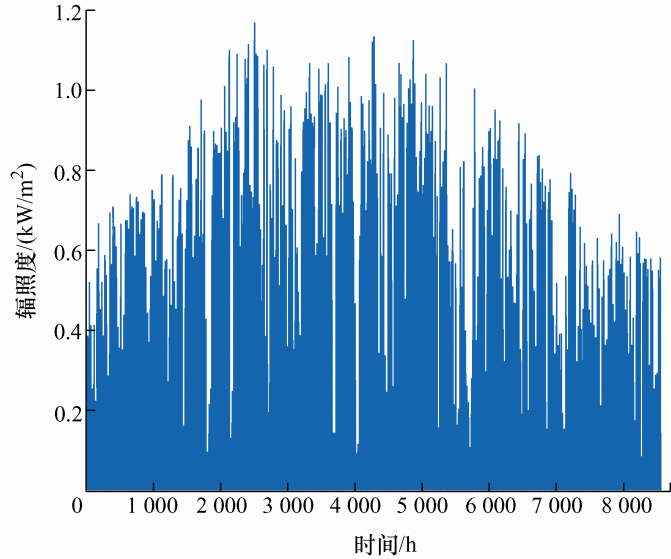
光伏发电机组的额定功率${{p}_{sn}}$取1 kW,额定光强${{G}_{std}}$取1 kW/m2 ,某一特定光强${{R}_{c}}$取0.15 kW/m2 ,光伏发电机组的双状态转移率${{\lambda }_{3}}{{\mu }_{3}}$分别取 10.84次/年、48.3次/年,光辐照度数据如图 6 所示[9 ] 。
图6
图7
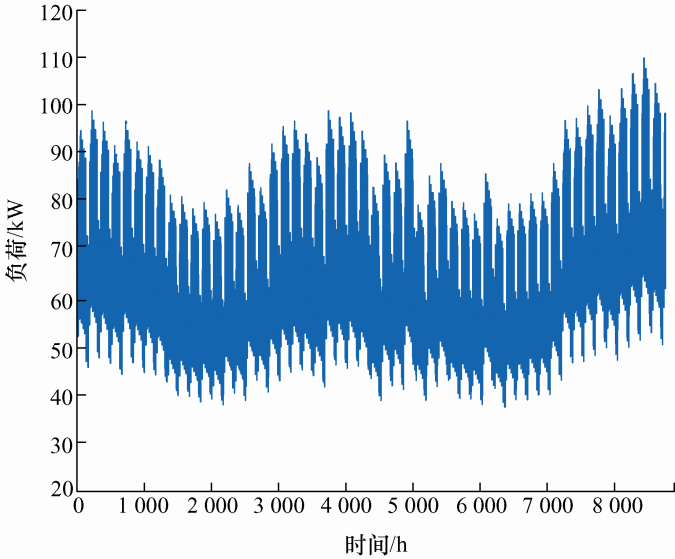
假设常规发电机组的额定功率为10 kW,系统中常规发电机组的台数为11台,每台常规机组的强迫停运率统一取成4%,一年逐时负荷数据如图 7 所示,系统峰荷为110 kW。
风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h。假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示。
5 算例分析
5.1 含风光机组的小型发电系统可靠性评估
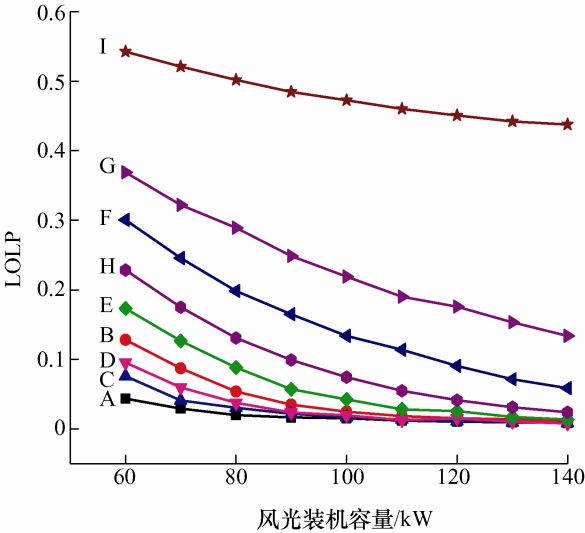
在含风光机组的小型发电系统可靠性评估中,为了评估不同风/光比例及装机容量对系统可靠性的影响,风/光装机容量从60 kW到140 kW等步增加并将风/光比例分为1:0、3:2、4:1、7:3、1:1、3:7、1:4、2:3、0:1这九种情况对可靠性进行评估,计算可靠性指标(Loss of load probability,LOLP),数值越小代表系统越可靠,不同风/光比例及装机容量对系统可靠性的影响如图8 所示。图8 中A~I依次分别表示为风/光配置比例为1:0、3:2、4:1、7:3、1:1、3:7、1:4、2:3、0:1的情况。
图8
由图8 可以看出,随着风/光装机容量的增加,LOLP的数值逐渐减小,系统的可靠性逐渐提高。当风/光装机容量增大到100 kW时,对于A、B、C、D、E这五种配置方式而言继续增加装机容量LOLP的数值变化幅度不大,并且随着装机容量的增加,这五种配置方式的可靠性数值呈现出相接近的趋势,表明系统中配置较高比例的风电时,在风/光装机容量达到一定数值后继续增加装机容量对提升系统整体可靠性的影响并不显著。随着装机容量的逐渐增加,光伏发电占比较高的系统(F风/光比例为3:7,G风/光比例为1:4,H风/光比例为2:3)可靠性提升速率则较为明显,但仅仅只配置光伏电场(I风/光比例为0:1)的可靠性提升速率较F、G、H而言则较为缓慢。在风/光装机容量一定时,随着风电比例的增加,系统的可靠性也逐渐提升,其中风/光接入比例为1:0时系统的可靠性最高。
5.2 计及可靠性的含风光机组小型发电系统经济性 评估
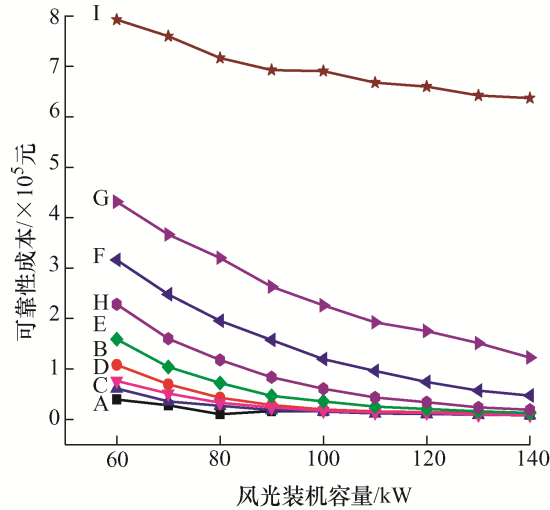
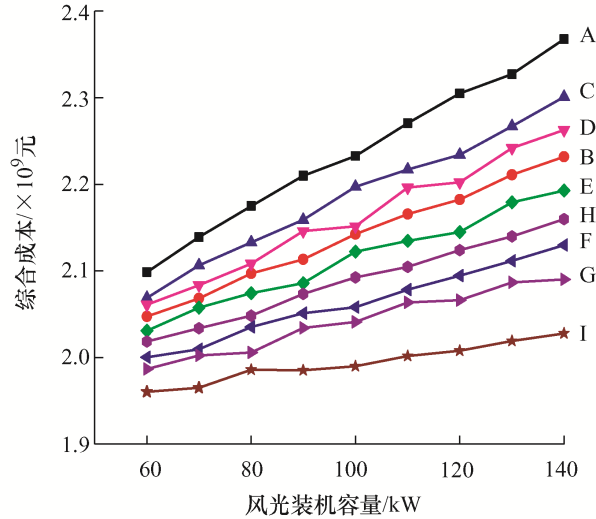
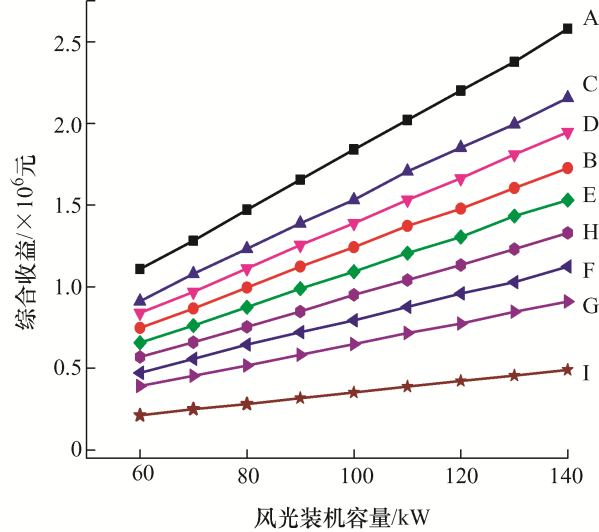
在计及可靠性的含风光机组小型发电系统经济性评估中,为了评估不同风/光比例及装机容量对系统经济性的影响,计算不同风/光比例、不同风光装机容量情况下的风力发电成本、光伏发电成本、可靠性成本、综合成本及综合收益。图9 为不同风/光比例及装机容量对可靠性成本的影响;图10 为不同风/光比例及装机容量对综合成本的影响;图11 为不同风/光比例及装机容量对综合收益的影响。在图9 ~11 中A~I均依次分别表示风/光配置比例分别为1:0、3:2、4:1、7:3、1:1、3:7、1:4、2:3、0:1的情况。
图9
图10
图11
由于可靠性成本是通过量化负荷缺电量而带来的损失而得。因此,由图9 可以看出其变化趋势与图8 中的可靠性指标LOLP的变化趋势相接近,风/光配置比例为0:1的系统可靠性成本最高。对于A、B、C、D、E、H这六种配置方式而言,当风/光装机容量达到一定数值后,再增加风/光装机容量对降低可靠性成本数值的作用并不明显。
由图10 可以看出,综合成本与风/光装机容量成正比关系,随着风/光装机容量的增加综合成本也逐渐增加。在风/光装机容量分别为60 kW、70 kW、80 kW的前提下,A、B、C、D、E、F、G、H、I的综合成本相差不大,但当逐渐提升装机容量时会导致综合成本的差距逐渐变大。光伏占比高的系统综合成本相对而言较低,其中风/光配置比例为0:1的系统综合成本最低,风/光配置比例为1:0的系统综合综合成本则最高。
由图11 可以看出,在相同风/光装机容量的条件下,风/光比例为1:0时的综合收益最高且增长速率最快,风/光比例为0:1时的综合收益最低且增长速率最慢。随着风/光装机容量的增加,各配置比例所得到的综合收益差距也在拉大。
综合图8 ~11的仿真数据可知,尽管接入高比例的风力发电机组可以提高系统整体的可靠性,降低可靠性成本,增加综合收益,但是综合成本却相对较高;而接入高比例的光伏发电机组综合成本相对较低,但是系统整体的可靠性却较差,并且综合收益也较低,这是由于风力发电的单位造价及运维成本要高于光伏发电系统,而同等装机容量的风电出力要比光伏出力更加稳定造成的。随着风/光装机容量的不断增加,系统的可靠性提高,可靠性成本下降,综合收益上升,综合成本也随着上升。当风/光装机容量达到100 kW后再继续增加装机容量,对于风电占比较高的系统而言可靠性提升效果并不明显,对于光伏占比较高的系统而言可靠性提升速率也逐渐缓慢。
因此,本文在综合考虑可靠性、可靠性成本、综合成本及综合收益的前提下,选用风/光装机容量为100 kW且风/光配置比为3:2、7:3、1:1、3:7、2:3的这几种配置方式较为经济可靠。
6 结论
本文在考虑风电机组三状态停运模型及光伏发电机组双状态停运模型的基础上,采用序贯蒙特卡洛法对不同风/光装机容量及不同风/光配置比例情况下的发电系统可靠性进行评估,并在考虑综合成本及综合收益的情况下,分析了系统的经济性。本文所提方法可为含风光机组小型发电系统的系统规划提供一定的参考,并且通过本文的所取的相关参数数值及算例分析得到如下结论。
(1) 系统的可靠性随着风/光装机容量的逐渐增加而提高,但当装机容量增加到一定程度时,部分风/光比例配置方案下的可靠性数值呈现出相接近的趋势。
(2) 在风/光装机容量一定时,随着风电比例的增加,系统的可靠性也逐渐提升,这是由于夜晚无光辐照度造成光伏发电机组无出力导致的,与实际情况基本吻合。
(3) 对含风光机组的小型发电系统较只含单一的风或光的小型发电系统而言,能在保证系统具有良好可靠性的前提下减少系统的综合投资成本且能使系统获得较为可观的综合收益。
(4) 系统可靠性及综合收益随着风/光装机容量的不断增加也随之不断提升,但增加装机容量的同时综合成本也随之增加,且综合成本增加数值远大于综合收益。因此,合理配置风/光装机容量能在保证系统可靠性的前提下节约投资费用。
参考文献
View Option
[1]
刘邓 , 张丹 , 周怡 , 等 . 集中式与集散式光伏发电系统MPPT的仿真与对比
[J]. 电气工程学报 , 2018 ,13 (10 ):41 -46 .
[本文引用: 1]
LIU Deng ZHANG Dan ZHOU Yi , et al . Simulation and comparison of centralized and distributed photovoltaic power generation system on MPPT
[J]. Journal of Electrical Engineering , 2018 ,13 (10 ):41 -46 .
[本文引用: 1]
[2]
吴红斌 , 白雪 , 王蕾 . 基于序贯蒙特卡洛模拟的风光储发电系统可靠性评估
[J]. 太阳能学报 , 2017 ,38 (6 ):1501 -1509 .
WU Hongbin BAI Xue WANG Lei . Reliability evaluation of wind-solar-battery generation system based on sequential Monte Carlo simulation
[J]. Acta Energiae Solaris Sinica , 2017 ,38 (6 ):1501 -1509 .
[3]
程临燕 , 冯艳虹 , 徐林 . 基于风光互补出力特性的可消纳容量研究
[J]. 中国电力 , 2019 ,52 (7 ):63 -68 .
[本文引用: 1]
CHENG Linyan FENG Yanhong XU Lin . Consumptive capacity research based on wind-solar hybrid charac- teristics
[J]. Electric Power , 2019 ,52 (7 ):63 -68 .
[本文引用: 1]
[4]
HUANG D G BILLINTON R . Effects of wind power on bulk system adequacy evaluation using the well-being analysis framework
[J]. IEEE Transactions on Power Systems , 2009 ,24 (3 ):1232 -1240 .
DOI:10.1109/TPWRS.2009.2021232
URL
[本文引用: 2]
[5]
栗文义 , 王银莎 , 郭鑫 , 等 . 基于 Well-Being 模型的风力发电系统可靠性评估
[J]. 华东电力 , 2011 ,39 (7 ):1062 -1065 .
[本文引用: 1]
LI Wenyi WANG Yinsha GUO Xin , et al . Reliability evaluation of wind power system based on Well-Being model
[J]. East China Electric Power , 2011 ,39 (7 ):1062 -1065 .
[本文引用: 1]
[6]
刘步中 , 张曦煌 . 基于模糊聚类的含风电场发电系统可靠性分析
[J]. 电网与清洁能源 , 2016 ,32 (7 ):138 -142 .
[本文引用: 1]
LIU Buzhong ZHANG Xihuang . Reliability analysis of generation systems with wind power based on fuzzy clustering
[J]. Power System and Clean Energy , 2016 ,32 (7 ):138 -142 .
[本文引用: 1]
[7]
王敏 , 宗炫君 , 袁越 , 等 . 含光伏电站的发电系统可靠性分析
[J]. 中国电机工程学报 , 2013 ,33 (34 ):42 -49 .
URL
[本文引用: 1]
为分析光伏电站并网对发电系统可靠性的影响,提出了新的光伏电站多状态可靠性模型。模型根据光伏电站实测数据求得各状态的晴空指数和辐照度波动指标,提出按数据等频划分的原则计算各状态之间的转移概率,并对给定状态下的太阳辐照度进行分时模拟,最后采用序贯蒙特卡洛模拟法评估含光伏电站的发电系统的可靠性。由于考虑了实际太阳辐照度波动特性与晴空指数之间的相关性,状态抽样结果表明,提出的光伏辐照度多状态时序模型更符合实际的天气变化特性。基于RBTS的仿真结果表明,采用此模型的光伏电站可靠性分析相对于直接抽样法的计算结果更精确。
WANG Min ZONG Xuanjun YUAN Yue , et al . Reliability analysis of generation systems with photovoltaic stations
[J]. Proceedings of the CSEE , 2013 ,33 (34 ):42 -49 .
URL
[本文引用: 1]
为分析光伏电站并网对发电系统可靠性的影响,提出了新的光伏电站多状态可靠性模型。模型根据光伏电站实测数据求得各状态的晴空指数和辐照度波动指标,提出按数据等频划分的原则计算各状态之间的转移概率,并对给定状态下的太阳辐照度进行分时模拟,最后采用序贯蒙特卡洛模拟法评估含光伏电站的发电系统的可靠性。由于考虑了实际太阳辐照度波动特性与晴空指数之间的相关性,状态抽样结果表明,提出的光伏辐照度多状态时序模型更符合实际的天气变化特性。基于RBTS的仿真结果表明,采用此模型的光伏电站可靠性分析相对于直接抽样法的计算结果更精确。
[8]
赵继超 , 袁越 , 傅质馨 , 等 . 基于Copula理论的风光互补发电系统可靠性评估
[J]. 电力自动化设备 , 2013 ,33 (1 ):124 -129 .
[本文引用: 1]
ZHAO Jichao YUAN Yue FU Zhixin , et al . Reliability assessment of wind-PV hybrid generation system based on Copula theory
[J]. Electric Power Automation Equipment , 2013 ,33 (1 ):124 -129 .
[本文引用: 1]
[9]
应飞祥 , 张恩睦 , 李琰 , 等 . 含风光互补的独立发电系统可靠性评估
[J]. 昆明理工大学学报 , 2019 ,44 (6 ):71 -81 .
[本文引用: 3]
YING Feixiang ZHANG Enmu LI Yan , et al . A reliability assessment of independent power generation system with wind and solar complementation
[J]. Journal of Kunming University of Science and Technology , 2019 ,44 (6 ):71 -81 .
[本文引用: 3]
[10]
BAGEN B BILLINTON R . Reliability cost/worth associated with wind energy and energy storage utilization in electric power systems
[C]// Proceedings of the 10th International Conference on Probablistic Methods Applied to Power Systems. Rincon,IEEE, 2008 : 1 -7 .
[本文引用: 2]
[11]
程林 , 何剑 . 电力系统可靠性原理和应用 [M]. 北京 : 清华大学出版社 , 2015 .
[本文引用: 1]
CHENG Lin HE Jian . Principle and application of power system reliability [M]. Beijing : Tsinghua University Press , 2015 .
[本文引用: 1]
[12]
鲍莎日娜 , 栗文义 , 巴根 , 等 . 风力发电为主导的孤立发电系统可靠性评估
[J]. 电力建设 , 2011 ,32 (7 ):1 -5 .
URL
[本文引用: 1]
针对内蒙古的特定情况,采用以风力发电为主导的小型孤立发电系统提供电能,可保证供电可靠性、节省柴油燃料和保护当地的生态环境。本文所述的小型孤立发电系统以风/柴/储能联合发电的形式提供电能。文章采用序贯Monte-Carlo模拟法实现风/柴/储能发电系统的可靠性评估。根据风电场的风速历史数据,建立风电场的风速时间序列模型。由风速时间序列计算风力发电机的输出功率。在考虑机组随机故障的情况下,由发电机和负荷模型得到蓄电池的时间序列模型。针对样例系统,量化评估了仿真样本容量、蓄电池容量、蓄电池充放电率和风力发电机额定功率等,一些因素对风/柴/储能发电系统可靠性的影响。仿真结果可为风/柴/储能发电系统可靠运行提供依据,为政府及电力部门推广风/柴/储能联合发电向偏远地区供电提供依据。
BAO Sharina LI Wenyi BA Gen , et al . Reliability evaluation of isolated power system generated by wind
[J]. Electric Power Construction , 2011 ,32 (7 ):1 -5 .
URL
[本文引用: 1]
针对内蒙古的特定情况,采用以风力发电为主导的小型孤立发电系统提供电能,可保证供电可靠性、节省柴油燃料和保护当地的生态环境。本文所述的小型孤立发电系统以风/柴/储能联合发电的形式提供电能。文章采用序贯Monte-Carlo模拟法实现风/柴/储能发电系统的可靠性评估。根据风电场的风速历史数据,建立风电场的风速时间序列模型。由风速时间序列计算风力发电机的输出功率。在考虑机组随机故障的情况下,由发电机和负荷模型得到蓄电池的时间序列模型。针对样例系统,量化评估了仿真样本容量、蓄电池容量、蓄电池充放电率和风力发电机额定功率等,一些因素对风/柴/储能发电系统可靠性的影响。仿真结果可为风/柴/储能发电系统可靠运行提供依据,为政府及电力部门推广风/柴/储能联合发电向偏远地区供电提供依据。
[13]
KARKI R HU P BILLINTON R . Reliability evaluation considering wind and hydro power coordination
[J]. IEEE Transactions on Power Systems , 2010 ,25 (2 ):685 -693 .
DOI:10.1109/TPWRS.2009.2032758
URL
[本文引用: 1]
[14]
应飞祥 , 姜燕波 , 何民 , 等 . 含风储系统的电力系统可靠性评估进展与展望
[J]. 智慧电力 , 2019 ,47 (2 ):1 -8,42 .
[本文引用: 1]
YING Feixiang JIANG Yanbo HE Min , et al . Progress and prospect of reliability assessment of power system with wind farm and energy storage system
[J]. Smart Power , 2019 ,47 (2 ):1 -8,42 .
[本文引用: 1]
[15]
蒋程 , 刘文霞 , 张建华 , 等 . 含风电接入的发输电系统风险评估
[J]. 电工技术学报 , 2014 ,29 (2 ):260 -270 .
URL
[本文引用: 1]
考虑风速的随机性、风电机组的功率特性、风机运行条件、风机的降额运行状态、风电场升压变压器和高压输电线路故障率等因素的影响,建立了风电场可靠性模型。针对风电接入情况下传统评估方法样本容量大、效率低等不足,提出了基于分散抽样蒙特卡洛算法的含风电场发输电系统风险评估方法,此抽样算法将[0,1]区间分成若干子区间,在抽样后分别对每个子区间进行系统状态判断和指标计算,从而增加故障状态的抽样频率,提高抽样效率,在满足精度要求下,有效地减少了抽样次数。针对风电的随机性和间歇性等特点,给出了关于风电接入系统的风险指标,该指标能分别反映风电接入对发电系统和输电系统的影响。通过对改进IEEE-RTS79算例的计算分析验证了所提评估方法和指标的有效性。
JIANG Cheng LIU Wenxia ZHANG Jianhua , et al . Risk assessment of generation and transmission system considering wind power penetration
[J]. Transactions of China Electrotechnical Society , 2014 ,29 (2 ):260 -270 .
URL
[本文引用: 1]
考虑风速的随机性、风电机组的功率特性、风机运行条件、风机的降额运行状态、风电场升压变压器和高压输电线路故障率等因素的影响,建立了风电场可靠性模型。针对风电接入情况下传统评估方法样本容量大、效率低等不足,提出了基于分散抽样蒙特卡洛算法的含风电场发输电系统风险评估方法,此抽样算法将[0,1]区间分成若干子区间,在抽样后分别对每个子区间进行系统状态判断和指标计算,从而增加故障状态的抽样频率,提高抽样效率,在满足精度要求下,有效地减少了抽样次数。针对风电的随机性和间歇性等特点,给出了关于风电接入系统的风险指标,该指标能分别反映风电接入对发电系统和输电系统的影响。通过对改进IEEE-RTS79算例的计算分析验证了所提评估方法和指标的有效性。
[16]
王剑 , 刘天琪 , 李兴源 . 风电场及储能装置对发输电系统可靠性的影响
[J]. 电网技术 , 2011 ,35 (5 ):165 -170 .
URL
[本文引用: 1]
随着风电渗透率的逐步增大,针对风电功率的随机性和间隙性,建立了考虑风速时序性和自相关性的自回归–滑动平均风速预测模型,并结合储能装置在电力系统中的应用情况,采用序贯蒙特卡罗仿真方法,分析评估了风电场、储能装置及燃气轮机备用容量对发输电系统可靠性的影响。将风机和储能装置接入IEEE-RTS79系统进行仿真,综合考虑常规机组的强迫停运率、输电元件的故障率、输电网络线路过负荷等因素,仿真结果表明采用该模型和方法能够量化各种因素对发输电组合系统可靠性的影响。
WANG Jian LIU Tianqi LI Xingyuan . Influences of connecting wind farms and energy storage devices to power grid on reliability of power
[J]. Power System Technology , 2011 ,35 (5 ):165 -170 .
URL
[本文引用: 1]
随着风电渗透率的逐步增大,针对风电功率的随机性和间隙性,建立了考虑风速时序性和自相关性的自回归–滑动平均风速预测模型,并结合储能装置在电力系统中的应用情况,采用序贯蒙特卡罗仿真方法,分析评估了风电场、储能装置及燃气轮机备用容量对发输电系统可靠性的影响。将风机和储能装置接入IEEE-RTS79系统进行仿真,综合考虑常规机组的强迫停运率、输电元件的故障率、输电网络线路过负荷等因素,仿真结果表明采用该模型和方法能够量化各种因素对发输电组合系统可靠性的影响。
[17]
孟虹年 , 谢开贵 . 计及电池储能设备运行特性的风电场可靠性评估
[J]. 电网技术 , 2012 ,36 (6 ):214 -219 .
URL
[本文引用: 1]
在含电池储能设备风电场功率时序模型的基础上,建立了含功率型和能量型电池储能设备的风电场可靠性时序评估模型。使用RBTS发电系统作为算例,分析了2类电池设备在不同储能策略下对风电系统可靠性改善的程度,并进一步分析了储能设备自身的运行参数对风电系统可靠性影响。算例结果表明:在具有同样设备容量的情况下,3种储能策略对可靠性的改善不尽相同;在同一储能策略下,能量型电池储能设备对系统的可靠性改善更佳;同时,设备运行参数变化对系统可靠性指标也有一定的影响。
MENG Hongnian XIE Kaigui . Wind farm reliability evaluation considering operation characteristics of battery energy storage devices
[J]. Power System Technology , 2012 ,36 (6 ):214 -219 .
URL
[本文引用: 1]
在含电池储能设备风电场功率时序模型的基础上,建立了含功率型和能量型电池储能设备的风电场可靠性时序评估模型。使用RBTS发电系统作为算例,分析了2类电池设备在不同储能策略下对风电系统可靠性改善的程度,并进一步分析了储能设备自身的运行参数对风电系统可靠性影响。算例结果表明:在具有同样设备容量的情况下,3种储能策略对可靠性的改善不尽相同;在同一储能策略下,能量型电池储能设备对系统的可靠性改善更佳;同时,设备运行参数变化对系统可靠性指标也有一定的影响。
[18]
KONGNAM C NUCHPRAYOON S PREMRUDEEP REECHACHACHARN S , et al . Decision analysis on generation capacity of a wind park
[J]. Renewable and Sustainable Energy Reviews , 2009 ,13 (8 ):2126 -2133 .
DOI:10.1016/j.rser.2009.01.023
URL
[本文引用: 1]
[19]
ZHANG P WANG Y XIAO W , et al . Reliability evaluation of grid-connected photovoltaic power systems
[J]. IEEE Transactions on Sustainable Energy , 2012 ,3 (3 ):379 -389 .
DOI:10.1109/TSTE.2012.2186644
URL
[本文引用: 1]
This study presents a systematic way to evaluate reliability performance of large grid-connected photovoltaic (PV) power systems considering variation of input power and ambient-condition-dependent failure rates of critical components including PV modules, inverters, and capacitors. State enumeration is used to analyze real-life grid-connected PV systems. Ambient-condition-dependent failure rates of major components in PV systems are formulated and incorporated in reliability analysis. A series of reliability indices are defined to quantify PV systems' reliability performance. In addition, sensitivity analyses are extensively conducted to investigate the impact of different factors on the performances of PV power systems. Test results on a practical 20-kW PV project are presented to demonstrate the effectiveness of the proposed method.
[20]
杨锡运 , 刘玉奇 , 张璜 , 等 . 含并网光伏电站的系统可靠性评估方法
[J]. 高电压技术 , 2016 ,42 (9 ):2689 -2696 .
[本文引用: 1]
YANG Xiyun LIU Yuqi ZHANG Huang , et al . Reliability evaluation method of grid connected with photovoltaic power station
[J]. High Voltage Engineering , 2016 ,42 (9 ):2689 -2696 .
[本文引用: 1]
[21]
应飞祥 , 何民 , 姜燕波 , 等 . 光伏发电及其所处电力系统可靠性评估研究进展
[J]. 云南民族大学学报 , 2019 ,28 (5 ):523 -530 .
[本文引用: 1]
YING Feixiang HE Min JIANG Yanbo , et al . Research progress on photovoltaic power generation and reliability assessment of its power system
[J]. Journal of Yunnan Minzu University , 2019 ,28 (5 ):523 -530 .
[本文引用: 1]
[22]
方鑫 , 郭强 , 张东霞 , 等 . 考虑天气不确定性的光伏电站置信容量评估
[J]. 电力系统自动化 , 2012 ,36 (10 ):27 -32 .
URL
[本文引用: 1]
光伏发电由于具有间歇性和波动性,一般认为只有能量价值而没有容量价值,但在光伏电站并网后电力系统的发电可靠性会有所提升,这表明光伏发电也具有一定的容量价值,如何衡量其置信容量是大规模光伏电站接入电网时需要考虑的问题之一。文中提出了一种评估光伏电站置信容量的计算方法。首先,根据1年中天气情况建立考虑不同天气概率、最大辐射强度、云遮蔽以及温度波动的年光伏电站输出功率波动模型;其次,采用了基于序贯蒙特卡洛仿真的电力系统发电可靠性计算方法,在此基础上应用弦截法进行光伏电站置信容量的迭代求解,并将数理统计中的检验2个大子样均值相等——u检验的假设检验方法引入到迭代求解的收敛性判据之中;最后,应用可靠性标准算例的仿真计算,证明了所述方法的正确性和有效性。
FANG Xin GUO Qiang ZHANG Dongxia , et al . Capacity credit evaluation of grid-connected photovoltaic genera- tion considering weather uncertainty
[J]. Automation of Electric Power Systems , 2012 ,36 (10 ):27 -32 .
URL
[本文引用: 1]
光伏发电由于具有间歇性和波动性,一般认为只有能量价值而没有容量价值,但在光伏电站并网后电力系统的发电可靠性会有所提升,这表明光伏发电也具有一定的容量价值,如何衡量其置信容量是大规模光伏电站接入电网时需要考虑的问题之一。文中提出了一种评估光伏电站置信容量的计算方法。首先,根据1年中天气情况建立考虑不同天气概率、最大辐射强度、云遮蔽以及温度波动的年光伏电站输出功率波动模型;其次,采用了基于序贯蒙特卡洛仿真的电力系统发电可靠性计算方法,在此基础上应用弦截法进行光伏电站置信容量的迭代求解,并将数理统计中的检验2个大子样均值相等——u检验的假设检验方法引入到迭代求解的收敛性判据之中;最后,应用可靠性标准算例的仿真计算,证明了所述方法的正确性和有效性。
[23]
葛少云 , 王浩鸣 , 王源山 , 等 . 含分布式风光蓄的配电系统可靠性评估
[J]. 电力系统自动化 , 2012 ,36 (5 ):16 -23 .
URL
[本文引用: 1]
储能可以平滑分布式电源出力的波动性,挖掘其提升配电系统供电可靠性的潜力。为了定量评估储能装置的这种效果,提出了一种含分布式风机、光伏阵列和蓄电池的配电系统准序贯蒙特卡洛可靠性评估方法。在建立了风光蓄元件的时序模型和状态转移模型的基础上,对系统中的非电源元件进行序贯抽样,而对风光蓄元件进行非序贯抽样。讨论了含风光蓄配电系统的故障效果影响分析过程,给出了相应的可靠性评估流程。以改造的IEEE RBTS系统为例,对不同情境下的系统可靠性水平进行了对比分析,验证了所述方法的有效性。
GE Shaoyun WANG Haoming WANG Yuanshan , et al . Reliability evaluation of distribution system including distributed wind turbines,photovoltaic arrays and batteries
[J]. Automation of Electric Power Systems , 2012 ,36 (5 ):16 -23 .
URL
[本文引用: 1]
储能可以平滑分布式电源出力的波动性,挖掘其提升配电系统供电可靠性的潜力。为了定量评估储能装置的这种效果,提出了一种含分布式风机、光伏阵列和蓄电池的配电系统准序贯蒙特卡洛可靠性评估方法。在建立了风光蓄元件的时序模型和状态转移模型的基础上,对系统中的非电源元件进行序贯抽样,而对风光蓄元件进行非序贯抽样。讨论了含风光蓄配电系统的故障效果影响分析过程,给出了相应的可靠性评估流程。以改造的IEEE RBTS系统为例,对不同情境下的系统可靠性水平进行了对比分析,验证了所述方法的有效性。
[24]
孟虹年 . 计及电池储能设备运行特性的风电场可靠性评估
[D]. 重庆:重庆大学 , 2012 .
[本文引用: 2]
MENG Hongnian . Reliability assessment of wind frarms with operating characteristics of battery energy storage equipment
[D]. Chongqing:Chongqing University , 2012 .
[本文引用: 2]
[25]
王凯 , 栗文义 , 李龙 , 等 . 含风/光互补发电系统可靠性与经济性评估
[J]. 电工电能新技术 , 2015 ,34 (6 ):52 -56 .
[本文引用: 2]
WANG Kai LI Wenyi LI Long , et al . Reliability and economy evaluation of complementary power systems containing wind and solar energy
[J]. Advanced Technology of Electrical Engineering & Energy , 2015 ,34 (6 ):52 -56 .
[本文引用: 2]
[26]
刘峪涵 , 汪沨 , 谭阳红 . 并网型微电网多目标容量优化配置及减排效益分析
[J]. 电力系统及其自动化学报 , 2017 ,29 (9 ):70 -75 .
[本文引用: 1]
LIU Yuhan WANG Feng TAN Yanghong . Multi-objective optimal capacity configuration and emission reduction benefit analysis of grid-connected microgrid
[J]. Proceedings of the CSU-EPSA , 2017 ,29 (9 ):70 -75 .
[本文引用: 1]
集中式与集散式光伏发电系统MPPT的仿真与对比
1
2018
... 随着能源需求的不断增长,化石能源的日益消耗,以风能、太阳能为主的可再生能源在发电系统中得到了较为广泛的应用,但风光发电易受周围环境因素的影响,具有波动性和可间断性的特点[1 -3 ] .此外,风光发电的成本与收益问题也极大影响其在电力系统中的应用.因此,对含风光机组小型发电系统的可靠性与经济性评估研究具有重要意义. ...
集中式与集散式光伏发电系统MPPT的仿真与对比
1
2018
... 随着能源需求的不断增长,化石能源的日益消耗,以风能、太阳能为主的可再生能源在发电系统中得到了较为广泛的应用,但风光发电易受周围环境因素的影响,具有波动性和可间断性的特点[1 -3 ] .此外,风光发电的成本与收益问题也极大影响其在电力系统中的应用.因此,对含风光机组小型发电系统的可靠性与经济性评估研究具有重要意义. ...
基于序贯蒙特卡洛模拟的风光储发电系统可靠性评估
0
2017
基于序贯蒙特卡洛模拟的风光储发电系统可靠性评估
0
2017
基于风光互补出力特性的可消纳容量研究
1
2019
... 随着能源需求的不断增长,化石能源的日益消耗,以风能、太阳能为主的可再生能源在发电系统中得到了较为广泛的应用,但风光发电易受周围环境因素的影响,具有波动性和可间断性的特点[1 -3 ] .此外,风光发电的成本与收益问题也极大影响其在电力系统中的应用.因此,对含风光机组小型发电系统的可靠性与经济性评估研究具有重要意义. ...
基于风光互补出力特性的可消纳容量研究
1
2019
... 随着能源需求的不断增长,化石能源的日益消耗,以风能、太阳能为主的可再生能源在发电系统中得到了较为广泛的应用,但风光发电易受周围环境因素的影响,具有波动性和可间断性的特点[1 -3 ] .此外,风光发电的成本与收益问题也极大影响其在电力系统中的应用.因此,对含风光机组小型发电系统的可靠性与经济性评估研究具有重要意义. ...
Effects of wind power on bulk system adequacy evaluation using the well-being analysis framework
2
2009
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
... .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于 Well-Being 模型的风力发电系统可靠性评估
1
2011
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于 Well-Being 模型的风力发电系统可靠性评估
1
2011
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于模糊聚类的含风电场发电系统可靠性分析
1
2016
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于模糊聚类的含风电场发电系统可靠性分析
1
2016
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
含光伏电站的发电系统可靠性分析
1
2013
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
含光伏电站的发电系统可靠性分析
1
2013
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于Copula理论的风光互补发电系统可靠性评估
1
2013
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
基于Copula理论的风光互补发电系统可靠性评估
1
2013
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
含风光互补的独立发电系统可靠性评估
3
2019
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
... 本文中风力发电机切入风速为20 km/h、额定风速为41 km/h、切出风速为66 km/h、额定功率为1 kW[9 ] ,采用自回归滑动模型模拟出的一年逐时风速数据,如图5 所示.风机的三状态转移率分别取λ 1 =7.96次/年、λ 2 =5.84次/年、μ 1 =58.4次/年、μ 2 =48.3次/年,假设风机降额功率为正常输出功率的0.8倍. ...
... 光伏发电机组的额定功率${{p}_{sn}}$取1 kW,额定光强${{G}_{std}}$取1 kW/m2 ,某一特定光强${{R}_{c}}$取0.15 kW/m2 ,光伏发电机组的双状态转移率${{\lambda }_{3}}{{\mu }_{3}}$分别取 10.84次/年、48.3次/年,光辐照度数据如图 6 所示[9 ] . ...
含风光互补的独立发电系统可靠性评估
3
2019
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
... 本文中风力发电机切入风速为20 km/h、额定风速为41 km/h、切出风速为66 km/h、额定功率为1 kW[9 ] ,采用自回归滑动模型模拟出的一年逐时风速数据,如图5 所示.风机的三状态转移率分别取λ 1 =7.96次/年、λ 2 =5.84次/年、μ 1 =58.4次/年、μ 2 =48.3次/年,假设风机降额功率为正常输出功率的0.8倍. ...
... 光伏发电机组的额定功率${{p}_{sn}}$取1 kW,额定光强${{G}_{std}}$取1 kW/m2 ,某一特定光强${{R}_{c}}$取0.15 kW/m2 ,光伏发电机组的双状态转移率${{\lambda }_{3}}{{\mu }_{3}}$分别取 10.84次/年、48.3次/年,光辐照度数据如图 6 所示[9 ] . ...
Reliability cost/worth associated with wind energy and energy storage utilization in electric power systems
2
2008
... 目前,国内外学者对含风光机组的可靠性评估进行了一定的研究[4 -10 ] .文献[4 ]通过自回归滑动模型获得预测风速,基于预测风速得到风电场实时出力,并结合常规发电机组容量曲线及负荷需求曲线,采用序贯蒙特卡洛法对含风电场的发电系统进行可靠性评估.文献[5 ]基于蒙特卡洛法对风力发电系统进行可靠性评估,研究储能容量和峰值负荷这两种因素对小型孤立风力发电系统可靠性的具体影响.文献[6 ]根据实测数据对多个状态的风电场各状态间的转移概率进行计算,并采用序贯蒙特卡洛法评估了含风电场的发电系统可靠性.文献[7 ]考虑了不同状态下的晴空指数及辐照度波动指标对含光伏电场的发电系统可靠性的影响,分时模拟了给定状态下的辐照度,并基于RBTS测试系统采用序贯蒙特卡洛法对系统的可靠性进行了评估.文献[8 ]在考虑风光出力随机性及相关性的前提下,对风光互补发电系统可靠性进行评估.文献[9 ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
... ]在考虑了风光发电机组降额、停运等因素影响的基础上,基于序贯蒙特卡洛法评估了含风光互补的独立发电系统可靠性.上述文献都只评估了含新能源的发电系统的可靠性,均未计及新能源发电对系统可靠性及经济性的综合影响.文献[10 ]则评估了风柴储发电系统的可靠性与经济性,但却未涉及光伏发电. ...
1
2015
... 在发电系统可靠性评估中可分为孤立系统和互联系统两大类,本文考虑包括传统发电、风力发电和太阳能发电的孤立发电系统,含风光发电的孤立发电系统如图1 所示.当系统发电功率大于等于系统总负荷时为可靠状态,否则为不可靠状态[11 -12 ] .由于本文中系统发电功率包括风/光互补发电系统及常规机组的出力,因此在风光发电系统可靠性评估模型中需要建立风电机组及光伏机组出力模型. ...
1
2015
... 在发电系统可靠性评估中可分为孤立系统和互联系统两大类,本文考虑包括传统发电、风力发电和太阳能发电的孤立发电系统,含风光发电的孤立发电系统如图1 所示.当系统发电功率大于等于系统总负荷时为可靠状态,否则为不可靠状态[11 -12 ] .由于本文中系统发电功率包括风/光互补发电系统及常规机组的出力,因此在风光发电系统可靠性评估模型中需要建立风电机组及光伏机组出力模型. ...
风力发电为主导的孤立发电系统可靠性评估
1
2011
... 在发电系统可靠性评估中可分为孤立系统和互联系统两大类,本文考虑包括传统发电、风力发电和太阳能发电的孤立发电系统,含风光发电的孤立发电系统如图1 所示.当系统发电功率大于等于系统总负荷时为可靠状态,否则为不可靠状态[11 -12 ] .由于本文中系统发电功率包括风/光互补发电系统及常规机组的出力,因此在风光发电系统可靠性评估模型中需要建立风电机组及光伏机组出力模型. ...
风力发电为主导的孤立发电系统可靠性评估
1
2011
... 在发电系统可靠性评估中可分为孤立系统和互联系统两大类,本文考虑包括传统发电、风力发电和太阳能发电的孤立发电系统,含风光发电的孤立发电系统如图1 所示.当系统发电功率大于等于系统总负荷时为可靠状态,否则为不可靠状态[11 -12 ] .由于本文中系统发电功率包括风/光互补发电系统及常规机组的出力,因此在风光发电系统可靠性评估模型中需要建立风电机组及光伏机组出力模型. ...
Reliability evaluation considering wind and hydro power coordination
1
2010
... 基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] .通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化.风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] . ...
含风储系统的电力系统可靠性评估进展与展望
1
2019
... 基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] .通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化.风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] . ...
含风储系统的电力系统可靠性评估进展与展望
1
2019
... 基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] .通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化.风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] . ...
含风电接入的发输电系统风险评估
1
2014
... 基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] .通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化.风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] . ...
含风电接入的发输电系统风险评估
1
2014
... 基于历史实测风速,采用自回归滑动模型进行风速预测[13 ] .通常情况下由于风机降额运行时间短,一般只计及正常与停运两种状态,但为了使可靠性评估结果更精确,本文考虑了风机的降额状态,但在实际运行过程中由于降额与停运间的转换产生概率较小[14 ] ,因此本文不计两者间的互相转化.风力发电机组可靠性模型的三状态空间模型如图2 所示[15 ] . ...
风电场及储能装置对发输电系统可靠性的影响
1
2011
... 基于预测风速${{v}_{t}}$,采用分段函数表示风电机组输出功率[16 -17 ] ,并在考虑风机三状态空间模型的情况下得到最终风电机组输出功率. ...
风电场及储能装置对发输电系统可靠性的影响
1
2011
... 基于预测风速${{v}_{t}}$,采用分段函数表示风电机组输出功率[16 -17 ] ,并在考虑风机三状态空间模型的情况下得到最终风电机组输出功率. ...
计及电池储能设备运行特性的风电场可靠性评估
1
2012
... 基于预测风速${{v}_{t}}$,采用分段函数表示风电机组输出功率[16 -17 ] ,并在考虑风机三状态空间模型的情况下得到最终风电机组输出功率. ...
计及电池储能设备运行特性的风电场可靠性评估
1
2012
... 基于预测风速${{v}_{t}}$,采用分段函数表示风电机组输出功率[16 -17 ] ,并在考虑风机三状态空间模型的情况下得到最终风电机组输出功率. ...
Decision analysis on generation capacity of a wind park
1
2009
... 式中,${{p}_{ti}}$为每台风机$t$时刻的实时出力;${{p}_{r}}$为风机额定功率;${{v}_{ci}}{{v}_{r}}{{v}_{co}}$分别为风机的切入风速、额定风速及切出风速;$\alpha \beta \gamma $分别为风电机组功率特性曲线的待定系数[18 ] . ...
Reliability evaluation of grid-connected photovoltaic power systems
1
2012
... 光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] .因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示. ...
含并网光伏电站的系统可靠性评估方法
1
2016
... 光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] .因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示. ...
含并网光伏电站的系统可靠性评估方法
1
2016
... 光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] .因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示. ...
光伏发电及其所处电力系统可靠性评估研究进展
1
2019
... 光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] .因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示. ...
光伏发电及其所处电力系统可靠性评估研究进展
1
2019
... 光伏发电系统的组成较风机而言较为复杂,其中的任意元件故障都有可能对光伏出力产生直接的影响,造成机组停运[19 ] .因此,本文的光伏发电机组可靠性模型不考虑降额状态,直接采用双状态模型[20 -21 ] ,如图3 所示. ...
考虑天气不确定性的光伏电站置信容量评估
1
2012
... 图3 中,${{\lambda }_{3}}$为光伏发电机组停运状态的转移率;${{\mu }_{3}}$为修复率;运行持续时间${{\tau }_{3}}$及停运故障修复时间${{\tau }_{4}}$分别如式(6)、(7)[22 ] 所示. ...
考虑天气不确定性的光伏电站置信容量评估
1
2012
... 图3 中,${{\lambda }_{3}}$为光伏发电机组停运状态的转移率;${{\mu }_{3}}$为修复率;运行持续时间${{\tau }_{3}}$及停运故障修复时间${{\tau }_{4}}$分别如式(6)、(7)[22 ] 所示. ...
含分布式风光蓄的配电系统可靠性评估
1
2012
... 基于由Homer软件生成的光辐照度实时序列,采用分段函数表示光伏发电机组的输出功率[23 ] ,并在考虑光伏双状态空间模型的情况下得到最终光伏发电机组输出功率. ...
含分布式风光蓄的配电系统可靠性评估
1
2012
... 基于由Homer软件生成的光辐照度实时序列,采用分段函数表示光伏发电机组的输出功率[23 ] ,并在考虑光伏双状态空间模型的情况下得到最终光伏发电机组输出功率. ...
计及电池储能设备运行特性的风电场可靠性评估
2
2012
... (4) 可靠性成本函数,即在可靠性评估过程中因负荷缺电量造成的成本费用[24 ] 的函数表达式为 ...
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...
计及电池储能设备运行特性的风电场可靠性评估
2
2012
... (4) 可靠性成本函数,即在可靠性评估过程中因负荷缺电量造成的成本费用[24 ] 的函数表达式为 ...
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...
含风/光互补发电系统可靠性与经济性评估
2
2015
... 节约燃料带来的收益模型采用如下所示[25 ] ...
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...
含风/光互补发电系统可靠性与经济性评估
2
2015
... 节约燃料带来的收益模型采用如下所示[25 ] ...
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...
并网型微电网多目标容量优化配置及减排效益分析
1
2017
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...
并网型微电网多目标容量优化配置及减排效益分析
1
2017
... 风力发电机组的单位千瓦时投资为4 620 元/ kW·h,每台风力发电机组的单位运行与维护成本为32.9 元/kW·h;光伏发电机组的单位千瓦时投资为6 350 元/kW·h,每台光伏发电机组的单位运行与维护成本为16.1 元/kW·h.假设风力发电与光伏发电机组的折旧年限与贴现率均分别取20年和6%;常规发电机组的燃料成本系数a 、b 、c 分别取为0.004 3、21.6、958.2,常规发电机组的单位千瓦时投资为1 866 元/kW·h,运行维护成本为10.5 元/kW·h;可靠性成本中加权平均系数分别取0.36和0.64,产电比为6.652 元/kW·h,电价倍数为25,平均电价为0.45 元/kW·h;热耗率为3.2 kW·h/L,燃料价格为7.28 元/L[24 -25 ] ;常规机组生产单位电能产生的有害气体排放量及处理费用如表1 [26 ] 所示. ...