1 引言
近年来,由于温室气体增加导致的气候变化加剧了极端灾害(如台风、洪水和冰灾等)出现的频率和破坏性,引发了电力系统出现多次大规模故障,造成了巨大的经济损失和不良的社会影响。因此,有学者提出了韧性的概念以衡量电力系统抵御极端灾害的能力。配电网韧性可定义为配电网对小概率-大影响扰动的抵御、适应和快速恢复的能力[1 ] ,提高韧性有利于缩小配电网在极端灾害下的停电范围,减少负荷损失[2 ] 。
目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] 。通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] 。以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] 。
传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] 。这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解。后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担。因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] 。文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响。但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性。文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性。
针对上述问题,本文综合考虑分布式电源和可控负荷的作用,建立了面向韧性提升的配电网开关优化配置模型。首先,梳理了韧性、可靠性和自愈能力之间的关系,描述了配电网韧性的分析过程与量化方法;其次,考虑分布式电源和可控负荷的作用,以混合整数线性规划模型的形式建立了适用于多重故障场景的配电网开关优化配置模型,将配电网韧性最大化,并提出了开关优化配置的整体流程;最后,通过算例分析验证了所提模型的有效性与合理性。
2 配电网韧性概念
2.1 韧性、可靠性和自愈能力的关系
韧性、可靠性和自愈能力是从不同侧面反映配电网应对故障的能力。韧性指配电网在极端灾害下的供电恢复能力,重点关注在小概率-大影响故障下配电网对关键负荷的支撑能力;可靠性指长时间尺度下配电网对用户持续供电的能力,重点关注大概率-小影响的单重故障;自愈能力则是指利用先进的配电自动化技术,在故障发生前自我预防,在故障发生后快速隔离故障,实现自我恢复。本文将韧性、可靠性和自愈能力三个概念之间的关系进行梳理,具体关系如表1 所示。
2.2 配电网韧性分析方法与量化过程
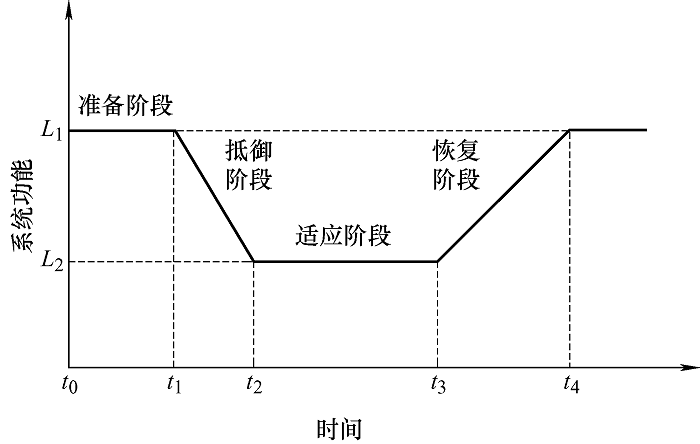
根据图1 中极端灾害下配电网系统功能曲线,可以将韧性分析过程划分为如下四个阶段:准备阶段(t 0 -t 1 )、抵御阶段(t 1 -t 2 )、适应阶段(t 2 -t 3 )和恢复阶段(t 3 -t 4 )。
图1
t 1 时刻之前,系统保持正常运行,处于准备阶段;系统在t 1 时刻发生故障,从t 1 至t 2 时段的事故进程中系统功能水平由L 1 降为L 2 ,处于抵御阶段;t 2 时刻,系统运行人员通过网络重构、调度分布式电源出力和需求侧管理等主动措施进行响应,最大程度地提高功能水平;t 3 时刻,系统分配抢修资源,执行故障恢复计划,负荷逐渐并网恢复供电,t 4 时刻达到正常状态。
对配电网韧性量化分析需要选择合适的指标,本文将极端灾害期间系统功能维持正常状态的比例作为韧性指标[3 ] ,如式(1)所示
(1) $\alpha =\frac{\int_{\ {{t}_{1}}}^{\ {{t}_{4}}}{{{L}_{\text{R}}}(t)\text{d}t}}{\int_{\ {{t}_{1}}}^{\ {{t}_{4}}}{{{L}_{\text{T}}}(t)\text{d}t}}=\frac{\int_{\ {{t}_{1}}}^{\ {{t}_{4}}}{\sum\limits_{i=1}^{N}{{{\omega }_{i}}{{c}_{i,t}}P{{L}_{i,t}}}\text{d}t}}{\int_{\ {{t}_{1}}}^{\ {{t}_{4}}}{\sum\limits_{i=1}^{N}{{{\omega }_{i}}P{{L}_{i,t}}}\text{d}t}}$
式中,α 为配电网韧性指标;L R (t )为t 时刻系统实际功能;L T (t )为t 时刻系统正常功能。本文采用加权负荷曲线描述系统功能,N 为配电网负荷节点个数;ωi 为节点i 处负荷的权重系数;PLi,t 为t 时刻节点i 的负荷大小;ci , t t 时刻节点i 处负荷是否维持供电,维持为1,反之为0。
3 配电网开关优化配置模型
3.1 停电负荷量计算模型
当辐射状配电网发生单重或多重故障时,根据开关与故障区域的相对位置,受影响的负荷可以分为三类。第一类是位于源节点和第一故障区域之间的负荷,这些负荷可以通过改变开关状态与故障区域隔离,继续由上级电网供电。第二类是位于配电网故障区域内的负荷,无法通过开关与隔离故障,只能等故障修复后才能恢复供电。第三类是位于故障区域下游孤岛区的负荷。若该区域内有足够的可用容量,则孤岛内所有负荷均恢复供电,否则应根据负荷的重要程度或可控性断开部分负荷,以维持发电量和用电需求间的平衡。本文中,考虑两种负荷削减方式,第一种是负荷点处配有负荷开关,利用负荷开关控制负荷供电情况;第二种是考虑部分负荷具有可控性,允许进行一定比例的削减。下面分别以单重故障和双重故障为例介绍配电网停电负荷量的计算模型。
(2) $y_{k,j,f}^{\text{U}}\ge 1-\sum\limits_{s=2k}^{2j-2}{{{x}_{s,f}}}$
(3) $y_{k,j,f}^{\text{D}}\ge 1-\sum\limits_{s=2j-\text{1}}^{2k-1}{{{x}_{s,f}}}$
式中,$y_{k,j,f}^{\text{U}}$和$y_{k,j,f}^{\text{D}}$为二元变量,为0表示在馈线f 中分段j 故障时,负荷点k 属于第一类负荷或第三类负荷,为1表示负荷点k 属于第二类负荷;Xs , f f 中位置s 处安装开关,为0表示不安装,本文设置开关候选安装位置为馈线分段的首末两端。式(2)、(3)表示若负荷点与故障间安装开关,则可与故障区进行隔离,通过上级电源或分布式电源供电,否则该负荷点属于第二类负荷,故障修复后方可恢复供电。
(4) $\begin{align} p_{k,j,f,t}^{\text{Gen}}-\beta _{k,j,f,t}^{\text{D}}{{p}_{k,t}}=\sum\limits_{m=1.m\ne k}^{{{N}_{\text{LP}}}}{(}\frac{{{x}_{k,m}}}{r_{k,m}^{2}+x_{k,m}^{2}}\times \begin{matrix} {} {} \\ \end{matrix}\Delta {{\theta }_{k,m,j,f,t}}+\frac{{{r}_{k,m}}}{r_{k,m}^{2}+x_{k,m}^{2}}\Delta {{v}_{k,m,j,f,t}}) \\ \end{align}$
(5) $\begin{align} q_{k,j,f,t}^{\text{Gen}}-\beta _{k,j,f,t}^{\text{D}}{{q}_{k,t}}=\sum\limits_{m=1.m\ne k}^{{{N}_{\text{LP}}}}{(}\frac{-{{r}_{k,m}}}{r_{k,m}^{2}+x_{k,m}^{2}}\times \begin{matrix} {} {} \\ \end{matrix}\Delta {{\theta }_{k,m,j,f,t}}+\frac{{{x}_{k,m}}}{r_{k,m}^{2}+x_{k,m}^{2}}\Delta {{v}_{k,m,j,f,t}}) \\ \end{align}$
式中,$p_{k,j,f,t}^{\text{Gen}}$和$q_{k,j,f,t}^{\text{Gen}}$分别为t 时刻节点k 处分布式电源有功出力和无功出力大小;pk , t qk , t t 时刻节点k 处负荷大小;$\beta _{k,j,f,t}^{\text{D}}$为负荷削减比例;N LP 为负荷点个数;rk , m xk , m
(6) $\sum\limits_{k=1}^{{{N}_{\text{LP}}}}{p_{k,j,f,t}^{\text{Gen}}}\ge \sum\limits_{k=1}^{{{N}_{\text{LP}}}}{\beta _{k,j,f,t}^{\text{D}}{{p}_{k,t}}}$
(7) $\sum\limits_{k=1}^{{{N}_{\text{LP}}}}{q_{k,j,f,t}^{\text{Gen}}}\ge \sum\limits_{k=1}^{{{N}_{\text{LP}}}}{\beta _{k,j,f,t}^{\text{D}}{{q}_{k,t}}}$
(8) $p_{k,j,f,t}^{\text{Gen}}\le (1-y_{k,j,f}^{\text{D}})p_{k}^{\max }$
(9) $q_{k,j,f,t}^{\text{Gen}}\le (1-y_{k,j,f}^{\text{D}})q_{k}^{\max }$
式中,$p_{k}^{\max }$和$q_{k}^{\max }$分别为节点k 处分布式电源有功出力和无功出力上限。
(10) $\beta _{k,j,f,t}^{\text{D}}\le 1-y_{k,j,f}^{\text{D}}$
(11) $\beta _{k,j,f,t}^{\text{D}}\le {{u}_{k,j,f,t}}$
(12) $\beta _{k,j,f,t}^{\text{D}}\ge (1-{{r}_{k}})({{u}_{k,j,f,t}}-y_{k,j,f}^{\text{D}})$
式中,uk,j,f,t 为二元变量,表示节点k 的故障状态,1表示未故障,0表示故障;rk 为负荷最大允许削减比例。
(13) $y_{k,j,l,f}^{\text{U}}\ge 1-\sum\limits_{s=2k}^{2j-2}{{{x}_{s,f}}}$
(14) $y_{k,j,l,f}^{\text{D,B}}\ge 1-\sum\limits_{s=2j-1}^{2k-1}{{{x}_{s,f}}}$
(15) $y_{k,j,l,f}^{\text{U,B}}\ge 1-\sum\limits_{s=2k}^{2l-2}{{{x}_{s,f}}}$
(16) $y_{k,j,l,f}^{\text{B}}\ge y_{k,j,l,f}^{\text{D,B}}$
(17) $y_{k,j,l,f}^{\text{B}}\ge y_{k,j,l,f}^{\text{U,B}}$
(18) $y_{k,j,l,f}^{\text{B}}\ge y_{k,j,l,f}^{\text{U,B}}\text{+}y_{k,j,l,f}^{\text{D,B}}$
式中,$y_{k,j,l,f}^{\text{U}}$为二元变量,表示当在馈线f 中分段j 和l 故障时,第一处故障(分段j )上游负荷点负荷类型,1为第二类负荷,0为第一类负荷;$y_{k,j,l,f}^{\text{D,B}}$和$y_{k,j,l,f}^{\text{U,B}}$为二元辅助变量;$y_{k,j,l,f}^{\text{B}}$为二元变量,表示位于两处故障中间负荷点的负荷类型,1为第二类负荷,0为第三类负荷。式(16)~(18)表示只有当负荷点与两处故障间均安装有开关时,该负荷点才属于第三类负荷,否则属于第二类负荷。同时,双重故障中第三类负荷所处的孤岛区也要满足单重故障中式(2)~(12)表示的各项约束。值得一提的是,本文虽然只详细描述了单重故障和双重故障下停电负荷量的计算模型,但是能够很容易从中提取出多重故障下停电负荷量计算模型,不再赘述。
除式(2)~(18)外,配电网开关优化配置模型还需要满足预算约束
(19) $\sum\limits_{f=1}^{{{N}_{f}}}{\sum\limits_{s=1}^{{{N}_{f,\ s}}}{{{x}_{f,s}}}}\le {{N}_{S}}$
式中,Nf 为系统中馈线数量;Nf,s 为馈线f 中的分段数量;NS 为最多允许安装开关的个数。
3.2 目标函数
规划人员需要在配电网关键位置配置开关以保证配电系统的韧性水平,因此开关优化配置模型的目标函数为
(20) $\begin{align} & \ \ \underset{z\in Z}{\mathop{\max }}\,\alpha =1-(\sum\limits_{t=1}^{{{N}_{t}}}{\sum\limits_{f=1}^{{{N}_{f}}}{\sum\limits_{j=1}^{{{N}_{f,s}}}{\sum\limits_{k=1}^{{{N}_{LP}}}{{{\omega }_{k}}\times }}}} (y_{k,j,f}^{\text{D}}-\beta _{k,j,f,t}^{\text{D}}){{p}_{k,t}})/\sum\limits_{t=1}^{{{N}_{t}}}{\sum\limits_{k=1}^{{{N}_{LP}}}{{{\omega }_{k}}{{p}_{k,t}}}} \\ \end{align}$
式中,z 为配电网开关配置方案;Z 为配电网开关可行配置集;Nt 为配电网受极端灾害影响的时刻集合;ωk 为节点k 处负荷的权重系数。式(20)中减数的物理含义为极端灾害影响期间,配电网加权失负荷量。该目标函数的含义是在允许的开关配置方案下,尽可能提高配电网的韧性水平。
3.3 开关优化配置整体流程
(1) 输入配电网结构,模拟灾害场景,筛选出故障元件[3 ] 。
(2) 更新配电网结构,计算当前状态下的系统功能,生成最优故障抢修策略[19 ] 。
(3) 按照本文提出的开关优化配置模型,以最大化配电网韧性指标为目标,提升系统韧性。
(4) 如果配电网抢修结束,则按照式(20)计算配电网韧性,否则转至步骤(2)。
4 算例分析
4.1 算例概况
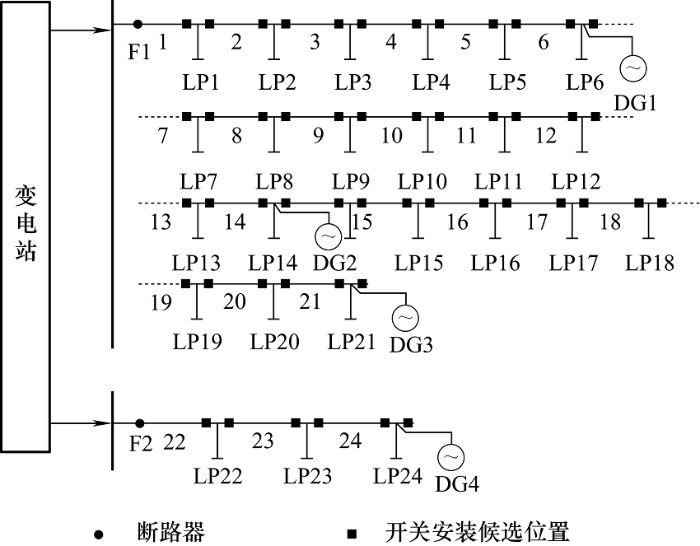
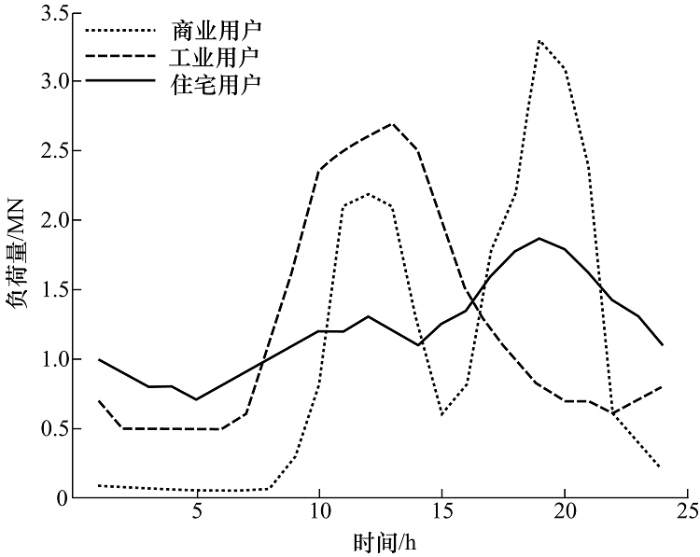
首先通过图2 中简单的测试算例对配电网开关优化配置问题进行说明,再通过典型的RBTS4算 例[20 ] 说明模型的有效性。本文侧重于对提升配电网韧性的开关优化配置模型研究,并未对灾害建模进行深入研究,因此选用文献[3 ]中的台风灾害模型和强度。测试算例中包含住宅、商业和工业三类负荷,加权因子分别为0.08、0.36和0.96,图3 为三类负荷的日负荷曲线。通过设置六种场景说明不同的运行策略对开关优化配置和配电网韧性的影响,如 表2 所示。在这六种场景中,考虑了不同分布式电源容量和采用不同负荷削减方式对韧性提升效果的影响。住宅、商业和工业用户的负荷最大允许削减比例分别为0.5、0.3和0。
图2
图3
4.2 算例结果与分析
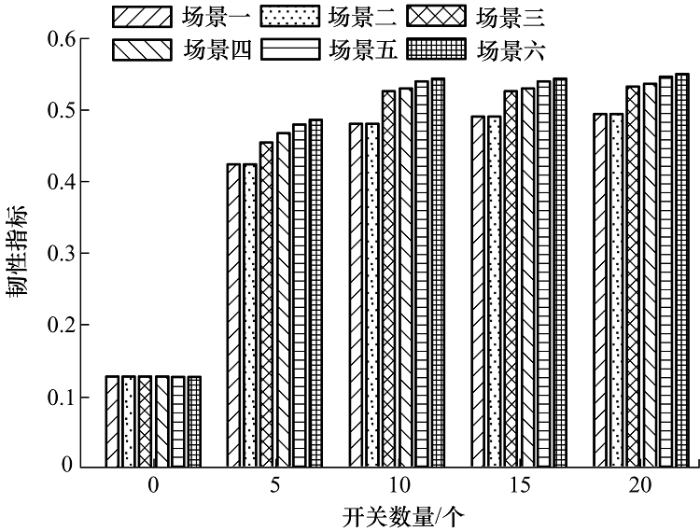
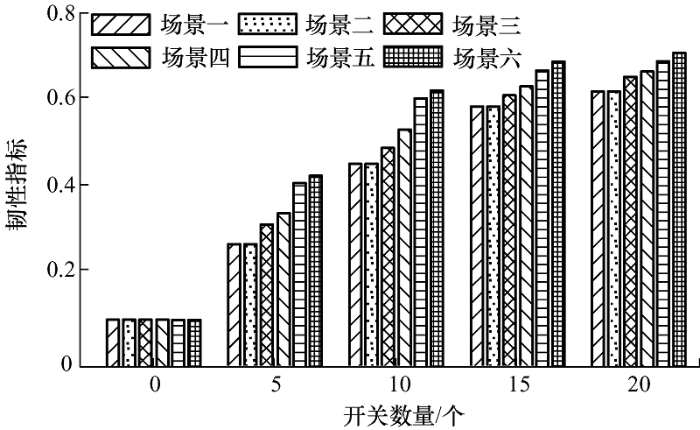
图4 为测试算例在不同场景下安装不同数量开关的韧性指标计算结果。如图4 所示,增加安装开关数量和增大分布式电源容量能够显著提高配电网韧性。与场景三和场景五相比,场景四和场景六由于更加多样化的负荷削减方式,其韧性提升效果更加明显。当最大允许安装开关数量为0时,灾害发生后负荷无法与故障区域隔离,因此测试算例内所有负荷均为第二类负荷,无论分布式电源容量是多少,其韧性指标均相同。另外,由于场景一和场景二中分布式电源容量不足,在灾害发生后无法为孤岛内的第三类负荷供电,因此韧性指标的大小与负荷削减方式无关。
图4
表3 、4 展示了场景六下最大允许安装开关数量分别为5和10时配电网开关的配置位置,其中B表示线路始端,E表示边路末端。由表3 、4 可知,开关的最优配置位置主要有三个类别:第一类是将开关配置在加权因子较高的负荷点附近,灾害后能够将负荷点与故障区域快速隔离,利用上级网络或本地分布式电源恢复供电。第二类是将开关配置在故障率较高的线路附近,灾害后能够通过最小化故障区域来最小化停电负荷量,进而提升配电网韧性。第三类是将开关配置在分布式电源的上游或下游,灾害发生后开关能够将分布式电源与故障区域快速隔离,以配电孤岛的形式恢复负荷供电。
在标准算例RTBS4系统上进行开关优化配置的仿真结果如图5 所示。与测试系统类似,在所有场景下增加最大允许安装开关数量和分布式电源容量都会提升配电网韧性。场景四和场景六中,多样化负荷削减方式也有利于提升韧性。场景一和场景二中由于分布式电源容量不足,因此具有相同的韧性指标,与负荷削减方式无关。
图5
5 结论
为加强配电网抵御极端自然灾害的能力,本文提出了一种面向韧性提升的配电网开关优化配置模型,得到如下结论。
(1) 在配电网关键位置配置开关能够在灾害发生后将负荷点和故障区域隔离,有利于恢复重要负荷供电,提高韧性,并且安装越多的开关对韧性的提升越明显。
(2) 分布式电源能够以配电孤岛的形式配合负荷削减的手段在灾害期间维持配电网重要负荷供电,提高分布式电源容量和多样化负荷削减方式能够有效提升配电网韧性。
本文仅从灾后恢复的角度研究了配电网开关优化配置问题,而配电网韧性提升方法还包含线路强化、网络重构等多种方式,同时目前电动汽车和储能技术也在快速发展,将这些新技术融入到韧性提升问题是未来的研究方向之一。
参考文献
View Option
[1]
别朝红 , 林雁翎 , 邱爱慈 . 弹性电网及其恢复力的基本概念与研究展望
[J]. 电力系统自动化 , 2015 ,39 (12 ):1 -9 .
[本文引用: 1]
BIE Zhaohong LIN Yanling QIU Aici . Concept and researchprospects of power system resilience
[J]. Automation of Electric Power Systems , 2015 ,39 (12 ):1 -9 .
[本文引用: 1]
[3]
周晓敏 , 葛少云 , 李腾 , 等 . 极端天气条件下的配电网韧性分析方法及提升措施研究
[J]. 中国电机工程学报 , 2018 ,38 (2 ):505 -513 .
[本文引用: 4]
ZHOU Xiaomin GE Shaoyun LI Teng , et al . Assessing and boosting resilience of distribution system under extreme weather
[J]. Proceedings of the CSEE , 2018 ,38 (2 ):505 -513 .
[本文引用: 4]
[4]
周生海 , 尹航 , 顾颖 , 等 . 基于POP NSGA-Ⅱ的配电网故障恢复重构
[J]. 电气工程学报 , 2018 ,13 (6 ):28 -35 .
[本文引用: 1]
ZHOU Shenghai YIN Hang GU Ying , et al . Service restoration reconfiguration in distribution systems based on pareto optimizing path NSGA-II
[J]. Journal of Electrical Engineering , 2018 ,13 (6 ):28 -35 .
[本文引用: 1]
[5]
WANG Y XU Y HE J , et al . Coordinating multiple sources for service restoration to enhance resilience of distribution systems
[J]. IEEE Transactions on Smart Grid , 2018 ,41 (3 ):256 -261 .
[本文引用: 1]
[6]
张安龙 , 翟学 , 李艳 , 等 . 含光伏电源的配电网故障定位策略研究
[J]. 电测与仪表 , 2015 ,52 (16 ):123 -128 .
[本文引用: 1]
ZHANG Anlong ZHAI Xue LI Yan , et al . Research on fault location strategy of distribution network with PV
[J]. Electric Measuring & Instrumentation , 2015 ,52 (16 ):123 -128 .
[本文引用: 1]
[7]
姜惠兰 , 钱广超 , 范中林 , 等 . 考虑负荷控制的有源配电网故障恢复策略
[J]. 中国电力 , 2017 ,50 (3 ):101 -106 .
[本文引用: 1]
JIANG Huilan QIAN Guangchao FAN Zhonglin , et al . A service restoration strategy considering influence of load management for distribution system with DG
[J]. Electric Power , 2017 ,50 (3 ):101 -106 .
[本文引用: 1]
[8]
LUTH J . Four rules to help locate protective devices
[J]. Electric World , 1991 ,205 (7 ):36 -37 .
[本文引用: 1]
[9]
于腾凯 , 李晓军 . 基于LCC和改进BDE法的配电网开关优化配置
[J]. 电测与仪表 , 2015 ,52 (13 ):96 -100 .
[本文引用: 1]
YU Tengkai LI Xiaojun . Optimal switching configuration of distribution network based on LCC and improved BDE
[J]. Electrical Measurement & Instrumentation , 2015 ,52 (13 ):96 -100 .
[本文引用: 1]
[10]
李子韵 , 成乐祥 , 王自桢 , 等 . 配电自动化终端布局规划方法
[J]. 电网技术 , 2016 ,40 (4 ):1271 -1276 .
DOI:10.13335/j.1000-3673.pst.2016.04.043
URL
[本文引用: 1]
In order to deal with problems of distribution terminal layout planning in distribution automation program, a layout planning method for distribution automation terminal is put forward. First, principle of distribution automation terminal configuration is analyzed, and method of distribution reliability evaluation considering distribution automation is studied. On these bases, optimization model with minimum total cost of primary switch equipments and distribution terminal investment, operation cost and loss of outrage as objective is established. Genetic algorithm is used to solve the model to determine place and type for distribution automation terminal. Finally, simulation result with IEEE RBTS BUS-2 shows that this method can get reasonable layout for distribution automation terminal.
LI Ziyun CHENG Lexiang WANG Zizhen , et al . A method of layout planning for distribution automation terminal
[J]. Power System Technology , 2016 ,40 (4 ):1271 -1276 .
DOI:10.13335/j.1000-3673.pst.2016.04.043
URL
[本文引用: 1]
In order to deal with problems of distribution terminal layout planning in distribution automation program, a layout planning method for distribution automation terminal is put forward. First, principle of distribution automation terminal configuration is analyzed, and method of distribution reliability evaluation considering distribution automation is studied. On these bases, optimization model with minimum total cost of primary switch equipments and distribution terminal investment, operation cost and loss of outrage as objective is established. Genetic algorithm is used to solve the model to determine place and type for distribution automation terminal. Finally, simulation result with IEEE RBTS BUS-2 shows that this method can get reasonable layout for distribution automation terminal.
[11]
BEZERRA J R BARROSO G C LEAO R P S , et al . Multi-objective optimization algorithm for switch placement in radial power distribution networks
[J]. IEEE Transactions on Power Delivery , 2015 ,30 (2 ):545 -552 .
DOI:10.1109/TPWRD.2014.2317173
URL
[本文引用: 1]
[12]
袁月 , 王守相 , 蒋菱 , 等 . 适应自愈要求的配电网开关优化配置
[J]. 中国电力 , 2016 ,49 (3 ):76 -82 .
[本文引用: 1]
YUAN Yue WANG Shouxiang JIANG Ling , et al . Switch configuration optimization based on self-healing requirement of distribution network
[J]. Electric Power , 2016 ,49 (3 ):76 -82 .
[本文引用: 1]
[14]
孙磊 , 杨贺钧 , 丁明 . 配电系统开关优化配置的混合整数线性规划模型
[J]. 电力系统自动化 , 2018 ,42 (16 ):87 -95 .
[本文引用: 2]
SUN Lei YANG Hejun DING Ming . Mixed integer linear programming model of optimal placement for switching devices in distribution system
[J]. Automation of Electric Power Systems , 2018 ,42 (16 ):87 -95 .
[本文引用: 2]
[15]
ABIRI-JAHROMI A FOTUHI-FIRUZABAD M PARVANIA M , et al . Optimized sectionalizing switch placement strategy in distribution systems
[J]. IEEE Transactions on Power Delivery , 2016 ,27 (1 ):362 -370 .
DOI:10.1109/TPWRD.2011.2171060
URL
[本文引用: 3]
[16]
SIIRTO O SAFDARIAN A LEHTONEN M , et al . Optimal distribution network automation considering earth fault events
[J]. IEEE Transactions on Smart Grid , 2018 ,6 (2 ):1010 -1018 .
DOI:10.1109/TSG.2014.2387471
URL
[本文引用: 2]
[18]
HEIDARI A AGELIDIS V KIA M . Considerations of sectionalizing switches in distribution networks with distributed generation
[J]. IEEE Transactions on Power Delivery , 2017 ,30 (3 ):1401 -1409 .
DOI:10.1109/TPWRD.2014.2385654
URL
[本文引用: 2]
[19]
赵丽敬 . 电网的弹性建模与评估
[D]. 武汉:华中科技大学 , 2015 .
[本文引用: 1]
ZHAO Lijing . Resilience modeling and evaluation of power grid
[D]. Wuhan:Huazhong University of Science and Technology , 2015 .
[本文引用: 1]
[20]
ALLAN R N BILLINTON R SJARIEF I , et al . A reliability test system for educational purposes-basic distribution system data and results
[J]. IEEE Transaction on Power System , 1991 ,6 (2 ):813 -820 .
DOI:10.1109/59.76730
URL
[本文引用: 1]
弹性电网及其恢复力的基本概念与研究展望
1
2015
... 近年来,由于温室气体增加导致的气候变化加剧了极端灾害(如台风、洪水和冰灾等)出现的频率和破坏性,引发了电力系统出现多次大规模故障,造成了巨大的经济损失和不良的社会影响.因此,有学者提出了韧性的概念以衡量电力系统抵御极端灾害的能力.配电网韧性可定义为配电网对小概率-大影响扰动的抵御、适应和快速恢复的能力[1 ] ,提高韧性有利于缩小配电网在极端灾害下的停电范围,减少负荷损失[2 ] . ...
弹性电网及其恢复力的基本概念与研究展望
1
2015
... 近年来,由于温室气体增加导致的气候变化加剧了极端灾害(如台风、洪水和冰灾等)出现的频率和破坏性,引发了电力系统出现多次大规模故障,造成了巨大的经济损失和不良的社会影响.因此,有学者提出了韧性的概念以衡量电力系统抵御极端灾害的能力.配电网韧性可定义为配电网对小概率-大影响扰动的抵御、适应和快速恢复的能力[1 ] ,提高韧性有利于缩小配电网在极端灾害下的停电范围,减少负荷损失[2 ] . ...
Battling the extreme:A study on the power system resilience
1
2017
... 近年来,由于温室气体增加导致的气候变化加剧了极端灾害(如台风、洪水和冰灾等)出现的频率和破坏性,引发了电力系统出现多次大规模故障,造成了巨大的经济损失和不良的社会影响.因此,有学者提出了韧性的概念以衡量电力系统抵御极端灾害的能力.配电网韧性可定义为配电网对小概率-大影响扰动的抵御、适应和快速恢复的能力[1 ] ,提高韧性有利于缩小配电网在极端灾害下的停电范围,减少负荷损失[2 ] . ...
极端天气条件下的配电网韧性分析方法及提升措施研究
4
2018
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
... 对配电网韧性量化分析需要选择合适的指标,本文将极端灾害期间系统功能维持正常状态的比例作为韧性指标[3 ] ,如式(1)所示 ...
... (1) 输入配电网结构,模拟灾害场景,筛选出故障元件[3 ] . ...
... 首先通过图2 中简单的测试算例对配电网开关优化配置问题进行说明,再通过典型的RBTS4算 例[20 ] 说明模型的有效性.本文侧重于对提升配电网韧性的开关优化配置模型研究,并未对灾害建模进行深入研究,因此选用文献[3 ]中的台风灾害模型和强度.测试算例中包含住宅、商业和工业三类负荷,加权因子分别为0.08、0.36和0.96,图3 为三类负荷的日负荷曲线.通过设置六种场景说明不同的运行策略对开关优化配置和配电网韧性的影响,如 表2 所示.在这六种场景中,考虑了不同分布式电源容量和采用不同负荷削减方式对韧性提升效果的影响.住宅、商业和工业用户的负荷最大允许削减比例分别为0.5、0.3和0. ...
极端天气条件下的配电网韧性分析方法及提升措施研究
4
2018
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
... 对配电网韧性量化分析需要选择合适的指标,本文将极端灾害期间系统功能维持正常状态的比例作为韧性指标[3 ] ,如式(1)所示 ...
... (1) 输入配电网结构,模拟灾害场景,筛选出故障元件[3 ] . ...
... 首先通过图2 中简单的测试算例对配电网开关优化配置问题进行说明,再通过典型的RBTS4算 例[20 ] 说明模型的有效性.本文侧重于对提升配电网韧性的开关优化配置模型研究,并未对灾害建模进行深入研究,因此选用文献[3 ]中的台风灾害模型和强度.测试算例中包含住宅、商业和工业三类负荷,加权因子分别为0.08、0.36和0.96,图3 为三类负荷的日负荷曲线.通过设置六种场景说明不同的运行策略对开关优化配置和配电网韧性的影响,如 表2 所示.在这六种场景中,考虑了不同分布式电源容量和采用不同负荷削减方式对韧性提升效果的影响.住宅、商业和工业用户的负荷最大允许削减比例分别为0.5、0.3和0. ...
基于POP NSGA-Ⅱ的配电网故障恢复重构
1
2018
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
基于POP NSGA-Ⅱ的配电网故障恢复重构
1
2018
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
Coordinating multiple sources for service restoration to enhance resilience of distribution systems
1
2018
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
含光伏电源的配电网故障定位策略研究
1
2015
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
含光伏电源的配电网故障定位策略研究
1
2015
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
考虑负荷控制的有源配电网故障恢复策略
1
2017
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
考虑负荷控制的有源配电网故障恢复策略
1
2017
... 目前,已经有一些学者开展了利用分布式电源和开关设备相配合提升配电网韧性的研究[3 ] .通常是在配电网故障后,改变开关状态[4 ] 形成多个以分布式电源为供电核心的微电网,恢复关键负荷供 电[5 ] .以上研究表明了正确配置开关设备对于快速隔离故障,缩小故障区域具有重要影响[6 ] ,与分布式电源相配合能够有效提高配电网韧性[7 ] . ...
Four rules to help locate protective devices
1
1991
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
基于LCC和改进BDE法的配电网开关优化配置
1
2015
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
基于LCC和改进BDE法的配电网开关优化配置
1
2015
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
配电自动化终端布局规划方法
1
2016
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
配电自动化终端布局规划方法
1
2016
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
Multi-objective optimization algorithm for switch placement in radial power distribution networks
1
2015
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
适应自愈要求的配电网开关优化配置
1
2016
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
适应自愈要求的配电网开关优化配置
1
2016
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
不同网络结构及可靠性要求环境下FTU的最优配置
1
2015
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
不同网络结构及可靠性要求环境下FTU的最优配置
1
2015
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
配电系统开关优化配置的混合整数线性规划模型
2
2018
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
配电系统开关优化配置的混合整数线性规划模型
2
2018
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
Optimized sectionalizing switch placement strategy in distribution systems
3
2016
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
Optimal distribution network automation considering earth fault events
2
2018
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
Financial risk evaluation of RCS deployment in distribution systems
2
2018
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
Considerations of sectionalizing switches in distribution networks with distributed generation
2
2017
... 传统上,配电网规划人员结合历史经验、工程判断和其他相关信息确定开关配置的数量和位 置[8 ] .这种方法虽然简单,但是会导致开关优化配置问题只能得到近似解和非最优解.后来有学者通过贪心算法[9 ] 、遗传算法[10 ,11 ] 、蚁群算法[12 ] 和粒子群算法[13 ] 等启发式方法进行了更精确的研究以解决该问题,但同样无法保证全局最优解,并且在大规模系统中实施会有较大的计算负担.因此,又有学者利用数学规划的方法寻找最佳解决方案[14 ,15 ,16 ,17 ,18 ] .文献[14 ,15 ]提出了一种基于混合整数线性规划模型的优化方法解决配电网中开关优化配置问题;文献[16 ]在文献[15 ]的基础上进一步考虑了接地故障对开关优化配置的影响.但是上述研究中元件故障率均采用统计值,无法体现出极端灾害下元件故障的随机性.文献[17 ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
... ]考虑了故障发生的随机性,以混合整数线性规划模型的方式提出了配电网自动开关优化配置策略,但是建立的模型仅能适用于单重故障下的负荷停电量计算,不能适应极端灾害下配电网常发生的多重故障;文献[18 ]在开关优化配置问题中考虑了分布式电源的影响,但分布式电源仅配置在配电网末端,实际上分布式电源可以接入配电网任意位置,其模型不具备实用性. ...
电网的弹性建模与评估
1
2015
... (2) 更新配电网结构,计算当前状态下的系统功能,生成最优故障抢修策略[19 ] . ...
电网的弹性建模与评估
1
2015
... (2) 更新配电网结构,计算当前状态下的系统功能,生成最优故障抢修策略[19 ] . ...
A reliability test system for educational purposes-basic distribution system data and results
1
1991
... 首先通过图2 中简单的测试算例对配电网开关优化配置问题进行说明,再通过典型的RBTS4算 例[20 ] 说明模型的有效性.本文侧重于对提升配电网韧性的开关优化配置模型研究,并未对灾害建模进行深入研究,因此选用文献[3 ]中的台风灾害模型和强度.测试算例中包含住宅、商业和工业三类负荷,加权因子分别为0.08、0.36和0.96,图3 为三类负荷的日负荷曲线.通过设置六种场景说明不同的运行策略对开关优化配置和配电网韧性的影响,如 表2 所示.在这六种场景中,考虑了不同分布式电源容量和采用不同负荷削减方式对韧性提升效果的影响.住宅、商业和工业用户的负荷最大允许削减比例分别为0.5、0.3和0. ...