1 引言
本文在原有多重叠加逆变装置的基础上进行改进,提出了一种由圆形移相变压器构成的谐波注入式逆变装置。该逆变装置包含一个主逆变器、一个辅助逆变器组和圆形移相变压器。主逆变器由一个三相半桥逆变电路构成,通过圆形变压器直接向负载供电,辅助逆变器组由两个三相半桥逆变电路构成,产生设定相位和宽度的谐波脉冲,谐波脉冲通过圆形变压器的旋转磁场原理作用到主逆变器的输出电压上,使输出电压中的谐波成分被抵消,得到逼近正弦的输出波形。
这种逆变装置结构中,主逆变器的功率为基波功率和谐波功率之和,辅助逆变器组的功率主要为5次7次谐波功率之和,圆形移相变压器的功率与辅助逆变器组相等,因此两者的功率均不及主逆变器的1/10。相比于采用多重叠加原理的逆变装置,谐波注入式逆变装置大大降低了系统总重量和体积。由于辅助逆变器开关器件电流、电压等级很低,不会因为增加开关器件而增加成本。
2 逆变装置的结构和原理
2.1 圆形变压器
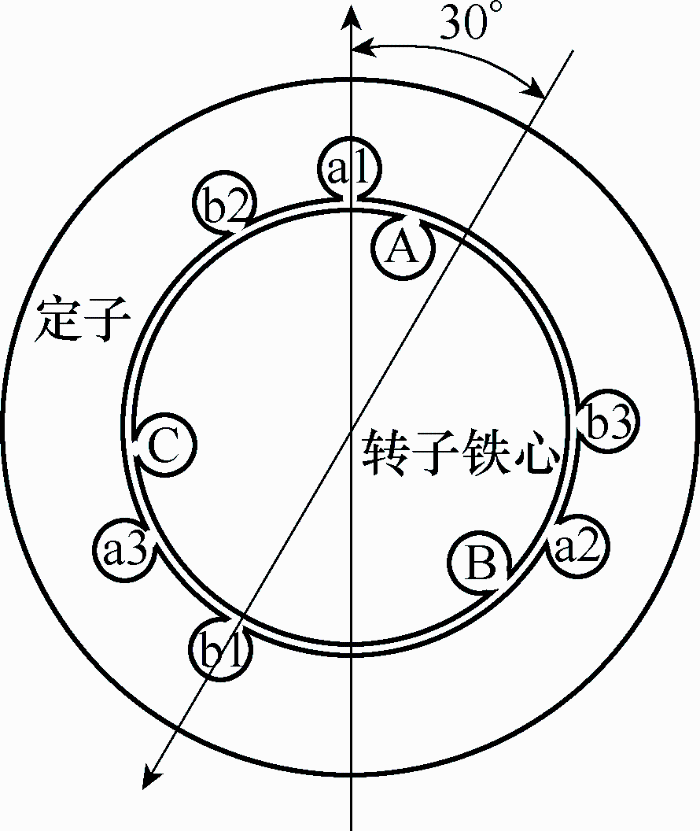
圆形移相变压器的电磁结构类似与绕线式感应电机,但转子通过机械方式堵转固定。根据感应电机原理,定转子之间可以通过电磁感应实现电能传递。圆形移相变压器共有三套对称绕组:ABC、a1b1c1和a2b2c2。ABC在转子上,a1b1c1和a2b2c2在定子上。转子外表面开24个槽,定子内表面开24个槽,内部铁心槽与外部铁心槽对齐,以减小漏磁通和磁路磁阻。转子和定子每个极距下的两个线圈为串联连接,输入a1相、a2相和输出A相分别由两个槽内线圈串联而成。为了消除5、7次谐波,使定子上两套绕组a1b1c1和a2b2c2在空间上相移30°,但第一套绕组a1b1c1正向输入一组6阶梯波电压,第二套绕组a2b2c2反相输出一组6阶梯波电压,因此两套绕组同名端相反,圆形变压器的结构示意图如图1所示,转子上绕组ABC在空间上与第一套绕组a1b1c1相移15°,即位于定子上两套绕组中间位置。
图1
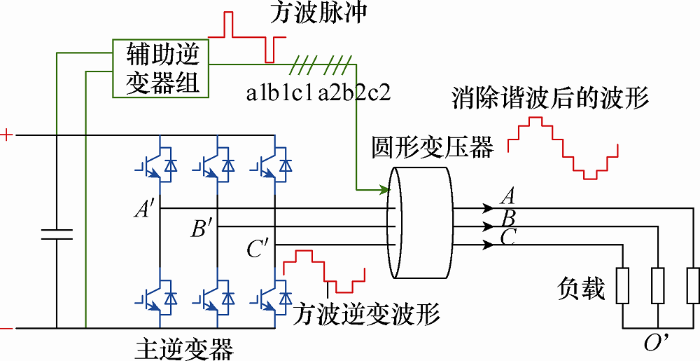
2.2 逆变装置的原理
图2
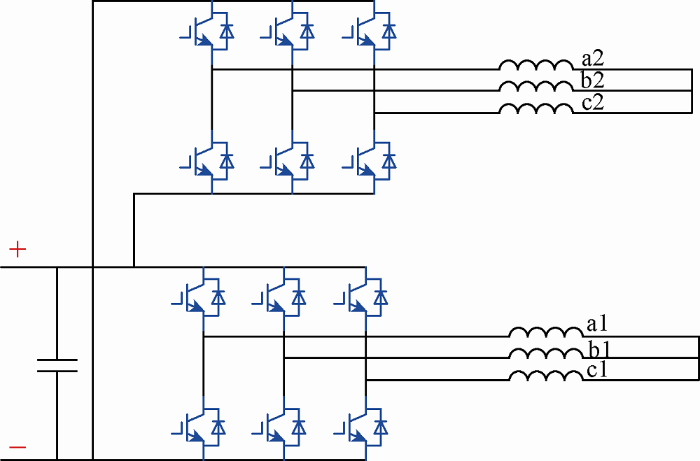
图3
3 谐波消除原理
在六相感应电机中,通过时间、空间的相位关系的选取,可以消除定子磁动势中的5、7次谐波,同时加强基波磁动势,从而消除6次基频的脉动转矩。而在这里我们将利用圆形移相变压器获得相反的结果,即消除定子磁动势中的基波磁动势,加强5、7次谐波。
当目标消除谐波为5次和7次谐波时,将辅助逆变器组中两个半桥逆变电路输出的三相方波脉冲电压设为30°脉宽,相位差也设置为30°。第1套对称三相绕组a1b1c1方波脉冲电压可表示为
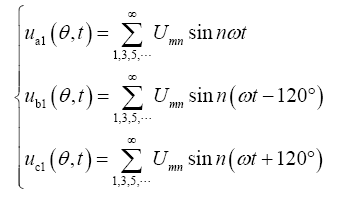
一般这组三相电压除基波外会包含各奇次谐波,谐波幅值${{U}_{mn}}$和脉冲宽度$\theta $有关。根据旋转磁场理论,产生的绕组电流会建立除3的倍数次谐波外各次谐波的旋转磁场。设基波电流和主要谐波电流产生的空间矢量磁动势分别为F1,1、F1,5、F1,7、…。
依据谐波理论我们知道基波磁动势以ω的角速度顺时针旋转,5次谐波磁动势以5ω的角速度逆时针旋转,7次谐波磁动势以7ω的角速度顺时针旋转。
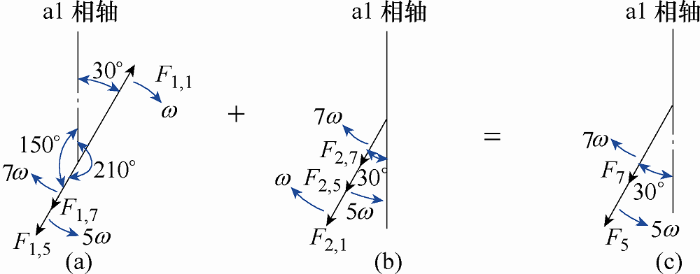
基于圆形变压器的结构特点,并且在输入电压相位设置上第2套绕组滞后第1套绕组30°。第1套绕组a1b1c1的基波磁动势旋转30°时第2套绕组a2b2c2刚开始产生磁动势。图4a为第1套绕组a1b1c1所产生的基波磁动势F1,1转过a1相轴30°时刻,5次和7次谐波磁动势F1,5和F1,7矢量的空间位置。其中ω代表基波磁动势的旋转角速度。此时,第2套绕组a2b2c2刚好产生另一组磁动势F2,1、F2,5、F2,7、…。图4b为同一时刻F2,1、F2,5、F2,7矢量的空间位置。比较图4a和4b,可知两个基波磁动势F1,1和F2,1反相,而5次和7次谐波磁动势同向,叠加后可以得到如图4c所示的空间矢量磁动势F5和F7。
图4
基于此时刻之后的任意时刻,由于两套绕组的输入参数是一致的,产生的基波以及各次谐波磁动势幅值分别相同,旋转方向不变,角速度恒定,故在任意时刻,基波都会抵消,5、7次谐波得到增强。
通过以上分析,可以证明,通过时间、空间相位关系和绕组同名端的选取,可以在圆形变压器中消除基波磁动势,而使5、7次谐波磁动势增强。根据交流电磁场理论,定子绕组产生的5、7次谐波磁动势将在转子绕组上产生相应的磁动势,从而消除转子磁动势中的谐波。
4 逆变装置设计和有限元分析
4.1 数学模型
圆形移相变压器的绕组分布如图1所示,定子绕组为变压器的一次侧,转子绕组为变压器的二次侧。设转子绕组所接负载阻抗为${{Z}_{L}}={{r}_{L}}+j\omega {{l}_{L}}$。
图1所示6个绕组电路的电压方程矩阵为
其中,U、I、R分别表示圆形移相变压器的电压矢量、电流矢量和电阻矩阵,可分别表示为
$\left\{ \begin{align} & \mathbf{U}={{({{u}_{\text{a}1}}\text{ }{{u}_{\text{b}1}}\text{ }{{u}_{\text{c}1}}\text{ }{{u}_{\text{a}2}}\text{ }{{u}_{\text{b}2}}\text{ }{{u}_{\text{c}2}}\text{ }{{u}_{\text{A}}}\text{ }{{u}_{\text{B}}}\text{ }{{u}_{\text{C}}})}^{\text{T}}} \\ & \mathbf{I}={{({{i}_{\text{a}1}}\text{ }{{i}_{\text{b}1}}\text{ }{{i}_{\text{b}1}}\text{ }{{i}_{\text{a}2}}\text{ }{{i}_{\text{b}2}}\text{ }{{i}_{\text{c}2}}\text{ }{{i}_{\text{A}}}\text{ }{{i}_{\text{B}}}\text{ }{{i}_{\text{C}}})}^{\text{T}}} \\ & {{\mathbf{R}}_{T}}=\text{diag}{{({{r}_{T}}\text{ }{{r}_{T}}\text{ }{{r}_{T}}\text{ }{{r}_{T}}\text{ }{{r}_{T}}\text{ }{{r}_{T}}\text{ }0\text{ }0\text{ }0)}^{\text{T}}} \\ \end{align} \right.$
负载的电阻和电感阻抗分别为
$\left\{ \begin{align} & {{\mathbf{R}}_{L}}=\text{diag}(0\text{ }0\text{ }0\text{ }0\text{ }0\text{ }0\text{ }{{r}_{L}}\text{ }{{r}_{L}}\text{ }{{r}_{L}}) \\ & {{\mathbf{L}}_{L}}=\text{diag}(0\text{ }0\text{ }0\text{ }0\text{ }0\text{ }0\text{ }{{l}_{L}}\text{ }{{l}_{L}}\text{ }{{l}_{L}}) \\ \end{align} \right.$
${{u}_{\text{A}}}$,${{u}_{\text{B}}}$,${{u}_{\text{C}}}$为逆变装置中主逆变器的输出电压,${{u}_{\text{a}1}}$,${{u}_{\text{b}1}}$,${{u}_{\text{c}1}}$,…,${{u}_{\text{c}2}}$为辅助逆变器输出的方波电压。当给出绕组互感${{l}_{L}}$和${{l}_{1}}$的值后,即可以列写电感矩阵${{\mathbf{L}}_{T}}$。
4.2 仿真分析
圆形移相变压器的绕组分布如图1所示,定子绕组为变压器的一次侧,有12个线圈,转子绕组为变压器的二次侧,有6个线圈。转子绕组所接为负载阻抗,根据形变压器的电压方程,可以建立仿真模型,主要参数有:rT=2.5 Ω,${{l}_{T}}=0.15\ \text{H}$,${{l}_{1}}=0.01\ \text{H}$,频率$\delta =50\ \text{Hz}$,原二次侧气隙$\delta =0.2\ \text{mm}$,主逆变器和辅助逆变器输入直流电压${{E}_{d}}=25\ \text{V}$。
图5
图6
图7
图8
5 试验验证
为了验证理论和仿真结果,搭建了图9所示的基于圆形移相变压器的谐波注入式逆变装置,圆形移相变压器样机的设计功率为500 W,输入为两套三相星形联结绕组,输出为一套三相星形联结绕组,输入、输出匝比为1:1,为了减小漏电抗且不增大空载电流,气隙定为0.2 mm,定转子铁芯槽口对齐,为了固定转子,用0.2 mm厚绝缘材料垫在定转子气隙间。直流输入电压为25 V。
图9
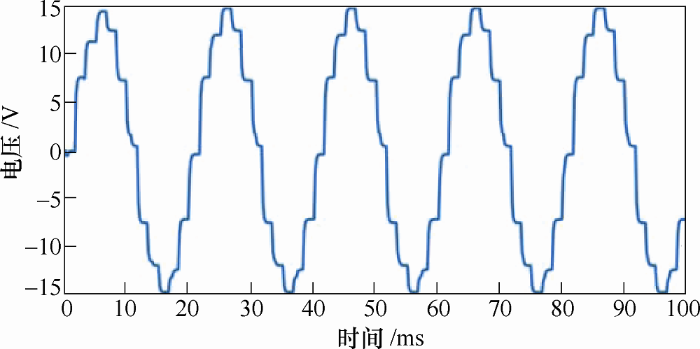
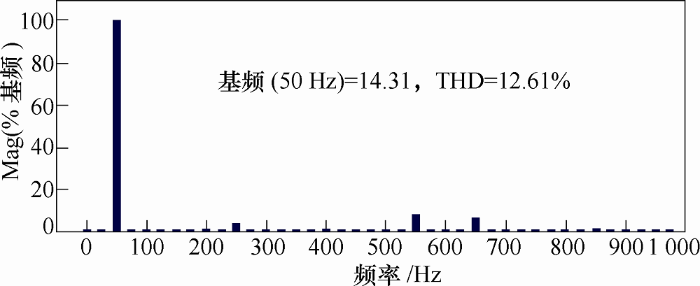
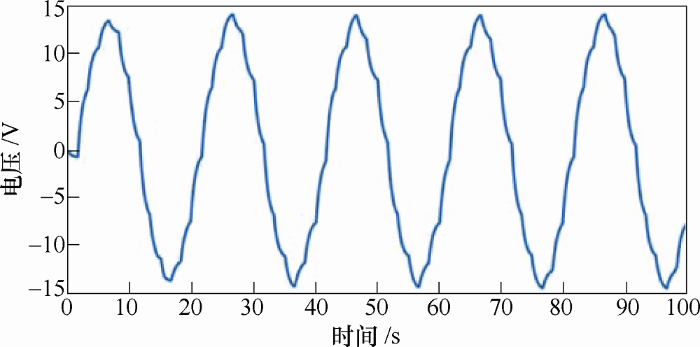
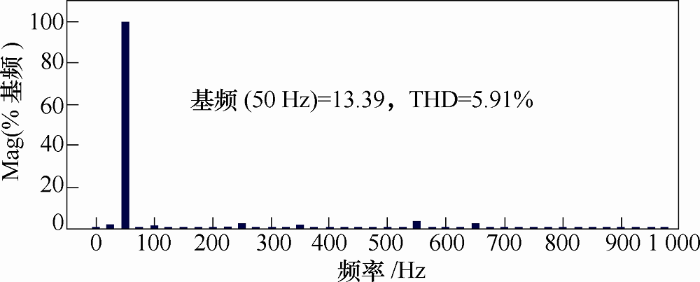
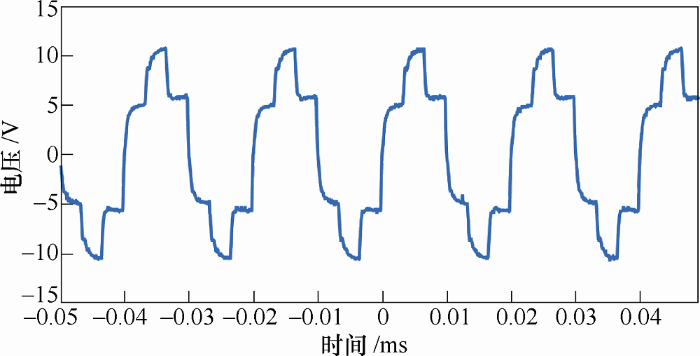
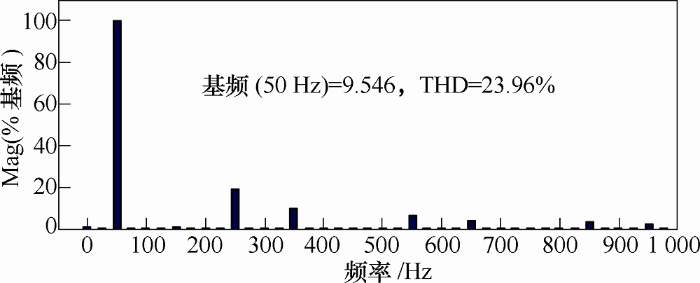
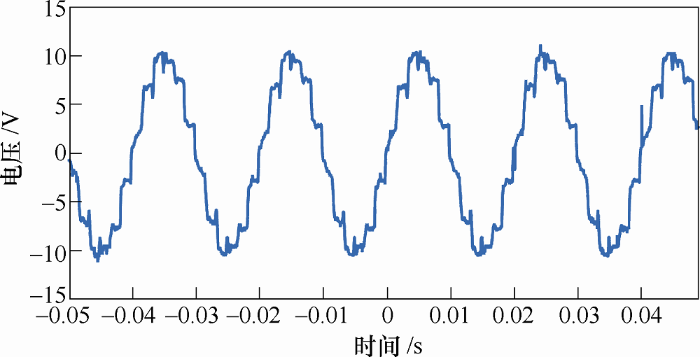
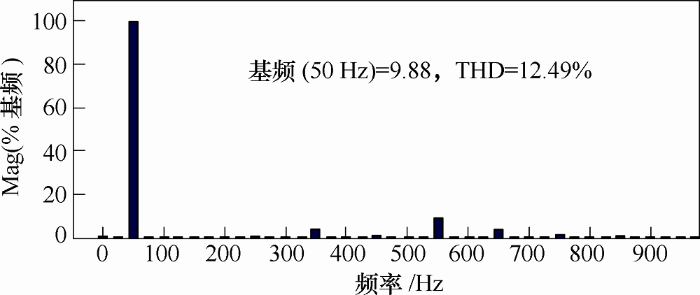
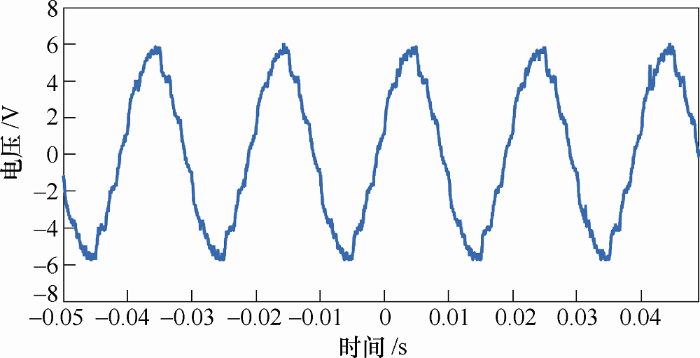
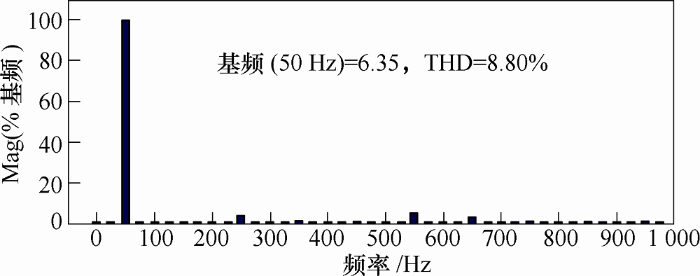
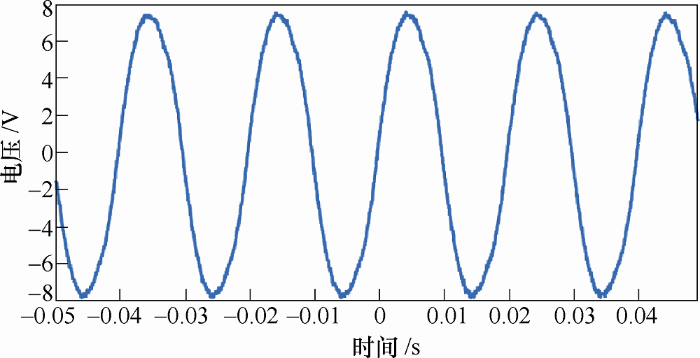
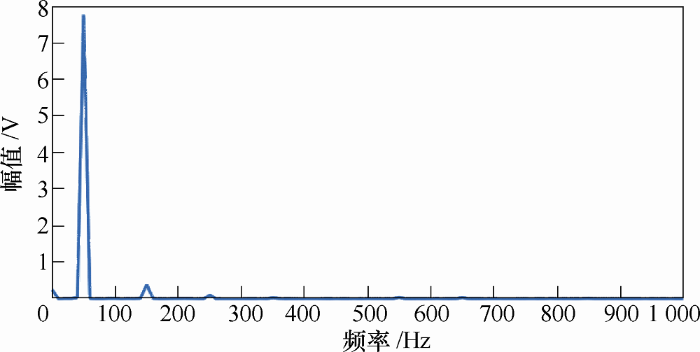
以下结果为试验样机的输出波形。
图10
图11
图12
图13
图14
图15
图16
图17
图18
图19
6 结论
本文基于圆形移相变压器在多重叠加的基础上提出了一种新型逆变装置,通过辅助逆变器产生特定的谐波注入主逆变器的输出电压中,抵消谐波,大大减小了圆形移相变压器的功率。从而在保持谐波消除效果不变的基础上,减小了逆变装置整体的体积和重量,提高了该逆变装置的工程应用价值。通过原理分析、仿真以及试验证明了该新型逆变装置的有效性。
与传统的PWM调制技术相比,此装置可以应用于中大功率系统,而PWM技术诸如SPWM、SVPWM等只能用于小功率的系统中。与传统的移相叠加技术相比,此谐波生成装置只生成谐波并不传递有效功率,所以开关频率远高于移相叠加技术的开关频率,从而提高整个系统的效率。
此装置还可用于解决逆变器以外的谐波问题,比如用于整流电路构成有源滤波器,改善系统电流波形质量,具有巨大的潜在实力。
参考文献
阶梯波合成逆变器的波形调制技术研究
[J].阶梯波合成逆变器开关频率低,谐波含量小,滤波容易,特别适合大功率应用场合,但由于传统阶梯波合成逆变器功率管驱动信号采用延时的方法产生,动态性能差。研究了一种新的阶梯波合成逆变器波形调制技术,采用空间矢量调制方法得到各桥功率管驱动信号,提高逆变器的带宽。在分析移相变压器对空间矢量的影响的基础上,结合阶梯波合成逆变器对驱动信号的逻辑要求,提出从相位滞后通道至相位超前通道顺序采样的错时采样空间矢量调制(space vector modulation,SVM)策略,并分析该调制技术的谐波消除机制和特性。仿真和实验验证了该技术可以用于阶梯波合成逆变器的输出电压的调节,具有优良的输出频谱特性,且增大了逆变器的带宽,有利于提高逆变器的动态性能。
Research on waveform modulation technique for staircase inverters
[J].阶梯波合成逆变器开关频率低,谐波含量小,滤波容易,特别适合大功率应用场合,但由于传统阶梯波合成逆变器功率管驱动信号采用延时的方法产生,动态性能差。研究了一种新的阶梯波合成逆变器波形调制技术,采用空间矢量调制方法得到各桥功率管驱动信号,提高逆变器的带宽。在分析移相变压器对空间矢量的影响的基础上,结合阶梯波合成逆变器对驱动信号的逻辑要求,提出从相位滞后通道至相位超前通道顺序采样的错时采样空间矢量调制(space vector modulation,SVM)策略,并分析该调制技术的谐波消除机制和特性。仿真和实验验证了该技术可以用于阶梯波合成逆变器的输出电压的调节,具有优良的输出频谱特性,且增大了逆变器的带宽,有利于提高逆变器的动态性能。
运用多重化技术改善逆变电源质量的研究
[J].
Research for improving inverse power supply quality with multiplicity technology
[J].
级联型多电平逆变器线电压谐波优化的SVPWM策略研究
[J].级联型多电平逆变器采用载波移相控制可以自然实现各H桥单元功率均衡,开关管开关次数保持一致,而采用同相层叠控制可得到谐波含量更小的线电压,但各H桥单元功率不均衡,开关次数也不一致。本文提出一种结合同相层叠控制和载波移相控制二者优点且实现简单的空间矢量调制策略。通过对电压矢量进行重新组合划分,可以将多电平空间矢量控制算法简化为多个两电平空间矢量的移相叠加。对载波进行重构,可以实现输出线电压谐波更小,同时各H桥单元功率自然实现均衡,开关管开关次数达到一致。搭建了一台三相4.5kW的级联型五电平逆变器,对所提出的SVPWM策略进行了实验验证,实验结果表明所提出的空间矢量调制策略的有效性。
A SVPWM strategy with optimal line-to-line voltage harmonic spectrum for cascaded multilevel inverters
[J].级联型多电平逆变器采用载波移相控制可以自然实现各H桥单元功率均衡,开关管开关次数保持一致,而采用同相层叠控制可得到谐波含量更小的线电压,但各H桥单元功率不均衡,开关次数也不一致。本文提出一种结合同相层叠控制和载波移相控制二者优点且实现简单的空间矢量调制策略。通过对电压矢量进行重新组合划分,可以将多电平空间矢量控制算法简化为多个两电平空间矢量的移相叠加。对载波进行重构,可以实现输出线电压谐波更小,同时各H桥单元功率自然实现均衡,开关管开关次数达到一致。搭建了一台三相4.5kW的级联型五电平逆变器,对所提出的SVPWM策略进行了实验验证,实验结果表明所提出的空间矢量调制策略的有效性。
采用波形合成法的级联式多电平逆变器谐波控制
[J].为改善级联型多电平逆变器输出电压波形质量,对通过控制逆变单元开关角实现级联多电平逆变器谐波控制的方法进行了分析研究。针对解方程组法消除特定谐波中高次多变量方程组难于求解的问题,提出了一种波形合成消除特定谐波的方法。利用此方法可通过简单的三角公式递推计算获得实现特定谐波消除的开关角。依据理论计算结果进行的例证演示列出了开关角所有可能的取值情况,说明通过逆变器开关角的选择可同时实现输出电压中特定谐波的消除及基波幅值的调节。仿真与实验结果验证了该方法的可行性。
Harmonics control for cascaded multilevel inverter applying waveform resultant theory
[J].为改善级联型多电平逆变器输出电压波形质量,对通过控制逆变单元开关角实现级联多电平逆变器谐波控制的方法进行了分析研究。针对解方程组法消除特定谐波中高次多变量方程组难于求解的问题,提出了一种波形合成消除特定谐波的方法。利用此方法可通过简单的三角公式递推计算获得实现特定谐波消除的开关角。依据理论计算结果进行的例证演示列出了开关角所有可能的取值情况,说明通过逆变器开关角的选择可同时实现输出电压中特定谐波的消除及基波幅值的调节。仿真与实验结果验证了该方法的可行性。
基于特定谐波消除PWM的三电平有源中点钳位逆变器共模电压抑制方法
[J].
Suppression method of common-mode voltage for three-level active neutral-point-clamped inverter based on selective harmonics elimination PWM
[J].
阶梯波合成逆变器的单脉宽调制调压技术研究
[J].
Research on staircase waveform inverters with single-pulse width modulation technology
[J].
Control of cascaded transformer multi-level inverter based DSTATCOM
[J].
高性能大容量交流电机调速技术的现状及展望
[J].
High performance and high power AC motor variable speed drives statusand trends
[J].
用于多重化逆变的移相变压器
[J].在多重化逆变中, 需要移相变压器把多相逆变器输出的非正弦电压进行合成, 使输出电压为接近正弦的多阶梯波形。为了改善结构和电气性能, 该文提出了一种新型磁路结构的移相变压器, 和普通移相整流变压器相比, 新型变压器铁心为圆形结构, 整体结构更为紧凑和对称, 电路结构更为简单。针对双Y/Y绕组变压器, 理论证明了5次、7次等主要低次谐波被消除, 合成磁动势为一接近圆形的旋转矢量, 并数值仿真分析了不同类型谐波电流所生成的磁场的性质。给出了由新型变压器构成的多重化逆变器的数学模型并对基本特性进行了仿真。最后, 基于多重化逆变系统, 实验验证了新型移相变压器的有效性, 结合设计对主要性能进行了分析。
A phase-shift transformer applied in multi-module inverters
[J].在多重化逆变中, 需要移相变压器把多相逆变器输出的非正弦电压进行合成, 使输出电压为接近正弦的多阶梯波形。为了改善结构和电气性能, 该文提出了一种新型磁路结构的移相变压器, 和普通移相整流变压器相比, 新型变压器铁心为圆形结构, 整体结构更为紧凑和对称, 电路结构更为简单。针对双Y/Y绕组变压器, 理论证明了5次、7次等主要低次谐波被消除, 合成磁动势为一接近圆形的旋转矢量, 并数值仿真分析了不同类型谐波电流所生成的磁场的性质。给出了由新型变压器构成的多重化逆变器的数学模型并对基本特性进行了仿真。最后, 基于多重化逆变系统, 实验验证了新型移相变压器的有效性, 结合设计对主要性能进行了分析。
用于多脉波整流的直线式移相变压器
[J].
A linear-shaped phase-shift transformer applied in multi-pulse rectifier
[J].
圆形变压器在24脉波整流系统中的应用
[J].
Application of round-shaped transformers in 24 pulses rectifier systems
[J].
用于抑制多相异步电动机定子谐波电流电抗滤波器的研究
[J].
Study of novel filter for reducing harmonic currents of stator windings in multi-phase induction motor
[J].
一种用于多重叠加逆变的圆形移相变压器
[J].
A round shape phase-shift transformer applied in multi-module inverter
[J].