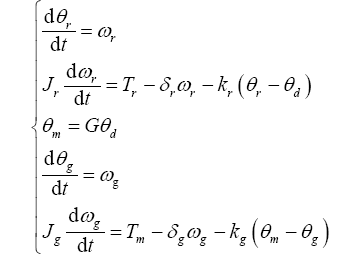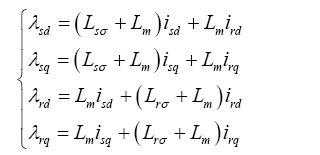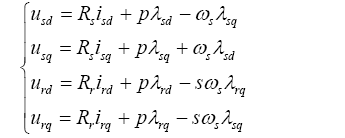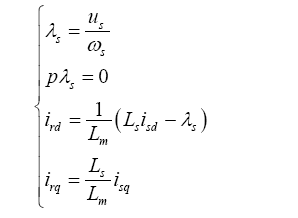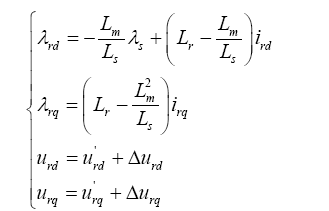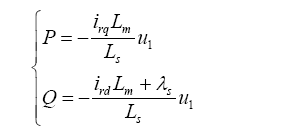1 引言
风能是太阳能的一种转换形式,是取之不尽、用之不竭的绿色可再生能源。风力发电是一种主要的风能利用形式,截止2018年底,中国风电累计并网容量已达1.84亿千瓦,稳居世界第一。
由于我国风力发电具有大规模、集中接入的特点,风力发电机组的电网友好性对电网安全的影响越来越显著,特别是故障穿越性能。因此,研究风力发电机组的并网特性和改善其稳定电网的能力是风力发电技术中重要的课题[1 ,2 ,3 ] 。
2 风电机组故障穿越的现状
我国前期出现的风电机组故障脱网的主要原因,一是风电机组不具备低电压穿越能力而脱网,二是由于故障清除后机组无功功率响应滞后引起的高电压而脱网,三是故障中风电机组瞬间吸收大量无功功率引起电网故障恶化而导致的脱网。
保证风电机组在低电压穿越过程中不脱网运行是对机组的最基本要求,为改善风电机组电网友好性,机组在不脱网的同时还要发送适量的无功功率。多起电网事故后都出现了高电压的情况,就是无功补偿过量造成的。由此可见,优化风电机组在不同的故障穿越情况下的响应行为对电网故障恢复的影响至关重要[4 ,5 ,6 ] 。
为更好地改善风机脱网问题,必须在风电机组优化低电压穿越特性的基础上,科学合理地解决无功调用问题。功率分配策略的研究非常重要,而策略研究的关键是建立准确的风机模型[7 ] 。
3 风电机组建模研究
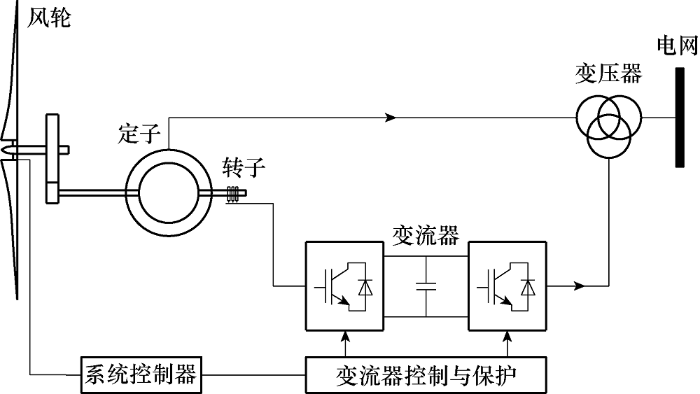
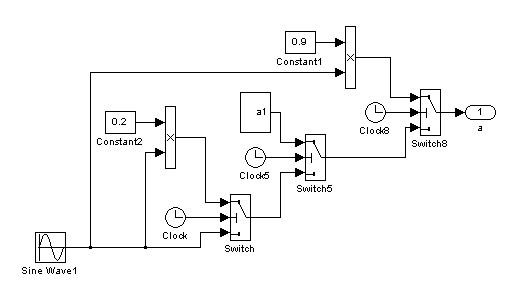
图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] 。
图1
3.1 风轮模型
双馈型风力发电机组根据式(1)将风功率转化为机械能。
(1) ${{P}_{r}}=\frac{1}{2}\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{2}}{{V}^{3}}{{C}_{p}}(\lambda ,\beta )$
式中,ρ 表示空气密度;R 表示风轮半径;V 表示风速;Pr 表示风轮输入功率;Cp (λ ,β )为风能利用系数。
3.2 传动链模型
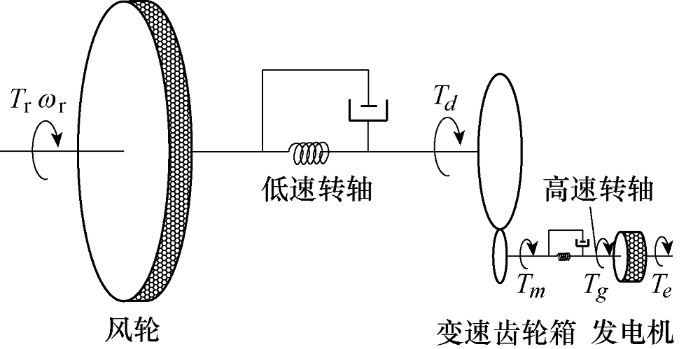
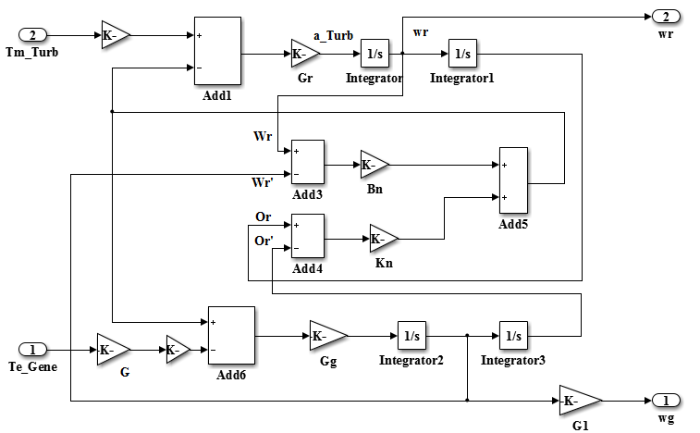
风机机械传动部分包括5部分,即风轮、低速转轴、变速齿轮箱、高速转轴和发电机,如图2 所示[8 , 11 ] 。
图2
(2)
式中,${{\theta }_{r}}$为风轮转角;${{\omega }_{r}}$为风轮角速度;${{J}_{r}}$为风轮转动惯量;${{T}_{r}}$为气动转矩;${{\delta }_{r}}$为低速轴阻尼;${{k}_{r}}$为低速轴刚度;${{\theta }_{d}}$为齿轮箱低速轴转角;${{\theta }_{m}}$为齿轮箱高速轴转角;$G$为齿轮箱传动比;${{\theta }_{g}}$为发电机转角;${{\omega }_{\text{g}}}$为发电机角速度;${{J}_{g}}$为发电机转动惯量;${{\delta }_{g}}$为高速轴阻尼;${{k}_{g}}$为高速轴刚度。其中齿轮箱本身的转动惯量转化到高速轴。
由风轮和传动链共同建立的Simulink模型如图3 所示。
图3
3.3 发电机变流器模型
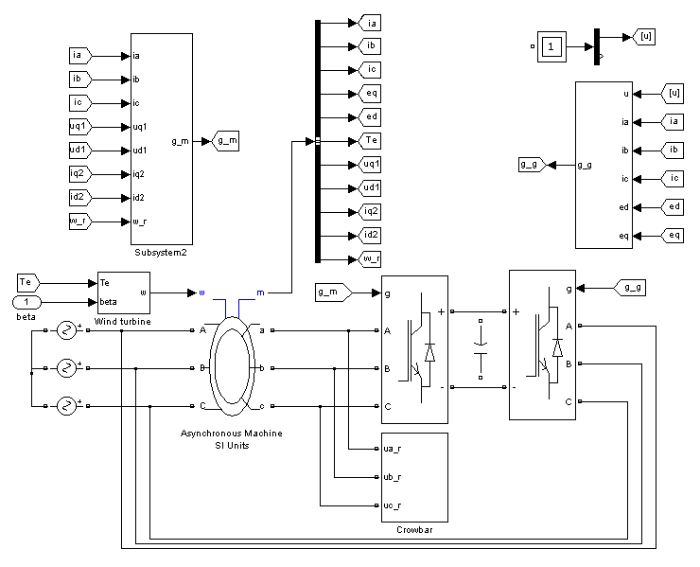
由于低电压穿越持续时间较短且容易产生过电流。为保护IGBT开关不因过载而损坏,保护系统必须能够检测发电机定子、转子回路及电网侧变流器的电流、直流环节电压、电网电压、频率等,当这些量超标时,保护系统就会闭锁变流器。因此研究发电机暂态的电机模型必须能体现这些暂态量。经推导和化简,双馈异步发电机在d -q 同步旋转坐标系下的暂态数学模型[11 ,12 ] 如下所示。
(3)
(4)
(5) ${{T}_{e}}={{\lambda }_{sq}}{{i}_{sd}}-{{\lambda }_{sd}}{{i}_{sq}}$
式中,${{\lambda }_{sd}}$,${{\lambda }_{sq}}$,${{\lambda }_{rd}}$和${{\lambda }_{rq}}$分别为定子绕组和转子绕组合成磁势的d 轴和q 轴分量;${{i}_{sd}}$,${{i}_{sq}}$,${{i}_{rd}}$和${{i}_{rq}}$分别为定子绕组和转子绕组电流的d 轴和q 轴分量;${{u}_{sd}}$,${{u}_{sq}}$,${{u}_{rd}}$和${{u}_{rq}}$分别为定子绕组和转子绕组电压的d 轴和q 轴分量;p 为微分算子;s 为转差率。
式(2)~(4)构成了双馈型风力发电机组的8阶模型。该模型充分考虑了传动部分和发电机部分的动态特性。
变流器使用矢量控制技术实现对双馈发电机的解耦控制,将实际的交流分量分解为有功分量和无功分量,并对这两个分量进行闭环控制。采用定子磁链定向矢量控制时,由定转子的磁链方程和电压方程可以得到矢量控制的原理方程[9 ] 。
(6)
(7)
式中,${{L}_{s}}={{L}_{s\sigma }}+{{L}_{m}}$,${{L}_{r}}={{L}_{r\sigma }}+{{L}_{m}}$。$u_{rd}^{'}$,$u_{rq}^{'}$分别为${{i}_{rd}}$,${{i}_{rq}}$具有一阶微分关系的电压分量,$\Delta {{u}_{rd}}$,$\Delta {{u}_{rq}}$分别为电压补偿分量。
(8)
发电机与变流器主电路和控制电路的Simulink模型如图4 所示。
图4
3.4 主控模型
风力发电机组是通过控制发电机的转矩来实现机组按最优转速运行的。主控系统首先检测发电机转速,然后根据控制策略给定变流器输出转矩。
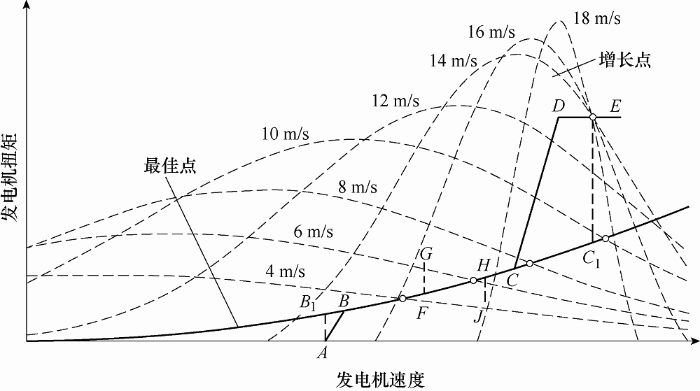
风力发电机组转矩与转速的关系如图5 所示:在低风速B1、C1阶段,风机保持最佳桨距角。机组处于吸收能量欠饱和状态,机组的控制目标是尽可能多地利用风能。在最佳桨距角状态下保持最佳叶尖速比,在任意风速下都能追踪到最大的风能利用系数。风功率与转速关系通过变换式(1)可得
(9) ${{P}_{r}}=\frac{1}{2}{{C}_{p}}(\lambda ,\beta )\frac{\rho \text{ }\!\!\pi\!\!\text{ }{{R}^{5}}}{{{G}^{3}}{{\lambda }^{3}}}{{\omega }^{3}}={{K}_{\lambda }}{{\omega }^{3}}$
图5
(10) ${{T}_{r}}={{K}_{\lambda }}{{\omega }^{2}}$
低风速期间采用直接转矩控制,但由于风轮转动惯量的影响,转速变化很难跟上风速的变化,机组转动惯量越大低风速期间能量捕获越困难。
在中等风速C1 、E阶段,机组达到额定转速,转矩PI控制器根据发电机转速改变转矩,使发电机转速稳定在额定值的一定范围内,以实现转速对转矩和功率的软响应。转矩PI控制器拉普拉斯变换公式如下
(11) $\frac{{{K}_{q}}}{s{{T}_{q}}}\left( 1+s{{T}_{q}} \right)$
式中,${{K}_{q}}$为比例常数,${{T}_{q}}$为积分时间常数,积分增益是${{K}_{q}}/{{T}_{q}}$。
高风速阶段处于吸收能量过饱和阶段,需限制功率输入,拟制功率波动。限制功率的方法可降低风功率利用系数${{C}_{p}}$,或者通过偏航减少风机受风面积。高风速以上的非线性使确定控制器的增益十分困难,可采用查表法来确定控制器的增益。变桨控制算法的拉普拉斯形式如下
(12) $\frac{K\left( \beta \right)}{s{{T}_{i}}\left( \beta \right)}\left( 1+s{{T}_{i}}\left( \beta \right) \right)$
为防止齿轮箱的扭转振动,可以通过修改发电机的转矩给定获得一个纹波转矩,增大传动链的阻尼。纹波力矩的大小与转速变化率呈正比。附加转矩信号由一个带通滤波器获得,带通滤波器的形式如下
(13) $K\frac{2\zeta \omega s}{{{s}^{2}}+2\zeta \omega s+{{\omega }^{2}}}$
信号经过带通滤波器后再经过两个陷波器:第一个陷波器用于屏蔽3P,第二个陷波器用于屏蔽6P,陷波器的传递函数如下
(14) $\frac{{{s}^{2}}+2{{\zeta }_{1}}{{\omega }_{1}}s+{{\omega }_{1}}^{2}}{{{s}^{2}}+2{{\zeta }_{2}}{{\omega }_{2}}s+{{\omega }_{2}}^{2}}$
如图5 所示在高风速阶段,转矩控制和变桨控制器有可能耦合在E点,为使两者解耦,风机的转矩控制曲线由AB1 C1 E修正为ABCDE运行。
图6
3.5 风电机组低电压穿越故障建模及解决方案
低电压穿越的基本要求是:(1) 风电机组具有在并网点电压跌落至20%额定电压时能够保证不脱网连续运行625 ms的能力。(2) 并网点电压在发生跌落后2 s内恢复到额定电压90%时,风电机组能够保证不脱网连续运行。低电压穿越的故障模型如7所示。
图7
为实现机组能安全不脱网运行。有两种解决途径:一是改进控制策略,此方法没有额外成本,但是在故障严重时仅靠改进控制策略很难满足要求。当电压跌落比较深时,必须采用第二种方法:增加硬件电路。
改进控制策略时,可以采用在原有控制上加入静止无功补偿器、用反电动势抑制定子磁链的直流分量或者负序分量引起的转子过电流、采用鲁棒控制技术的控制器等来实现精确控制。
增加硬件电路时,可以采用增加转子侧的撬棒电路、增加直流侧的卸荷电路等方法,工程中常用的方法是在转子侧增加撬棒电路[15 ] 。
4 仿真分析
以某双馈型风电机组为例,按照第3节的模型研究,搭建基于Matlab软件的仿真模型,研究其在 电网故障下的风电机组运行特性[16 ,17 ] 。风电机组的主要参数见表1 。
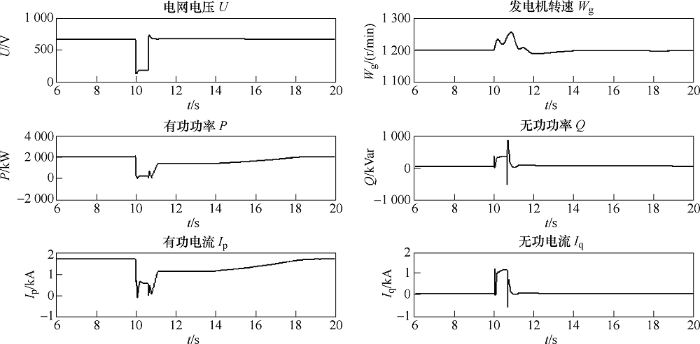
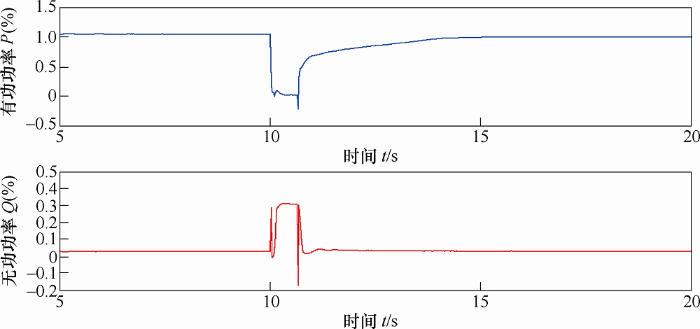
基于电网阻抗分压原则,设置电网的短路阻抗和限流阻抗,来模拟电网电压的跌落深度。假定在风电机组满功率运行的情况下,第10 s的时刻电网高压侧(35 kV)发生三相20%电压跌落故障,故障持续时间为625 ms。其电网故障的参数如表2 所示。电网发生三相对称短路故障,电压跌落20%的仿真结果如图8 所示。
图8
图8
满功率情况下,电压三相对称跌落20%的仿真结果
(1) 当电网电压跌落至20%时,由于变压器和线路阻抗的共同作用,风电机组出口处电压瞬时跌落至20%以下,幅值在5%左右;由于风电机组的电气特性响应很快,在100 ms以内,机组出口处的电压在风电机组的无功支撑下将提升至20%以上。
(2) 风电机组的发电机转速在电网发生短暂故障时出现转速振荡,故障期间转速会快速提升,但不至于发生因超速而停机的情况。风电机组的惯量可拟制转速的快速提升。
(3) 电压跌落过程中,风电机组可按要求发出无功功率支撑电网电压,还可提供部分的有功支撑电网频率。
(4) 电网电压跌落深度为20%时,机组支撑电网的时间不少于625 ms。
(5) 电网电压瞬间恢复时,无功功率输出瞬时消失,在电网故障消除10 s内,有功功率输出恢复正常。
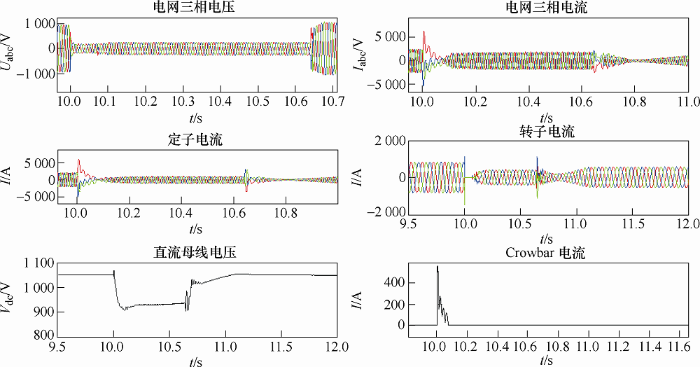
变流器是风电机组实现低电压穿越的核心部件,由于电网电压突变很容易出现发电机定子过流、转子回路过流、直流母线过压/欠压等情况,这些现象在电网突变瞬间特别明显。如图9 所示,在电网电压跌落20%的情况下,发电机的动态模型准确反映了在低穿过程中风电机组的机电暂态和稳态特性[5 ,6 ] 。
图9
图9
电压跌落20%情况下,发电机的动态响应仿真结果
(1) 电网电压跌落瞬间定子电流突增,超过门限值后立即触发Crowbar电阻动作,卸掉多余的电流,保证了发电机定子安全。同时,转子电流也出现变化,但幅度不大。
(2) 随着电网电压跌落直流母线电压因外部电网电压降低而降低。由于网侧变流器控制效果显著,直流母线电压未发生波动,风电机组有功功率和无功功率输出保持稳定。
(3) 电网电压开始恢复时直流母线电压出现了振荡,导致转子电流出现大的波动,但均没有超过门限值;随着电网的电压的逐渐恢复,直流母线电压得到控制,转子电流波形畸变消失,输出功率平缓增加,低穿过程逐渐结束。
5 故障行为优化仿真与试验验证
风电机组故障行为研究始于德国E.ON能源公司关于电网故障导致风电机组脱网的分析报告,报告指出电压跌落到一定深度的电网故障会导致整个电网的所有风电机组脱网,进而导致区域性电网崩溃事故。风电机组的低电压穿越特性一直是故障行为分析的核心研究领域,包括故障前状态对故障行为的影响,故障发生时的暂态过程中的电气量突变,故障期间以及故障恢复时有功功率和无功功率特性对电网和风电机组的影响等方面。
暂态过程中的电气突变,主要是指在电网故障发生和恢复时刻,由电力电子器件的机电耦合而产生的尖峰电流,其值的大小与电力电子的特性有密切关系,往往具有一定的随机性;稳态过程的功率恢复水平,体现在电网电压正常后,风电机组有功功率和无功功率快速稳定地恢复到电网跌落前的能力。有功功率恢复特性的优劣取决于两方面:一是功率恢复的平稳性,二是功率恢复的时效性。当出现功率恢复不平稳时,机组可通过调节主控制器中的转矩控制环使转矩输出平稳。同时,改进变流器控制的内部结构和调整其算法参数亦能提高功率的响应速度。无功功率需要在电网恢复正常时快速降为零,避免因无功支撑过剩而造成电网电压过高。
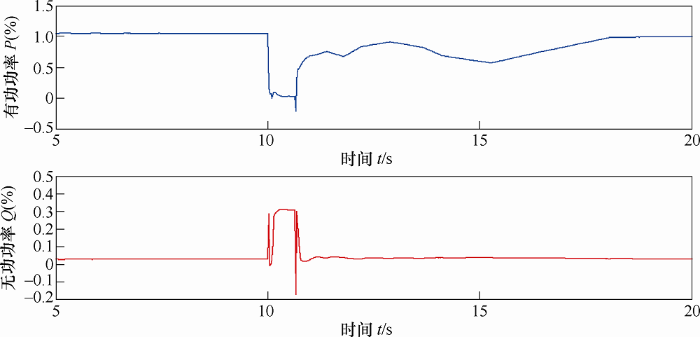
通过图10 可以看出,在策略优化前,电网电压跌落和恢复瞬间,无功功率均有一个较大的冲击电流,在电网电压恢复之后,无功功率能在规定的时间内降至0,但有功功率恢复比较缓慢且有大幅度的波动。策略优化后改善效果明显如图11 所示。
图10
图11
为验证效果,课题组针对某型风电机组开展低电压穿越现场试验。试验采用基于阻抗分压原理的固定式低电压穿越测试设备,串接在风电机组出口变压器高压侧,通过选择匹配的阻抗值产生不同幅度的电压跌落。电压跌落期间残余电压分别设置为90%U n ,75%U n ,50%U n ,35%U n 和20%U n ,测试风电机组在小功率输出(0.1P n ≤P ≤0.3P n )和大功率输出(P >0.9P n )两种工况下,风电机组出口变压器高压侧发生三相短路和两相短路故障时风电机组的低电压穿越特性。
主要测试分析参数有风电机组出口变压器高压侧和低压侧的电压、有功电流、无功电流、有功功率、无功功率,以及风速、发电机转速和桨距角。其中电压、电流和功率的计算采用基波正序法,风速、发电机转速和桨距角由实测值平滑滤波得到。
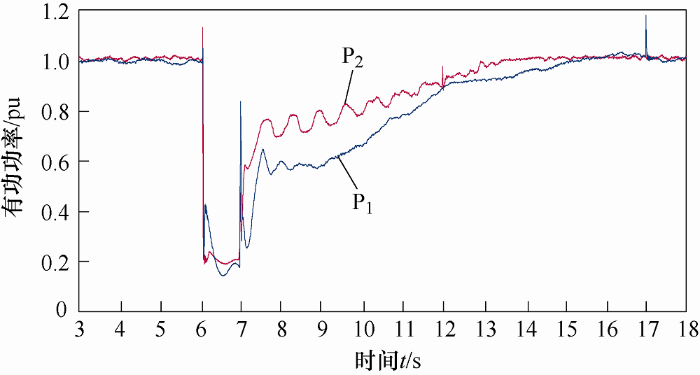
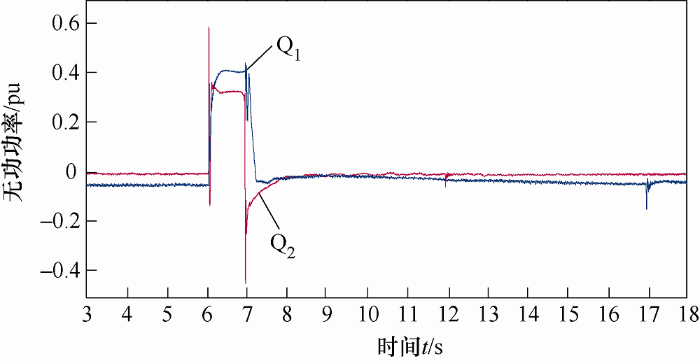
测试风电机组位于国家能源大型风电并网系统研发(实验)中心张北风电试验基地,以电网电压三相对称跌落至35%U n ,大风功率(P >90%P n )测试试验工况为例,优化前后方案实测波形如图12 、图13 所示。其中,P1 为方案优化前测试波形,P2 为方案优化后测试波形。
图12
图13
由图12 可知,策略改进前的风电机组,在6.95 s故障切除时有功功率为360 kW(0.18 p.u.),在15.5 s时有功功率恢复至故障前的值1 980 kW(0.99 p.u.),耗时8.55 s;策略改进后的风电机组,自6.95 s即故障切除时有功功率为420 kW(0.21 p.u.)起至13.47 s时有功功率恢复至故障前的值2 040 kW(1.02 p.u.),耗时6.52 s。由图13 可得,策略改进前的风电机组动态无功电流响应时间为56 ms;策略改进后的风电机组动态无功电流响应时间为47.3 ms。该型风电机组在故障期间动态无功支撑响应时间提高10%以上,故障后有功功率恢复速率提高20%以上,优化效果非常明显。
6 结论
本文通过对双馈型风力发电机组各部件运行原理的研究,建立了机组的数学模型和Simulink仿真模型。仿真验证了本研究模型的正确性,同时针对现阶段比较突出的低电压穿越问题,分析了风电机组在电网故障情况下的动态特性。基于仿真和试验数据,针对低电压穿越故障后风电机组有功功率恢复较慢和无功支撑不理想的情况,通过改进主控制器和变流器的控制策略,整定和优化了新的控制参数,从而改善了风电机组的低电压穿越性能,加快了有功功率的恢复速度,改善了电网友好性。本研究对低电压穿越能力验证和未来电网稳定性分析都有重要的参考价值。
参考文献
View Option
[1]
李建林 , 许洪华 , 等 . 风力发电中的电力电子变流技术 [M]. 北京 : 机械工业出版社 , 2008 .
[本文引用: 1]
[2]
李建林 , 许洪华 , 等 . 风力发电系统低电压运行技术 [M]. 北京 : 机械工业出版社 , 2008 .
[本文引用: 1]
[3]
赵清声 , 王志新 . 双馈风力风电机组系统接入与稳定运行仿真
[J]. 电网技术 , 2007 ,31 (22 ):69 -74 .
Magsci
[本文引用: 1]
<p>分析了包含大量异步风力发电机组的风电场并网运行后对电力系统静态和动态稳定性的影响。从系统接入和稳定运行的角度研究了双馈风力发电机组及普遍采用的定子磁链定向矢量控制策略在提高风电系统稳定性方面的优势与不足。以实际机组为例在PSCAD/EMTDC平台上建立了仿真模型,结果表明双馈风力发电机组在风速发生变化时不仅能够以变速恒频方式运行并追踪最大风能,且电网电压也比传统鼠笼式风力发电机组更为稳定。在系统发生最严重的三相接地故障时,风电场具有更好的暂态稳定性。</p>
Zhao Qingsheng Wang Zhixin . Simulation of doubly-fed wind turbine system access and stable operation
[J]. Power System Technology , 2007 ,31 (22 ):69 -74 .
Magsci
[本文引用: 1]
<p>分析了包含大量异步风力发电机组的风电场并网运行后对电力系统静态和动态稳定性的影响。从系统接入和稳定运行的角度研究了双馈风力发电机组及普遍采用的定子磁链定向矢量控制策略在提高风电系统稳定性方面的优势与不足。以实际机组为例在PSCAD/EMTDC平台上建立了仿真模型,结果表明双馈风力发电机组在风速发生变化时不仅能够以变速恒频方式运行并追踪最大风能,且电网电压也比传统鼠笼式风力发电机组更为稳定。在系统发生最严重的三相接地故障时,风电场具有更好的暂态稳定性。</p>
[4]
梁亮 . 双馈感应式风力发电系统低电压穿越能力研究
[D]. 北京:中国科学院电工研究所 , 2007 .
[本文引用: 1]
[5]
舒思婉 . 双馈电机低电压穿越时的暂态特性研究
[D]. 北京:华北电力大学 , 2016 .
[本文引用: 2]
[6]
毕天姝 , 刘素梅 , 薛安成 , 等 . 具有低电压穿越能力的双馈风电机组故障暂态特性分析
[J]. 电力系统保护与控制 , 2013 (2 ):26 -31 .
[本文引用: 2]
Bi Tianshu Liu Sumei Xue Ancheng , et al . Fault transient characteristics analysis of doubly fed wind turbines with low voltage ride-through capability
[J]. Power System Protection and Control , 2013 ( 2 ):26 -31 .
[本文引用: 2]
[7]
张可达 . 风电机组模型建立
[J]. 黑龙江科技信息 , 2016 (25 ):157 -157 .
[本文引用: 1]
Zhang Keda . Establishment of wind turbine model
[J]. Heilongjiang Science and Technology Information , 2016 (25 ):157 -157 .
[本文引用: 1]
[8]
叶杭冶 , 潘东浩 . 风电机组变速与变桨矩控制过程中的动力学问题研究
[J]. 太阳能学报 , 2007 ,28 (12 ):1321 -1328 .
[本文引用: 2]
Ye Hangye Pan Donghao . Research on dynamics of variable speed and variable speed control of wind turbines
[J]. Journal of Solar Energy , 2007 ,28 (12 ):1321 -1328 .
[本文引用: 2]
[9]
高一丹 , 张步涵 . 并网双馈风力发电机组的建模与仿真
[J]. 湖北工业大学学报 , 2010 ,25 (1 ):75 -80 .
[本文引用: 2]
Gao Yidan Zhang Buhan . Modeling and simulation of grid-connected doubly-fed wind turbine
[J]. Journal of Hubei University of Technology , 2010 ,25 (1 ):75 -80 .
[本文引用: 2]
[10]
张照彦 , 马永光 . 双馈异步风力发电机建模与仿真研究
[J]. 电力科学与工程 , 2010 ,26 (1 ):5 -9 .
[本文引用: 1]
Zhang Zhaoyan Ma Yongguang . Modeling and simulation of doubly fed induction wind turbines
[J]. Power Science and Engineering , 2010 ,26 (1 ):5 -9 .
[本文引用: 1]
[11]
陈伯时 . 电力拖动自动控制系统 [M]. 北京 : 机械工业出版社 , 2003 .
[本文引用: 2]
[12]
张兴 . PWM整流器及其控制策略的研究
[D]. 合肥:合肥工业大学 , 2003 .
[本文引用: 1]
[13]
Han A Zhang Z Yin X et al . Study of the factors affected the rotor over-current of DFIG during the three-phase voltage dip
[C]// International Conference on Electric Utility Deregulation & Restructuring & Power Technologies,IEEE , 2008 .
[14]
李智才 , 李凤婷 . 双馈风电机组的建模仿真及其等值方法研究
[J]. 可再生能源 , 2013 ,31 (3 ):31 -35 .
Li Zhicai Li Fengting . Modeling and simulation of doubly fed wind turbines and equivalent methods
[J]. Renewable Energy Resources , 2013 ,31 (3 ):31 -35 .
[16]
M Mohseni S M Islam M A S Masoum Impacts of symmetrical and asymmetrical voltage sags on DFIG-based wind turbines considering phase-angle jump, voltage recovery,and sag parameters
[J]. IEEE Transactions on Power Electronics , 2011 ,26 (5 ):1587 -1598 .
[本文引用: 1]
[17]
Zhou Peng He Yikang Control strategy of an active crowbar for DFIG based wind turbine under grid voltage dips
[C]// Proceeding of International Conference on Electrical Machines and Systems , 2007 : 259 -264 .
[本文引用: 1]
1
2008
... 由于我国风力发电具有大规模、集中接入的特点,风力发电机组的电网友好性对电网安全的影响越来越显著,特别是故障穿越性能.因此,研究风力发电机组的并网特性和改善其稳定电网的能力是风力发电技术中重要的课题[1 ,2 ,3 ] . ...
1
2008
... 由于我国风力发电具有大规模、集中接入的特点,风力发电机组的电网友好性对电网安全的影响越来越显著,特别是故障穿越性能.因此,研究风力发电机组的并网特性和改善其稳定电网的能力是风力发电技术中重要的课题[1 ,2 ,3 ] . ...
双馈风力风电机组系统接入与稳定运行仿真
1
2007
... 由于我国风力发电具有大规模、集中接入的特点,风力发电机组的电网友好性对电网安全的影响越来越显著,特别是故障穿越性能.因此,研究风力发电机组的并网特性和改善其稳定电网的能力是风力发电技术中重要的课题[1 ,2 ,3 ] . ...
双馈风力风电机组系统接入与稳定运行仿真
1
2007
... 由于我国风力发电具有大规模、集中接入的特点,风力发电机组的电网友好性对电网安全的影响越来越显著,特别是故障穿越性能.因此,研究风力发电机组的并网特性和改善其稳定电网的能力是风力发电技术中重要的课题[1 ,2 ,3 ] . ...
双馈感应式风力发电系统低电压穿越能力研究
1
2007
... 保证风电机组在低电压穿越过程中不脱网运行是对机组的最基本要求,为改善风电机组电网友好性,机组在不脱网的同时还要发送适量的无功功率.多起电网事故后都出现了高电压的情况,就是无功补偿过量造成的.由此可见,优化风电机组在不同的故障穿越情况下的响应行为对电网故障恢复的影响至关重要[4 ,5 ,6 ] . ...
双馈电机低电压穿越时的暂态特性研究
2
2016
... 保证风电机组在低电压穿越过程中不脱网运行是对机组的最基本要求,为改善风电机组电网友好性,机组在不脱网的同时还要发送适量的无功功率.多起电网事故后都出现了高电压的情况,就是无功补偿过量造成的.由此可见,优化风电机组在不同的故障穿越情况下的响应行为对电网故障恢复的影响至关重要[4 ,5 ,6 ] . ...
... 变流器是风电机组实现低电压穿越的核心部件,由于电网电压突变很容易出现发电机定子过流、转子回路过流、直流母线过压/欠压等情况,这些现象在电网突变瞬间特别明显.如图9 所示,在电网电压跌落20%的情况下,发电机的动态模型准确反映了在低穿过程中风电机组的机电暂态和稳态特性[5 ,6 ] . ...
具有低电压穿越能力的双馈风电机组故障暂态特性分析
2
2013
... 保证风电机组在低电压穿越过程中不脱网运行是对机组的最基本要求,为改善风电机组电网友好性,机组在不脱网的同时还要发送适量的无功功率.多起电网事故后都出现了高电压的情况,就是无功补偿过量造成的.由此可见,优化风电机组在不同的故障穿越情况下的响应行为对电网故障恢复的影响至关重要[4 ,5 ,6 ] . ...
... 变流器是风电机组实现低电压穿越的核心部件,由于电网电压突变很容易出现发电机定子过流、转子回路过流、直流母线过压/欠压等情况,这些现象在电网突变瞬间特别明显.如图9 所示,在电网电压跌落20%的情况下,发电机的动态模型准确反映了在低穿过程中风电机组的机电暂态和稳态特性[5 ,6 ] . ...
具有低电压穿越能力的双馈风电机组故障暂态特性分析
2
2013
... 保证风电机组在低电压穿越过程中不脱网运行是对机组的最基本要求,为改善风电机组电网友好性,机组在不脱网的同时还要发送适量的无功功率.多起电网事故后都出现了高电压的情况,就是无功补偿过量造成的.由此可见,优化风电机组在不同的故障穿越情况下的响应行为对电网故障恢复的影响至关重要[4 ,5 ,6 ] . ...
... 变流器是风电机组实现低电压穿越的核心部件,由于电网电压突变很容易出现发电机定子过流、转子回路过流、直流母线过压/欠压等情况,这些现象在电网突变瞬间特别明显.如图9 所示,在电网电压跌落20%的情况下,发电机的动态模型准确反映了在低穿过程中风电机组的机电暂态和稳态特性[5 ,6 ] . ...
风电机组模型建立
1
2016
... 为更好地改善风机脱网问题,必须在风电机组优化低电压穿越特性的基础上,科学合理地解决无功调用问题.功率分配策略的研究非常重要,而策略研究的关键是建立准确的风机模型[7 ] . ...
风电机组模型建立
1
2016
... 为更好地改善风机脱网问题,必须在风电机组优化低电压穿越特性的基础上,科学合理地解决无功调用问题.功率分配策略的研究非常重要,而策略研究的关键是建立准确的风机模型[7 ] . ...
风电机组变速与变桨矩控制过程中的动力学问题研究
2
2007
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
... 风机机械传动部分包括5部分,即风轮、低速转轴、变速齿轮箱、高速转轴和发电机,如图2 所示[8 , 11 ] . ...
风电机组变速与变桨矩控制过程中的动力学问题研究
2
2007
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
... 风机机械传动部分包括5部分,即风轮、低速转轴、变速齿轮箱、高速转轴和发电机,如图2 所示[8 , 11 ] . ...
并网双馈风力发电机组的建模与仿真
2
2010
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
... 变流器使用矢量控制技术实现对双馈发电机的解耦控制,将实际的交流分量分解为有功分量和无功分量,并对这两个分量进行闭环控制.采用定子磁链定向矢量控制时,由定转子的磁链方程和电压方程可以得到矢量控制的原理方程[9 ] . ...
并网双馈风力发电机组的建模与仿真
2
2010
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
... 变流器使用矢量控制技术实现对双馈发电机的解耦控制,将实际的交流分量分解为有功分量和无功分量,并对这两个分量进行闭环控制.采用定子磁链定向矢量控制时,由定转子的磁链方程和电压方程可以得到矢量控制的原理方程[9 ] . ...
双馈异步风力发电机建模与仿真研究
1
2010
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
双馈异步风力发电机建模与仿真研究
1
2010
... 图1 给出了双馈型风力发电机组仿真模型的基本结构,主要包括风轮模型、传动链模型、发电机变流器模型、主控模型、变桨模型以及外部的风速模型和电网模型[8 ,9 ,10 ] . ...
2
2003
... 风机机械传动部分包括5部分,即风轮、低速转轴、变速齿轮箱、高速转轴和发电机,如图2 所示[8 , 11 ] . ...
... 由于低电压穿越持续时间较短且容易产生过电流.为保护IGBT开关不因过载而损坏,保护系统必须能够检测发电机定子、转子回路及电网侧变流器的电流、直流环节电压、电网电压、频率等,当这些量超标时,保护系统就会闭锁变流器.因此研究发电机暂态的电机模型必须能体现这些暂态量.经推导和化简,双馈异步发电机在d -q 同步旋转坐标系下的暂态数学模型[11 ,12 ] 如下所示. ...
PWM整流器及其控制策略的研究
1
2003
... 由于低电压穿越持续时间较短且容易产生过电流.为保护IGBT开关不因过载而损坏,保护系统必须能够检测发电机定子、转子回路及电网侧变流器的电流、直流环节电压、电网电压、频率等,当这些量超标时,保护系统就会闭锁变流器.因此研究发电机暂态的电机模型必须能体现这些暂态量.经推导和化简,双馈异步发电机在d -q 同步旋转坐标系下的暂态数学模型[11 ,12 ] 如下所示. ...
Study of the factors affected the rotor over-current of DFIG during the three-phase voltage dip
2008
双馈风机低电压穿越控制策略的分析与研究
1
2011
... 增加硬件电路时,可以采用增加转子侧的撬棒电路、增加直流侧的卸荷电路等方法,工程中常用的方法是在转子侧增加撬棒电路[15 ] . ...
双馈风机低电压穿越控制策略的分析与研究
1
2011
... 增加硬件电路时,可以采用增加转子侧的撬棒电路、增加直流侧的卸荷电路等方法,工程中常用的方法是在转子侧增加撬棒电路[15 ] . ...
Impacts of symmetrical and asymmetrical voltage sags on DFIG-based wind turbines considering phase-angle jump, voltage recovery,and sag parameters
1
2011
... 以某双馈型风电机组为例,按照第3节的模型研究,搭建基于Matlab软件的仿真模型,研究其在 电网故障下的风电机组运行特性[16 ,17 ] .风电机组的主要参数见表1 . ...
Control strategy of an active crowbar for DFIG based wind turbine under grid voltage dips
1
2007
... 以某双馈型风电机组为例,按照第3节的模型研究,搭建基于Matlab软件的仿真模型,研究其在 电网故障下的风电机组运行特性[16 ,17 ] .风电机组的主要参数见表1 . ...