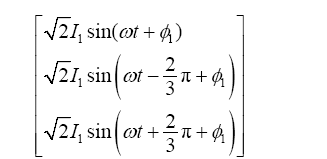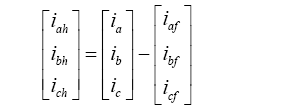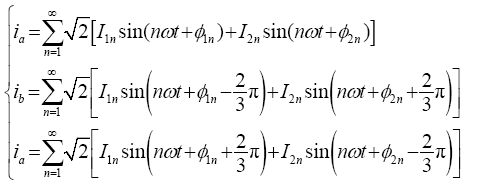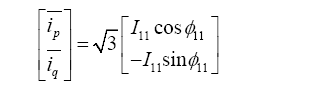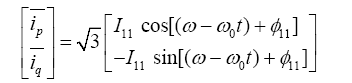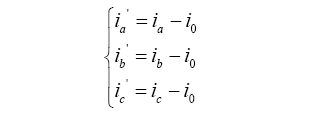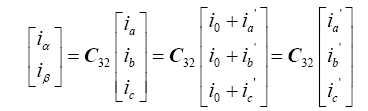1 引言
电网谐波引起的电能质量问题一直以来都是人们关注的重点,因此需要对电网谐波采取有效的抑制措施来保证电网电能质量和用电设备的可靠运行。有源滤波器可以检测出谐波电流并对其进行补偿,是解决电网谐波污染问题的一种有效方法,有源滤波器的基本原理是从电网中检测出谐波电流的含量,利用补偿装置可以产生与该谐波电流大小相等、极性相反的补偿电流,这个补偿电流与检测到的谐波电流抵消后,电网中就只含有基波电流[1 ,2 ] 。
针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性。针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进。一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路。利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性。
2 传统ip-iq检测法
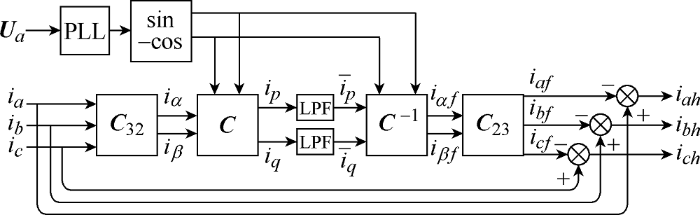
ip-iq检测法如图1 所示。其中${{U}_{a}}$为a 相电网电压,PLL(Phase locked loop)为锁相环,LPF(Low pass filter)为低通滤波器。${{\mathbf{C}}_{23}}$和${{\mathbf{C}}^{1}}$分别为矩阵${{\mathbf{C}}_{\mathbf{32}}}$和矩阵$\mathbf{C}$的逆矩阵。
(1) ${{\mathbf{C}}_{32}}=\sqrt{\frac{2}{3}}\left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\\end{matrix} \right]$
(2) $\mathbf{C}=\left[ \begin{matrix} \sin \omega t & -\cos \omega t \\ -\cos \omega t & -\sin \omega t \\\end{matrix} \right]$
图1
传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号。三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流。经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流。用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] 。
其中,三相基波电流的表达式和三相谐波电流的表达式分别为
(3)
(4)
传统的ip-iq检测法在三相对称系统中不会带来误差,但在三相不对称系统中,电压的畸变会使a相电网电压的初相角和a相正序电压的初相角之间产生相位差,造成检测结果的不准确[11 ,12 ] 。
3 改进的ip-iq检测法
3.1 基波计算误差的处理方法
在三相三线制系统中,根据对称分量法[13 ] ,将ia 、ib 、ic 表达为正序分量和负序分量之和的形式,即
(5)
式中,${{I}_{1\text{n}}}$表示第n 次正序电流有效值,${{I}_{2n}}$表示第n 次负序电流有效值,n =1时表示基波电流;${{\phi }_{1n}}$表示第n 次正序电流的初相角,${{\phi }_{2n}}$表示第n 次负序电流的初相角。根据Clark变换和瞬时无功功率理论可得
(6) $\left[ \begin{align} & {{i}_{p}} \\ & {{i}_{q}} \\ \end{align} \right]$=$\sqrt{3}\left[ \begin{align} & \sum\limits_{n=1}^{\infty }{{{I}_{1n}}\cos [(n-1)\omega t+{{\phi }_{1n}}]-{{I}_{2n}}\text{cos}[(n+1)\omega t+{{\phi }_{2n}}]} \\ & \sum\limits_{n=1}^{\infty }{-{{I}_{1n}}\sin [(n-1)\omega t+{{\phi }_{1n}}]-{{I}_{2n}}\sin [(n+1)\omega t+{{\phi }_{2n}}]} \\ \end{align} \right]$
(7)
可见$\overline{{{i}_{p}}}$、$\overline{{{i}_{q}}}$是三相电流${{i}_{a}}$、${{i}_{b}}$、${{i}_{c}}$的基波正序分量,再经过反变换可得
(8) $\left[ \begin{align} & {{i}_{a11}} \\ & {{i}_{b11}} \\ & {{i}_{c11}} \\ \end{align} \right]$=$\left[ \begin{align} & \sqrt{2}{{I}_{11}}\sin (\omega t+{{\phi }_{11}}) \\ & \sqrt{2}{{I}_{11}}\sin \left( \omega t-\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }+{{\phi }_{11}} \right) \\ & \sqrt{2}{{I}_{11}}\sin \left( \omega t+\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }+{{\phi }_{11}} \right) \\ \end{align} \right]$
式中,${{I}_{a11}}$、${{I}_{b11}}$、${{I}_{c11}}$分别表示a、b、c三相基波电流的正序分量。所以,ip-iq检测法相当于只分离出三相不对称系统的基波正序电流,而负序电流并没有被分离出来[14 ] ,导致谐波电流检测的误差。
由对称分量法可知,只要将ip-iq检测法中坐标变换矩阵${{\mathbf{C}}_{32}}$的第二列与第三列数据对调,并将反变换矩阵${{\mathbf{C}}_{23}}$的第二行与第三行数据对调,即可检测出基波负序分量[15 ] 。
3.2 相位计算误差的处理方法
由于锁相环在实际应用中极易受到信号的干扰,会引起相位计算误差,从而导致谐波电流检测误差。考虑利用与电网电压同相位的正、余弦信号代替锁相环,消除锁相环对波形畸变的影响[16 ] 。方法的可行性分析如下。
设矩阵${{\mathbf{C}}_{0}}$的恒定角频率为${{\omega }_{0}}$,则
(9) ${{\mathbf{C}}_{0}}=\left[ \begin{matrix} \sin {{\omega }_{0}}t & -\cos {{\omega }_{0}}t \\ -\cos {{\omega }_{0}}t & -\sin {{\omega }_{0}}t \\\end{matrix} \right]$
则瞬时有功电流${{i}_{p}}$和瞬时无功电流${{i}_{q}}$为
(10) $\left[ \begin{align} & {{i}_{p}} \\ & {{i}_{q}} \\ \end{align} \right]={{C}_{0}}{{C}_{32}}\sqrt{3}\times$$\left[ \begin{align} & \sum\limits_{n=1}^{\infty }{{{I}_{1n}}\text{cos}[(n\omega -{{\omega }_{0}})t+{{\phi }_{1n}}]-{{I}_{2n}}\text{cos}[(n\omega +{{\omega }_{0}})t+{{\phi }_{2n}}]} \\ & \sum\limits_{n=1}^{\infty }{-{{I}_{1n}}\sin [(n\omega -{{\omega }_{0}})t+{{\phi }_{1n}}]-{{I}_{2n}}\sin [(n\omega +{{\omega }_{0}})t+{{\phi }_{2n}}]} \\ \end{align} \right]$
根据国家《电能质量电力系统允许偏差的规定》,电力系统的正常允许偏差值不会超过0.5 Hz。低通滤波器在使用时通常会预先设定一个较低的截止频率,高于截止频率的交流分量会被滤除[17 ] 。所以ip 和iq 在经过低通滤波器滤波后可以分离出二者的直流分量$\overline{{{i}_{p}}}$、$\overline{{{i}_{q}}}$,即
(11)
(12) $\left[ \begin{align} & {{i}_{a1f}} \\ & {{i}_{b1f}} \\ & {{i}_{c1f}} \\ \end{align} \right]$=$\left[ \begin{align} & \sqrt{2}{{I}_{11}}\sin (\omega t+{{\phi }_{11}}) \\ & \sqrt{2}{{I}_{11}}\sin \left( \omega t-\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }+{{\phi }_{11}} \right) \\ & \sqrt{2}{{I}_{11}}\sin \left( \omega t+\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }+{{\phi }_{11}} \right) \\ \end{align} \right]$
对比式(12)与式(8)的结果完全相同,这说明利用与电网电压同相位的正、余弦信号代替锁相环,不会影响最终的检测结果[18 ] 。
3.3 一种适用于三相三线、三相四线制电路的通用型方法
在三相四线制系统中,中性线的存在会产生零序分量,使得ip-iq检测法不能应用于三相四线制不对称系统。因此考虑在进行Clark变换之前先从总电流中分离出零序分量,再进行后续的坐标变换[19 ,20 ] 。算法的推导过程如下。
根据对称分量法可知零序分量${{i}_{0}}$的表达式为
(13) ${{i}_{0}}={\left( {{i}_{a}}+{{i}_{b}}+{{i}_{c}} \right)}/{3}\$;
(14)
(15)
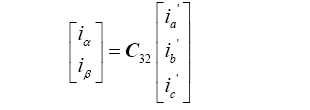
(16)
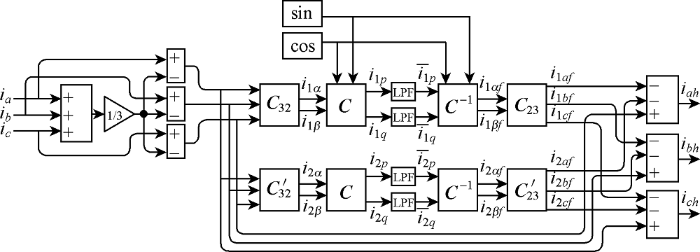
对比式(15)与式(16)可知,在三相四线制系统中,先分离出零序电流,再进行Clark变换,不会对使用ip-iq检测法检测谐波产生影响。所以可以通过增加零序电流分离模块使ip-iq检测法直接运用于三相四线制系统。
图2
4 建模与仿真分析
4.1 建模与仿真参数设置
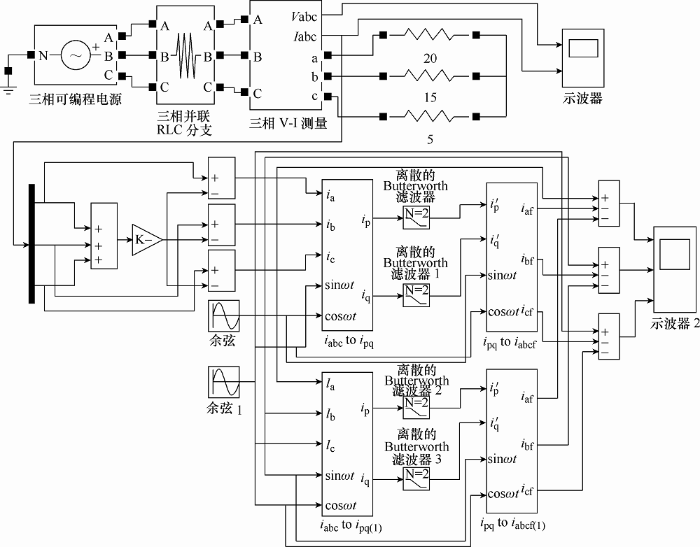
根据图1 和图2 分别搭建传统的ip-iq检测法和改进的ip-iq检测法的仿真模型,针对不对称系统和对称系统分别进行仿真。在三相可编程电压源中添加三次谐波,设置谐波幅值为$\text{0}\text{.2}\times 220\sqrt{2}$V,初相角为-120°,在仿真开始的0.1~0.2 s时段添加谐波。改进的ip-iq检测法仿真模型如图3 所示。
图3
4.2 传统的ip-iq检测法
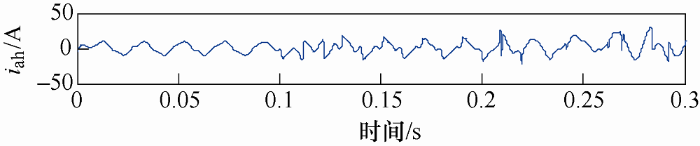
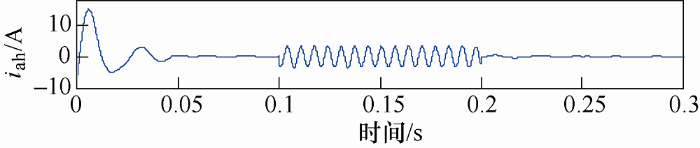
传统的ip-iq检测法检测得到的a相谐波电流如图4 所示。理想情况下,当电路中加入三次谐波时,检测到的谐波电流应为频率为150 Hz的正弦波。但在实际情况下,加入谐波的0.1~0.2 s之间,谐波电流并非正弦波,不符合理想状况。
图4
4.3 改进的ip-iq检测法
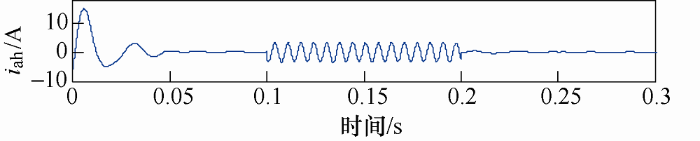
利用改进的ip-iq检测法检测到的a相谐波电流如图5 所示。在加入谐波的0.1~0.2 s之间,共有15个周波,可计算出谐波的频率为150 Hz,同时撤去谐波后,检测的谐波电流恢复为零值,与理想状况相符合。
图5
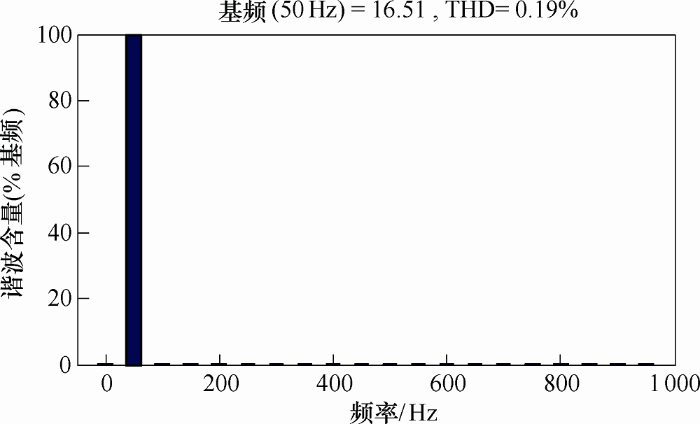
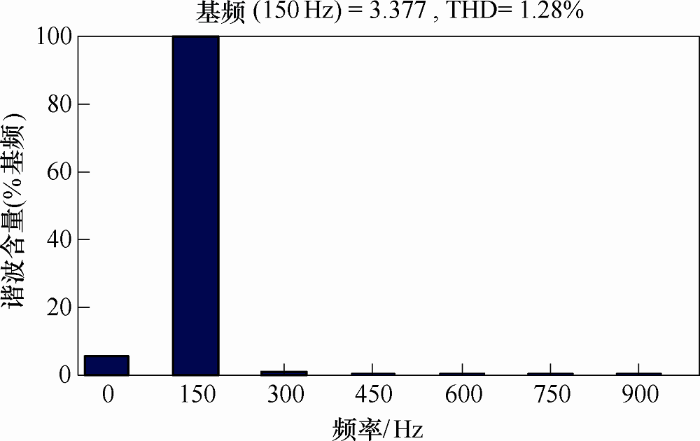
取a相基波电流和谐波电流进行傅里叶分析。a相基波电流的有效值为16.51 A,畸变率THD为0.19%。a相谐波电流的有效值为3.377 A,畸变率THD为1.28%。傅里叶分析的结果说明,在误差允许的范围内,改进的ip-iq检测法可以正确且有效地检测出三相三线制不对称系统的谐波电流。a相基波电流和谐波电流傅里叶分析结果如图6 和图7 所示。
图6
图7
同理,在三相四线制不对称系统中检测到的a相谐波电流如图8 所示。
图8
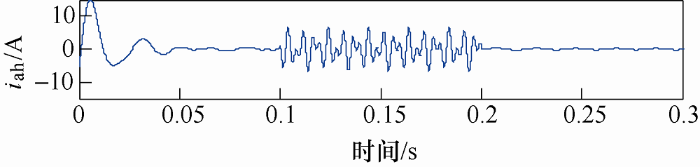
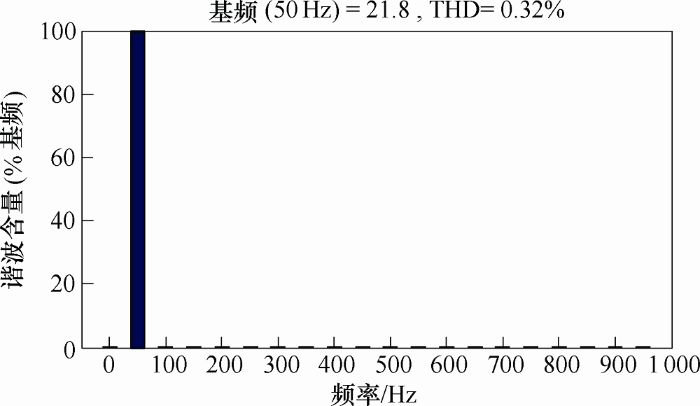
取a相基波电流和谐波电流进行傅里叶分析。a相基波电流的有效值为21.76 A,畸变率THD为0.34%。a相谐波电流的有效值为4.477 A,畸变率THD为1.98%。同时,为说明该方法的合理性,在仿真开始的0.1~0.2 s加入三次和五次谐波,理想情况下检测到的a相基波电流频率应为50 Hz。叠加三次和五次谐波后,检测到的a相谐波电流波形如图9 所示,a相基波电流傅里叶分析结果如图10 所示。
图9
图10
叠加三次和五次谐波后,a相基波电流的有效值为21.8 A,畸变率THD为0.32%。相较于传统的ip-iq检测法,明显降低了检测误差,说明改进的ip-iq检测法可以正确且有效地检测出三相四线制不对称系统的谐波电流。
经过仿真分析,该改进方法同样适用于三相对称系统。改进前后的ip-iq检测法效果对比见表1 。
5 结论
传统的ip-iq检测法在不对称系统的谐波电流检测中存在大量误差,这些误差来源于负序分量的存在以及相位计算的不准确。针对传统方法的不足,本文提出了一种通用型谐波电流检测方法:通过对称分量法建立负序电流分离模块,提高基波电流检测精度;通过设定与电网电压相等的频率代替ip-iq检测法坐标变换矩阵中的频率,解决了锁相环带来的相位计算不准问题;通过增加零序电流分离模块,实现对三相三线制和三相四线制不对称系统的通用性。同时,这种改进方法也适用于对称系统。本文利用Matlab/Simulink进行建模、仿真和验证,证明了改进的ip-iq检测法的正确性和可行性。
参考文献
View Option
[1]
田志丹 , 李友才 , 陆荃 . 基于广义谐波理论的电能质量扰动检测方法
[J]. 水电站机电技术 , 2018 ,41 (5 ):19 -22,105 .
[本文引用: 1]
Tian Zhidan Li Youcai Lu Quan . A power quality disturbance detection method based on generalized harmonic theory
[J]. Mechanical & Electrical Technique of Hydropower Station , 2018 ,41 (5 ):19 -22,105 .
[本文引用: 1]
[2]
佟祉璇 . 电力系统谐波检测方法的分析与研究
[D]. 锦州:辽宁工业大学 , 2017 .
[本文引用: 1]
[3]
杨怀仁 . 基于瞬时无功功率理论的三相谐波电流检测研究
[D]. 杭州:浙江大学 , 2014 .
[本文引用: 1]
[4]
郑征 , 杜翠静 , 常万仓 . 三相不对称系统中谐波电流检测的新方法
[J]. 电力系统及其自动化学报 , 2010 ,22 (3 ):50 -54 .
[本文引用: 1]
Zheng Zheng Du Cuijing Chang Wancang . A new method for harmonic current detection in three-phase asymmetric system
[J]. Proceedings of the CSU-EPSA , 2010 ,22 (3 ):50 -54 .
[本文引用: 1]
[5]
万钧力 , 刘浩 , 黄曌 . 基于组合运算的不平衡电网谐波检测方法
[J]. 电气应用 , 2018 ,37 (3 ):54 -57,89 .
[本文引用: 1]
Wan Junli Liu Hao Huang Zhao . Harmonic detection method for unbalanced power grid based on combination operation
[J]. Electrotechnical Application , 2018 ,37 (3 ):54 -57,89 .
[本文引用: 1]
[6]
周林 , 栗秋华 , 张凤 . 基于ip-iq法的三相四线制系统任意次谐波电流的检测新方法
C]//2006年中国电机工程学会年会论文集. 重庆大学 , 2006 .
[本文引用: 1]
Zhou Lin Li Qiuhua Zhang Feng . A new method for detecting arbitrary harmonic currents in three-phase four-wire system based on ip-iq method
C]// Proceedings of the 2006 Annual Meeting of China Electrical Engineering Society. Chongqing University , 2006 .
[本文引用: 1]
[7]
易桂平 , 胡仁杰 . 基于瞬时无功功率理论的谐波电流检测法研究
[J]. 电力与能源 , 2014 ,35 (5 ):566 -571,575 .
[本文引用: 1]
Yi Guiping Hu Renjie . Research on harmonic current detection method based on instantaneous reactive power theory
[J]. Power and Energy , 2014 ,35 (5 ):566 -571,575 .
[本文引用: 1]
[8]
叶明佳 . 基于瞬时无功功率理论的谐波和无功电流检测方法研究
[D]. 重庆:重庆大学 , 2012 .
[本文引用: 1]
[9]
唐蕾 , 陈维荣 . 瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析
[J]. 电网技术 , 2008 (5 ):66 -69,86 .
[本文引用: 1]
Tang Lei Chen Weirong . Derivation of theoretical coordinate transformation of instantaneous reactive power and analysis of principle of harmonic current detection
[J]. Power System Technology , 2008 (5 ):66 -69,86 .
[本文引用: 1]
[10]
Liu Hongchun Sun Shuguang Wang Jingqin , et al . Study ip-iq theory and wavelet transform method for harmonic current detection. International Conference on Automatic Control and
Artificial Intelligence. 2012 .
[本文引用: 1]
[11]
吾布里•阿依丁 , 郭辉 . 三相电压不对称时谐波电流检测方法
[J]. 煤矿机电 , 2008 (3 ):81 -83,86 .
[本文引用: 1]
Wubri Ayiding Guo Hui . Harmonic current detection method for three-phase voltage asymmetry
[J]. Colliery Mechanical and Electrical Technology , 2008 (3 ):81 -83,86 .
[本文引用: 1]
[12]
王志达 . 基于瞬时无功功率理论的电力系统谐波检测分析
[D]. 北京:华北电力大学 , 2015 .
[本文引用: 1]
[13]
王丽萍 . 三相不对称电路的对称分量法
[J]. 铜陵财经专科校报 , 2002 (2 ):77 -79 .
[本文引用: 1]
Wang Liping . Symmetric component method for three-phase asymmetric circuit
[J]. Tongling College of Finance and Economics , 2002 (2 ):77 -79 .
[本文引用: 1]
[14]
艾永乐 , 许增渊 , 李向前 , 等 . 基于i_p-i_q改进的谐波和有功电流检测研究
[J]. 电子测量与仪器学报 , 2018 ,32 (2 ):172 -178 .
[本文引用: 1]
Ai Yongle Xu Zengyuan Li Xiangqian , et al . Study on harmonic and active current detection based on improved i_p-i_q
[J]. Journal of Electronic Measurement and Instrument , 2018 ,32 (2 ):172 -178 .
[本文引用: 1]
[15]
李萌 . 基于电网不平衡的谐波检测改进算法研究
[J]. 控制工程 , 2018 ,25 (4 ):607 -613 .
[本文引用: 1]
Li Meng . Research on improved algorithm of harmonic detection based on power network unbalance
[J]. Control Engineering of China , 2018 ,25 (4 ):607 -613 .
[本文引用: 1]
[16]
刘继权 , 张茂松 . 基于瞬时无功功率理论的新型谐波检测法
[J]. 电测与仪表 , 2012 ,49 (10 ):29 -32,51 .
[本文引用: 1]
Liu Jiquan Zhang Maosong . A new harmonic detection method based on instantaneous reactive power theory
[J]. Electrical Measurement & Instrumentation , 2012 ,49 (10 ):29 -32,51 .
[本文引用: 1]
[17]
许德志 , 刘跃 , 杨勇 . 一种改进型i_p-i_q三相畸变电流检测法的仿真研究
[J]. 电测与仪表 , 2005 (11 ):5 -8 .
[本文引用: 1]
Xu Dezhi Liu Yue Yang Yong . Simulation of an improved i_p-i_q three-phase distortion current detection method
[J]. Electrical Measurement & Instrumentation , 2005 (11 ):5 -8 .
[本文引用: 1]
[18]
周林 , 张凤 , 栗秋华 , 等 . 无锁相环i_p-i_q检测任意次谐波电流的新方法
[J]. 高电压技术 , 2007 (7 ):129 -133 .
[本文引用: 1]
Zhou Lin Zhang Feng Li Qiuhua , et al . A new method for detecting any harmonic current without phase-locked loop i_p-i_q
[J]. High Voltage Engineering , 2007 (7 ):129 -133 .
[本文引用: 1]
[19]
亓建英 , 邹黎 , 李超 , 等 . 三相四线制电网谐波电流检测ip-iq法的改进
[J]. 山东理工大学学报(自然科学版) , 2013 ,27 (6 ):63 -67 .
[本文引用: 1]
Qi Jianying Zou Li Li Chao , et al . Improvement of ip-iq method for harmonic current detection in three-phase four-wire power grid
[J]. Journal of Shandong University of Technology(Natural Science) , 2013 ,27 (6 ):63 -67 .
[本文引用: 1]
[20]
武海霖 . 三相四线制低压配电网谐波和瞬时无功电流检测方法的改进
[D]. 沈阳:沈阳农业大学 , 2017 .
[本文引用: 1]
[21]
Marcu M Popescu F G Niculescu T et al . Simulation of power active filter using instantaneous reactive power theory
[C]// Harmonics and Quality of Power (ICHQP),2014 IEEE 16th International Conference on , 2014 .
基于广义谐波理论的电能质量扰动检测方法
1
2018
... 电网谐波引起的电能质量问题一直以来都是人们关注的重点,因此需要对电网谐波采取有效的抑制措施来保证电网电能质量和用电设备的可靠运行.有源滤波器可以检测出谐波电流并对其进行补偿,是解决电网谐波污染问题的一种有效方法,有源滤波器的基本原理是从电网中检测出谐波电流的含量,利用补偿装置可以产生与该谐波电流大小相等、极性相反的补偿电流,这个补偿电流与检测到的谐波电流抵消后,电网中就只含有基波电流[1 ,2 ] . ...
基于广义谐波理论的电能质量扰动检测方法
1
2018
... 电网谐波引起的电能质量问题一直以来都是人们关注的重点,因此需要对电网谐波采取有效的抑制措施来保证电网电能质量和用电设备的可靠运行.有源滤波器可以检测出谐波电流并对其进行补偿,是解决电网谐波污染问题的一种有效方法,有源滤波器的基本原理是从电网中检测出谐波电流的含量,利用补偿装置可以产生与该谐波电流大小相等、极性相反的补偿电流,这个补偿电流与检测到的谐波电流抵消后,电网中就只含有基波电流[1 ,2 ] . ...
电力系统谐波检测方法的分析与研究
1
2017
... 电网谐波引起的电能质量问题一直以来都是人们关注的重点,因此需要对电网谐波采取有效的抑制措施来保证电网电能质量和用电设备的可靠运行.有源滤波器可以检测出谐波电流并对其进行补偿,是解决电网谐波污染问题的一种有效方法,有源滤波器的基本原理是从电网中检测出谐波电流的含量,利用补偿装置可以产生与该谐波电流大小相等、极性相反的补偿电流,这个补偿电流与检测到的谐波电流抵消后,电网中就只含有基波电流[1 ,2 ] . ...
基于瞬时无功功率理论的三相谐波电流检测研究
1
2014
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
三相不对称系统中谐波电流检测的新方法
1
2010
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
三相不对称系统中谐波电流检测的新方法
1
2010
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
基于组合运算的不平衡电网谐波检测方法
1
2018
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
基于组合运算的不平衡电网谐波检测方法
1
2018
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
基于ip-iq法的三相四线制系统任意次谐波电流的检测新方法
1
2006
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
基于ip-iq法的三相四线制系统任意次谐波电流的检测新方法
1
2006
... 针对传统ip-iq检测法,文献[3 ]中指出传统ip-iq检测法在谐波电流检测中存在的问题,但未进行改进;文献[4 ]中通过建立新的数学模型和改进算法实现在电网不平衡状态下检测谐波电流,但该方法计算量大且改进后谐波电流的畸变率仍较大;文献[5 ]中的改进方法比传统的ip-iq检测法能够更快速、更准确地检测出电网负序电流、谐波电流等,且明显降低了基波电流的畸变率,但并未考虑如何将该改进法应用于三相四线制电路;文献[6 ]利用等价三角变换实现了三相四线制系统任意次谐波电流的检测,但并未验证其是否具有通用性.针对上述提出的问题,本文在ip-iq检测法的基础上进行三处改进.一是增加负序电流分离模块,减小基波计算误差;二是去除锁相环,消除相位计算不准问题;三是增加零序电流分离模块,使其同时适用于三相三线制和三相四线制电路.利用Matlab/Simulink仿真软件验证了该改进方法的正确性与可行性. ...
基于瞬时无功功率理论的谐波电流检测法研究
1
2014
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
基于瞬时无功功率理论的谐波电流检测法研究
1
2014
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
基于瞬时无功功率理论的谐波和无功电流检测方法研究
1
2012
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析
1
2008
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析
1
2008
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
Study ip-iq theory and wavelet transform method for harmonic current detection. International Conference on Automatic Control and
1
2012
... 传统的ip-iq检测法通过锁相环和正、余弦信号发生电路得到与a相电网电压${{V}_{a}}$同相位的正、余弦信号.三相电流经过Clark变换得到α、β 相的电流,利用瞬时无功功率的定义可得到瞬时有功电流和瞬时无功电流.经过低通滤波器得到二者的直流分量后,再经过两次反变换可得到三相基波电流.用三相电流减去三相基波电流可得到三相谐波电流[7 ,8 ,9 ,10 ] . ...
三相电压不对称时谐波电流检测方法
1
2008
... 传统的ip-iq检测法在三相对称系统中不会带来误差,但在三相不对称系统中,电压的畸变会使a相电网电压的初相角和a相正序电压的初相角之间产生相位差,造成检测结果的不准确[11 ,12 ] . ...
三相电压不对称时谐波电流检测方法
1
2008
... 传统的ip-iq检测法在三相对称系统中不会带来误差,但在三相不对称系统中,电压的畸变会使a相电网电压的初相角和a相正序电压的初相角之间产生相位差,造成检测结果的不准确[11 ,12 ] . ...
基于瞬时无功功率理论的电力系统谐波检测分析
1
2015
... 传统的ip-iq检测法在三相对称系统中不会带来误差,但在三相不对称系统中,电压的畸变会使a相电网电压的初相角和a相正序电压的初相角之间产生相位差,造成检测结果的不准确[11 ,12 ] . ...
三相不对称电路的对称分量法
1
2002
... 在三相三线制系统中,根据对称分量法[13 ] ,将ia 、ib 、ic 表达为正序分量和负序分量之和的形式,即 ...
三相不对称电路的对称分量法
1
2002
... 在三相三线制系统中,根据对称分量法[13 ] ,将ia 、ib 、ic 表达为正序分量和负序分量之和的形式,即 ...
基于i_p-i_q改进的谐波和有功电流检测研究
1
2018
... 式中,${{I}_{a11}}$、${{I}_{b11}}$、${{I}_{c11}}$分别表示a、b、c三相基波电流的正序分量.所以,ip-iq检测法相当于只分离出三相不对称系统的基波正序电流,而负序电流并没有被分离出来[14 ] ,导致谐波电流检测的误差. ...
基于i_p-i_q改进的谐波和有功电流检测研究
1
2018
... 式中,${{I}_{a11}}$、${{I}_{b11}}$、${{I}_{c11}}$分别表示a、b、c三相基波电流的正序分量.所以,ip-iq检测法相当于只分离出三相不对称系统的基波正序电流,而负序电流并没有被分离出来[14 ] ,导致谐波电流检测的误差. ...
基于电网不平衡的谐波检测改进算法研究
1
2018
... 由对称分量法可知,只要将ip-iq检测法中坐标变换矩阵${{\mathbf{C}}_{32}}$的第二列与第三列数据对调,并将反变换矩阵${{\mathbf{C}}_{23}}$的第二行与第三行数据对调,即可检测出基波负序分量[15 ] . ...
基于电网不平衡的谐波检测改进算法研究
1
2018
... 由对称分量法可知,只要将ip-iq检测法中坐标变换矩阵${{\mathbf{C}}_{32}}$的第二列与第三列数据对调,并将反变换矩阵${{\mathbf{C}}_{23}}$的第二行与第三行数据对调,即可检测出基波负序分量[15 ] . ...
基于瞬时无功功率理论的新型谐波检测法
1
2012
... 由于锁相环在实际应用中极易受到信号的干扰,会引起相位计算误差,从而导致谐波电流检测误差.考虑利用与电网电压同相位的正、余弦信号代替锁相环,消除锁相环对波形畸变的影响[16 ] .方法的可行性分析如下. ...
基于瞬时无功功率理论的新型谐波检测法
1
2012
... 由于锁相环在实际应用中极易受到信号的干扰,会引起相位计算误差,从而导致谐波电流检测误差.考虑利用与电网电压同相位的正、余弦信号代替锁相环,消除锁相环对波形畸变的影响[16 ] .方法的可行性分析如下. ...
一种改进型i_p-i_q三相畸变电流检测法的仿真研究
1
2005
... 根据国家《电能质量电力系统允许偏差的规定》,电力系统的正常允许偏差值不会超过0.5 Hz.低通滤波器在使用时通常会预先设定一个较低的截止频率,高于截止频率的交流分量会被滤除[17 ] .所以ip 和iq 在经过低通滤波器滤波后可以分离出二者的直流分量$\overline{{{i}_{p}}}$、$\overline{{{i}_{q}}}$,即 ...
一种改进型i_p-i_q三相畸变电流检测法的仿真研究
1
2005
... 根据国家《电能质量电力系统允许偏差的规定》,电力系统的正常允许偏差值不会超过0.5 Hz.低通滤波器在使用时通常会预先设定一个较低的截止频率,高于截止频率的交流分量会被滤除[17 ] .所以ip 和iq 在经过低通滤波器滤波后可以分离出二者的直流分量$\overline{{{i}_{p}}}$、$\overline{{{i}_{q}}}$,即 ...
无锁相环i_p-i_q检测任意次谐波电流的新方法
1
2007
... 对比式(12)与式(8)的结果完全相同,这说明利用与电网电压同相位的正、余弦信号代替锁相环,不会影响最终的检测结果[18 ] . ...
无锁相环i_p-i_q检测任意次谐波电流的新方法
1
2007
... 对比式(12)与式(8)的结果完全相同,这说明利用与电网电压同相位的正、余弦信号代替锁相环,不会影响最终的检测结果[18 ] . ...
三相四线制电网谐波电流检测ip-iq法的改进
1
2013
... 在三相四线制系统中,中性线的存在会产生零序分量,使得ip-iq检测法不能应用于三相四线制不对称系统.因此考虑在进行Clark变换之前先从总电流中分离出零序分量,再进行后续的坐标变换[19 ,20 ] .算法的推导过程如下. ...
三相四线制电网谐波电流检测ip-iq法的改进
1
2013
... 在三相四线制系统中,中性线的存在会产生零序分量,使得ip-iq检测法不能应用于三相四线制不对称系统.因此考虑在进行Clark变换之前先从总电流中分离出零序分量,再进行后续的坐标变换[19 ,20 ] .算法的推导过程如下. ...
三相四线制低压配电网谐波和瞬时无功电流检测方法的改进
1
2017
... 在三相四线制系统中,中性线的存在会产生零序分量,使得ip-iq检测法不能应用于三相四线制不对称系统.因此考虑在进行Clark变换之前先从总电流中分离出零序分量,再进行后续的坐标变换[19 ,20 ] .算法的推导过程如下. ...
Simulation of power active filter using instantaneous reactive power theory
2014