1 引言
在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现。多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径。多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波。这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] 。但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平。移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波。对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用。传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题。为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的。通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小。此外,串并联多个直线式移相变压器可以得到高电压、大电流。本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析。
2 直线式移相变压器逆变系统的原理与结构
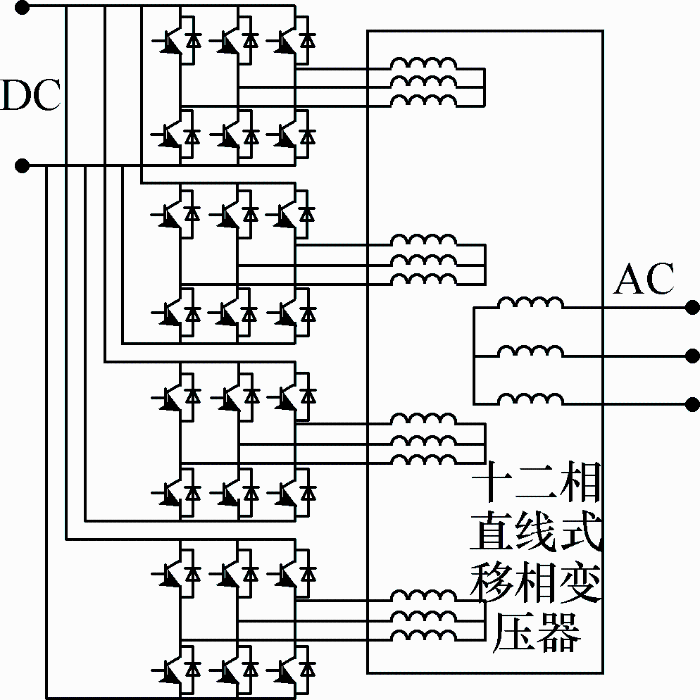
目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作。为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] 。本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示。
图1
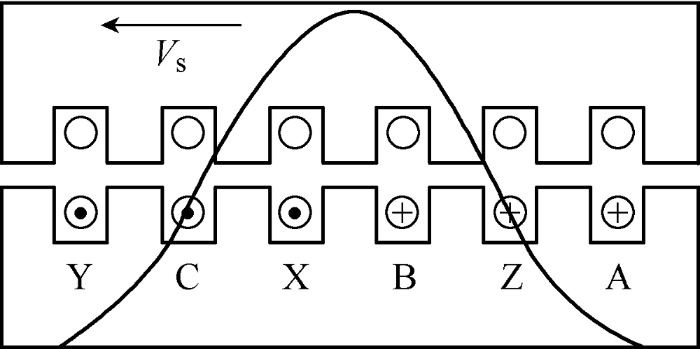
通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小。此外,串并联多个直线式移相变压器可以得到高电压、大电流。类似于直线电动机的工作原理,直线式移相变压器的原边通以三相交流电(在此设计中是四组三相六阶梯波合成三相24阶梯波近似三相交流正弦波)当三相电流随着时间变化时,气隙磁场即行波磁场,按A、B、C的相序沿直线移动,如图2 所示。行波磁场的速度${{V}_{\text{s}}}=2f\tau \left( \text{m}/\text{s} \right)$。行波磁场切割副边线圈产生感应电动势,副边线圈输出三相交流电。由于原边副边都是固定不动的,转差率$s=\frac{{{V}_{\text{s}}}-V}{{{V}_{\text{s}}}}=\frac{{{V}_{\text{s}}}-0}{{{V}_{\text{s}}}}=1$,
图2
3 直线式移相变压器逆变系统的数学模型
3.1 直线式移相变压器的电压方程
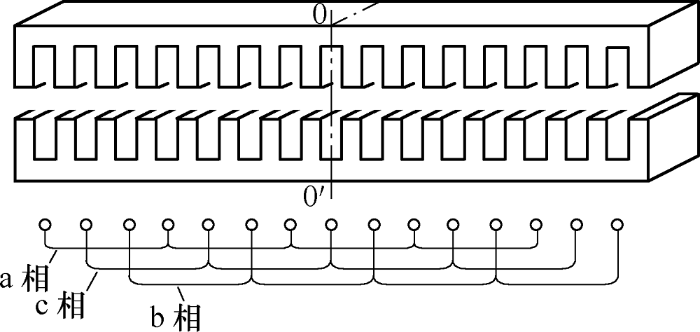
直线式移相变压器的绕组分布如图3 所示,初级绕组为变压器的原边,次级绕组为变压器的副边。
图3
(1) ${{\dot{U}}_{S}}=R{{\dot{I}}_{S}}+\frac{\text{d}{{\varphi }_{s}}}{\text{d}t}$
(2) ${{\psi }_{_{S}}}={{L}_{SS}}+{{L}_{Sr}}{{I}_{T}}$
${{^{{{{\dot{U}}}_{S}}=\text{ }\!\!\{\!\!\text{ }{{{\dot{U}}}_{S1}}\ {{{\dot{U}}}_{S2}}\cdots {{{\dot{U}}}_{S12}}\}}}^{^{\overset{\text{T}}{\mathop{{}}}\,}}}$
${{R}_{S}}=\text{diag}{{[{{r}_{s}}{{r}_{s}}\cdots \ \ {{r}_{s}}]}^{\text{T}}}$
${{I}_{S}}={{\{{{I}_{S1}}{{I}_{S2}}\ldots {{I}_{S12}}\}}^{\text{T}}}$
${{L}_{SS}}=\left( \begin{matrix} {{L}_{SS.1}} & {{L}_{SS.12}} \\ {{L}_{SS12.1}} & {{L}_{SS12.12}} \\\end{matrix} \right)$
${{L}_{sr}}=\left( \begin{matrix} {{L}_{sr1.1}} & {{L}_{sr1.2}} & {{L}_{sr1.3}} \\ \vdots & \vdots & \vdots \\ {{L}_{sr2.1}} & {{L}_{sr2.2}} & {{L}_{sr2.3}} \\\end{matrix} \right)$
${{I}_{r}}={{[{{I}_{r1}}{{I}_{r2}}{{I}_{r3}}]}^{\text{T}}}$
式中 ${{\dot{U}}_{S}}$——初级侧输入电压矢量;
${{\psi }_{_{S}}}$——直线式移相变压器初级侧磁链矩阵;
由于直线式移相变压器初级侧与次级侧是固定的,因此初级侧与次级侧之间的电感矩阵不随时间变化。将磁链表达式(2)代入原边绕组的电压方程式(1)可得
(3) $\dot{U}S=RS\dot{I}S+LSS\frac{\text{d}{{i}_{s}}}{\text{d}t}+LSr\frac{\text{d}{{i}_{r}}}{\text{d}t}$
直线式移相变压器的次级侧三相绕组接三相对称负载,每相负载阻抗${{Z}_{\text{L}}}={{r}_{\text{L}}}+\text{j}\omega {{l}_{L}}$,次级侧输出电压方程为
(4) $\dot{U}r=(Rr+Rl)\dot{I}r+Ll\frac{\text{d}{{i}_{r}}}{\text{d}t}+\frac{\text{d}\psi r}{\text{d}t}$
(5) $\dot{\psi }r=Lrr\dot{I}r+Lrs\dot{I}s$
${{R}_{T}}=\text{diag}[{{r}_{r}}{{r}_{r}}{{r}_{r}}]$
${{R}_{l}}=\text{diag}[{{r}_{l}}{{r}_{l}}{{r}_{l}}]$
${{L}_{l}}=\text{diag}[{{L}_{l}}{{L}_{l}}{{L}_{l}}]$
${{L}_{rr}}=\left( \begin{matrix} {{L}_{rr1.1}} & {{L}_{rr1.2}} & {{L}_{rr1.3}} \\ {{L}_{rr2.1}} & {{L}_{rr2.2}} & {{L}_{rr2.3}} \\ {{L}_{rr3.1}} & {{L}_{rr3.2}} & {{L}_{rr3.3}} \\\end{matrix} \right)$
式中 ${{R}_{T}}$——次级侧绕组电阻矩阵;
${{\psi }_{r}}$——直线式移相变压器次级侧磁链矩阵;
${{L}_{rs}}$——次级侧和初级侧互感矩阵,$Lrs={{L}^{T}}sr$。
将磁链表达式(5)代入次级侧绕组的电压方程式(4)可得
(6) ${{\dot{U}}_{r}}=({{R}_{L}}+{{R}_{T}}){{\dot{I}}_{r}}+({{L}_{l}}+{{L}_{rr}})\frac{\text{d}ir}{\text{d}t}+{{L}_{rs}}\frac{\text{d}ir}{\text{d}t}$
将初级侧绕组的电压方程(3)和次级侧绕组的电压方程(6)写在一起,可得完整的电压方程如下
(7) $\dot{U}={{L}_{T}}\frac{dI}{dt}+{{R}_{T}}\dot{I}$
$\dot{U}={{({{\dot{U}}_{S}}0)}^{\text{T}}}$
${{L}_{T}}=\left( \begin{matrix} {{L}_{ss}} & {{L}_{sr}} \\ {{L}_{rs}} & {{L}_{ss}}\text{+}{{L}_{l}} \\\end{matrix} \right)$
$\dot{I}={{({{\dot{I}}_{S}}{{\dot{I}}_{T}})}^{\text{T}}}$
${{R}_{T}}=\left( \begin{matrix} {{R}_{S}} & 0 \\ 0 & {{R}_{L}}+{{R}_{T}} \\\end{matrix} \right)$
式中 $\dot{U}$——直线式移相变压器的电压矢量;
3.2 电感参数的计算
通过绕组函数分析方法来计算本模型中各绕组的自感及互感参数[16 ,17 ] ,初级侧12相整距绕组中,第i 相的自感为
(8) $Li.i=\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{Ni(\varphi )}\times Ni(\varphi )\text{d}\varphi$ =$\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\times \frac{\text{ }\!\!\pi\!\!\text{ }}{2}{{N}^{2}}=Lsm$
式中,${{\mu }_{0}}$为真空磁导率;${{g}_{0}}$为气隙长度;r 为气隙圆周半径;l 为铁心有效长度;N 为初级侧单相绕组的串联匝数。设初级侧12相整距绕组中任意2个绕组a,b相距的电角度为$\theta$,当$\theta <\pi $时,绕组a,b互感为
(9) $Lab=\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{Na(\varphi )}\times Nb(\varphi )\text{d}\varphi$ =$\frac{{{\mu }_{0}}rl\text{ }\!\!\pi\!\!\text{ }{{N}^{2}}}{2{{g}_{0}}}\times \left( 1-\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\theta \right)=Lsm\left( 1-\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\theta \right)$
(10) $Lab=Lsm\left[ -1+\frac{2}{\text{ }\!\!\pi\!\!\text{ }}(\theta -\text{ }\!\!\pi\!\!\text{ }) \right]$
根据上述分析过程,可写出初级侧12相整距绕组的电感矩阵
(11) ${{L}_{SS}}={{L}_{Sm}}\left[ \begin{matrix} 1 & \frac{2}{3} & \frac{1}{3} & 0 & \cdots & \frac{2}{3} \\ \frac{2}{3} & 1 & \frac{2}{3} & \frac{1}{3} & \cdots & \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} & 1 & \frac{2}{3} & \cdots & 0 \\ 0 & \frac{1}{3} & \frac{2}{3} & 1 & \cdots & -\frac{1}{3} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{2}{3} & \frac{1}{3} & 0 & -\frac{1}{3} & \cdots & 1 \\\end{matrix} \right]+{{L}_{\text{S }\!\!\sigma\!\!\text{ }}}{{I}_{12\times 12}}$
式中,${{L}_{\text{S }\!\!\sigma\!\!\text{ }}}$为初级侧漏感;${{I}_{12\times 12}}$为单位阵。
次级侧的三相绕组采用分布结构,同时采用短距和长距绕组结合使用以消除三相不对称所带来的影响。
(12) ${{L}_{A.A}}={{L}_{B.B}}={{L}_{C.C}}=\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{NA(\varphi })\times NA(\varphi )\text{d}\varphi$ =$\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\cdot \frac{4}{\text{ }\!\!\pi\!\!\text{ }}N{{r}^{2}}=Lrm$
(13) ${{L}_{A.B}}=\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{NA(\varphi )}\times NB(\varphi )\text{d}\varphi $=$\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\cdot \frac{4}{\text{ }\!\!\pi\!\!\text{ }}N{{r}^{2}}\cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3}$
式中,$Nr$为次级侧绕组每相的等效串联匝数,其数值等于实际串联匝数与绕组系数之积。
(14) ${{L}_{rr}}={{L}_{rm}}\left( \begin{matrix} 1 & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & \cos \frac{4\text{ }\!\!\pi\!\!\text{ }}{3} \\ \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & 1 & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} \\ \cos \frac{4\text{ }\!\!\pi\!\!\text{ }}{3} & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & 1 \\\end{matrix} \right)$
这里我们假设初级侧a1 相绕组与次级侧A相绕组的轴线重合,那么它们的互感为
(15) ${{L}_{Sr1.1}}=\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\int_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{NA(\varphi )}\times Na1(\varphi )\text{d}\varphi$ =$\frac{{{\mu }_{0}}rl}{{{g}_{0}}}\cdot \frac{4}{\text{ }\!\!\pi\!\!\text{ }}NNr=Lsrm$
(16) ${{L}_{Sr}}={{L}_{{{_{S}}_{rm}}}}\left( \begin{matrix} 1 & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & \cos \frac{4\text{ }\!\!\pi\!\!\text{ }}{3} \\ \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & 1 & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} \\ \cos \frac{4\text{ }\!\!\pi\!\!\text{ }}{3} & \cos \frac{2\text{ }\!\!\pi\!\!\text{ }}{3} & 1 \\ \vdots & \vdots & \vdots \\ \cos \frac{11\text{ }\!\!\pi\!\!\text{ }}{6} & \cos \frac{7\text{ }\!\!\pi\!\!\text{ }}{6} & 0 \\\end{matrix} \right)$
3.3 直线式移相变压器的边端效应及优化方案
由于直线式移相变压器的铁心存在纵向和横向两个边端,产生边端效应[18 ,19 ] 。横向边端效应主要是由于原边副边的宽度不相等导致部分铁心及导体悬引出去而引起的,纵向边端效应是由于行波磁场的运动方向两端开口造成的。由于横向方向导体没有切割磁感线,因此不考虑横向边端效应,只考虑纵向边端效应。
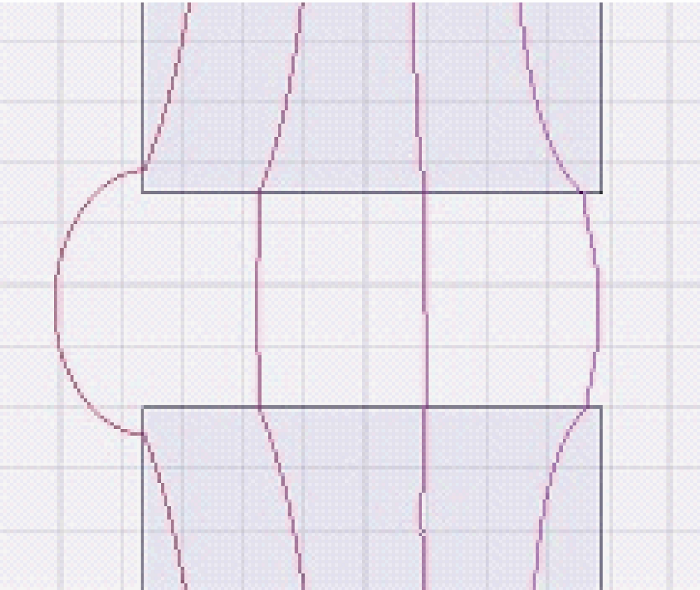
由于磁场在铁磁材料拐角处会增强,为了便于研究,本文把具有有限长的开磁路铁心的直线式移相变压器原边绕组在副边所产生的磁通密度空间分布近似看成折线,如图4 所示。在此忽略由于原边电路因素的不对称而产生的磁通脉动分量和槽脉动,且铁心两端磁通密度的增加当作直线状。
图4
现设想气隙磁通如图4 所示,在副边导体铁心两端的磁通密度大小变化区域,即在图4 中x 1 、x 2 和x 3 、x 4 间,由于副边导体中磁通密度的空间变化而感应出电动势,并由于副边负载电流性质不同,造成附加损耗。
对于直线电动机而言,导体随转子移动,必然会经过边端效应作用区域。但是对于本文的研究对象直线式移相变压器来说,其导体固定不动,如果导体在中间无边端效应的区域,就不会感应出由边端效应引起的电势。那么可以通过使气隙减小的同时,让边齿大一些,使得导体不在边端效应作用区域。理论上可以消除边端效应的影响。
图5 是边齿小、气隙大情况下的磁力线分布,此时边端的磁场在气隙部分有一些发散,边端效应影响很明显;图6 是在边齿大、气隙小情况下的磁力线分布,此时边端磁场在气隙部分的发散情况有了明显的改善,边端效应影响大大削弱了。
图5
图6
3.4 气隙及齿槽对齐方式对逆变系统的影响
直线式移相变压器由于不需要移动,其气隙可以远小于直线电动机和旋转电动机,理论上甚至可以为0。气隙及齿槽对齐方式影响着变压器的工作效率和输出电压的谐波。综合考虑二者,推导出气隙为0.3 mm时、齿槽与齿槽对齐时逆变效果最好,具体数据见表2 、3。
4 仿真结果
在Matlab中建立仿真模型,选择电压型三相全桥方波逆变器作为输入方波逆变器,使得导通角可以实现0°~180°大范围调节。方波逆变器输入直流电压E d =100 V,三相负载是对称负载。直线式移相变压器由4组三相全桥方波逆变器提供移相方波电压,输入方程及输出方程都为电压电流的微分方程,通过Matlab中s函数来求解。
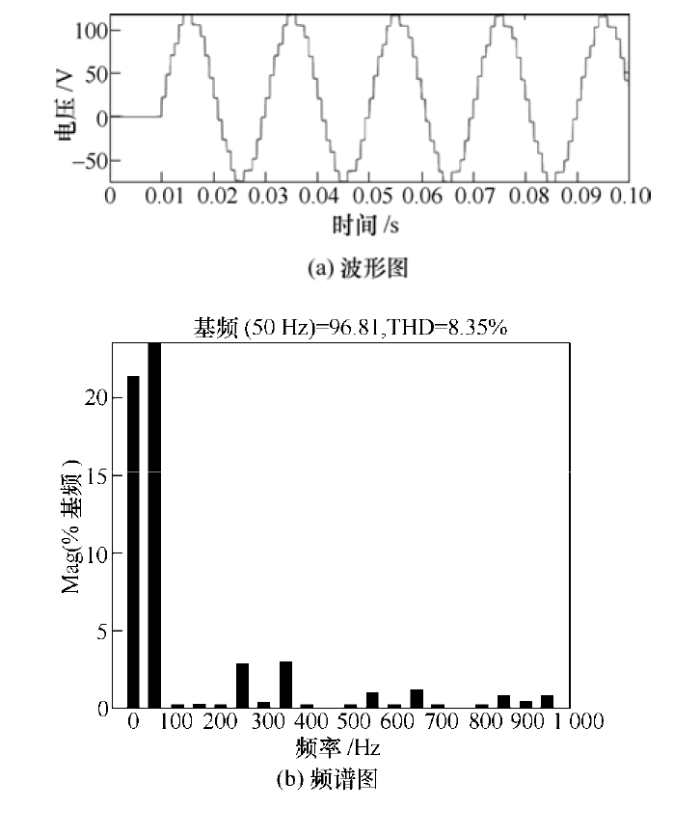
见图7 ,空载输出电压为标准的多阶梯波。对所得波形进行FFT分析,谐波以5、7次为主,还有少量11、13、17次谐波。当系统带额定负载时,输出波形见图8 ,由于感性负载有一定的滤波作用,因此输出波形更为平滑接近正弦波形。
图7
图8
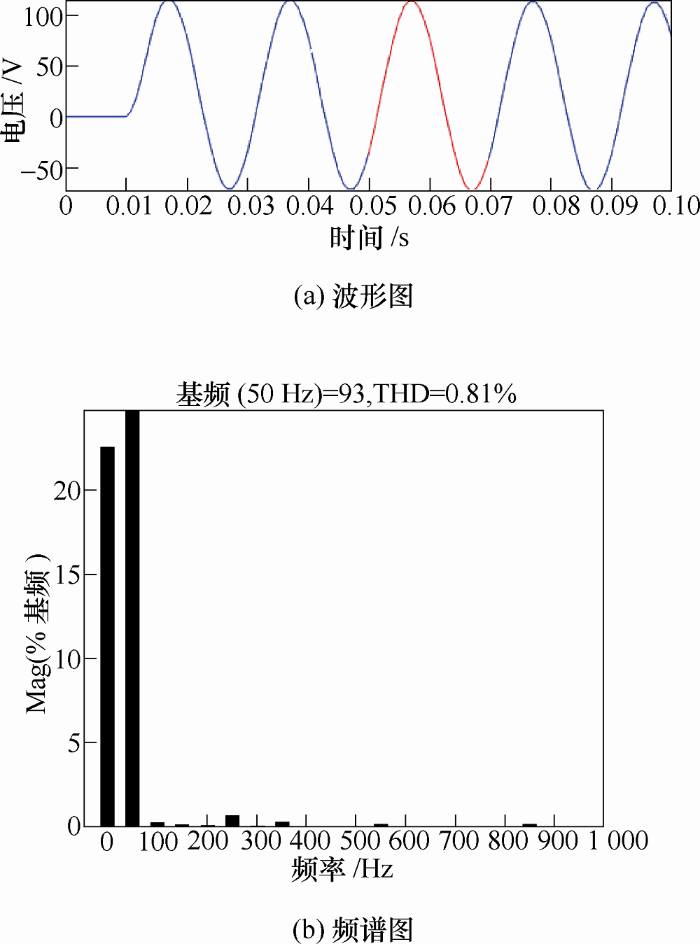
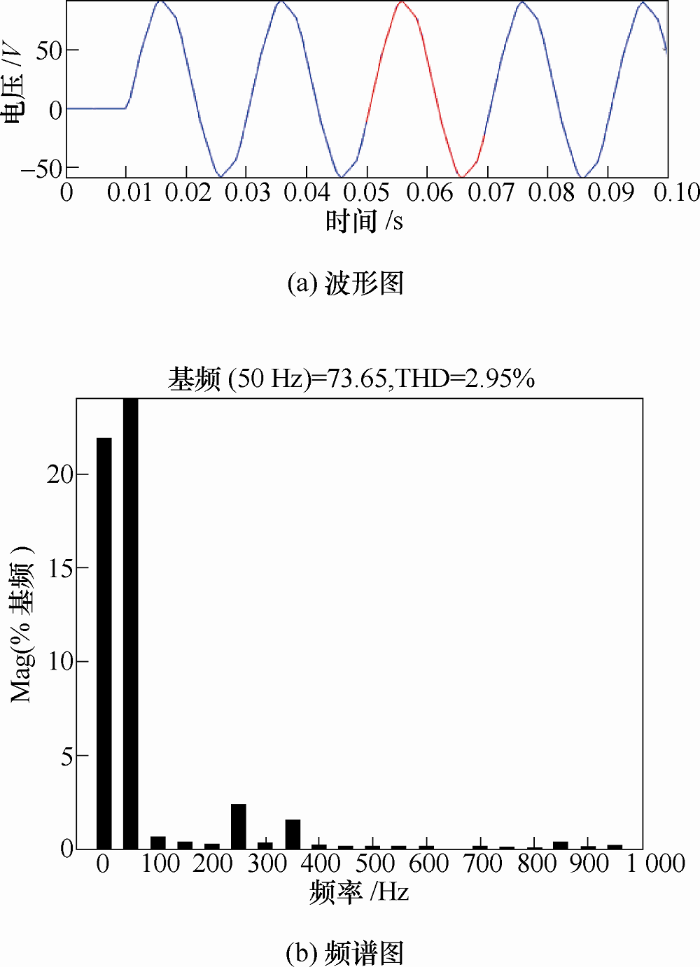
传统移相变压器的调压涉及到对变压器本体结构上做出改变,实现起来较困难。对于本课题的直线式移相变压器,改变方波电压输入的导通角就可以实现改变输出电压的大小。如图9 所示。从波形图可见,导通角调整对于本研究直线式移相变压器的谐波消除过程影响较小,输出电压波形的品质仍然很好。
图9
5 试验分析
本课题组为了验证理论与仿真分析的准确性,搭建了一台小容量的直线式移相变压器的试验样机,由于目前处于研究的初期阶段,对于此种结构形式的变压器容量及电压范围暂未确定。试验样机的具体设计参数见表4 。
图10 左边是各线圈绕组接线端,统一接到接线柱上,便于接线以及修改接线方式,图片右边即为直线式移相变压器铁心及变压器绕组,图10 中变压器上两根短线是为了便于移动变压器而设计的。
图10
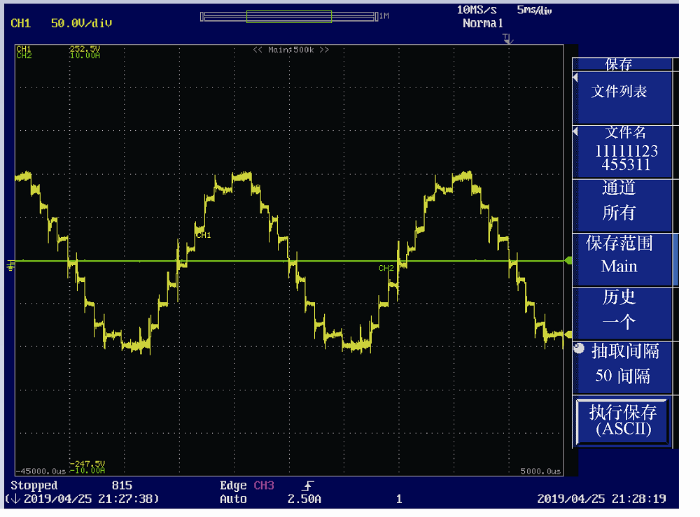
在理论与仿真分析的基础上,本课题组通过试验验证了直线式移相变压器逆变系统在空载运行时的工况。空载时的电压波形是明显的多阶梯波,如图11 所示,验证了理论与仿真分析的准确性。
图11
6 结论
针对传统移相变压器存在的问题,本课题组提出了一种新型的基于多重叠加逆变的直线式移相变压器。与传统移相变压器相比,直线式移相变压器体积更小、易于拓展、气隙磁场便于调节。不同于有限元分析方法,通过理论推导建立模型之后在Matlab中分析求解,所得到的结果更精确,波形质量更高。
参考文献
View Option
[1]
文小玲 , 尹项根 . 大容量多重化逆变器的输出电压谐波分析
[J]. 高电压技术 , 2007 ,33 (10 ):191 -197 .
[本文引用: 1]
Wen Xiaoling Yin Xianggen . Analysis of output voltage harmonic of large capacity multiple inverter
[J]. High Voltage Engineering , 2007 ,33 (10 ):191 -197 .
[本文引用: 1]
[2]
刘凤君 . 现代逆变技术及应用 [M]. 北京 : 电子工业出版社 , 2006 .
[本文引用: 1]
[3]
曲学基 , 曲敬铠 , 于明扬 . 逆变技术基础与应用 [M]. 北京 : 电子工业出版社 , 2006 .
[本文引用: 1]
[4]
陈坚 , 康勇 . 电力电子学——电力电子变换和控制技术 [M]. 北京 : 高等教育出版社 , 2011 .
[本文引用: 1]
[5]
沈冬珍 . 移相迭加阶梯波逆变器的分析和设计
[J]. 南京航空航天大学学报 , 1980 (1 ):105 -116 .
[本文引用: 1]
Shen Dongzhen . Analysis and design of phase-shifting and adding step wave inverter
[J]. Journal of Nanjing University of Aeronautics and Astronautics , 1980 (1 ):105 -116 .
[本文引用: 1]
[6]
王铁军 , 饶翔 , 姜小弋 . 用于多重化逆变的移相变压器
[J]. 电工技术学报 , 2012 ,27 (6 ):32 -37 .
Magsci
[本文引用: 1]
在多重化逆变中, 需要移相变压器把多相逆变器输出的非正弦电压进行合成, 使输出电压为接近正弦的多阶梯波形。为了改善结构和电气性能, 该文提出了一种新型磁路结构的移相变压器, 和普通移相整流变压器相比, 新型变压器铁心为圆形结构, 整体结构更为紧凑和对称, 电路结构更为简单。针对双Y/Y绕组变压器, 理论证明了5次、7次等主要低次谐波被消除, 合成磁动势为一接近圆形的旋转矢量, 并数值仿真分析了不同类型谐波电流所生成的磁场的性质。给出了由新型变压器构成的多重化逆变器的数学模型并对基本特性进行了仿真。最后, 基于多重化逆变系统, 实验验证了新型移相变压器的有效性, 结合设计对主要性能进行了分析。
Wang Tiejun Rao Xiang Jiang Xiaoyi . Phase-shifting transformer for multiplexed inverter
[J]. Transactions of China Electrotechnical Society , 2012 ,27 (6 ):32 -37 .
Magsci
[本文引用: 1]
在多重化逆变中, 需要移相变压器把多相逆变器输出的非正弦电压进行合成, 使输出电压为接近正弦的多阶梯波形。为了改善结构和电气性能, 该文提出了一种新型磁路结构的移相变压器, 和普通移相整流变压器相比, 新型变压器铁心为圆形结构, 整体结构更为紧凑和对称, 电路结构更为简单。针对双Y/Y绕组变压器, 理论证明了5次、7次等主要低次谐波被消除, 合成磁动势为一接近圆形的旋转矢量, 并数值仿真分析了不同类型谐波电流所生成的磁场的性质。给出了由新型变压器构成的多重化逆变器的数学模型并对基本特性进行了仿真。最后, 基于多重化逆变系统, 实验验证了新型移相变压器的有效性, 结合设计对主要性能进行了分析。
[7]
Bresesti P Sforna M Allegranza V et al . Application of phase shifting transformers for a secure and efficient operation of the interconnection corridors
[C]// Power Engineering Society General Meeting. IEEE , 2004 .
[本文引用: 1]
[8]
柳泊 . 圆形移相变压器及其在多重叠加逆变器中的应用
[M]. 武汉:海军工程大学 , 2014 .
[本文引用: 1]
[9]
魏永清 , 张晓峰 , 乔鸣忠 . 采用参考电压调节的并联逆变器控制技术
[J]. 电机与控制学报 , 2011 ,15 (2 ):84 -88 .
[本文引用: 1]
Wei Yongqing Zhang Xiaofeng Qiao Mingzhong . Control Technology of parallel inverter with reference voltage regulation
[J]. Journal of Electric Machines and Control , 2011 ,15 (2 ):84 -88 .
[本文引用: 1]
[10]
梁中华 , 于平泳 , 刘春芳 . 多重化逆变器及其控制方法
[J]. 沈阳工业大学学报 , 2009 ,31 (3 ):262 -266 .
[本文引用: 1]
Liang Zhonghua Yu Pingyong Liu Chunfang . Multiple inverters and their control methods
[J]. Journal of Shenyang University of Technology , 2009 ,31 (3 ):262 -266 .
[本文引用: 1]
[11]
郑立波 , 汪飞 , 何湘宁 . 多重化逆变器控制方法的研究
[J]. 电力电子技术 , 2008 ,38 (1 ):23 -25 .
[本文引用: 1]
Zheng Libo Wang Fei He Xiangning . Research on control method of multiple inverter
[J]. Power Electronics , 2008 ,38 (1 ):23 -25 .
[本文引用: 1]
[12]
楚冰清 . 基于移相控制的三相电流型多重化并网逆变器的仿真研究
[D]. 呼和浩特:内蒙古工业大学 , 2015 .
[本文引用: 1]
[13]
高志刚 , 张雷 , 付勋波 . 适合于并网型多重化逆变器的调制方法
[J]. 电网技术 , 2008 ,32 (20 ):64 -67 .
Magsci
[本文引用: 1]
并网型多重化逆变器各逆变桥的输出经变压器耦合后接入电网,提高了并网逆变器的容量等级。针对两单元多重化逆变器,提出一种载波相移正弦调制方法,可以在低次开关频率下提高系统的等效开关频率,提高各逆变器组工作的一致性,实现更好的谐波相抵效果,具有更快的实时性。最后进行了实验验证,该方法还可扩充应用到n单元并网型多重化逆变器中,应用前景好。
Gao Zhigang Zhang Lei Fu Xunbo . Modulation method suitable for grid-connected multiple inverters
[J]. System Technology , 2008 ,32 (20 ):64 -67 .
Magsci
[本文引用: 1]
并网型多重化逆变器各逆变桥的输出经变压器耦合后接入电网,提高了并网逆变器的容量等级。针对两单元多重化逆变器,提出一种载波相移正弦调制方法,可以在低次开关频率下提高系统的等效开关频率,提高各逆变器组工作的一致性,实现更好的谐波相抵效果,具有更快的实时性。最后进行了实验验证,该方法还可扩充应用到n单元并网型多重化逆变器中,应用前景好。
[14]
胡亮 , 胡绪昌 , 王铁军 . 一种应用于多重化逆变的变压器研究
[J]. 船电技术 , 2010 ,30 (7 ):29 -32 .
[本文引用: 1]
Hu Liang Hu Xuchang Wang Tiejun . Research on a transformer applied to multiple inverters
[J]. Marine Electric Technology , 2010 ,30 (7 ):29 -32 .
[本文引用: 1]
[15]
Toliyay H A Lipo T A White J C . Analysis of a concentrated winding induction machine for adjustable speed drive application part Ⅱ(Motor design and performance)
[J]. IEEE Transaction on Energy Conversion , 1991 ,6 (4 ):684 -692 .
[本文引用: 1]
[16]
Toliyay H A Lipo T A White J C . Analysis of a concentrated winding induction machine for adjustable speed drive application part Ⅰ(Motor design and performance)
[J]. IEEE Transaction on Energy Conversion , 1991 ,6 (4 ):679 -684 .
[本文引用: 1]
[17]
孙灏 . 基于电磁特性分析的直线电机边端效应研究
[D]. 天津:河北工业大学 , 2014 .
[本文引用: 1]
[18]
周挺 , 徐昕 , 孙明灿 . 轴向磁通永磁电机气隙磁场端部效应研究
[J]. 微电机 , 2016 ,49 (3 ):14 -17 .
[本文引用: 1]
Zhou Ting Xu Wei Sun Mingcan . Study on the end effect of air gap magnetic field in axial flux permanent magnet motor
[J]. Micromotors , 2016 ,49 (3 ):14 -17 .
[本文引用: 1]
大容量多重化逆变器的输出电压谐波分析
1
2007
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
大容量多重化逆变器的输出电压谐波分析
1
2007
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
1
2006
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
1
2006
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
1
2011
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
移相迭加阶梯波逆变器的分析和设计
1
1980
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
移相迭加阶梯波逆变器的分析和设计
1
1980
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
用于多重化逆变的移相变压器
1
2012
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
用于多重化逆变的移相变压器
1
2012
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
Application of phase shifting transformers for a secure and efficient operation of the interconnection corridors
1
2004
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
圆形移相变压器及其在多重叠加逆变器中的应用
1
2014
... 在工业、国防等领域中,高电压、大功率电能的获取目前普遍采用合成多阶梯波的手段来实现.多电平技术和多重叠加技术[1 ] 是获取多阶梯波的两种主要途径.多电平技术的原理是采用适当的拓扑结构,直接进行多重叠加或者直接输出阶梯波.这种拓扑结构可以降低开关管承受的直流母线电压,增加输出功率,因此多用于大功率逆变场合[2 ,3 ,4 ] .但多电平电路对器件的需求量与电平数的平方成正比,且结构与控制的复杂程度大大提高,并存在钳位电压均压等问题,因此实际应用中多电平电路一般不超过五电平.移相多重叠加的基本原理是把n 个完全相同的m 相方波或阶梯数较少的阶梯波,通过移相变压器依次移相180°/nm 的相位角,再叠加合成2nm 阶梯波[5 ,6 ,7 ] ,使得低次的谐波反相位而相互抵消,从而得到谐波含量较少的准正弦阶梯波.对于传统的多重叠加逆变器,通过对绕组间的串联次序、联结方式、匝数比等进行特殊设计之后,可以基本实现消除高次谐波并保持三相输出的对称性,但采用特殊设计后的变压器结构复杂、体积较大,不适合实际生产应用.传统移相变压器存在绕组绕线方式复杂、铁心利用率低、电流不均衡等问题.为了提高移相变压器的效率、改善其结构,并考虑到直线式结构易于拓展、绕组接线简单的优点,海军工程大学柳泊[8 ] 提出了一种直线式移相变压器,这种新型变压器是在圆形移相变压器的结构之上改进得到的.通过螺栓把它的初级铁心和次级铁心固定在一起,使其相对静止,使得调节变压器原副边间的垫片厚度可以改变气隙的大小.此外,串并联多个直线式移相变压器可以得到高电压、大电流.本研究目前开展的工作主要包括以下几点:① 介绍了新型移相变压器的结构与工作原理;② 给出了12/3相直线式移相变压器的模型与参数,并建立了仿真模型;③ 在仿真的基础上进行了试验分析. ...
采用参考电压调节的并联逆变器控制技术
1
2011
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
采用参考电压调节的并联逆变器控制技术
1
2011
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
多重化逆变器及其控制方法
1
2009
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
多重化逆变器及其控制方法
1
2009
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
多重化逆变器控制方法的研究
1
2008
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
多重化逆变器控制方法的研究
1
2008
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
基于移相控制的三相电流型多重化并网逆变器的仿真研究
1
2015
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
适合于并网型多重化逆变器的调制方法
1
2008
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
适合于并网型多重化逆变器的调制方法
1
2008
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
一种应用于多重化逆变的变压器研究
1
2010
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
一种应用于多重化逆变的变压器研究
1
2010
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
Analysis of a concentrated winding induction machine for adjustable speed drive application part Ⅱ(Motor design and performance)
1
1991
... 目前传统的逆变器输出大多为矩形波或阶梯数较少的阶梯波,里面含有大量5、7、11、13次等谐波,这些谐波严重降低了负载的性能、影响正常工作.为得到满足负载要求的电压或电流,人们提出了移相多重叠加法消除谐波[9 ,10 ,11 ,12 ,13 ,14 ,15 ] .本文提出一种新型的基于直线式移相变压器的逆变系统,见图1 ,与普通移相变压器相比,变压器结构和绕组接线方面都得到了优化,如表1 所示. ...
Analysis of a concentrated winding induction machine for adjustable speed drive application part Ⅰ(Motor design and performance)
1
1991
... 通过绕组函数分析方法来计算本模型中各绕组的自感及互感参数[16 ,17 ] ,初级侧12相整距绕组中,第i 相的自感为 ...
基于电磁特性分析的直线电机边端效应研究
1
2014
... 通过绕组函数分析方法来计算本模型中各绕组的自感及互感参数[16 ,17 ] ,初级侧12相整距绕组中,第i 相的自感为 ...
轴向磁通永磁电机气隙磁场端部效应研究
1
2016
... 由于直线式移相变压器的铁心存在纵向和横向两个边端,产生边端效应[18 ,19 ] .横向边端效应主要是由于原边副边的宽度不相等导致部分铁心及导体悬引出去而引起的,纵向边端效应是由于行波磁场的运动方向两端开口造成的.由于横向方向导体没有切割磁感线,因此不考虑横向边端效应,只考虑纵向边端效应. ...
轴向磁通永磁电机气隙磁场端部效应研究
1
2016
... 由于直线式移相变压器的铁心存在纵向和横向两个边端,产生边端效应[18 ,19 ] .横向边端效应主要是由于原边副边的宽度不相等导致部分铁心及导体悬引出去而引起的,纵向边端效应是由于行波磁场的运动方向两端开口造成的.由于横向方向导体没有切割磁感线,因此不考虑横向边端效应,只考虑纵向边端效应. ...