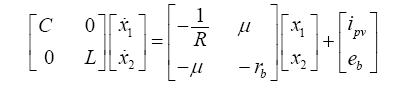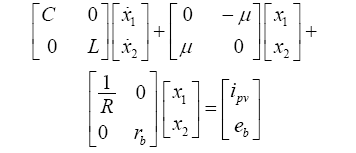1 引言
在微电网系统中,光伏发电作为一种重要的新能源发电方式,目前应用领域不断扩大。当光照和负载等发生变化时容易引起光伏系统不稳定,导致输出电压波动较大。下垂控制作为光储微网主流的控制方式,当系统负荷有扰动时,电压波动较大,低频减载设备难以快速消除扰动,阻碍电网维持稳定状态[1 ] 。随着光伏电网规模的不断扩大,如何维持光储微网的稳定高效运行是值得进一步探究的问题。
微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] 。在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略。文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能。但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来。文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果。但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整。文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制。但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器。
近几年,一些更为先进的非线性控制算法也逐渐应用到光储微电网的控制中,文献[6 ]将无源控制理论应用于微电网中,在此论文中,首先将微电网系统的数学模型写成哈密顿方程,结合哈密顿方程和系统的无源性设计了系统无源控制器,能够较好地实现在弱光照强度下蓄电池放电,强光照情况下蓄电池充电,同时保证直流负载侧电压稳定,系统也具有较好的鲁棒性能,但是所设计的控制器并不能满足系统对控制器有界的要求,这使得在蓄电池在充放电转换过程中会有较大的电压脉冲。文献[7 ]通过建立光储微网的仿射非线性模型,通过无源控制理论验证了光储微网系统的无源性,并采用基于无源性小增益控制策略设计控制器,使得系统满足了对控制器有界的要求,在一定程度上提高了控制性能,但设计过程较为繁琐,控制器需要利用系统中较多参数变量,这使得控制器可实现性较差,且整体控制效果有待进一步提高。
基于无源控制(Passivity-based control,PBC)设计作为一种本质上的非线性控制方法[8 ] ,目前在电气控制领域得到了越来越广泛的应用,如文献[9 ]通过建立光伏并网逆变器的EL功率模型,并通过光伏阵列MPPT的最大功率计算出光伏并网逆变器期望最大输出功率,设计了光伏并网逆变器无源功率控制器,得到了非常好的控制效果。基于此,本文将基于EL模型的无源控制策略应用到光储微网系统中,首先分析了双向DC-DC变换器在充、放电时的两种工作状态;其次通过建立光储微网控制系统的EL模型,采用注入阻尼法设计了双向DC-DC变换器无源控制器;最后,通过搭建Simulink仿真模型,验证本文所提出控制策略的正确性和可行性。
2 光储微网系统结构及变换器工作状态分析
2.1 光储微网系统结构
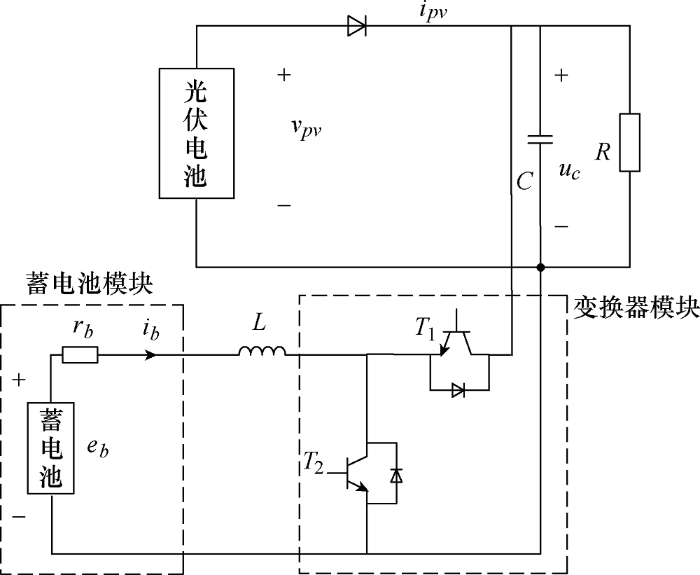
光储微网主电路结构主要由光伏电池、蓄电池、DC-DC变换器和控制器组成,由于光储微网常常受环境、温度等外界条件影响,在微网系统中加入储能元件可以方便进行功率平衡。系统结构如图1 所示。
图1
双向DC-DC变换器的主要功能是控制蓄电池的充电和放电,实现控制能量双向流动。在系统运行过程中,通过检测光照强度变化,当光照强度低于设定值时,双向DC-DC变换器工作在Boost状态,蓄电池向负载供能;当光照强度高于设定值时,双向DC-DC变换器工作在Buck状态,将多余的电能存储于蓄电池中,从而保证系统的平稳运行,提高系统安全性和可靠性。在实际应用中,可以根据实际负载的额定功率来配置光伏电池,充分发挥双向DC-DC变换器和蓄电池的能量管理功能,在保证稳定性和可靠性的同时降低系统的配置和运行成本[10 ] 。
2.2 双向DC-DC变换器模型及工作状态分析
在光储微电网中,蓄电池储能系统具备吸收和释放功率的能力,因此需要使用具有双向流动性的变换器,实现能量的双向流通。本文主要针对恒定直流负载进行研究,变换器选用双向DC-DC变换器。
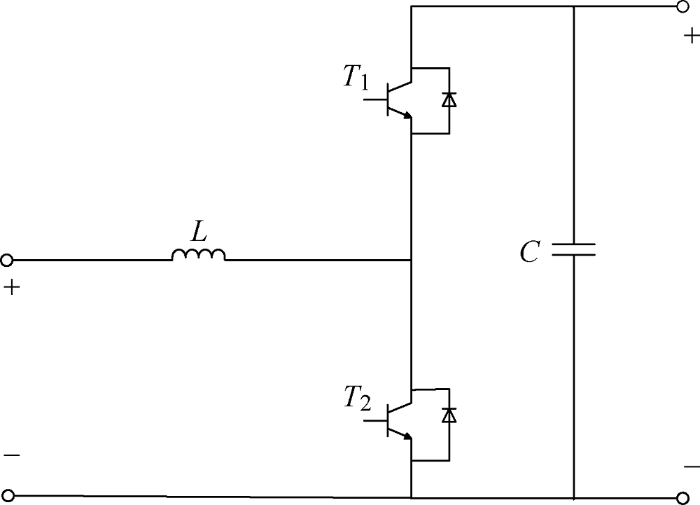
双向半桥式DC-DC变换器结构比较简单、元件少,能够高效完成不同状态的快速切换。在实际工程应用中,如果将这种拓扑结构进行串并联组合,可以得到变比和耐压等级更高的双向DC-DC变换器,使得输出的电压纹波和电流纹波更小[11 ] 。采用的双向DC-DC变换器结构如图2 所示。
图2
双向DC-DC变换器由电感器、电容器以及两个开关器件组成,既可以工作在升压状态(Boost)也可以工作在降压状态(Buck),与蓄电池的放电状态和充电状态相对应。为了避免蓄电池受到高压的冲击,蓄电池两端的电压比较低,相对应负载侧的电压来说,从蓄电池端流向负载侧是升压状态,此时T 2 导通,T 1 关断;从光伏电池侧流向蓄电池侧属于降压状态,此时T 1 导通,T 2 关断。
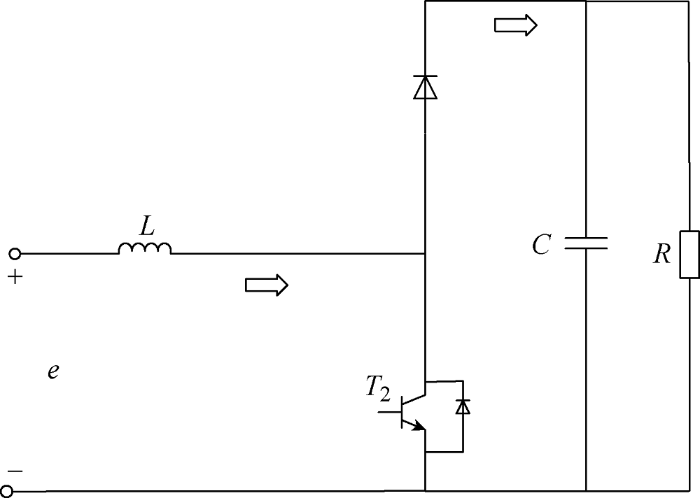
对电路Buck、Boost状态进行分析,当光照强度较强,光伏电池输出电压偏高、功率过多的情况下,需要将多余的能量通过双向DC-DC变换器储存在蓄电池中。此时,双向DC-DC变换器的T 1 管工作,T 2 管关断,工作在降压状态,通过调节T 1 管的占空比将光伏电池输出的电压降低到蓄电池的充电电压,蓄电池完成充电过程。DC-DC变换器Buck状态下能量流向情况如图3 所示。
图3
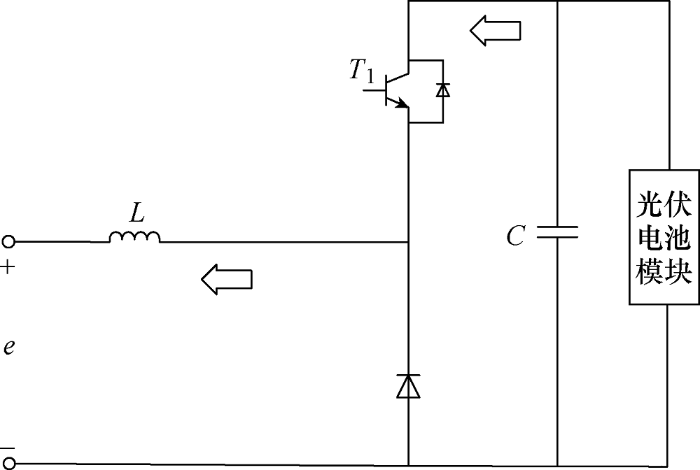
当光照强度较低时,光伏电池输出的电压比较低,输出功率不足以支持负载正常工作,需要蓄电池向负载供能。此时,双向DC-DC变换器的T 1 管关断,T 2 管工作,工作在升压状态,通过调节T 2 管的占空比将蓄电池的放电电压升高到负载正常工作的电压,从而实现能量从储能侧向负载侧的传输。DC-DC变换器Boost状态下能量流向情况如图4 所示。
图4
3 光储微网系统EL模型及无源控制器设计
3.1 光储微网系统EL模型
根据光储微网系统结构框图1 ,由基尔霍夫定律可以得到系统的数学表达式
(1) $\left\{ \begin{align} & C\frac{\text{d}{{u}_{c}}}{\text{d}t}={{i}_{pv}}-\frac{{{u}_{c}}}{R}+\mu {{i}_{b}} \\ & L\frac{\text{d}{{i}_{\text{b}}}}{\text{d}t}={{e}_{b}}-{{r}_{b}}{{i}_{b}}-\mu {{u}_{c}} \\ \end{align} \right.$
定义开关管驱动信号$\mu $,当双向DC-DC变换器工作在Boost状态时,T 1 管始终关断,当$\mu $=1时,T 2 管关断,当$\mu $=0时,T 2 管导通;当工作在Buck状态时,T 2 管始终关断,当$\mu $=1时T 1 管导通,$\mu $=0时,T 1 管关断。工作于Buck状态下T 1 管的驱动信号与工作于Boost状态下T 2 管的驱动信号互补。
$x=\begin{bmatrix}x_{1}\\x_{2} \end{bmatrix}=\begin{bmatrix}u_{c}\\i_{b} \end{bmatrix}$
(2) $\left\{ \begin{align} & {{{\dot{x}}}_{1}}=\frac{1}{C}\left[ {{i}_{pv}}-\frac{{{x}_{1}}}{{{R}_{{}}}}+\mu {{x}_{2}} \right] \\ & {{{\dot{x}}}_{2}}=\frac{1}{L}({{e}_{b}}-{{r}_{b}}{{x}_{2}}-\mu {{x}_{1}}) \\ \end{align} \right.$
(3)
(4)
(5) ${{M}_{Bu}}\dot{x}+{{J}_{Bu}}x+{{R}_{Bu}}x={{u}_{Bu}}$
式中,${{M}_{Bu}}$为正定的对角阵;${{J}_{Bu}}$为反对称矩阵,${{J}_{Bu}}=-J_{Bu}^{\text{T}}$,反映了系统内部互联结构;${{R}_{Bu}}$为对称正定矩阵,反映了系统的耗散特性;系统与外部能量交换用${{u}_{Bu}}$表示。各矩阵具体表达式为
${{M}_{Bu}}=\left[ \begin{matrix} C & 0 \\ 0 & L \\\end{matrix} \right]$ ${{J}_{Bu}}=\left[ \begin{matrix} 0 & -\mu \\ \mu & 0 \\\end{matrix} \right]$
${{R}_{Bu}}=\left[ \begin{matrix} \frac{1}{R} & 0 \\ 0 & {{r}_{b}} \\\end{matrix} \right]$ ${{u}_{Bu}}=\left[ \begin{align} & {{i}_{pv}} \\ & {{e}_{b}} \\ \end{align} \right]$
3.2 控制系统无源性分析
如果存在一个正定函数,$Q(x):{{\mathbf{R}}^{n}}\to R$对$\forall t>0$时所有的$u\in {{\mathbf{R}}^{m}}$和所有的${{x}_{0}}\in {{\mathbf{R}}^{n}}$,得到下列耗散不等式[12 ]
(6) $H({{x}_{t}})-H({{x}_{0}})\le {{\int_{0}^{t}{u}}^{\text{T}}}y\text{d}\tau -\int_{0}^{t}{Q(x)\text{d}\tau }$
(7) $\dot{H}\le {{u}^{\text{T}}}y-Q(x)$
对系统的输入、输出以及能量供给率成立,则系统被称为是严格无源的,可解释为伴随着输入$u$由外部注入到系统的能量供给率,$H$为系统能量的存储函数。式(6)、式(7)被称为严格无源不等式。
(8) $H=\frac{1}{2}{{x}^{\text{T}}}{{M}_{Bu}}x$
(9) $\dot{H}={{x}^{\text{T}}}{{M}_{Bu}}x={{x}^{\text{T}}}({{u}_{Bu}}-{{J}_{Bu}}x-{{R}_{Bu}}x)$=${{x}^{\text{T}}}{{u}_{Bu}}-{{x}^{\text{T}}}{{R}_{Bu}}x$
令$y=x$,$Q(x)={{x}^{\text{T}}}{{R}_{Bu}}x$,结合式(7),可以看出控制系统是严格无源的。
3.3 无源控制器设计
设期望的状态矢量为${{x}^{*}}=[x_{1}^{*}\,\ x_{2}^{*}]$,状态矢量误差$e=x-{{x}^{\mathbf{*}}}$。${{x}^{*}}$为系统的期望平衡点,$x_{1}^{*}$为负载理想工作电压,令$x_{1}^{*}={{V}_{d}}$,且$\dot{x}_{1}^{*}=0$,结合式(2)可得
(10) $\left\{ \begin{align} & \frac{{{V}_{d}}}{R}-{{i}_{pv}}={{\mu }^{*}}x_{2}^{*} \\ & {{e}_{b}}-{{r}_{b}}x_{2}^{*}={{\mu }^{*}}{{V}_{d}} \\ \end{align} \right.$
令$x_{2}^{*}={{I}_{d}}$,由式(10)得
(11) ${{I}_{d}}=\frac{{{e}_{b}}\pm \sqrt{e_{b}^{2}-4{{r}_{b}}{{V}_{d}}\left( \frac{{{V}_{d}}}{R}-{{i}_{pv}} \right)}}{2{{r}_{b}}}$
将$e=x-{{x}^{\mathbf{*}}}$代入到式(5)EL模型中可得
(12) ${{M}_{Bu}}\dot{e}+{{J}_{Bu}}e+{{R}_{Bu}}e$=$u-\text{ }\!\![\!\!\text{ }{{M}_{Bu}}{{\dot{x}}^{\mathbf{*}}}+{{J}_{Bu}}{{x}^{\mathbf{*}}}+{{R}_{Bu}}{{x}^{\mathbf{*}}}\text{ }\!\!]\!\!\text{ }$
由式(9)可看出系统的收敛速度与${{R}_{Bu}}$的大小有密切联系,所以在此采用注入阻尼的方法来加快
(13) ${{M}_{Bu}}\dot{e}+{{J}_{Bu}}e+{{R}_{Bu}}e+{{R}_{a}}e$=$u-\text{ }\!\![\!\!\text{ }{{M}_{Bu}}{{\dot{x}}^{\mathbf{*}}}+{{J}_{Bu}}{{x}^{\mathbf{*}}}+{{R}_{Bu}}{{x}^{\mathbf{*}}}\text{ }\!\!]\!\!\text{ }+{{R}_{a}}e$
其中,注入阻尼 $R_{a}=\begin{bmatrix}R_{a1} && 0 \\ 0 && R_{a2} \end{bmatrix}$。
(14) $u={{M}_{Bu}}{{\dot{x}}^{\mathbf{*}}}+{{J}_{Bu}}{{x}^{\mathbf{*}}}+{{R}_{Bu}}{{x}^{\mathbf{*}}}-{{R}_{a}}e$
(15) ${{M}_{Bu}}\dot{e}+{{J}_{Bu}}e+{{R}_{Bu}}e+{{R}_{a}}e=0$
取误差能量存储函数${{H}_{e}}(x)=\frac{1}{2}{{e}^{\text{T}}}{{M}_{Bu}}e$,则有
(16) ${{\dot{H}}_{e}}\text{(}x\text{)}={{e}^{\text{T}}}{{M}_{Bu}}\dot{e}=-{{e}^{\text{T}}}\text{(}{{R}_{Bu}}+{{R}_{a}}\text{)}e<0$
(17) $\left\{ \begin{align} & {{i}_{pv}}=C\dot{x}_{1}^{*}-\mu x_{2}^{*}+\frac{1}{R}x_{1}^{*}-{{R}_{a1}}({{x}_{1}}-x_{1}^{*}) \\ & {{e}_{b}}=L\dot{x}_{2}^{*}+\mu x_{1}^{*}+{{r}_{b}}x_{2}^{*}-{{R}_{a2}}({{x}_{2}}-x_{2}^{*}) \\ \end{align} \right.$
由式(17)得到控制律式(14)对应的开关管驱动信号
(18) $\left\{ \begin{align} & {{\mu }_{\text{1}1}}=\frac{\frac{{{V}_{d}}}{R}-{{R}_{a1}}({{u}_{c}}-{{V}_{d}})-{{i}_{pv}}}{{{I}_{d}}} \\ & {{\mu }_{\text{1}2}}=\frac{{{e}_{b}}-{{r}_{b}}{{I}_{d}}+{{R}_{a2}}({{i}_{b}}-{{I}_{d}})}{{{V}_{d}}} \\ \end{align} \right.$
将${{\mu }_{\text{11}}}$代入式(1)可得
(19) $\left\{ \begin{align} & C{{I}_{d}}\frac{\text{d}{{u}_{c}}}{\text{d}t}={{I}_{d}}({{i}_{pv}}-\frac{{{u}_{c}}}{R})+{{i}_{b}}(\frac{{{V}_{d}}}{R}-{{R}_{a1}}({{u}_{c}}-{{V}_{d}})-{{i}_{pv}}) \\ & L{{I}_{d}}\frac{\text{d}{{i}_{b}}}{\text{d}t}={{I}_{d}}({{e}_{b}}-{{r}_{b}}{{i}_{b}})-{{u}_{c}}(\frac{{{V}_{d}}}{R}-{{R}_{a1}}({{u}_{c}}-{{V}_{d}})-{{i}_{pv}}) \\ \end{align} \right.$
由式(19)可以看出,有阻尼注入时且由控制律式(14)得到的系统存在强耦合,将${{\mu }_{\text{12}}}$代入式(1)后同样如此。
(20) ${{M}_{Bu}}\dot{e}+{{R}_{Bu}}e+{{R}_{a}}e=u-$$\text{ }\!\![\!\!\text{ }{{M}_{Bu}}{{\dot{x}}^{\mathbf{*}}}+{{J}_{Bu}}({{x}^{\mathbf{*}}}+e)+{{R}_{Bu}}{{x}^{\mathbf{*}}}\text{ }\!\!]\!\!\text{ }+{{R}_{a}}e$
(21) $u'={{M}_{Bu}}{{\dot{x}}^{\mathbf{*}}}+{{J}_{Bu}}x+{{R}_{Bu}}{{x}^{\mathbf{*}}}-{{R}_{a}}e$
(22) $\left\{ \begin{align} & {{\mu }_{\text{21}}}=\frac{\frac{{{V}_{d}}}{R}-{{R}_{a1}}({{u}_{c}}-{{V}_{d}})-{{i}_{pv}}}{{{i}_{b}}} \\ & {{\mu }_{2\text{2}}}=\frac{{{e}_{b}}-{{I}_{d}}{{r}_{b}}+{{R}_{a2}}({{i}_{b}}-{{I}_{d}})}{{{u}_{c}}} \\ \end{align} \right.$
此时将${{\mu }_{\text{21}}}$代入式(1)可得
(23) $\left\{ \begin{align} & \frac{CR}{1+R{{R}_{a1}}}\frac{\text{d}{{u}_{c}}}{\text{d}t}+{{u}_{c}}={{V}_{d}} \\ & L{{i}_{b}}\frac{\text{d}{{i}_{b}}}{\text{d}t}={{i}_{b}}({{e}_{b}}-{{r}_{b}}{{i}_{b}})-{{u}_{c}}(\frac{{{V}_{d}}}{R}-{{R}_{a1}}({{u}_{c}}-{{V}_{d}})-{{i}_{pv}}) \\ \end{align} \right.$
当选择合适的注入阻尼${{R}_{a1}}$,${{u}_{c}}$很快收敛到${{V}_{d}}$,式(23)中第二个式子变为
(24) $L{{i}_{b}}\frac{\text{d}{{i}_{b}}}{\text{d}t}+{{r}_{b}}i_{b}^{2}-{{e}_{b}}{{i}_{b}}={{V}_{d}}{{i}_{pv}}-\frac{V_{d}^{2}}{R}$
式(24)反映了功率平衡,蓄电池电流${{i}_{b}}$可以快速跟踪期望电流${{I}_{d}}$。
同样将${{\mu }_{\text{22}}}$代入式(1)可得
(25) $\left\{ \begin{align} & \frac{L}{{{r}_{b}}+{{R}_{a2}}}\frac{\text{d}{{i}_{b}}}{\text{d}t}+{{i}_{b}}={{I}_{d}} \\ & C{{u}_{c}}\frac{\text{d}{{u}_{c}}}{\text{d}t}={{u}_{c}}({{i}_{pv}}-\frac{{{u}_{c}}}{R})+{{i}_{b}}({{e}_{b}}-{{I}_{d}}{{r}_{b}}+{{R}_{a2}}({{i}_{b}}-{{I}_{d}})) \\ \end{align} \right.$
可见当选择合适的注入阻尼${{R}_{a2}}$可使${{i}_{b}}$快速收敛到期望电流${{I}_{d}}$,同时第二个式子变为式(26),输出电压${{u}_{c}}$快速收敛到${{V}_{d}}$,满足功率平衡。
(26) $C{{u}_{c}}\frac{\text{d}{{u}_{c}}}{\text{d}t}+\frac{u_{c}^{2}}{R}-{{u}_{c}}{{i}_{pv}}={{I}_{d}}{{e}_{b}}-I_{d}^{2}{{r}_{b}}$
从理论上讲,选取合适的注入阻尼,可使${{u}_{c}}$快速收敛到${{V}_{d}}$,但实际上,${{u}_{c}}$的快速跟踪变化需要蓄电池电流${{i}_{b}}$的快速变化完成能量平衡。因此,在没有${{i}_{b}}$快速收敛的情况下,期望${{u}_{c}}$快速收敛到${{V}_{d}}$是不可实现的。
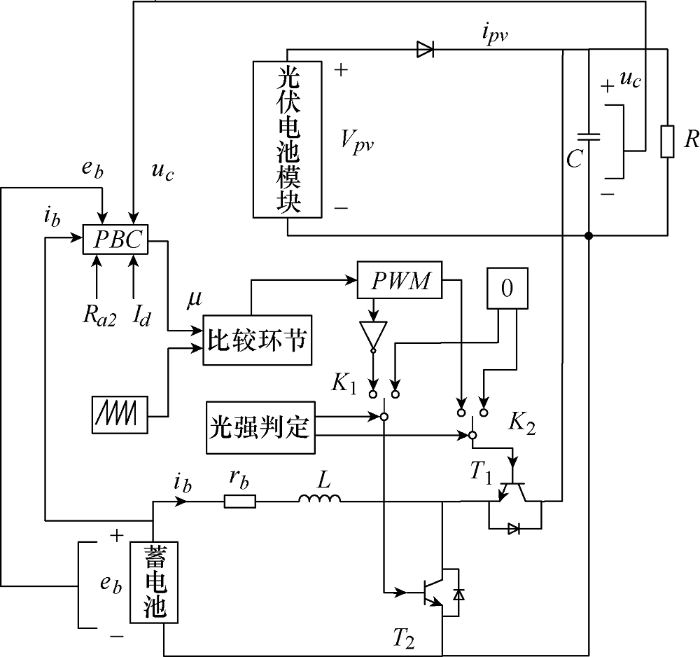
综上分析,由式(22)得到的开关管驱动信号${{\mu }_{\text{22}}}$搭建的光储微网系统控制框图如图5 所示。
图5
4 仿真研究
4.1 参数选择
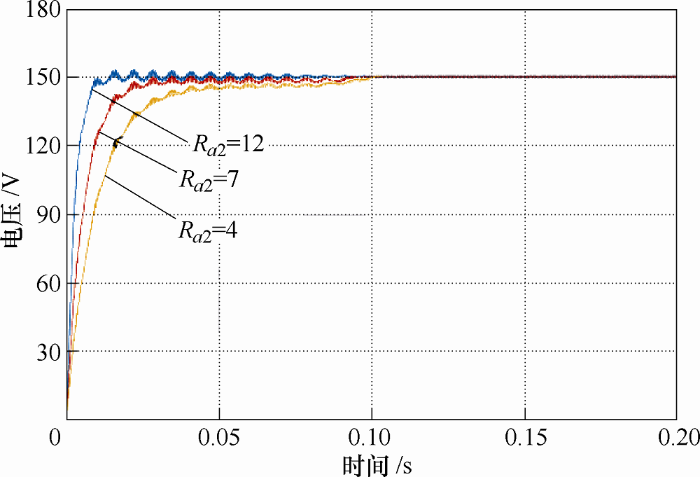
通过选取不同的注入阻尼参数,仿真试验比较系统输出电压响应曲线,可以看出注入阻尼参数的选取会对系统动态性有一定影响。注入阻尼参数越大,系统响应越快;注入阻尼参数越小,系统响应时间变长。系统注入阻尼参数的可行性范围为4~12,当${{R}_{a2}}<\text{4}$时,输出电压上升时间较长不能达到控制要求;当${{R}_{a2}}>\text{1}2$时,由于阻尼参数过大,控制效果不明显。不同阻尼参数下电压响应曲线如图6 所示。
图6
根据图5 ,利用Simulink中的电力电子模块搭建仿真模型进行验证,主要仿真参数如表1 所示。
4.2 仿真结果
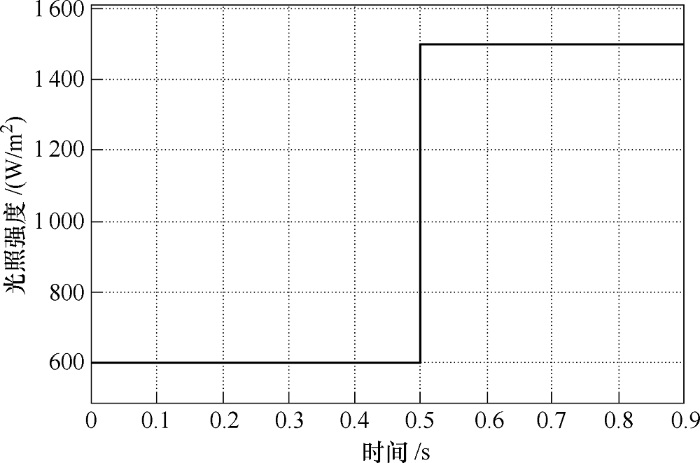
对光储微网无源控制系统进行仿真验证,在温度和负载保持不变的情况下,初始光照强度为600 W/m2 ,在运行至0.5 s时光照强度突然变化至1 500 W/m2 ,光照强度变化曲线如图7 所示。
图7
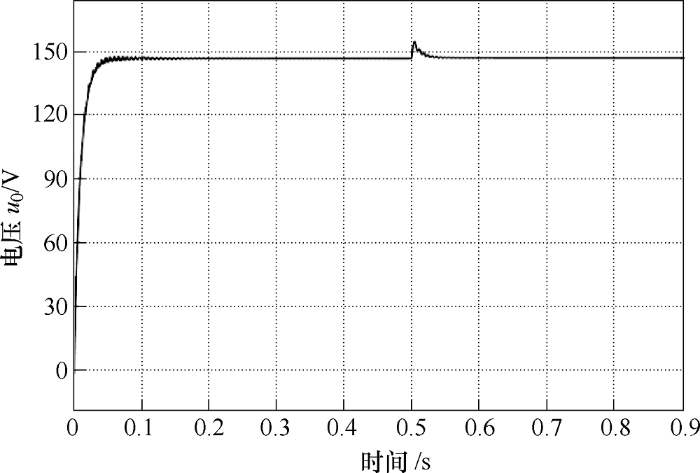
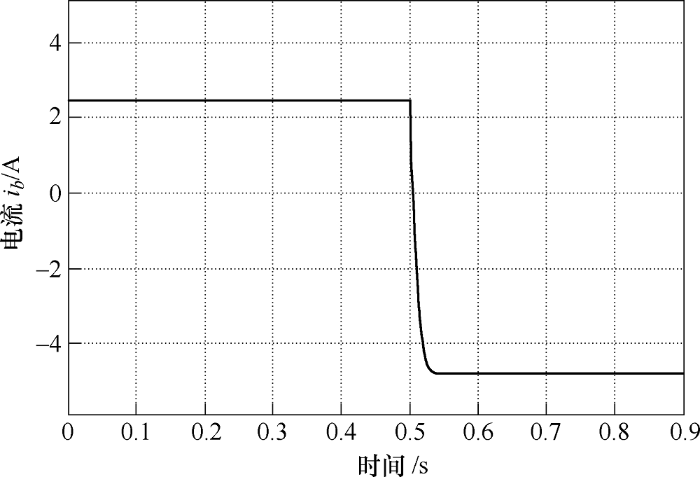
通过判断光照强度控制开关K1 、K2 选择开关管驱动信号,设定当光照强度小于1 000 W/m2 时,双向DC-DC变换器工作在Boost状态,T 1 管输入低电平,T 2 管输入驱动信号;当光照强度大于1 000 W/m2 时,双向DC-DC变换器工作在Buck状态,T 2 管输入低电平,T 1 管输入驱动信号。仿真得到光照强度突变下输出电压变化、蓄电池电流变化及蓄电池电量变化图如图8 ~10所示。
图8
图9
图10
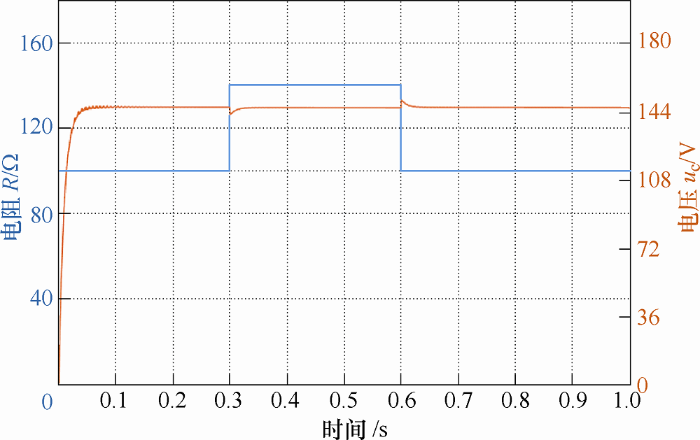
在保持光照强度不变的条件下,在0.3 s时负载值由100 Ω突变为140 Ω,在0.6 s时负载值由140 Ω突变为100 Ω,输出电压变化曲线如图11 所示。
图11
由图8 可见在光照强度发生剧烈变化时,负载电压能够快速跟踪到期望电压,保持输出电压稳定,且波动变化较小,控制效果理想。由图9 和图10 可见,在光照强度较弱时,蓄电池工作在放电状态,电流为正且电量下降;在突然大幅度增大光照强度后,蓄电池变为充电状态,电流为负且电池电量上升,通过设计无源控制器能够完成控制要求。在负载突然增大或减小时时,由图11 可见系统能够及时稳定输出电压,具有较好的鲁棒性能。
5 结论
本文基于EL模型设计了光储微电网的无源控制器,通过对光储微电网中系统结构及双向DC-DC变换器工作状态分析,建立起微网系统的EL模型,并采用阻尼注入的无源化设计方法设计了无源控制器。仿真结果表明,基于EL模型的光储微网控制器能够很好地完成控制任务,并具有较好的鲁棒性能。无源控制器的设计仍属于光储微网的1级控制,虽然能够保证系统的稳定运行,仍需结合其2、3级控制实现在交流电网存在时电压频率的修正以及与其他电网的协调控制,这也是值得进一步研究的内容。
参考文献
View Option
[1]
杨俊杰 . 光伏微网中下垂控制器的设计与优化
[D]. 哈尔滨:东北农业大学 , 2017 .
[本文引用: 1]
[2]
Bidram A Davoudi A . Hierarchical structure of microgrids control system
[J]. IEEE Transactions on Smart Grid , 2012 ,3 (4 ):1963 -1976 .
[本文引用: 1]
[3]
闫卫国 , 蒋菱 , 陈晓祺 , 等 . 孤立运行的低压微电网改进下垂控制策略
[J]. 电力系统及其自动化学报 , 2018 ,30 (6 ):45 -52 .
[本文引用: 1]
Yan Weiguo Jiang Ling Chen Xiaoqi , et al . Improved droop control strategy for islanded low-voltage microgrid
[J]. Proceedings of the CSU-EPSA , 2018 ,30 (6 ):45 -52 .
[本文引用: 1]
[4]
Mahmood H Michaelson D Jiang J . Accurate reactive power sharing in an islanded microgrid using adaptive virtual impedances
[J]. IEEE Trans on Power Electronics , 2015 ,30 (3 ):1605 -1617 .
[本文引用: 1]
[5]
申凯 . 基于下垂控制的微网逆变器双模式统一控制器研究
[D]. 合肥:合肥工业大学 , 2013 .
[本文引用: 1]
[6]
Becherif M Paire D Miraoui A Energy management of solar panel and battery system with passive control
[C]. International Conference on Clean Electrical Power,ICCEP'07. Capri,Italy , 2007 : 14 -19 .
[本文引用: 1]
[7]
胡丹 . 基于蓄电池储能的微电网控制系统设计
[D]. 哈尔滨:哈尔滨工业大学 , 2015 .
[本文引用: 1]
[8]
王久和 . 电能变换器及其无源控制 [M]. 北京 : 科学出版社 , 2014 .
[本文引用: 1]
[9]
王久和 , 慕小斌 , 张百乐 , 等 . 光伏并网逆变器最大功率传输控制研究
[J]. 电工技术学报 , 2014 ,29 (6 ):49 -56 .
Magsci
[本文引用: 1]
建立了光伏并网逆变器的EL功率模型。基于EL功率模型和无源控制理论,通过光伏阵列MPPT的最大功率计算光伏并网逆变器期望最大输出功率,利用阻尼注入方法设计了光伏并网逆变器无源功率控制器。该无源功率控制器可使光伏并网逆变器输出功率有效跟踪光伏阵列最大功率点的功率,进而实现最大功率传输;同时可实现网侧单位功率因数、电流低谐波。仿真及实验结果表明基于EL功率模型的无源功率控制器可实现光伏并网逆变器最大功率传输。
Wang Jiuhe Mu Xiaobin Zhang Baile , et al . Research on maximum power transfer control of photovoltaic grid connected inverters
[J]. Transactions of China Electrotechnical Society , 2014 ,29 (6 ):49 -56 .
Magsci
[本文引用: 1]
建立了光伏并网逆变器的EL功率模型。基于EL功率模型和无源控制理论,通过光伏阵列MPPT的最大功率计算光伏并网逆变器期望最大输出功率,利用阻尼注入方法设计了光伏并网逆变器无源功率控制器。该无源功率控制器可使光伏并网逆变器输出功率有效跟踪光伏阵列最大功率点的功率,进而实现最大功率传输;同时可实现网侧单位功率因数、电流低谐波。仿真及实验结果表明基于EL功率模型的无源功率控制器可实现光伏并网逆变器最大功率传输。
[10]
O Tremblay L-A Dessaint A-I Dekkiche A generic battery model for the dynamic simulation of hybrid electric vehicles
[C]// Vehicle Power and Propulsion Conference. 2007 : 284 -289 .
[本文引用: 1]
[11]
樊东东 . 用于电池储能系统的双向DC-DC变换器研究
[D]. 淮南:安徽理工大学 , 2017 .
[本文引用: 1]
[12]
王久和 . 先进非线性控制理论及其应用 [M]. 北京 : 科学出版社 , 2012 .
[本文引用: 1]
光伏微网中下垂控制器的设计与优化
1
2017
... 在微电网系统中,光伏发电作为一种重要的新能源发电方式,目前应用领域不断扩大.当光照和负载等发生变化时容易引起光伏系统不稳定,导致输出电压波动较大.下垂控制作为光储微网主流的控制方式,当系统负荷有扰动时,电压波动较大,低频减载设备难以快速消除扰动,阻碍电网维持稳定状态[1 ] .随着光伏电网规模的不断扩大,如何维持光储微网的稳定高效运行是值得进一步探究的问题. ...
Hierarchical structure of microgrids control system
1
2012
... 微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] .在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略.文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能.但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来.文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果.但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整.文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制.但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器. ...
孤立运行的低压微电网改进下垂控制策略
1
2018
... 微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] .在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略.文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能.但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来.文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果.但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整.文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制.但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器. ...
孤立运行的低压微电网改进下垂控制策略
1
2018
... 微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] .在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略.文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能.但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来.文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果.但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整.文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制.但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器. ...
Accurate reactive power sharing in an islanded microgrid using adaptive virtual impedances
1
2015
... 微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] .在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略.文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能.但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来.文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果.但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整.文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制.但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器. ...
基于下垂控制的微网逆变器双模式统一控制器研究
1
2013
... 微电网的控制系统根据功能一般可划分为3个层级:在第1层级中包含电流、电压和功率3个控制回路,第2层级负责对微电网中的电压及频率进行修正,第3层级对本地微电网与其他微电网或者上级电网进行协调[2 ] .在第1层级的功率控制回路中,多采用下垂控制策略,针对下垂控制存在的鲁棒性能较差及有功功率和无功功率耦合问题,已经提出了各种改进策略.文献[3 ]将连接线路的阻抗角作为变量引入到下垂控制中,添加了一个微分控制环节增加了控制器设计的自由度,并对微电网系统建立降阶模型和全阶模型,通过粒子群算法优化控制参数,较好地提高了微网系统的动态性能.但设计过程中采用的降阶模型需要包含足够多的系统信息,才能满足功率环控制器的设计要求,这对于复杂多变的光储微网控制系统较难将其控制参数精确地反映出来.文献[4 ]考虑了微网系统的线路阻抗对下垂控制的影响,通过增加虚拟阻抗一定程度上改善了系统的控制效果.但在实际应用中,较小的虚拟阻抗难以起到明显的改善效果,过大的虚拟阻抗又会导致电压出现明显跌落,在多数情况下虚拟阻抗为预定值,不能根据系统的变化及时做出调整.文献[5 ]提出了基于本地采样的改进无线互联下垂控制方法,将虚拟阻抗分成两段设计,实现控制器所需电压信号采样点本地化,并且通过增加功率补偿电导和有功功率校正比例,较好地实现了输出功率的精确控制及电压幅值的调节控制.但是该设计仅对系统的静态性能进行分析,在实际应用中必须考虑到系统的动态响应指标进一步完善控制器. ...
Energy management of solar panel and battery system with passive control
1
2007
... 近几年,一些更为先进的非线性控制算法也逐渐应用到光储微电网的控制中,文献[6 ]将无源控制理论应用于微电网中,在此论文中,首先将微电网系统的数学模型写成哈密顿方程,结合哈密顿方程和系统的无源性设计了系统无源控制器,能够较好地实现在弱光照强度下蓄电池放电,强光照情况下蓄电池充电,同时保证直流负载侧电压稳定,系统也具有较好的鲁棒性能,但是所设计的控制器并不能满足系统对控制器有界的要求,这使得在蓄电池在充放电转换过程中会有较大的电压脉冲.文献[7 ]通过建立光储微网的仿射非线性模型,通过无源控制理论验证了光储微网系统的无源性,并采用基于无源性小增益控制策略设计控制器,使得系统满足了对控制器有界的要求,在一定程度上提高了控制性能,但设计过程较为繁琐,控制器需要利用系统中较多参数变量,这使得控制器可实现性较差,且整体控制效果有待进一步提高. ...
基于蓄电池储能的微电网控制系统设计
1
2015
... 近几年,一些更为先进的非线性控制算法也逐渐应用到光储微电网的控制中,文献[6 ]将无源控制理论应用于微电网中,在此论文中,首先将微电网系统的数学模型写成哈密顿方程,结合哈密顿方程和系统的无源性设计了系统无源控制器,能够较好地实现在弱光照强度下蓄电池放电,强光照情况下蓄电池充电,同时保证直流负载侧电压稳定,系统也具有较好的鲁棒性能,但是所设计的控制器并不能满足系统对控制器有界的要求,这使得在蓄电池在充放电转换过程中会有较大的电压脉冲.文献[7 ]通过建立光储微网的仿射非线性模型,通过无源控制理论验证了光储微网系统的无源性,并采用基于无源性小增益控制策略设计控制器,使得系统满足了对控制器有界的要求,在一定程度上提高了控制性能,但设计过程较为繁琐,控制器需要利用系统中较多参数变量,这使得控制器可实现性较差,且整体控制效果有待进一步提高. ...
1
2014
... 基于无源控制(Passivity-based control,PBC)设计作为一种本质上的非线性控制方法[8 ] ,目前在电气控制领域得到了越来越广泛的应用,如文献[9 ]通过建立光伏并网逆变器的EL功率模型,并通过光伏阵列MPPT的最大功率计算出光伏并网逆变器期望最大输出功率,设计了光伏并网逆变器无源功率控制器,得到了非常好的控制效果.基于此,本文将基于EL模型的无源控制策略应用到光储微网系统中,首先分析了双向DC-DC变换器在充、放电时的两种工作状态;其次通过建立光储微网控制系统的EL模型,采用注入阻尼法设计了双向DC-DC变换器无源控制器;最后,通过搭建Simulink仿真模型,验证本文所提出控制策略的正确性和可行性. ...
光伏并网逆变器最大功率传输控制研究
1
2014
... 基于无源控制(Passivity-based control,PBC)设计作为一种本质上的非线性控制方法[8 ] ,目前在电气控制领域得到了越来越广泛的应用,如文献[9 ]通过建立光伏并网逆变器的EL功率模型,并通过光伏阵列MPPT的最大功率计算出光伏并网逆变器期望最大输出功率,设计了光伏并网逆变器无源功率控制器,得到了非常好的控制效果.基于此,本文将基于EL模型的无源控制策略应用到光储微网系统中,首先分析了双向DC-DC变换器在充、放电时的两种工作状态;其次通过建立光储微网控制系统的EL模型,采用注入阻尼法设计了双向DC-DC变换器无源控制器;最后,通过搭建Simulink仿真模型,验证本文所提出控制策略的正确性和可行性. ...
光伏并网逆变器最大功率传输控制研究
1
2014
... 基于无源控制(Passivity-based control,PBC)设计作为一种本质上的非线性控制方法[8 ] ,目前在电气控制领域得到了越来越广泛的应用,如文献[9 ]通过建立光伏并网逆变器的EL功率模型,并通过光伏阵列MPPT的最大功率计算出光伏并网逆变器期望最大输出功率,设计了光伏并网逆变器无源功率控制器,得到了非常好的控制效果.基于此,本文将基于EL模型的无源控制策略应用到光储微网系统中,首先分析了双向DC-DC变换器在充、放电时的两种工作状态;其次通过建立光储微网控制系统的EL模型,采用注入阻尼法设计了双向DC-DC变换器无源控制器;最后,通过搭建Simulink仿真模型,验证本文所提出控制策略的正确性和可行性. ...
A generic battery model for the dynamic simulation of hybrid electric vehicles
1
2007
... 双向DC-DC变换器的主要功能是控制蓄电池的充电和放电,实现控制能量双向流动.在系统运行过程中,通过检测光照强度变化,当光照强度低于设定值时,双向DC-DC变换器工作在Boost状态,蓄电池向负载供能;当光照强度高于设定值时,双向DC-DC变换器工作在Buck状态,将多余的电能存储于蓄电池中,从而保证系统的平稳运行,提高系统安全性和可靠性.在实际应用中,可以根据实际负载的额定功率来配置光伏电池,充分发挥双向DC-DC变换器和蓄电池的能量管理功能,在保证稳定性和可靠性的同时降低系统的配置和运行成本[10 ] . ...
用于电池储能系统的双向DC-DC变换器研究
1
2017
... 双向半桥式DC-DC变换器结构比较简单、元件少,能够高效完成不同状态的快速切换.在实际工程应用中,如果将这种拓扑结构进行串并联组合,可以得到变比和耐压等级更高的双向DC-DC变换器,使得输出的电压纹波和电流纹波更小[11 ] .采用的双向DC-DC变换器结构如图2 所示. ...
1
2012
... 如果存在一个正定函数,$Q(x):{{\mathbf{R}}^{n}}\to R$对$\forall t>0$时所有的$u\in {{\mathbf{R}}^{m}}$和所有的${{x}_{0}}\in {{\mathbf{R}}^{n}}$,得到下列耗散不等式[12 ] ...