1 引言
本文以某高压SF6罐式断路器空载合、分闸操作为研究对象,运用动力学仿真软件建立产品的虚拟样机模型,同时考虑灭弧室压力对零件受力的影响,最终计算与分析了绝缘拉杆在断路器空载合、分闸过程中的动态受力情况。在此基础上,运用有限元分析软件对绝缘拉杆进行静力学与瞬态动力学仿真分析,校核绝缘拉杆在合、分闸操作过程中的强度,并提出改善绝缘拉杆受力状况与提高安全系数的相关建议。本文提供了一种绝缘拉杆从受力分析到强度校核完整的仿真分析方法,该方法还可以推广到开关产品其他零部件的受力分析与强度校核上去,具有很强的实用价值。
2 绝缘拉杆受力分析
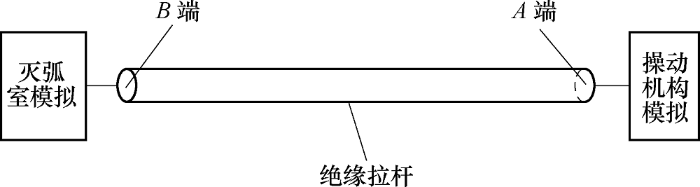
图1
2.1 动力学仿真模型的建立
ADAMS软件是目前世界范围内使用最广泛的机械系统动力学仿真分析软件之一,它为用户提供了一个集建模、求解、可视化技术于一体的虚拟样机环境。它可以方便地建立参数化的实体模型,该模型可以是在ADAMS软件中直接建立的简单模型,也可以是从其它三维造型软件中导出的复杂几何模型。然后在模型上施加力或力矩、运动副和激励,最后采用多体系统动力学原理,通过建立多体系统的运动方程和动力学方程进行求解计算,方程的建立和求解都是由软件自动完成,无需用户编程,这就使用户从繁琐的编程中解脱出来,从而能够将主要精力放在所关心的问题上。
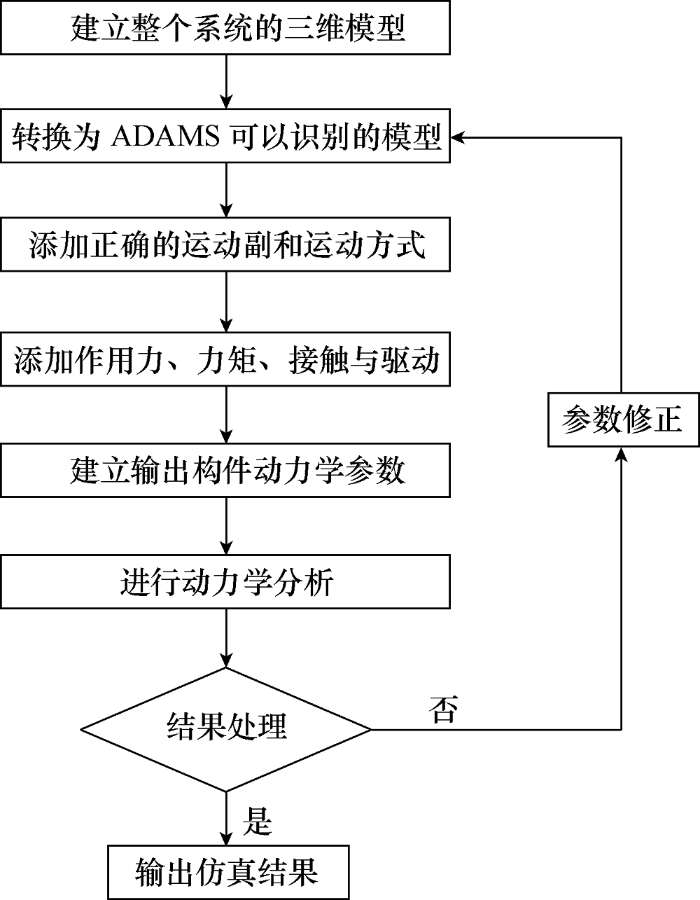
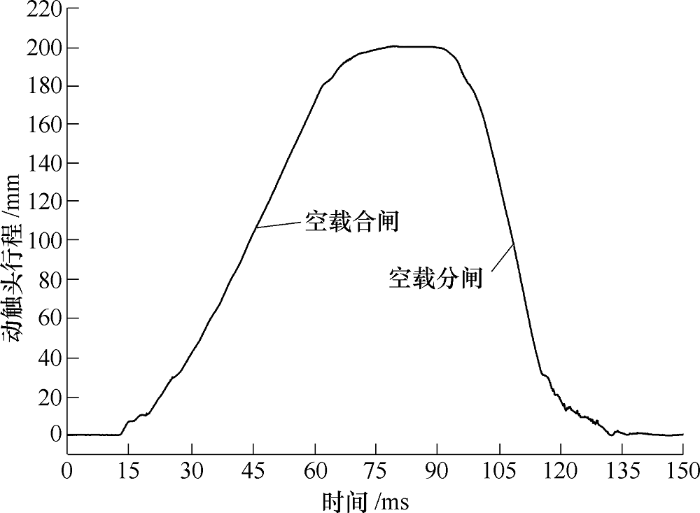
动力学分析的基本步骤如图2所示。为了简化仿真模型与减少计算量,在保证能对绝缘拉杆正确受力分析的前提下,可以将图1所示的操动机构模拟部分用试验得到的空载合、分闸特性曲线代替,即在直动密封杆一端(与操动机构相连侧)添加如图3所示的断路器空载合、分闸特性实测曲线作为驱动条件,继而省略掉操动机构部分。整个动力学建模过程可描述为:利用相关软件对断路器进行三维实体建模与简化处理,然后把三维实体模型转换为ADAMS可以识别的数据,将模型导入ADAMS中,再根据实际设计要求,给各个零件添加正确的约束副、力、力矩和初始条件,并把动弧触头与静主触头等相关零件转化为柔性体,以图3所示的空载合、分闸特性实测曲线作为驱动添加在直动密封杆上,最终就能建立断路器的虚拟样机模型。
图2
图3
2.2 压气室气体压力数学模型
灭弧室第Ⅰ部分气体是变质量系统,利用变质量系统的热力学第一定律与气体状态方程,获得压气缸中气体温度的变化率
式中,${{C}_{v}}$为SF6气体定容比热容;${{m}_{l}}$为压气室内气体质量;$R$为气体常数;${{T}_{l}}$为系统中SF6气体的绝对温度;${{p}_{l}}$为压气室内任一时刻气体压力;${{A}_{l}}$为压气室压力作用面积。
压气室内任意时刻气体压力${{p}_{l}}$可由比较准确而实用的Beattie-Bridgman气体状态方程表达
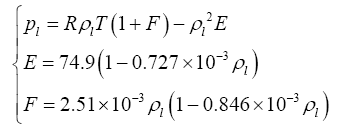
式中,${{\rho }_{l}}$为压气室内气体密度。
将灭弧室触头空载分闸过程分为三个阶段,即预压缩阶段、喷口喉部堵塞阶段、气吹阶段。由式(2)可知,为求各阶段压气室内气体压力,需先分别计算出该阶段压气室内气体的温度和密度。压气室气体温度可以用式(1)来求解,密度与质量流量存在如下关系。
式中,${{m}_{0}}$为压气室SF6气体初始质量;${{G}_{l}}$为压气室流向喷口外部气体的质量流量;${{V}_{0}}$为压气室内气体初始体积。
气吹阶段压气室流出气体质量流量可以用下式表示[20]
式中,${{A}_{d}}$为动弧触头横截面积;${{A}_{p}}$为喷口喉部面积;${{C}_{p}}$为SF6气体定压比热容;${{p}_{0}}$为压气室气体初始压力。而预压缩阶段与喷口喉部堵塞阶段的气体质量流量表达式与气吹阶段相似,可参考式(4)获得。
2.3 绝缘拉杆受力分析
通过以上虚拟样机模型的建立与仿真分析,可以方便给出绝缘拉杆两端的受力情况。为了分析方便,以下仅给出绝缘拉杆A端(与机构侧相连)沿轴向方向的受力情况。
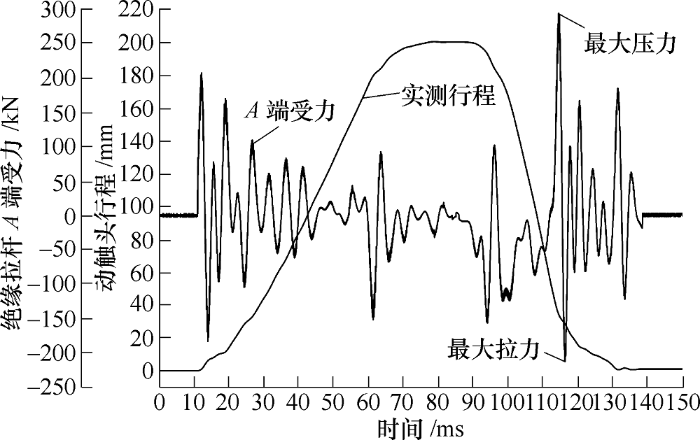
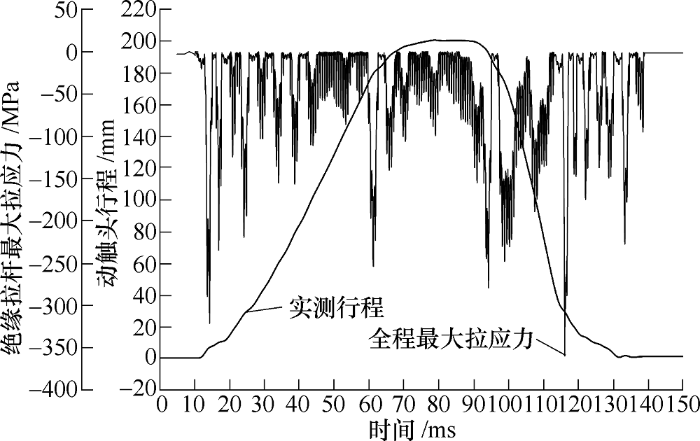
图4给出了绝缘拉杆A端在断路器空载合、分闸操作过程中沿轴线方向受力情况,规定当受力方向沿轴向(Y轴)正方向时,用正值表示,表示绝缘拉杆A端此时受压;当受力方向沿轴向(Y轴)负方向时,用负值表示,表示绝缘拉杆A端此时受拉。从图4中可以看出,绝缘拉杆A端在整个空载合、分闸操作过程中,所受的最大压力为294.8 kN,所受的最大拉力为213.0 kN。从图4中还可以看出,在断路器空载合、分闸过程中绝缘拉杆A端受力波动很大。结合行程曲线可以看出,在行程曲线的波动较大处(不光滑处),A端受到的冲击力较大。由于空载分闸速度高,当断路器刚进入到分闸缓冲时,行程曲线具有较大的波动,此时绝缘拉杆A端所受冲击力最大。因此可以肯定:改善空载合、分闸时的缓冲性能,不仅可以使行程曲线变得更光滑(波动变小),也能减小绝缘拉杆的受力。但即使在原有缓冲情况下,绝缘拉杆A端所受到的最大拉力不仅远小于破坏拉力(≥430kN),也小于例行拉力(≥220kN),即绝缘拉杆的受力是满足技术要求的。
图4
根据绝缘拉杆所受的最大拉力(213.0 kN)与横截面积,可以采用下式粗略计算绝缘拉杆的最大拉应力(由于绝缘拉杆具有优秀的抗压性能,故以下应力的校核主要针对拉应力)
式中,$\sigma $为绝缘拉杆端部受到的应力;${{F}_{\max }}$为绝缘拉杆受到的最大拉力;$A$为绝缘拉杆端部横截面积;$R$为绝缘拉杆端部外半径;$r$为绝缘拉杆端部内半径。
利用式(5)获得的绝缘拉杆最大拉应力$\sigma \text{=}$ $\text{175}\text{.24 MPa}$,同时依据表1给出的绝缘拉杆抗拉强度${{\sigma }_{b}}=560\ \text{MPa}$,获得该绝缘拉杆此时的安全系数
3 绝缘拉杆静力学分析
静力学分析是有限元分析中最简单、同时也是最基础的分析方法,一般工程计算中最经常应用的分析方法就是静力学分析。静力学分析的步骤包括:几何建模(外部几何数据的导入)、材料赋予、网格设置与划分、施加载荷和边界条件、问题求解、结果后处理[21]。
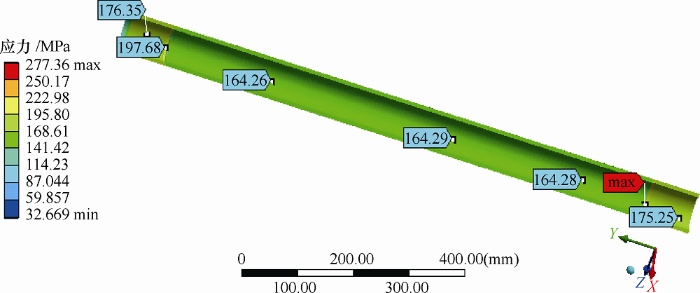
图5
图6
4 绝缘拉杆瞬态动力学分析
瞬态动力学分析亦称时间历程分析,是分析结构在随时间任意变化的载荷作用下动力响应过程的一种方法。利用瞬态动力学分析可以确定结构在瞬态载荷(时间函数的载荷)作用下随时间变化的位移、应变以及应力等。瞬态动力学分析包括线性瞬态动力学分析和非线性瞬态动力学分析两种分析类型。所谓线性瞬态动力学分析,是指模型中不包括任何非线性行为,适用于线性材料、小位移、小应变、刚度不变结构的瞬态动力学分析,其算法有两种:直接法和模态叠加法。非线性瞬态动力学分析可以考虑各种非线性行为,如材料非线性、大变形、大位移、接触、碰撞等,其算法主要有隐式算法和显示算法两种。本节将采用线性直接算法对绝缘拉 杆进行瞬态动力学分析。
利用ANSYS Workbench软件对绝缘拉杆进行瞬态动力学分析的步骤包括:① 建立有限元模型,设置材料特性;② 定义接触区域(如果有接触的话);③ 定义网格控制并划分网格;④ 施加载荷和边界条件;⑤ 定义分析类型;⑥ 设置求解选项;⑦ 对问题进行求解;⑧ 进行结果评价和分析。
本节将利用第1节获得的绝缘拉杆A端随时间变化的瞬态载荷,通过ANSYS Workbench 软件对绝缘拉杆进行瞬态动力学分析,得到绝缘拉杆在断路器空载合、分闸操作下随时间变化的应力。
4.1 网格划分
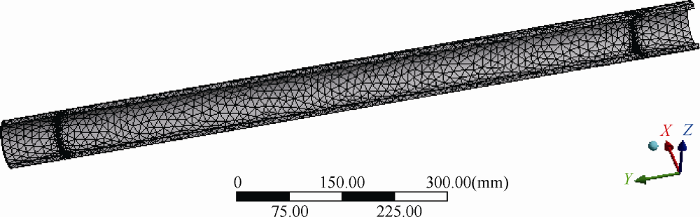
在Transient Structural模块下,对绝缘拉杆模型进行网格划分,如图7所示。网格划分后的节点数为30 090个,单元数为16 355个。
图7
4.2 瞬态动力学分析结果
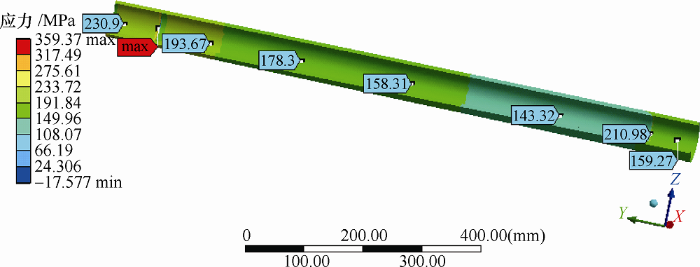
图8
图9
由于绝缘拉杆是脆性材料,而脆性材料的均匀性较差,且存在突然断裂的风险,相对于塑性材料,其安全系数取值较大,一般取$S=2.0~3.5$[22]。但由式(8)可知,按照瞬态动力学结果计算获得的安全系数小于2,安全系数偏低。为提高安全系数,在绝缘拉杆结构不变的前提下,需通过改善绝缘拉杆的受力情况来实现。
5 受力改善建议
依据以上绝缘拉杆受力分析与强度校核分析结果,为了改善绝缘拉杆在断路器空载合、分闸操作过程的受力情况与提高安全系数,在绝缘拉杆结构不变的前提下,有如下改善建议。
(1) 建议改善空载合闸启动阶段的波动与分闸缓冲段的缓冲性能,尽量使行程曲线变得更加光滑,从而减少空载合、分闸过程中绝缘拉杆所受到的冲击力;
(2) 建议更改退刀槽形状,可以考虑将直角过渡变为圆角过渡,减少退刀槽处的应力集中;
(3) 在可能的情况下,建议绝缘拉杆与接头直接用胶粘接,避免退刀槽的出现。
6 结论
本文以高压SF6罐式断路器样机为研究对象,运用动力学仿真软件建立断路器的虚拟样机模型,同时考虑灭弧室压力对零件受力的影响,最终计算出了绝缘拉杆在断路器空载合、分闸过程中的动态受力情况。受力分析结果显示:绝缘拉杆受到较大的冲击载荷,但最大冲击拉力低于破坏拉力。其次在绝缘拉杆受力分析的基础上,运用ANSYS Workbench软件对绝缘拉杆进行静力学与瞬态动力学仿真分析,校核绝缘拉杆在合、分闸操作过程中的强度。强度校核结果显示:采用静力学与瞬态动力学计算获得的绝缘拉杆最大拉应力均低于材料的抗拉强度,绝缘拉杆能够满足拉伸强度要求,但按照瞬态动力学计算得到的安全系数偏低。最后为改善绝缘拉杆受力状况与提高安全系数,提出了相应的改进建议。该研究提供了一种产品零部件受力分析与强度校核的方法,可以用来提高产品设计质量,缩短产品开发周期,降低产品设计成本。
参考文献
断路器绝缘拉杆的动力学仿真分析与试验研究
[J].
Dynamics simulation analysis and experimental study of circuit-breaker’s insulation pull rod
[J].
一起550 kV瓷柱式断路器绝缘拉杆的事故分析
[J].
Analysis on an accident of insulated pull rod of 550 kV porcelain column circuit breaker
[J].
高压电器中绝缘拉杆的瞬态动力学分析
[J].
Analysis of transient dynamics of the insulation pull rod in high voltage apparatus
[J].
断路器绝缘拉杆的可靠性验证
[J].
The reliability verification of the insulation pull rod in circuit breaker
[J].
SF6高压断路器分合闸绝缘拉杆动态形变的测试分析
[J].
Measurement and analysis of dynamic deformation of SF6 circuit breaker’s insulated pull rod for on-off operation
[J].
绝缘拉杆拉力试验装置
[J].
The insulation pull rod tension test device
[J].
基于UG和ADAMS的高压开关弹簧机构动力学仿真和优化
[J].
Kinematic simulation and optimization for spring operating mechanism of circuit switch based on UG and ADAMS
[J].
高压开关传动系统的运动学与动力学仿真
[J].
Kinematic and dynamic simulations of drive systems of high-voltage switchgears
[J].
高压断路器运动特性仿真
[J].
The moving characteristic simulation of high voltage circuit breaker
[J].
弹簧机构输出与灭弧室触头运动映射关系分析
[J].
Analysis of the mapping connection between spring mechanism output and the interrupter contacts
[J].
压气式SF6断路器灭弧室与操动机构行程特性仿真方法研究
[J].
Simulation method for arc quenching chamber and operation mechanism displacement characteristics of SF6 puffer circuit breaker
[J].
252 kV SF6断路器空载时压力特性试验研究
[J].
Experimental research on pressure characteristic of 252 kV SF6 circuit breaker without load
[J].
弹簧操动机构用缓冲器流场仿真与强度分析
[J].
Flow field simulation and oil cylinder strength analysis on hydraulic buffer of spring operating mechanism
[J].