电气工程学报, 2019, 14(2): 86-91 doi: 10.11985/2019.02.015

配电网中谐波传递特性研究 *

安海清1, 岳娜1, 李振动1, 金海望1, 田凯哲1, 李金卜1, 华回春1

1. 国网冀北电力有限公司检修分公司 北京 102488

2. 华北电力大学数理学院 保定 071003

Research on Harmonic Transfer Characteristics in Distribution Network

AN Haiqing1, YUE Na1, LI Zhendong1, JIN Haiwang1, TIAN Kaizhe1, LI Jinbo1, HUA Huichun1

1. State Grid Jibei Electric Power Company Limited Maintenance Branch Company, Beijing 102488 China

2. School of Mathematics and Physics，North China Electric Power University, Baoding 071003 China

收稿日期: 2019-03-21   网络出版日期: 2019-06-25

基金资助: * 中央高校基本科研业务费专项资金资助项目.  2017MS197

Received: 2019-03-21   Online: 2019-06-25

作者简介 About authors

安海清,男,1990年生,工程师。主要研究方向为电能质量分析与控制等。E-mail：245932206@qq.com。

岳娜,女,1989年生,工程师。主要研究方向为电能质量分析与控制等。

摘要

从谐波电流和谐波电压两个方面研究了谐波在配电网中的传递特性,通过公式推导分析了谐波电流在相同和不同电压等级系统中的传递规律。在未投入滤波装置时,谐波电流主要流入上级系统;而当谐波电流注入上级系统后,从低压侧向高压侧传递时,传递系数与变压器电压比有关。详细分析了上级电网谐波电压向本级电网负荷侧的传递过程,结果表明上级电网的谐波电压在配电网中传递时主要集中在本级电网的负荷等效阻抗上;投入滤波器后,上级电网的谐波电压传递主要集中在本级电网的系统阻抗上。最后通过算例仿真验证了结论的准确性。

关键词： 配电网 ; 谐波电流 ; 谐波电压 ; 谐波传递特性 ; 滤波器

Abstract

The harmonic transfer characteristics in the distribution network are analyzed from two aspects of harmonic current and harmonic voltage. The transfer law of harmonic current in the same and different voltage level systems is analyzed by formula. The analysis results show that the harmonic current mainly flows into the upper system when the filter device is not input. The transmission coefficient is related to the transformer ratio when the wave current is injected into the upper system and transmitted from the low pressure side to the high pressure. The transmission process of the harmonic voltage of the upper power grid to the load side of the power grid is analyzed in detail and the conclusion is drawn. The harmonic voltage of the higher-level power grid is mainly concentrated on the load equivalent impedance of the current-level power grid when passing through the distribution network. When the harmonic filter voltage of the upper-level power grid is mainly transmitted, the system is mainly concentrated on the system of the current-level power grid. The accuracy of the conclusions is verified by numerical simulation.

Keywords： Distribution network ; harmonic current ; harmonic voltage ; harmonic transfer characteristics ; filter

PDF (411KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

安海清, 岳娜, 李振动, 金海望, 田凯哲, 李金卜, 华回春. 配电网中谐波传递特性研究 *. 电气工程学报[J], 2019, 14(2): 86-91 doi:10.11985/2019.02.015

AN Haiqing. Research on Harmonic Transfer Characteristics in Distribution Network. Journal of Electrical Engineering[J], 2019, 14(2): 86-91 doi:10.11985/2019.02.015

1 引言

随着全球能源互联网战略的提出,分布式新能源发电技术[1,2,3]、柔性直流输电技术[4,5]等获得了快速的发展。其中,分布式光伏发电因为能效利用合理、污染少、运行灵活、经济性好等特点被越来越多地接入到配电网中,然而其中电力电子元器件的大量使用也给配电网带来了较为严重的谐波问题[6,7]。

目前,国内外对谐波问题的研究主要集中在对谐波进行检测[8]、谐波源定位[9]、谐波责任划分等[10,11,12],而对谐波在配电网中的传递特性研究较少[13,14,15]。由于电网拓扑结构的不同导致电网结构参数差异较大,因而谐波在电网中的传播机理也错综复杂。因此研究谐波在电网中的传递特性,理清谐波的传递规律有助于更好地对谐波进行治理。

在现有的谐波传递问题研究中,文献[13]在定义了谐波电压传递系数的基础上,得出谐波电压从高压向低压传递时具有较强的渗透能力;而从低压向高压传递时,穿透能力不强;同电压等级之间传播与距离有关的结论。文献[14]研究了谐波在变压器之间的传递特性,并指出当变压器轻载时,电源侧谐波在变压器中是线性传递的。文献[15]主要对高压直流输电中的谐波传递特性进行了研究,并通过数学运算推导得出谐波从交流侧到直流侧的传递规律,但并未对谐波在交流电网中的传递特性进行说明。

本文主要研究谐波在配电网中的传递特性,并从谐波电流和谐波电压两个方面进行了分析,争取填补了目前这一研究方向的空白。

2 配电网中谐波电流的传递特性

2.1 同一电压等级系统内的传递特性

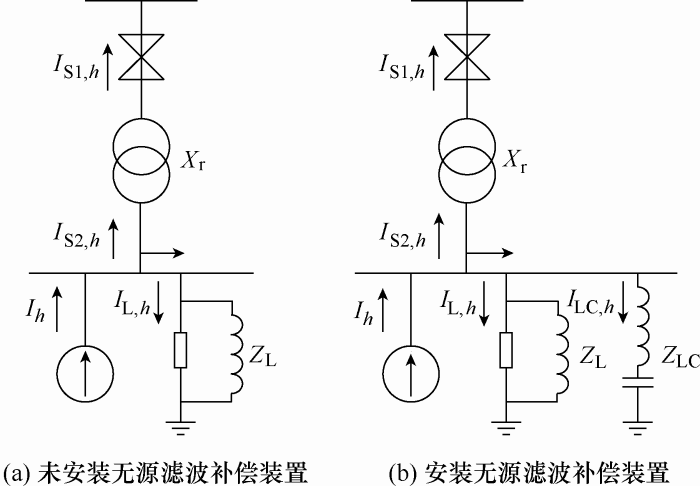
如图1a所示,当配电网中未装设滤波装置时,非线性负荷产生的谐波电流$\dot{I}_{h}$ (h表示谐波次数),一部分流入上级系统,一部分流入本地负荷,且满足如下关系

$\dot{I}_{h}=\dot{I}_{S2,h}+\dot{I}_{L,h}$

式(1)中,注入上级系统的谐波电流$\dot{I}_{S2,h}$与注入本地负荷的谐波电流$\dot{I}_{L,h}$大小与系统等效谐波阻抗$X_{S2,h}$和负荷的等效谐波阻抗$Z_{L,h}$有关,即

${{\dot{I}}_{\text{S2},h}}=\left| \frac{{{Z}_{\text{L},h}}}{{{Z}_{\text{L},h}}+\text{j}{{X}_{\text{S2,}h}}} \right|{{\dot{I}}_{h}}$
${{\dot{I}}_{\text{L},h}}=\left| \frac{\text{j}{{X}_{\text{S2,}h}}}{{{Z}_{\text{L},h}}+\text{j}{{X}_{\text{S2,}h}}} \right|{{\dot{I}}_{h}}$

在配电系统中,由于$\left| {{Z}_{\text{L},h}} \right|\gg {{X}_{\text{S2,}h}}$,则有${{\dot{I}}_{\text{S2},h}}\approx {{\dot{I}}_{h}}$。因此,对于不含谐波滤波装置的配电网,非线性负荷产生的谐波电流主要流入上级系统中,并在系统等效谐波阻抗上产生谐波电压。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   谐波电流在配电网中的传递示意图


当配电网供电母线上安装谐波滤波装置时,如图1b所示,非线性负荷产生的谐波电流${{\dot{I}}_{h}}$,大部分流入了谐波滤波器${{\dot{I}}_{\text{LC,}h}}$,另一部分则流入了上级系统${{\dot{I}}_{\text{S2,}h}}$和本地其他的负荷馈线${{\dot{I}}_{\text{L,}h}}$,且满足如下关系

${{\dot{I}}_{h}}={{\dot{I}}_{\text{S2},h}}+{{\dot{I}}_{\text{L},h}}+{{\dot{I}}_{\text{LC},h}}$

注入滤波器、上级系统及本地负荷馈线的谐波电流大小,也与各条支路的等效谐波阻抗有关,与式(2)、(3)的分流原理相同,不再赘述。

由于无源滤波器的工作原理是对需要滤除的谐波电流呈现低阻抗,使谐波电流主要流入谐波滤波器支路中,减小注入上级系统的谐波电流值,从而达到滤除谐波的目的。但实际情况中,无源滤波器的滤波能力有限,只能滤除大部分的低次谐波。

2.2 不同电压等级系统内的传递特性

非线性负载产生的谐波电流注入上级系统后,需要从变压器低压侧向高压侧传递,其传递系数kIh与变压器两端的电压变比N有关,即

${{k}_{Ih}}=\frac{{{{\dot{I}}}_{\text{S1},h}}}{{{{\dot{I}}}_{\text{S2},h}}}=\frac{{{U}_{2}}}{{{U}_{1}}}=\frac{1}{N}$

将式(5)变换形式得

${{\dot{I}}_{\text{S1},h}}={{k}_{Ih}}{{\dot{I}}_{\text{S2},h}}=\frac{{{{\dot{I}}}_{\text{S2},h}}}{N}$

可见,变压器低压侧的谐波电流向高压侧传递时,谐波电流会变小。但上述关系只适用于具有正序和负序特性的谐波电流,对于零序谐波电流,由于其流通路径与变压器的接法有关,因此并不满足式(5)和式(6)。

3 配电网中谐波电压的传递特性

对于某个具体的用户而言,谐波电压主要包括两个方面：一方面来自上级电网谐波电压的渗透,另一方面来自本级电网其他电力用户在系统谐波阻抗上产生的谐波电压。本级电网其他电力用户在系统谐波阻抗上产生的谐波电压向上级系统的传递特性已述,在此主要分析上级电网谐波电压向本级电网负荷侧的传递过程。

3.1 传递原理

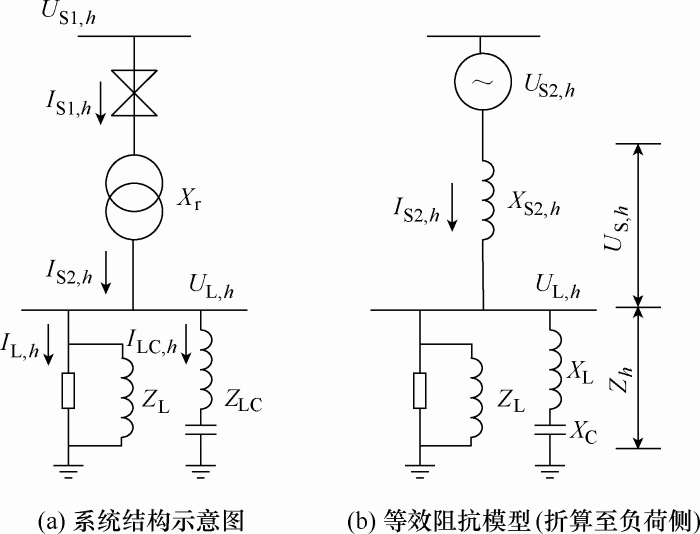
图2为上级系统谐波电压向本级电网负荷侧传递的示意图。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   上级电网谐波电压向负荷侧传递示意图


上级电网的谐波电压${{\dot{U}}_{\text{S1,}h}}$传递到本级电网负荷侧供电母线时,与本级电网的系统等效谐波阻抗${{X}_{\text{S2,}h}}$、广义负荷等效谐波阻抗${{Z}_{h}}$以及变压器的电压比N有关,即

${{U}_{\text{L,}h}}=\left| \frac{{{Z}_{h}}}{\text{j}{{X}_{\text{S2,}h}}+{{Z}_{h}}} \right|\frac{{{U}_{\text{S1,}h}}}{N}=\left| \frac{{{Z}_{h}}}{\text{j}{{X}_{\text{S2,}h}}+{{Z}_{h}}} \right|{{U}_{\text{S2,}h}}$

如果用高压侧的谐波电压含有率表示,则

$HR{{U}_{\text{L,}h}}=\left| \frac{{{Z}_{h}}}{\text{j}{{X}_{\text{S2,}h}}+{{Z}_{h}}} \right|HR{{U}_{\text{S1},h}}$

3.2 负荷侧未安装滤波器的传递特性分析

若负荷侧未安装滤波器时,负荷等效谐波阻抗${{Z}_{h}}={{Z}_{\text{L},h}}$,其中${{Z}_{\text{L},h}}$为用电负荷的等效谐波阻抗。

一般在配电网中,由于$\left| {{Z}_{\text{L},h}} \right|\gg {{X}_{\text{S2,}h}}$,所以上级电网传递至负荷侧的谐波电压大部分分压在负荷等效谐波阻抗上。而根据工程经验,一般情况下都有${{U}_{\text{L,}h}}\approx (0.6\tilde{\ }1.0){{U}_{\text{S2,}h}}$。需要注意的是,由于系统阻抗以感性为主,而负载阻抗一般呈阻感性且以阻性为主,因此随着谐波次数的增加,负荷阻抗分压比例会逐渐降低。

由上级电网谐波电压在负荷侧引起的谐波电电流为

${{I}_{\text{S2,}h}}=\frac{{{U}_{\text{S,}h}}}{{{X}_{\text{S,}h}}}=\frac{{{U}_{\text{L,}h}}}{{{Z}_{\text{L,}h}}}$

由于负荷等效阻抗一般较大,因此上级电网的谐波电压在本地负荷阻抗上产生的谐波电流一般很小。

3.3 负荷侧安装滤波器的传递特性分析

将无源滤波器作为广义负荷,此时,负荷的等效阻抗${{Z}_{h}}={{Z}_{\text{L},h}}\parallel {{Z}_{\text{LC},h}}$,其中,${{Z}_{\text{LC},h}}$为并联的无源滤波支路的等效谐波阻抗。当${{Z}_{\text{L},h}}\gg {{Z}_{\text{LC},h}}$时,${{Z}_{h}}\approx {{Z}_{\text{LC},h}}$,则式(7)可以简化为

${{U}_{\text{L,}h}}=\left| \frac{{{Z}_{\text{LC,}h}}}{\text{j}{{X}_{\text{S2,}h}}+{{Z}_{h}}} \right|{{U}_{\text{S2,}h}}={{k}_{Uh}}{{U}_{\text{S2,}h}}$

分析式(10),可得出以下结论。

(1) 当无源滤波器的电抗和电容发生串联谐振时,其等效谐波阻抗${{Z}_{\text{LC},h}}$较小,从而${{k}_{Uh}}$很小,因此相应频率的上级电网谐波电压主要分压在负荷侧系统阻抗上,而传递至负荷供电母线上的谐波电压分量较小。

(2) 当无源滤波器和系统发生串联谐振时,即${{Z}_{\text{LC},h}}+\text{j}{{X}_{\text{S,}h}}$阻抗很小,此时${{k}_{Uh}}$很大,使对应频率的上级电网谐波电压在传递至本地负荷侧供电母线时产生了放大效应,使其远大于上级电网谐波电压值。

(3) 另外,其他频率的谐波电压传递时需要将负荷等效谐波阻抗和无源滤波器的等效谐波阻抗并联后与系统等效谐波阻抗进行分压,分析方法与前面类似,在此不再赘述。

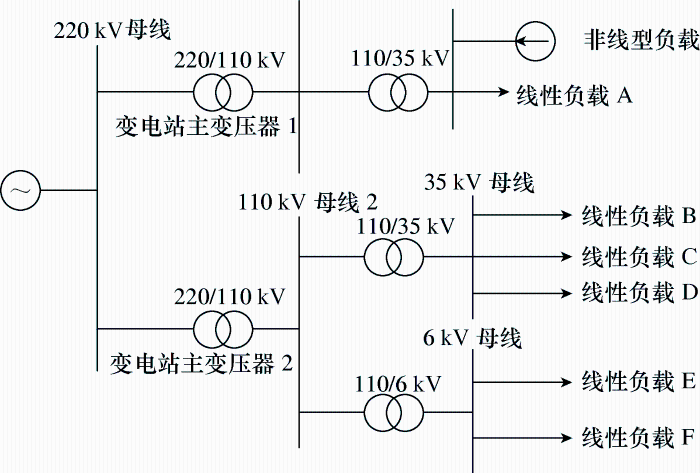
4 仿真验证

图3为本文验证谐波传递特性的仿真测试系统示意图。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   仿真测试系统示意图


4.1 同一电压等级谐波电流的传递

记非线性负载注入的谐波电流有效值为${{I}_{h}}$,注入系统的谐波电流有效值为${{I}_{\text{S2,}h}}$,注入负荷的谐波电流有效值为${{I}_{\text{L,}h}}$。表1为配电网未安装滤波装置情况下${{I}_{h}}$、${{I}_{\text{S2,}h}}$和${{I}_{\text{L,}h}}$的2~7次谐波电流有效值。

表1   谐波电流有效值

谐波次数h${{I}_{h}}$/A${{I}_{\text{S2,}h}}$/A${{I}_{\text{L,}h}}$/A.
235.14335.1400.14
335.11135.1070.21
435.17435.1710.283
535.06635.0660.354
634.46434.4630.418
732.73532.7350.465

新窗口打开| 下载CSV


由表1中数据分析可知,当配电网中未安装滤波装置时,非线性负载产生的谐波电流几乎全部流入上级系统,而流入本地负荷的谐波电流很少。验证了上述结论：对于不含谐波滤波装置的配电网,非线性负荷产生的谐波电流主要流入上级系统。

下面在负荷侧添加滤波器,品质因数设为60,主要消除5次谐波。${{I}_{h}}$、${{I}_{\text{S2,}h}}$、${{I}_{\text{L,}h}}$的2~7次谐波有效值见表2。

表2   谐波电流有效值

谐波次数h${{I}_{h}}$/A${{I}_{\text{S2,}h}}$/A${{I}_{\text{L,}h}}$/A
235.14316.3970.066
335.1114.0460.026
435.1741.2040.01
535.0661.1280.003
634.4640.6710.008
732.7351.2490.014

新窗口打开| 下载CSV


表2相比表1而言,注入系统和注入负荷的谐波电流明显减小,大部分的谐波电流流入滤波器中,可见滤波器的工作原理是对需要滤除的谐波电流呈现低阻抗,使谐波电流主要流入谐波滤波器支路中,减小注入系统的谐波电流值,从而达到滤除谐波的目的。

4.2 不同电压等级间谐波电流的传递

本文通过从变压器二次低压侧向一次高压侧传递的算例仿真来验证谐波电流在不同电压等级之间的传递特性。变压器的联结组别分别为$\text{Ynd}$、$\text{Yny}$、$\text{Yy}$、$\text{Yyn}$、$\text{Yd}$、$\text{Dyn}$、$\text{YnYn}$、$\text{Dd}$、$\text{Dy}$时,谐波源负荷注入的正序和负序谐波电流都满足式(5)和式(6)。变压器电压比N为3.143。

表3为谐波电流有效值,可以看出,计算结果符合式(5)和式(6)的结论。

表3   谐波电流有效值

谐波次数h${{I}_{h}}$/A${{I}_{\text{S2,}h}}$/A${{I}_{\text{S1,}h}}$/A${{I}_{\text{S2,}h}}$/${{I}_{\text{S1,}h}}$
235.14335.1411.1713.146
335.11135.10711.1593.146
435.17435.17111.1823.145
535.06635.06611.1753.138
634.46434.46310.9943.135
732.73532.73510.4463.134

新窗口打开| 下载CSV


当谐波负荷注入零序谐波电流且绕组为星形联结时,零序电流不能流通,此时等效电路在这一边应该断开;如果绕组为三角形联结,则零序电流仅能够在三角形内部短接,而不会流到外电路去,即在零序等效电路中,相当于变压器内部短接,但从外部看进去是开路的,下面进行仿真验证。

由于变压器高低压侧为星形联结或三角形联结的情况相似,下面仅以联结组别为$\text{Ynd}$的情况予以说明,见表4。

表4   谐波电流有效值

谐波次数hIh/A IS2,h/A IS1,h/A IL,h/A
235.1431.94×10-104.362×10-1135.143
335.1110.0010.000 335.111
435.1749.83×10-111.856×10-1135.174
535.0660.0010.000 335.066
634.4648.906×10-111.489×10-1134.464
732.7350.0010.000 332.734

新窗口打开| 下载CSV


从表4可以看出,在该联结组别下,零序电流不能够通过变压器流入系统,所以大部分谐波电流都流入了负荷。另外,当变压器两侧都为星形接地形式时,零序谐波电流是可以流通的,表5为变压器$\text{YnYn}$联结时零序谐波电流的传递情况。

表5   谐波电流有效值

谐波次数hIh/A IS2,h/A IS1,h/A IL,h/A
235.14335.1411.1810.14
335.11135.10711.1710.21
435.17435.17111.1910.283
535.06635.06611.1570.353
634.46434.46310.9660.418
732.73532.73410.4160.465

新窗口打开| 下载CSV


4.3 负荷侧未安装滤波器谐波电压的传递

表6为通过算例仿真验证的未安装无源滤波装置时${{U}_{\text{S2,}h}}$和${{U}_{\text{L,}h}}$的有效值,此时的谐波电流来自上级电网而非负荷侧。

表6   谐波电压有效值

谐波次数hUS2,h/ kV UL,h/ kV UL,h/US2,h
20.5290.5090.962
30.780.7280.93
41.0270.9160.89
51.2411.060.85
61.4411.1590.8
71.5731.1890.756

新窗口打开| 下载CSV


从仿真结果可以看出,上级电网的谐波电压传至负荷侧的谐波电压主要集中于负荷等效谐波阻抗上,而且${{U}_{\text{L,}h}}$/${{U}_{\text{S2,}h}}$的比值也符合工程经验的要求,且在0.6~1.0范围内随着谐波次数的增减逐渐减小。算例仿真结果很好地验证了上述分析和结论。

4.4 负荷侧安装滤波器谐波电压的传递

下面通过仿真结果验证本文第3.3节的结论(1)。当在负荷侧接入滤波器且在3次谐波附近发生串联谐振时,测量得到的${{U}_{\text{S2,}h}}$和${{U}_{\text{L,}h}}$的有效值见表7。

表7   谐波电压有效值

谐波次数hUS2,h/ kV UL,h/ kV US2,h/ UL,h
20.380.1532.484
30.6290.02228.591
40.8630.07511.507
51.0760.1397.741
61.2730.187.072
71.4190.2116.725

新窗口打开| 下载CSV


从表7可以看出,负荷侧供电母线的3次谐波电压${{U}_{\text{L,}h}}$比${{U}_{\text{S2,}h}}$小很多,后者是前者的近29倍,所以算例仿真验证了结论：当滤波器的电抗和电容发生串联谐振时,其等效谐波阻抗${{Z}_{\text{LC},h}}$较小,${{k}_{Uh}}$很小,因此相应频率的背景谐波电压主要分压在负荷侧系统阻抗上,而传递至负荷供电母线上的谐波电压分量很小。

下面通过仿真结果验证本文第3.3节的结论(2)。仿真算例中,令${{Z}_{\text{LC},h}}$与${{X}_{\text{S,}h}}$在3次谐波频率处发生串联谐振。在仿真系统中测量得到的${{U}_{\text{S2,}h}}$及${{U}_{\text{L,}h}}$见表8。

表8   谐波电压有效值

谐波次数hUS2,h/ kV UL,h/ kV UL,h/ US2,h
20.7081.2721.8
30.0952.6527.895
40.6520.8091.241
50.9250.5080.549
61.1490.3730.325
71.3080.2720.208

新窗口打开| 下载CSV


从表8可以看出,负荷侧供电母线电压${{U}_{\text{L,}h}}$在3次谐波频率处远远大于上级系统的谐波电压${{U}_{\text{S2,}h}}$,近于28倍,发生了谐波放大,所以验证了结论：当滤波器和系统阻抗发生串联谐振时,对应频率的上级系统谐波电压在传递至负荷侧供电母线时产生了放大。

5 结论

本文对配电网中的谐波传递特性进行了研究,主要从谐波电流和谐波电压两个方面进行传递特性分析,并通过算例仿真验证了如下结论。

(1) 对于不含谐波滤波装置的配电网,非线性负荷产生的谐波电流主要流入上级系统中,并在系统等效谐波阻抗上产生谐波电压。当谐波电流从变压器低压侧向高压侧传递时,谐波电流传递系数与变压器电压比有关。此外,变压器联结组别的不同也会影响到零序谐波电压在变压器间的传递特性。

(2) 上级电网的谐波电压传至本地负荷侧的谐波电压主要集中于负荷等效谐波阻抗上,且${{U}_{\text{L,}h}}$/${{U}_{\text{S2,}h}}$的比值在0.6~1.0范围之内,并随着谐波次数的增减逐渐减小。接入滤波器后,上级电网的谐波电压主要传递到负荷侧系统阻抗上,甚至有可能会产生放大效应,而传递至负荷供电母线上的谐波电压分量较小。

参考文献

曹炜, 徐永海, 王亚奇 .

不对称故障条件下并网光伏逆变器功率波动与电流抑制改进控制策略

[J]. 现代电力, 2017,34(5):82-88.

[本文引用: 1]

Cao Wei, Xu Yonghai, Wang Yaqi .

An improved control strategy of power fluctuation and current suppression grid-connected photovoltaic inverter under unbalanced fault condition

[J]. Modern Electric Power, 2017,34(5):82-88.

[本文引用: 1]

谢东 .

分布式发电多逆变器并网孤岛检测技术研究

[D]. 合肥:合肥工业大学, 2014.

[本文引用: 1]

蓝澜 .

新能源发电特性与经济性分析研究

[D]. 北京:华北电力大学, 2014.

[本文引用: 1]

贺之渊, 刘栋, 庞辉 .

柔性直流与直流电网仿真技术研究

[J]. 电网技术, 2018,42(1):1-12.

[本文引用: 1]

He Zhiyuan, Liu Dong, Pang Hui .

Research of simulation technologies of VSC-HVDC and DC grids

[J]. Power System Technology, 2018,42(1):1-12.

[本文引用: 1]

余晓鹏, 陆明, 张振安 , 等.

特高压直流对交流系统背景谐波的影响分析

[J]. 现代电力, 2014,31(4):39-43.

[本文引用: 1]

Yu Xiaopeng, Lu Ming, Zhang Zhenan , et al.

Analysis on harmonic influence of UHVDC on AC system

[J]. Modern Electric Power, 2014,31(4):39-43.

[本文引用: 1]

An T, Han C, Wu Y , et al.

HVDC grid test models for different application scenarios and load flow studies

[J]. Journal of Modern Power Systems and Clean Energy , 2017,5(2):262-274.

URL     [本文引用: 1]

周娟, 任国影, 魏琛 , 等.

电动汽车交流充电桩谐波分析及谐波抑制研究

[J]. 电力系统保护与控制, 2017,45(5):18-25.

[本文引用: 1]

Zhou Juan, Ren Guoying, Wei Chen , et al.

Harmonic analysis of electric vehicle AC charging spot and research on harmonic restriction

[J]. Power System Protection and Control, 2017,45(5):18-25.

[本文引用: 1]

张俨, 彭志炜, 雷章勇 , 等.

微电网谐波源危害及谐波检测技术

[J]. 电网与清洁能源, 2017,33(6):27-35,41.

[本文引用: 1]

Zhang Yan, Peng Zhiwei, Lei Zhangyong , et al.

Harmonic source hazard and harmonic detection technology in microgrid

[J]. Power System and Clean Energy, 2017,33(6):27-35,41.

[本文引用: 1]

Gursoy, Ekrem, Niebur, et al.

Harmonic load identification using complex independent component analysis

[J]. IEEE Transactions on Power Delivery, 2009,24(1):285-292.

URL     [本文引用: 1]

华回春, 贾秀芳, 张韶光 .

谐波责任定量评估的邻域多点测量方法

[J]. 电网技术, 2014,38(2):502-508.

[本文引用: 1]

Hua Huichun, Jia Xiufang, Zhang Shaoguang .

Neighborhood multi-point measurement method for harmonic contribution determination

[J]. Power System Technology, 2014,38(2):502-508.

[本文引用: 1]

华回春, 贾秀芳, 安海清 .

背景谐波波动情况下的谐波责任定量计算

[J]. 电测与仪表, 2014,51(7):1-8.

[本文引用: 1]

Hua Huichun, Jia Xiufang, An Haiqing .

Harmonic contributions determination under the background harmonic fluctuations

[J]. Electrical Measurement and Instrumentation, 2014,51(7):1-8.

[本文引用: 1]

Hua Huichun, Jia Xiufang, Cao Dongsheng , et al.

Practical method to determine the harmonic contribution of a specific harmonic load

[C]. 15th IEEE International Conference on Harmonics and Quality of Power,Hong Kong,China,June 17-20, 2012: 769-773.

[本文引用: 1]

张建军 .

谐波电压传递特性分析研究

[J]. 高压电器, 2016,52(10):130-134.

[本文引用: 2]

Zhang Jianjun .

Study of transfer characteristics of harmonic voltage

[J]. High Voltage Apparatus, 2016,52(10):130-134.

[本文引用: 2]

贾静然, 段晓波, 卢锦玲 , 等.

变压器的谐波传递特性研究

[J]. 中国电力, 2017,50(1):92-96,157.

[本文引用: 2]

Jia Jingran, Duan Xiaobo, Lu Jinling , et al.

Research on harmonic transfer characteristics of transformer

[J]. Electric Power, 2017,50(1):92-96,157.

[本文引用: 2]

曹雯佳 .

高压直流输电谐波传递特性的研究

[D]. 北京:华北电力大学, 2014.

[本文引用: 2]

/

〈 〉