1 引言
随着分布式电源广泛而分散接入电力系统中,系统越来越呈现出弱电网特征[1]。当系统内含有大量谐波源负荷时,配电网电压将会含有明显的背景谐波,进而导致并网逆变器的并网电流畸变。同时,弱电网条件下并网逆变器的稳定性会发生恶化。文献[2]从阻抗角度指出电网等效感抗增大会造成逆变器稳定裕度减小;文献[3]利用根轨迹分析了多台逆变器并联时,并联台数增加会导致闭环特征根出现在右半平面;文献[4]指出电网感抗变化会导致LCL型并网逆变器的谐振频率偏移从而削弱阻尼效果。为了减小电网电压扰动的影响,文献[5]从控制框图的等效变换角度推导出LCL型并网逆变器全前馈函数,以完全抵消畸变电网电压的扰动作用。然而弱电网条件下的电网电压前馈控制会引入额外的正反馈支路,从而降低系统对电网阻抗的鲁棒性[6],并提出实时测量电网阻抗和调整控制器参数的自适应控制方法。
针对上述方法的不足,本文首先建立数字控制下弱电网LCL型并网逆变器系统的控制模型,对比研究无电网电压前馈和直接比例前馈控制的特点。在此基础上提出一种具有宽范围选频特性的滞后选频前馈控制策略,以实现弱电网下系统稳态性能的改善。最后,在所搭建的单相LCL型并网逆变器实验平台上对本文所提策略的有效性进行了验证。
2 弱电网下LCL型并网逆变器的
数学建模
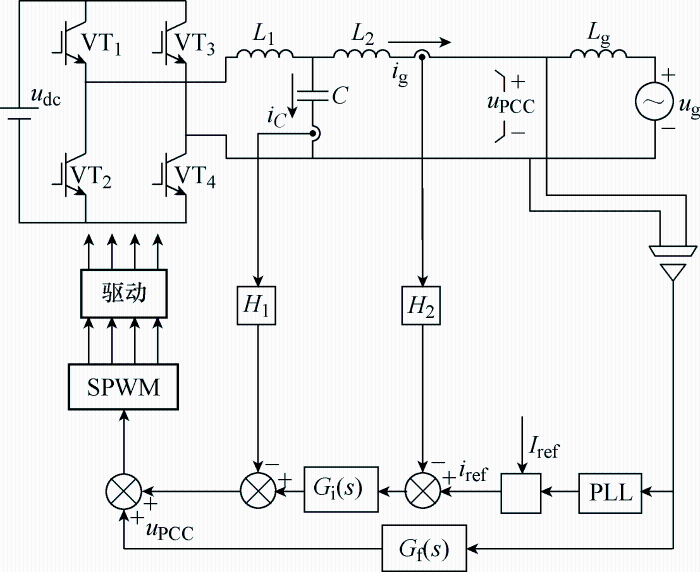
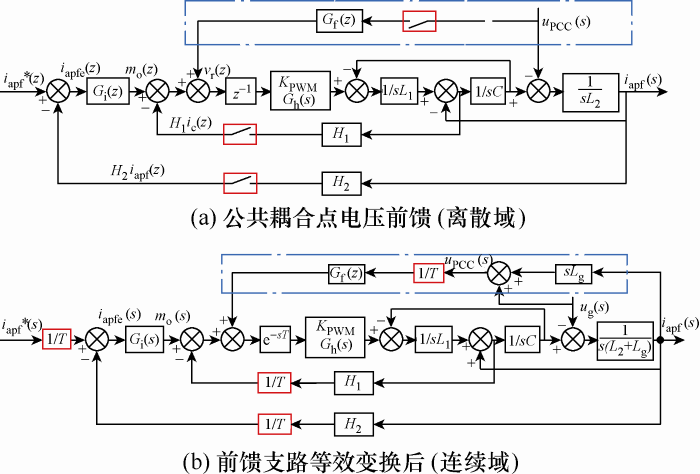
单相LCL型并网逆变器系统如图1所示,VT1、VT 2、VT 3、VT 4为氮化镓(GaN)开关管,其自身有反向续流能力,L1为逆变侧电感;L2为网侧电感;C为交流侧滤波电容;Lg为电网等效电感。图2为其控制系统传递函数框图,H2为网侧电流反馈系数;H1为电容电流反馈阻尼系数,采集电容电流的目的在于抑制LCL谐振尖峰。测量公共耦合点(PCC)电压用于锁相和电网电压前馈,Gf(s)为前馈函数;Gi(s)为电流调节器;采用比例谐振(PR)控制器。调制采用SPWM倍频方式,Gd(s)表征数字系统和PWM延迟,变换器的电压增益记为KPWM。设系统采样周期为T,则PWM调制过程的零阶保持作用近似为0.5T的延时环节,加之控制量更新固有延时1.0T,数字控制总延时为1.5T,故有:Gd(s)=exp(-1.5sT)。
图1
图2
电网电压前馈时,闭环系统的开环传递函数为
式中,${{G}_{\text{fg}}}\left( s \right)=s{{L}_{\text{g}}}{{G}_{\text{f}}}\left( s \right)$。
无电网电压前馈控制时,电流环开环传递函数为
式中,${{A}_{3}}={{L}_{1}}\left( {{L}_{2}}+{{L}_{\text{g}}} \right)C$;${{A}_{2}}=\left( {{L}_{2}}+{{L}_{\text{g}}} \right)C{{H}_{1}}{{K}_{\text{PWM}}}{{G}_{\text{d}}}\left( s \right)$;${{A}_{11}}={{L}_{1}}+{{L}_{2}}+{{L}_{\text{g}}}$。
当采用电网电压前馈时,电流环开环传递函数为
式中,${{A}_{12}}={{L}_{\text{g}}}{{G}_{\text{f}}}\left( s \right){{K}_{\text{PWM}}}{{G}_{\text{d}}}\left( s \right)$。
观察式(2)、(3)开环传递函数可知,无电网电压前馈时,电网感抗变化对系统稳定性影响可完全等效为LCL型并网逆变器网侧滤波参数的变化。而电网电压前馈后电流环开环传递函数分母一次项发生变化,电网感抗将直接影响到系统稳定性。尤其当电网较弱时,电网等效电感对并网逆变器的稳定性有显著影响。
电网电压扰动所引起的输出分量为
通过合理设计前馈函数可使得式(4)的分子为0,从而完全抵消电网电压对并网电流的扰动作用,此时可求得前馈函数满足
式(5)称为全前馈函数。
很明显,全前馈函数和控制延时、调制系数、输出滤波参数相关,这表明全前馈效果依赖输出滤波参数的准确性,且全前馈函数中一阶微分、二阶微分项容易引入微分噪声干扰问题[14]。
本文仅针对含有比例项的前馈方式展开分析,式(5)的全前馈函数可简化为
由于仅含有比例前馈项,故称式(6)为直接比例前馈控制。
3 弱电网下LCL型并网逆变器的
电网电压前馈改进策略
3.1 无前馈和直接比例前馈特点分析
表1 系统参数
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 额定容量/(kV·A) | 2.2 | 调制方式 | 倍频 |
| 额定电压/V | 220 | 逆变侧电感/mH | 0.99 |
| 额定电流/A | 10 | 滤波电容/μF | 1 |
| 开关频率/kHz | 50 | 网侧电感/mH | 0.44 |
| 采样频率/kHz | 50 | 谐振频率/kHz | 9.1 |
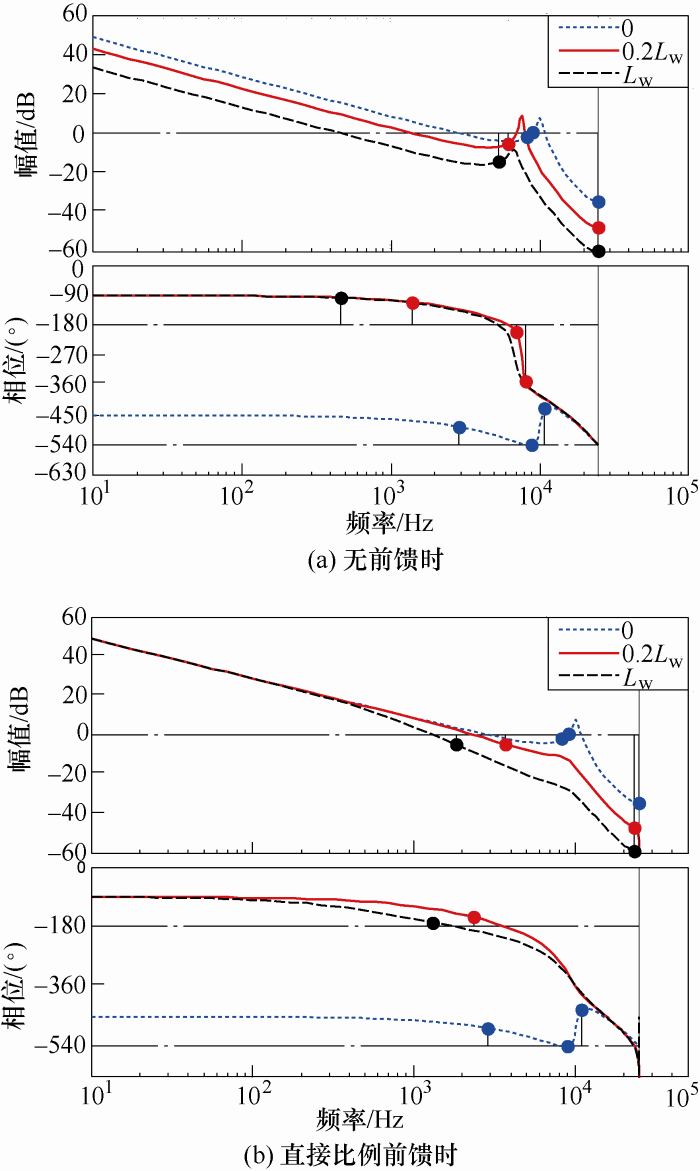
图3
上述两者差别之处,究其原因可以归结为以下两点:① 在谐振频率处系统的相位会突降180°,且直接比例前馈控制时,其等效谐振频率会严重受到电网电感的影响;② 直接比例前馈时近似实现了中低频段的幅频曲线和电网电感的解耦,从而在弱电网下系统开环截止频率仍然较高。正是这两点会造成直接比例前馈时系统的相位裕度随电网变弱而快速减小。因此,前馈通道必须衰减电网等效电感在中高频段前馈作用,才能保证弱电网下的稳定性。
3.2 弱电网下基于带通滤波前馈的电网电压前馈控制策略
式中,ωo 对应50 Hz的工频分量,Δω对应频率波动量,其取值一般考虑0.5 Hz的频率波动量。
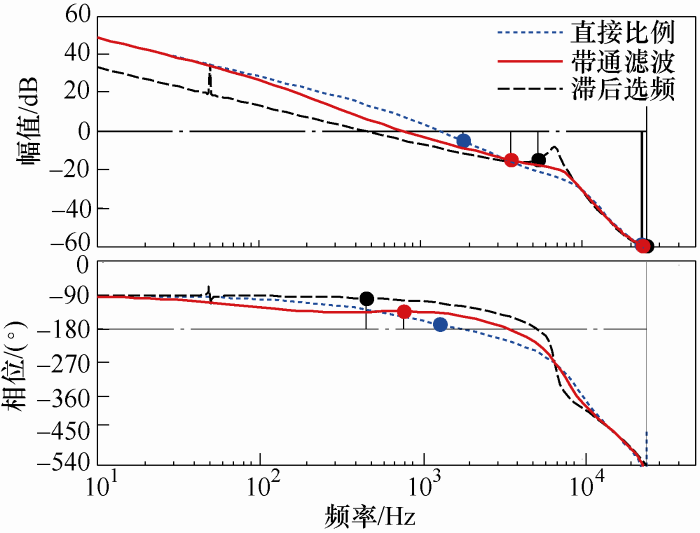
当Lg=0.2Lw时,带通滤波前馈下系统的开环伯德图如图4所示。该前馈方案的特点在于仅对工频分量进行有效前馈,此外和无前馈方案的伯德图完全相同,对其余分量等效于无前馈。因此带通滤波前馈可以获得良好的稳定性,但是对电网背景谐波电压无抑制作用,且动态特性差。
图4
3.3 弱电网下基于滞后选频前馈的改进电网电压前馈控制策略
综合考虑系统稳态、动态性能,可在前馈通道中引入具有低通特性的环节来改善系统稳定性,例如二阶低通滤波器。但是,二阶低通滤波器会在中高频段引入严重相移,不利于系统稳定性。经分析发现,式(8)滞后校正环节[17]具有所需要的低通高衰减特性。故本文选择滞后环节作为电网电压前馈通道上的选频校正环节。
式中,KPWM=1;b为小于1的常数;τ为时间常数。
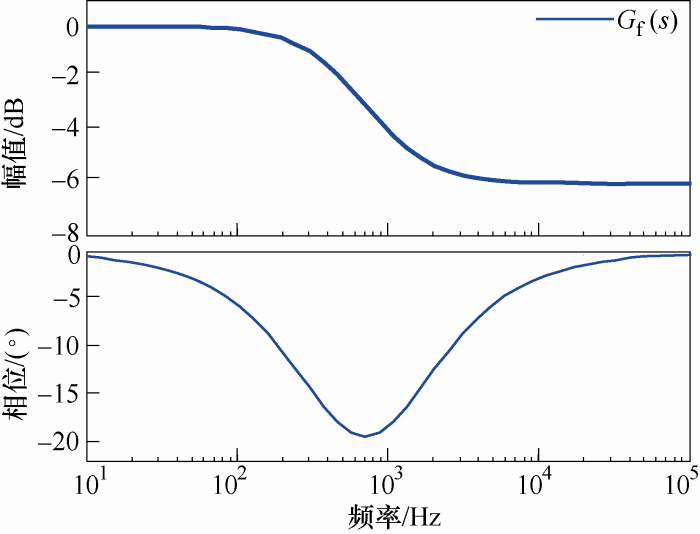
值得注意的是,滞后选频前馈函数在部分频段具有相位滞后特性,这是不利之处。因此,必须优化选择滞后选频环节的参数。首先,画出直接比例前馈系统下的开环伯德图,根据该伯德图设计滞后网络参数。同时,考虑到引入相位滞后大小、稳定性等约束条件,τ的选择应保证50 Hz信号不被衰减,1/2πτ明显大于工频50 Hz才能获得对电网电压背景谐波的高增益特性;b的选择必须保证前馈下的系统稳定性,且引入相移较小。选择的实际值如下:b=0.5,τ=1/(500×2π),此时式(8)所示滞后选频环节的频率特性如图5所示。
图5
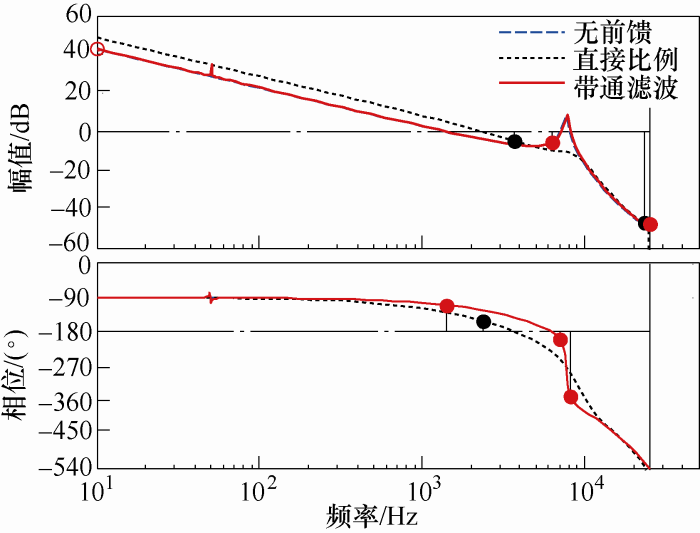
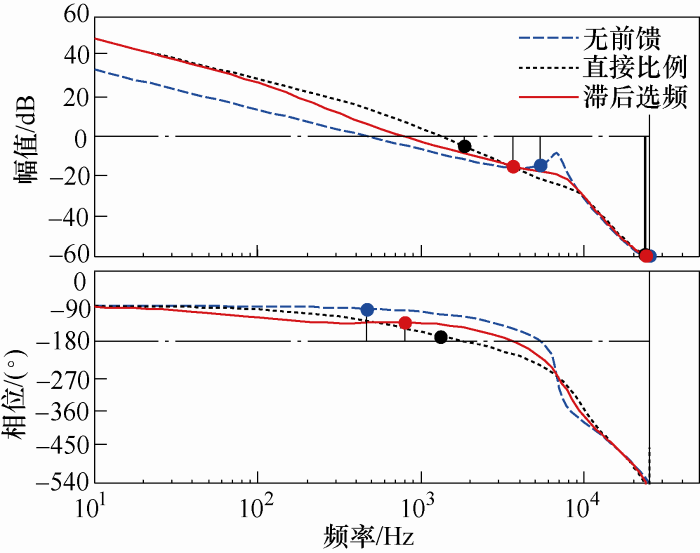
当Lg=0.2Lw时,无前馈、直接比例前馈、滞后选频前馈系统的开环伯德图如图6所示。显然,滞后选频前馈时幅值和相位穿越频率均介于其余两者之间,这是由于中高频率段前馈分量的衰减导致。故滞后选频前馈方案综合了无前馈和直接比例前馈的优点,系统的稳态、动态性能得到折衷。
图6
图7
4 试验分析
图8
图9
图10
图11
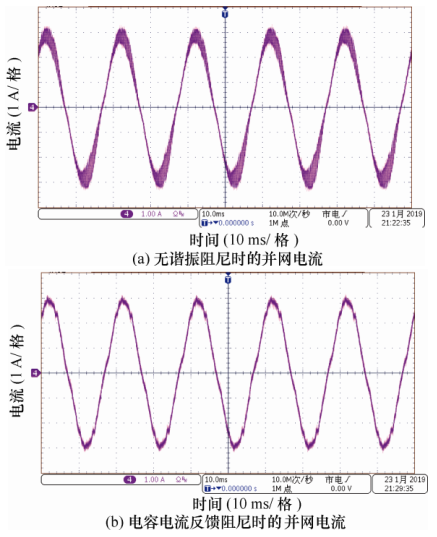
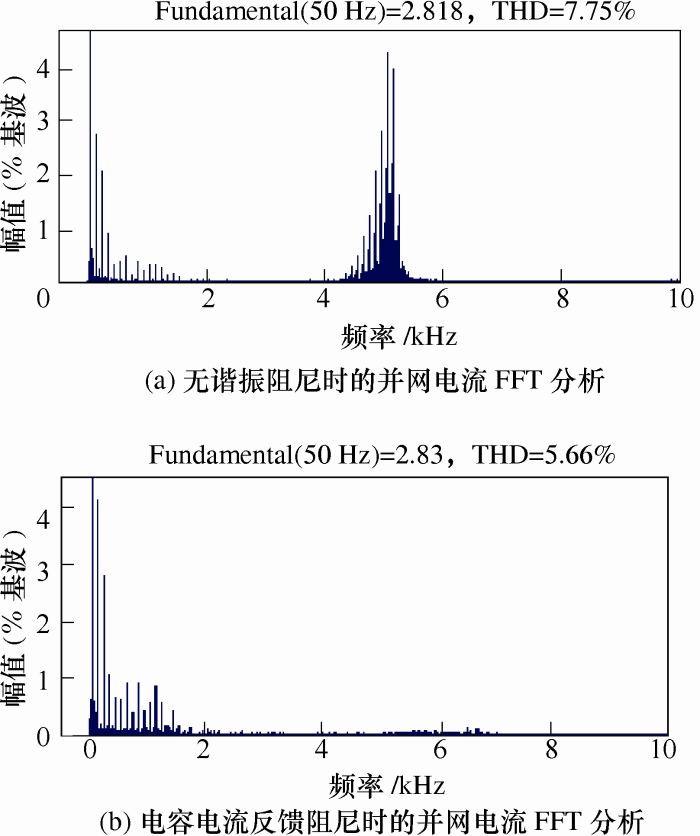
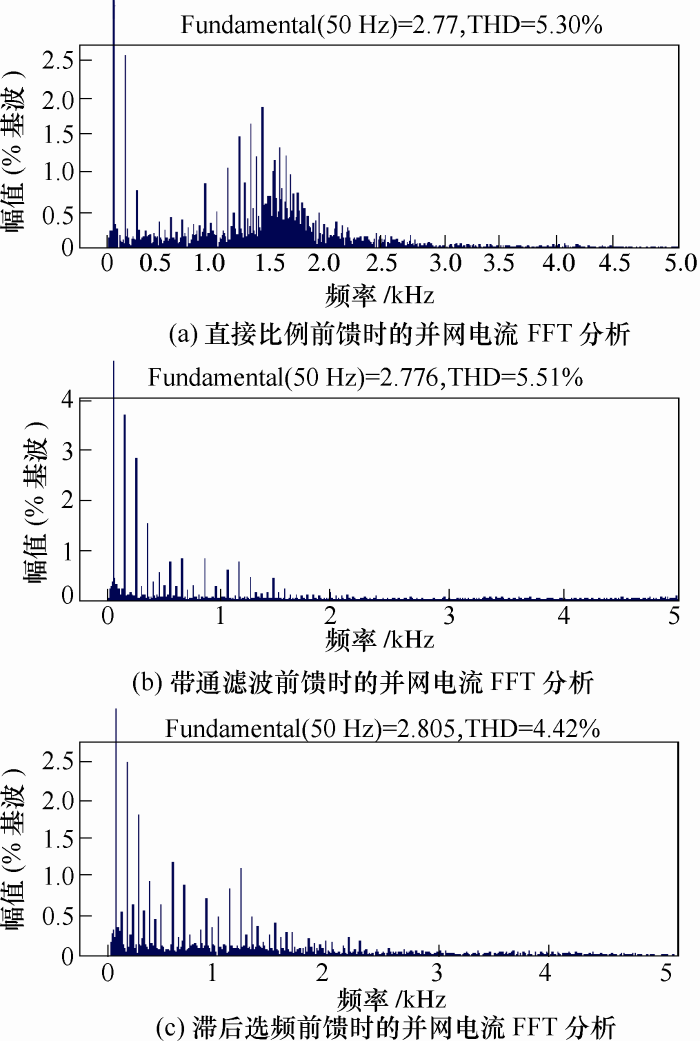
当采用带通滤波前馈和滞后选频前馈后,并网电流均稳定,THD依次为5.51%和4.42%。FFT分析表明,带通滤波前馈时并网电流的3次、5次、7次谐波含量分别为3.76%、2.89%、1.57%,而滞后选频前馈时并网电流的3次、5次、7次谐波含量分别为2.47%、1.82%、0.96%,故滞后选频前馈时并网电流质量更好。这是因为滞后选频环节设计在500 Hz以下时不衰减电网感抗的前馈作用,而后者只保留对50 Hz处的电网电压前馈作用。
5 结论
针对LCL型并网逆变器,本文重点研究了弱电网下电网电压前馈对并网逆变器稳定性的影响,并提出一种适用于弱电网下的滞后选频前馈策略,理论分析和试验结果表明以下几点。
(1) 采用滞后选频前馈策略的并网逆变器在稳定性方面对弱电网具有较强的适应性。
(2) 滞后选频前馈策略在提高对弱电网适应性的同时仍保持了较高的低频增益和穿越频率,系统响应快、网侧电流质量高。
参考文献
Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values
[J].
感性电网阻抗下三相光伏逆变器稳定性分析
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.18.006
URL
Magsci
[本文引用: 1]

许多情况下,电网并非理想的电压源,而是存在感性阻抗的弱电网。传统的光伏逆变器设计并没有考虑电网阻抗的影响,逆变器-电网级联系统阻抗不匹配容易导致逆变器的稳定性能降低,甚至不稳定。该文从阻抗的角度,分析L滤波和LCL滤波的光伏逆变器在感性电网阻抗下的稳定性,并分别对稳定判据和输出导纳模型展开研究。通过模型降阶和矩阵近似,简化广义奈奎斯特稳定判据对逆变器-电网级联系统的稳定性分析。借鉴直流电源导纳模型建立的方法,简化由闭环状态矩阵推导<i>d</i>轴输出导纳的计算过程。最后根据所提出的简化判据和建立的<i>d</i>轴输出导纳模型,分析两种滤波方式下级联系统的稳定性,并研究滤波器参数与对级联系统稳定裕度的影响。通过实验对所进行的稳定性分析进行了验证。
Stability analysis of three-phase photovoltaic inverter under inductive grid impedance
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.18.006
URL
Magsci
[本文引用: 1]

许多情况下,电网并非理想的电压源,而是存在感性阻抗的弱电网。传统的光伏逆变器设计并没有考虑电网阻抗的影响,逆变器-电网级联系统阻抗不匹配容易导致逆变器的稳定性能降低,甚至不稳定。该文从阻抗的角度,分析L滤波和LCL滤波的光伏逆变器在感性电网阻抗下的稳定性,并分别对稳定判据和输出导纳模型展开研究。通过模型降阶和矩阵近似,简化广义奈奎斯特稳定判据对逆变器-电网级联系统的稳定性分析。借鉴直流电源导纳模型建立的方法,简化由闭环状态矩阵推导<i>d</i>轴输出导纳的计算过程。最后根据所提出的简化判据和建立的<i>d</i>轴输出导纳模型,分析两种滤波方式下级联系统的稳定性,并研究滤波器参数与对级联系统稳定裕度的影响。通过实验对所进行的稳定性分析进行了验证。
电网阻抗对大型并网光伏系统稳定性影响分析
[J].当电网阻抗较高时,并网光伏系统会变得不稳定;特别是连接在弱电网上的大型光伏电站,稳定性问题更为突出。为研究电网阻抗对大型并网光伏系统稳定性影响,该文建立了三相逆变器并联系统的诺顿等效模型,推导了逆变器并网电流、并网公共点电压表达式以及大型并网光伏系统的闭环特征方程,采用根轨迹法分析了电网阻抗对大型并网光伏系统稳定性的影响,最后建立系统仿真模型进行验证,结果表明,三相逆变器的诺顿等效模型相间不存在耦合效应,三相逆变器并联系统的特性分析可在单相逆变器并联系统。
Analysis of the influence of grid impedance on the stability of large-scale grid-connected photovoltaic system
[J].当电网阻抗较高时,并网光伏系统会变得不稳定;特别是连接在弱电网上的大型光伏电站,稳定性问题更为突出。为研究电网阻抗对大型并网光伏系统稳定性影响,该文建立了三相逆变器并联系统的诺顿等效模型,推导了逆变器并网电流、并网公共点电压表达式以及大型并网光伏系统的闭环特征方程,采用根轨迹法分析了电网阻抗对大型并网光伏系统稳定性的影响,最后建立系统仿真模型进行验证,结果表明,三相逆变器的诺顿等效模型相间不存在耦合效应,三相逆变器并联系统的特性分析可在单相逆变器并联系统。
增强LCL型并网逆变器对电网阻抗鲁棒性的控制参数设计
[J].
DOI:10.13334/j.0258-8013.pcsee.2015.10.023
URL
Magsci
[本文引用: 1]

电容电流反馈有源阻尼是抑制并网逆变器中LCL滤波器谐振的有效方式。然而,由于实际电网存在变化的电网阻抗,LCL滤波器的谐振频率会在宽范围内变化,使得电容电流反馈系数的选取变得困难。特别地,当谐振频率等于1/6的采样频率(<em>f</em><sub>s</sub>/6)时,无论选取多大的电容电流反馈系数,系统都无法稳定。研究适应电网阻抗宽范围变化的电容电流反馈系数的设计方法,针对不同的谐振频率,推导出系统稳定时的幅值裕度要求,通过分析电网阻抗对幅值裕度的影响,得到最优的电容电流反馈系数。采用这个反馈系数时,除了谐振频率等于<em>f</em><sub>s</sub>/6之外,系统都能保持稳定。进一步地,为了提高谐振频率等于<em>f</em><sub>s</sub>/6时系统的稳定性,提出环路增益的相位滞后补偿方法。最后,在一台6 kW的原理样机进行实验验证,实验结果证明了理论分析的正确性。
Control parameter design of enhanced LCL grid-connected inverter for grid impedance robustness
[J].
DOI:10.13334/j.0258-8013.pcsee.2015.10.023
URL
Magsci
[本文引用: 1]

电容电流反馈有源阻尼是抑制并网逆变器中LCL滤波器谐振的有效方式。然而,由于实际电网存在变化的电网阻抗,LCL滤波器的谐振频率会在宽范围内变化,使得电容电流反馈系数的选取变得困难。特别地,当谐振频率等于1/6的采样频率(<em>f</em><sub>s</sub>/6)时,无论选取多大的电容电流反馈系数,系统都无法稳定。研究适应电网阻抗宽范围变化的电容电流反馈系数的设计方法,针对不同的谐振频率,推导出系统稳定时的幅值裕度要求,通过分析电网阻抗对幅值裕度的影响,得到最优的电容电流反馈系数。采用这个反馈系数时,除了谐振频率等于<em>f</em><sub>s</sub>/6之外,系统都能保持稳定。进一步地,为了提高谐振频率等于<em>f</em><sub>s</sub>/6时系统的稳定性,提出环路增益的相位滞后补偿方法。最后,在一台6 kW的原理样机进行实验验证,实验结果证明了理论分析的正确性。
Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics
[J].
弱电网下LCL滤波并网逆变器自适应电流控制
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.24.006
URL
Magsci
[本文引用: 1]

由电网电压谐波以及电网阻抗变化等引起的电网不确定性严重影响LCL型并网逆变器的电流控制。电网电压比例前馈因实现方便且可有效地抑制电网谐波的作用而获得了广泛的关注,但少有文献探讨其在电网阻抗大幅变化即弱电网下的性能。该文分析表明,弱电网下该前馈补偿会大幅降低电流控制的稳定裕度。随着电网阻抗中感性成分的增大稳定裕度变差,最终导致不稳定。此外,低次谐波电流抑制也会失效。针对上述问题,提出一种基于电网阻抗估测的自适应控制方法,即时修正用于前馈补偿的电压以及调整调节器参数以保证较好的相位裕度或高带宽。对比分析以及实验研究表明提出的方案可有效地提高LCL滤波并网逆变器的电网适应性。
Adaptive current control of LCL filtered grid-connected inverter under weak power grid
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.24.006
URL
Magsci
[本文引用: 1]

由电网电压谐波以及电网阻抗变化等引起的电网不确定性严重影响LCL型并网逆变器的电流控制。电网电压比例前馈因实现方便且可有效地抑制电网谐波的作用而获得了广泛的关注,但少有文献探讨其在电网阻抗大幅变化即弱电网下的性能。该文分析表明,弱电网下该前馈补偿会大幅降低电流控制的稳定裕度。随着电网阻抗中感性成分的增大稳定裕度变差,最终导致不稳定。此外,低次谐波电流抑制也会失效。针对上述问题,提出一种基于电网阻抗估测的自适应控制方法,即时修正用于前馈补偿的电压以及调整调节器参数以保证较好的相位裕度或高带宽。对比分析以及实验研究表明提出的方案可有效地提高LCL滤波并网逆变器的电网适应性。
提高LCL型并网逆变器对电网阻抗鲁棒性的阻抗调节方法
[J].
Impedance adjustment method for improving the robustness of LCL grid-connected inverters to grid impedance
[J].
提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.15.001
URL
Magsci
[本文引用: 1]

随着分布式电源并网功率等级的增加及接入位置的广泛分布, 电网越来越表现出弱电网的特性, 即含有较大的电网阻抗和丰富的电网电压背景谐波。其中, 电网阻抗会改变控制环路的增益, 影响其控制性能, 甚至可能导致系统不稳定, 而电网电压背景谐波会引起并网电流的畸变, 使其无法满足并网电流谐波标准。由于逆变器的输出阻抗模型能够同时反映控制系统对电网阻抗的鲁棒性及对电网电压的抗扰性能, 因此, 该文通过揭示它们之间的关系, 提出采用虚拟阻抗的方法对输出阻抗进行校正, 并给出虚拟阻抗的实现过程和参数的设计方法。采用该方法可使得逆变器在电网阻抗宽范围变化时仍然能够稳定工作, 同时保证并网电流满足谐波标准。以单相LCL型并网逆变器为例进行实验验证, 实验结果验证了控制策略的有效性。
Virtual impedance method for improving the adaptability of LCL grid-connected inverter to weak grid
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.15.001
URL
Magsci
[本文引用: 1]

随着分布式电源并网功率等级的增加及接入位置的广泛分布, 电网越来越表现出弱电网的特性, 即含有较大的电网阻抗和丰富的电网电压背景谐波。其中, 电网阻抗会改变控制环路的增益, 影响其控制性能, 甚至可能导致系统不稳定, 而电网电压背景谐波会引起并网电流的畸变, 使其无法满足并网电流谐波标准。由于逆变器的输出阻抗模型能够同时反映控制系统对电网阻抗的鲁棒性及对电网电压的抗扰性能, 因此, 该文通过揭示它们之间的关系, 提出采用虚拟阻抗的方法对输出阻抗进行校正, 并给出虚拟阻抗的实现过程和参数的设计方法。采用该方法可使得逆变器在电网阻抗宽范围变化时仍然能够稳定工作, 同时保证并网电流满足谐波标准。以单相LCL型并网逆变器为例进行实验验证, 实验结果验证了控制策略的有效性。
弱电网下并网逆变器自适应H∞控制方法
[J].
Adaptive H∞ control method for grid-connected inverters in weak grids
[J].
一种提升逆变器对电网适应能力的电流控制策略
[J].
A current control strategy for improving the adaptability of inverters to power grids
[J].
弱电网条件下LCL型并网逆变器谐振前馈控制策略研究
[J].
Research on resonant feedforward control strategy of LCL grid-connected inverter under weak grid conditions
[J].
增强并网逆变器对电网阻抗鲁棒稳定性的改进前馈控制方法
[J].
Improved feedforward control method for enhanced robust stability of grid-connected inverters to grid impedance
[J].
Regions of active damping control for LCL filters
[J].
DOI:10.1109/TIA.2013.2266892
URL
Magsci
[本文引用: 1]

The control of a grid-connected voltage source inverter with an inductive-capacitive-inductive (LCL) filter is a very challenging task, since the LCL network causes a resonance phenomenon near to the control stability boundary. While many active damping methods have been proposed to overcome this issue, the role that pulse width modulation transport delay plays in the effectiveness of these strategies is still not fully resolved. This paper presents a theoretical discrete time-analysis framework that identifies three distinct regions of LCL filter resonance, namely, a high resonant frequency region where active damping is not required, a critical resonant frequency where a controller cannot stabilize the system, and a low resonant frequency region where active damping is essential. Suitable controllers are then proposed for the two stable regions, with gain calculations that allow for the greatest system bandwidth and damping. Simulation and experimental results verify the presented analysis.