电气工程学报, 2019, 14(2): 7-11 doi: 10.11985/2019.02.002

基于基波阻抗辨识的短路比测量方法 *

陈巧地, 张兴, 李明, 刘晓玺, 郭梓暄

合肥工业大学电气与自动化工程学院 合肥 230009

Short Circuit Ratio Measurement Method Based on Fundamental Impedance Detection

CHEN Qiaodi, ZHANG Xing, LI Ming, LIU Xiaoxi, GUO Zixuan

School of Electrical Engineering and Automation, Hefei University of Technology, Hefei 230009 China

收稿日期: 2019-05-5   网络出版日期: 2019-06-25

基金资助: * 国家重点研发计划资助项目.  2016YFB0900300

Received: 2019-05-5   Online: 2019-06-25

作者简介 About authors

陈巧地,男,1994年生,硕士研究生。主要研究方向为弱电网下并网逆变器的稳定性。E-mail：1845183643@qq.com;

张兴,男,1963年生,博士,教授。主要研究方向为新能源发电。E-mail：hongLf@ustc.edu.cn

摘要

随着新能源、无功补偿等电力电子设备的大量接入,交流电网系统不断变弱,分析交流并网系统的稳定性、精确度量交流并网系统的强度十分重要。短路比(SCR)作为衡量并网系统强度的一个重要因素,提出了一种基于基波阻抗辨识的短路比测量方法。首先,针对传统阻抗辨识实时性差、精度低的问题,提出了一种基于递归离散傅里叶变换的谐波提取方法,进而计算基波阻抗。其次,以两台逆变器并网系统为例,提出短路比测量方案。最后通过仿真和试验验证了测量方法的合理性和有效性。

关键词： 基波阻抗 ; 递归离散傅里叶变换 ; 并网系统强度 ; 短路比

Abstract

：More and more renewable energy generators and reactive power compensation devices are connected to AC power systems, which make AC grid systems weaker and weaker, so it is important to measure the strength of AC grid systems and analyze stability of the systems. Short circuit ratio (SCR) plays an important role in measuring the strength of systems. A method of short circuit ratio measurement based on fundamental impedance detection is established. Firstly, aiming at the problem of poor real-time performance and low accuracy of traditional impedance identification, a recursive discrete Fourier transform based harmonic extraction method is proposed to calculate fundamental impedance. Secondly, taking the grid-connected system of two inverters as an example, a short-circuit ratio measurement scheme is proposed. Finally, the rationality and validity of the measurement method are verified by simulation and experiment.

Keywords： Fundamental impedance ; recursive discrete Fourier transform ; grid-connected system strength ; short circuit ratio

PDF (549KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈巧地, 张兴, 李明, 刘晓玺, 郭梓暄. 基于基波阻抗辨识的短路比测量方法 *. 电气工程学报[J], 2019, 14(2): 7-11 doi:10.11985/2019.02.002

CHEN Qiaodi. Short Circuit Ratio Measurement Method Based on Fundamental Impedance Detection. Journal of Electrical Engineering[J], 2019, 14(2): 7-11 doi:10.11985/2019.02.002

1 引言

随着化石能源的不断消耗以及环境危机的日益加剧,光伏、风电等新能源在电力结构中的比重越来越大,多并网逆变器接入同一交流电网不可避免,这些距离较近的新能源和交流电网一起构成多逆变器并网系统[1,2]。

当多逆变器并网系统的并网逆变器数量不断增加且容量增大后,交流电网的支撑能力就会减弱,导致设备与设备、设备与电网之间的耦合作用加剧,进而可能引起系统出现谐振现象。因此,如何测量和评估多逆变器接入后电网的强度,定量分析多逆变器并网系统之间的相互作用,对保证系统的稳定运行十分重要[3,4,5]。

短路比(Short circuit ratio,SCR)常被用于分析多逆变器并网系统的相对强度和稳定性：SCR越大,交流电网越强,多逆变器并网系统越稳定,反之系统越不稳定[6]。文献[7]由单馈入系统出发,提出了电力电子多馈入系统短路比的定义,并给出了系统的稳定边界。但逆变器本身如何测量自己所处系统的强弱情况,没有给出方案。文献[8]通过测量宽频带的电网阻抗,利用阻抗稳定性判据衡量并网系统的强弱。但这种方法需要测量大量频率点处的阻抗值,实时性较差,很难实现并网逆变器的在线检测。

针对上述问题,本文提出了一种基于基波阻抗辨识的短路比测量方法。通过将多逆变器并网系统等效成两逆变器并网系统,针对两逆变器系统,通过测量基波阻抗,利用基波阻抗和并网系统短路比之间的关系,在线测量得到系统的短路比。

首先,针对传统阻抗检测实时性差、精度低的缺点,提出了基于递归离散傅里叶变换的谐波提取方法,进而计算基波阻抗。其次,以两台逆变器并网系统为例,提出短路比测量方案。最后通过仿真和试验验证了测量方法的合理性和有效性。

2 电网基波阻抗辨识原理

2.1 三相并网系统拓扑结构

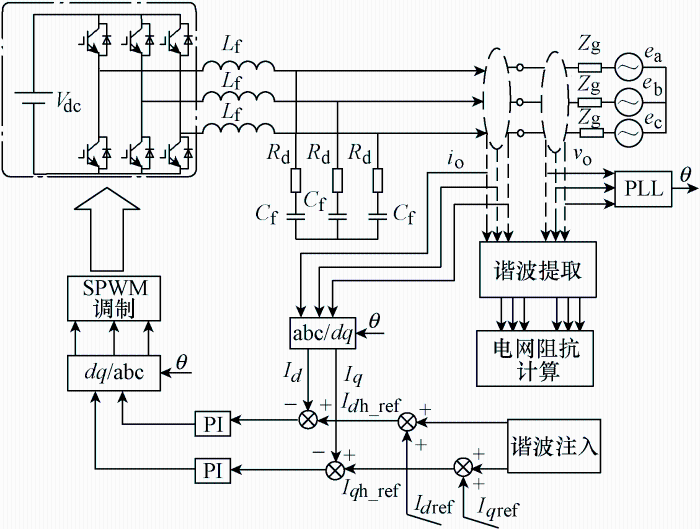
图1为典型的三相并网系统拓扑结构及控制结构。其中, V_{dc}为直流电压; L_{f}和C_{f}构成LC滤波器;R_{d}为阻尼电阻;Z_{g}为电网阻抗;v_{o}为公共耦合点(Point of common coupling, PCC)电压;i_{o}为公共耦合点并网电流。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   三相并网逆变器系统拓扑及控制结构


2.2 基波阻抗辨识原理

图1并网系统中,在给定电流上叠加频率为${{f}_{\text{h}}}$的扰动电流,经过控制环节会在PCC点产生电压和电流响应,采用傅里叶变换提取${{f}_{\text{h}}}$频率下的电压分量和电流分量,进而通过计算得到基波阻抗。

由于电网中含有丰富的背景谐波,在扰动信号频率的选择上,一方面为了尽可能地避开背景谐波的影响,通常选择非特征次谐波注入;另一方面为了能够尽可能地减弱频率变换带来的误差,通常选择距离基波频率较近的谐波,综合考虑本文选择谐波电流扰动的频率为75 Hz。

如图1所示,在并网逆变器控制中,通过在电流参考值上叠加扰动信号,经控制环节在PCC处产生电压响应${{v}_{\text{o}}}\left( t \right)$和电流响应${{i}_{\text{o}}}\left( t \right)$,经离散傅里叶变换提取响应信号中的谐波分量${{v}_{\text{th}}}$和${{i}_{\text{th}}}$,即

$\left\{ \begin{align} & {{v}_{\text{th}}}=F\left( {{v}_{\text{o}}}\left( t \right) \right) \\ & {{i}_{\text{th}}}=F\left( {{i}_{\text{o}}}\left( t \right) \right) \\ \end{align} \right.$

利用式(1)计算得到并网点阻抗Zm为

${{Z}_{\text{m}}}=\frac{{{v}_{\text{th}}}-{{v}_{\text{th0}}}}{{{i}_{\text{th}}}-{{i}_{\text{th0}}}}$

其中,${{v}_{\text{th0}}}$和${{i}_{\text{th0}}}$为未注入扰动时的谐波信号。

从上述分析可以看出,阻抗辨识的核心是非特征次谐波的提取。传统的谐波提取方法有快速傅里叶变换(Fast Fourier transformation, FFT)和离散傅里叶变换(Discrete Fourier transform, DFT),但上述两种方法在计算方面都需要占用大量的内存空间和计算时间。近些年来,有学者提出一种递归离散傅里叶算法(Recursive discrete Fourier transform, RDFT),通过观察DFT和FFT算法可以发现,连续两个采样时刻的样本只是将前一时刻样本的第一个采样值舍弃,在最后加上最新的采样值获得,RDFT算法正是基于上述认识推导而来。

对任意周期信号$x(t)$,若其周期为$T$,设置采样点数为$N$,则其任意时刻的值可以用各次频率分量之和表示为

$x\left( kT \right)=\sum\limits_{n=1}^{{{N}_{\text{m}}}}{{{A}_{n}}\cos nwkT+}\sum\limits_{n=1}^{{{N}_{\text{m}}}}{{{B}_{n}}\sin nwkT}$

式中

$\left\{ \begin{align} & {{A}_{n}}=\frac{2}{N}\sum\limits_{i=1}^{N-1}{x(i\tau )\cos n\omega i\tau } \\ & {{B}_{n}}=\frac{2}{N}\sum\limits_{i=1}^{N-1}{x(i\tau )\sin n\omega i\tau } \\ \end{align} \right.$

式中,${{A}_{n}}$、${{B}_{n}}$分别为n次频率分量的正弦、余弦分量的幅值;$k=0$,1,2,3,$\cdots $,$N-1$;采样间隔$\tau =T/N$。

以计算基波为例,对式(4)进行改造可得

$\left\{ \begin{align} & {{A}_{1}}=\frac{2}{N}\sum\limits_{i=N\text{c}}^{{{N}_{\text{c}}}-N+1}{x(i\tau )cos\omega i\tau } \\ & {{B}_{1}}=\frac{2}{N}\sum\limits_{i={{N}_{\text{c}}}}^{{{N}_{\text{c}}}-N+1}{x(i\tau )sin\omega i\tau } \\ \end{align} \right.$

其中,${{N}_{\text{c}}}$为新的采样点。

观察式(5)可以发现,当前采样时刻计算A1、B1与上一时刻${{{A}'}_{1}}$、${{{B}'}_{1}}$的计算值存在如下迭代关系

$\left\{ \begin{align} & {{A}_{1}}={{{{A}'}}_{1}}+\frac{2}{N}\left[ x({{N}_{\text{c}}}\tau )-x(({{N}_{\text{c}}}-N)\tau ) \right]\cos \omega {{N}_{\text{c}}}\tau \\ & {{B}_{1}}={{{{B}'}}_{1}}+\frac{2}{N}\left[ x({{N}_{\text{c}}}\tau )-x(({{N}_{\text{c}}}-N)\tau ) \right]\sin \omega {{N}_{c}}\tau \\ \end{align} \right.$

由式(6)可知,在已知前一时刻计算值的基础上,只要通过简单的减法和乘法就可以得到新的值。整个递归计算过程只需要在初始化阶段的一个工频周期内完成周期求和运算,之后就可以按照式(6)递归计算来完成,从而大大减小了计算量。

用DFT和RDFT对同一谐波采样信号进行检测分析,采样点数设为N,提取谐波总数设为N,这两种算法的计算量和响应速度对比见下表。

表   采用RDFT和DFT算法比较

算法类型RDFTDFT
复乘次数NN ²
复加次数2NN(N-1)
响应速度快慢
单次谐波检测能能

新窗口打开| 下载CSV


由上表可知,RDFT在减小运算量方面相比DFT具有较大优势。实际计算过程中,采样频率越高,对应采样点数N越大,RDFT在减小运算量方面优势更加突出。

3 并网系统短路比测量原理

3.1 短路比定义

在多逆变器控制系统中,常用短路比来衡量交流系统的强度。短路比定义为交流电网的短路容量与电力电子设备的接入容量之比,即

$SCR=\frac{{{S}_{\text{ac}}}}{{{S}_{\text{B}}}}$

式中,${{S}_{\text{ac}}}$为交流电网短路容量;${{S}_{\text{B}}}$为电力电子设备的接入容量。

上级调度部门可以获知每台并网逆变器的接入容量,并且交流电网的短路容量已知,所以很容易得知系统的短路比。但对于单台逆变器,在没有通信的前提下很难直接获得所处并网系统的短路容量,本文提出了一种基于基波阻抗辨识的短路比测量方法。

3.2 基于基波阻抗辨识的短路比测量原理

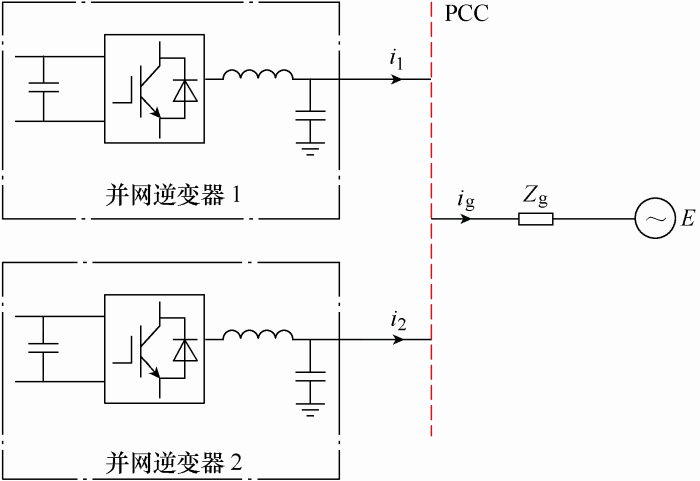
考虑到多逆变器可以等效成两逆变器系统[9],所以本文以两逆变器系统为例,研究基于基波阻抗辨识的短路比测量原理。

图2为两逆变器并网系统,对于并网逆变器1而言,其自身投入电网的容量已知,记为S1,电网阻抗为${{Z}_{\text{g}}}$,电网的短路容量为${{S}_{\text{ac}}}$。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   两并网逆变器系统结构图


当并网逆变器1正常开机工作时,利用上述所提的阻抗辨识方法,测量此时的基波阻抗为Z1,当并网逆变器2接入后,测得的电网阻抗为Z2,可以得到该并网系统下电力电子设备的投入容量为

${{S}_{\text{B}}}={{S}_{1}}+{{S}_{2}}={{S}_{1}}+k\left( {{Z}_{2}}-{{Z}_{1}} \right)$

式中,${{S}_{\text{B}}}$为电力电子设备的投入容量;${{S}_{2}}$为并网逆变器2的投入容量;$k$为注入扰动与逆变器容量之间的比例关系,工程中一般取5%~10%。

由式(7)、(8)可以计算得到短路比,计算方法为

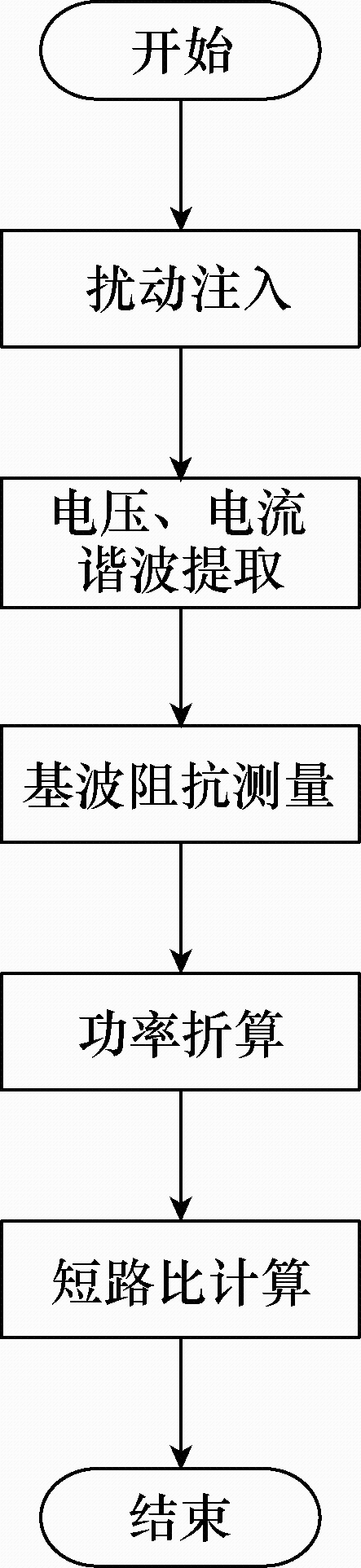
$SCR=\frac{{{S}_{\text{ac}}}}{{{S}_{B}}}=\frac{{{S}_{\text{ac}}}}{{{S}_{\text{B}}}}=\frac{{{S}_{\text{ac}}}}{{{S}_{\text{1}}}+k\left( {{Z}_{2}}-{{Z}_{1}} \right)}$

具体流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   短路比测量流程图


4 仿真和试验

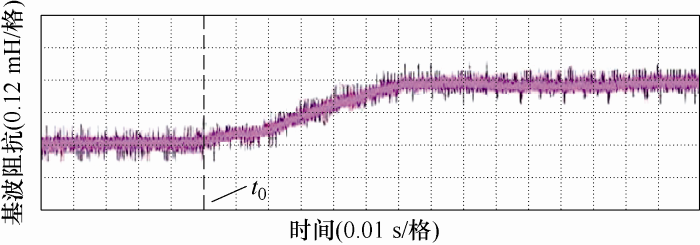
4.1 仿真验证

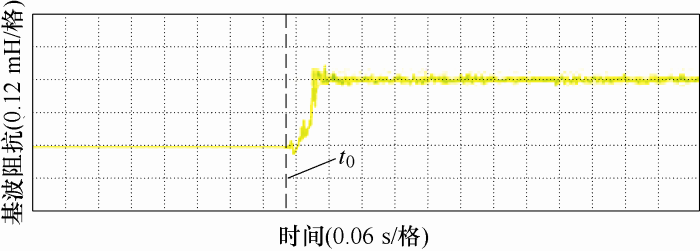
为了验证上述理论分析的正确性,利用Matlab/ Simulink搭建了两台三相并网逆变器的仿真平台。电网阻抗${{Z}_{2}}$仅考虑电感成分为0.24 mH。首先一台100 kW并网逆变器(记为1#)投入并网运行,在t0时刻投入第二台100 kW并网逆变器(记为2#),在2#并网逆变器投入前后基波阻抗的测量值如图4所示,测得的短路比如图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   基波阻抗测量仿真波形


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   短路比测量仿真波形


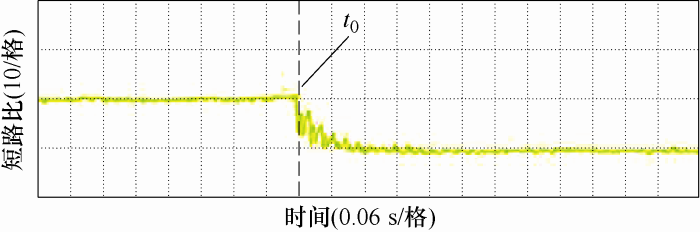
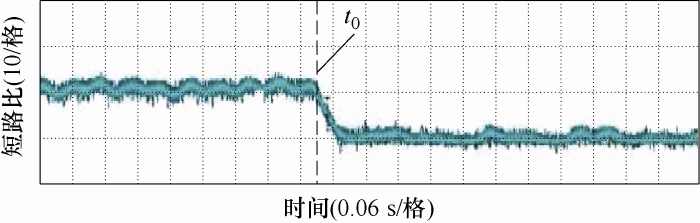
可以发现,在投入2#并网逆变器后基波阻抗增加为原来的2倍,短路比减小为原来的一半。

4.2 试验验证

为了验证本文所提方法的正确性,搭建了如图6所示的试验平台,图6中1#、2#并网逆变器容量为100 kW;直流源由两台100 kW整流器提供。采用DSP TMS28377D型并网逆变器及整流器进行控制。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   试验平台


试验工况和仿真工况完全一致。图7给出了投入2#并网逆变器前后测得的基波阻抗变化情况,图8给出了投入2#并网逆变器前后测得的短路比变化情况,试验波形和仿真波形吻合。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   基波阻抗测量试验波形


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   短路比测量试验波形


5 结论

本文提出了一种基于基波阻抗辨识的短路比测量方法,并结合Matlab/Simulink仿真和试验,验证了该方法的正确性。结论如下所述。

(1) 采用谐波扰动方案可以精确地检测基波阻抗。

(2) 本文从基波阻抗出发,得出了基波阻抗与并网系统短路比的关系,并提出了一种短路比测量方法,为后续的稳定性判定及自适应控制提供了便利。

参考文献

Liu Hong, Zeng Pingliang, Guo Jianyi , et al.

An optimization strategy of controlled electric vehicle charging considering demand side response and regional wind and photovoltaic

[J]. Journal of Modern Power Systems and Clean Energy, 2015,3(2):232-239.

URL     [本文引用: 1]

孙荣富, 张涛, 梁吉 .

电网接纳风电能力的评估及应用

[J]. 电力系统自动化, 2011,35(4):70-76.

[本文引用: 1]

Sun Rongfu, Zhang Tao, Liang Ji .

Evaluation and application of wind power integration capacity in power grid

[J]. Automation of Electric Power Systems, 2011,35(4):70-76.

[本文引用: 1]

胡伟, 孙建军, 马谦 , 等.

多个并网逆变器间的交互影响分析

[J]. 电网技术, 2014,38(9):2511-2518.

[本文引用: 1]

Hu Wei, Sun Jianjun, Ma Qian , et al.

Analysis on interactive influences among multi grid-connected inverters

[J]. Power System Technology, 2014,38(9):2511-2518.

[本文引用: 1]

Sun Jian .

Impedance based stability criterion for grid connected inverters

[J]. IEEE Transactions on Power Electronics, 2011,26(11):3075-3078.

DOI:10.1109/TPEL.2011.2136439      URL     Magsci     [本文引用: 1]

Grid-connected inverters are known to become unstable when the grid impedance is high. Existing approaches to analyzing such instability are based on inverter control models that account for the grid impedance and the coupling with other grid-connected inverters. A new method to determine inverter-grid system stability using only the inverter output impedance and the grid impedance is developed in this paper. It will be shown that a grid-connected inverter will remain stable if the ratio between the grid impedance and the inverter output impedance satisfies the Nyquist stability criterion. This new impedance-based stability criterion is a generalization to the existing stability criterion for voltage-source systems, and can be applied to all current-source systems. A single-phase solar inverter is studied to demonstrate the application of the proposed method.

谢少军, 季林, 许津铭 .

并网逆变器电网阻抗检测技术综述

[J]. 电网技术, 2015,39(2):320-326.

[本文引用: 1]

Xie Shaojun, Ji Lin, Xu Jinming .

Review of grid impedance estimation for gird-connected inverter

[J]. Power System Technology, 2015,39(2):320-326.

[本文引用: 1]

Zhou J Z, Ding Hui, Fan Shengtao , et al.

Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter

[J]. IEEE Transactions on Power Delivery, 2014,29(5):2287-2296.

DOI:10.1109/TPWRD.2014.2330518      URL     Magsci     [本文引用: 1]

The impact of phase-locked loop (PLL) parameters on the dynamic and steady-state behavior of a voltage-source converter (VSC) in an HVDC transmission system is determined as a function of the system strength [parameterized by the short-circuit ratio (SCR)]. This is achieved by using a linearized small-signal model of the converter system and its controls. The model is validated via electromagnetic transients simulation of the fully detailed large signal model. An interesting result from this study is that the maximum power transfer capability of the VSC-HVDC converter is affected by the PLL gains, and that the theoretical limit (obtained from static voltage stability analysis) is approachable as the PLL gains become very small. This paper shows that gains of the PLL, particularly at low SCRs, greatly affect the operation of the VSC-HVDC converter and that operation at low SCRs approaching 1.3 is very difficult.

辛焕海, 章枫, 于洋 , 等.

多馈入直流系统广义短路比:定义与理论分析

[J]. 中国电机工程学报, 2016,36(3):633-647.

[本文引用: 1]

Xin Huanhai, Zhang Feng, Yu Yang , et al.

Generalized short circuit ratio for multi-infeed DC systems:definition and theoretical analysis

[J]. Proceedings of the CSEE, 2016,36(3):633-647.

[本文引用: 1]

Roinila T, Messo T, Santi E .

MIMO identification techniques for rapid impedance-based stability assessment of three phase systems in dq domain

[J]. IEEE Transactions on Power Electronics, 2017(99):1.

[本文引用: 1]

张兴, 余畅舟, 刘芳 , 等.

光伏并网多逆变器并联建模及谐振分析

[J]. 中国电机工程学报, 2014: 34(3):336-345.

DOI:10.13334/j.0258-8013.pcsee.2014.03.003      URL     Magsci     [本文引用: 1]

针对光伏并网发电系统中多逆变器并联谐振问题, 首先, 建立包括电流控制、电压前馈和脉宽调制(pulse width modulation, PWM)谐波特性的单台逆变器小信号电路模型, 并扩展成多逆变器并联小信号模型, 提出基于2台逆变器和同类激励源合并的多逆变器并联系统小信号模型简化等效方法, 分析多逆变器的基本谐振特性, 并得出谐振与各逆变器控制和载波同步性有关的结论。最后, 通过相关的实验研究, 验证了所提出的多逆变器简化等效模型和理论分析的正确性。

Zhang Xing, Yu Changzhou, Liu Fang , et al.

Modeling and resonance analysis of multi-paralleled grid-tied inverters in PV systems

[J]. Proceedings of the CSEE, 2014: 34(3):336-345.

DOI:10.13334/j.0258-8013.pcsee.2014.03.003      URL     Magsci     [本文引用: 1]

针对光伏并网发电系统中多逆变器并联谐振问题, 首先, 建立包括电流控制、电压前馈和脉宽调制(pulse width modulation, PWM)谐波特性的单台逆变器小信号电路模型, 并扩展成多逆变器并联小信号模型, 提出基于2台逆变器和同类激励源合并的多逆变器并联系统小信号模型简化等效方法, 分析多逆变器的基本谐振特性, 并得出谐振与各逆变器控制和载波同步性有关的结论。最后, 通过相关的实验研究, 验证了所提出的多逆变器简化等效模型和理论分析的正确性。

/

〈 〉