1 引言
目前我国的MW级风电机组均采用了变桨技术。变桨是指风机可以沿桨叶的纵轴旋转叶片,使叶片的功角在一定范围(0°~90°)变化。改变桨叶位置,控制风轮的能量吸收,使风机保持一定的输出功率,在紧急情况下动作顺桨,减少风机载荷或实现空气制动[1 ] 。相比定桨距技术,变桨技术使得风机功率得到优化,可以更好地将风能转化为电能。
变桨系统作为大型风电机组控制系统的核心部分之一,对机组的安全、稳定、高效运行具有十分重要的作用。稳定的变桨控制已成为当前大型风力发电机组控制技术研究的热点和难点之一[2 ] 。
本文从控制模型入手,基于Matlab Simulink搭建了系统仿真模型,通过将变桨控制系统各子部分数字模型化,从风机位置指令到速度指令,再到电流指令,最后经过伺服驱动控制电机,使桨叶转到相应的位置。
2 变桨系统结构与基本原理
变桨距风力机通过调节风力机桨距角来改变叶片的风能捕获能力,进而调节风力机的输出功率。当风速低于额定风速时,保持风力机桨距角恒定,通过发电机调速控制使风力机运行于最佳叶尖速,维持风力机组在最佳风能捕获效率下运行。轮毂主控制器根据当前风速确定桨叶待调整位置,并将位置指令下发给变桨控制系统。
变桨系统按执行机构进行分类主要有两种,即液压变桨系统和电动变桨系统,在控制方式上可分为三叶片统一变桨和独立变桨两种[1 ] 。本文主要介绍目前主流的独立电动变桨系统。
电动变桨系统是典型的位置伺服控制系统,通过伺服驱动器控制电动机旋转,电动机带动减速齿轮箱的输出轴齿轮旋转,输出轴齿轮与桨叶根部回转支承的内侧齿轮啮合,从而带动桨叶进行变桨。变桨系统通常主要由后备电源、伺服电机、减速齿轮箱、伺服驱动、轮毂主控制器和传感器等组成。当外部电源供电故障时,后备电源投入使用,为变桨驱动器供电,以确保桨叶能够紧急顺桨。目前主流的后备电源由超级电容替代了过去常用的铅酸电池。
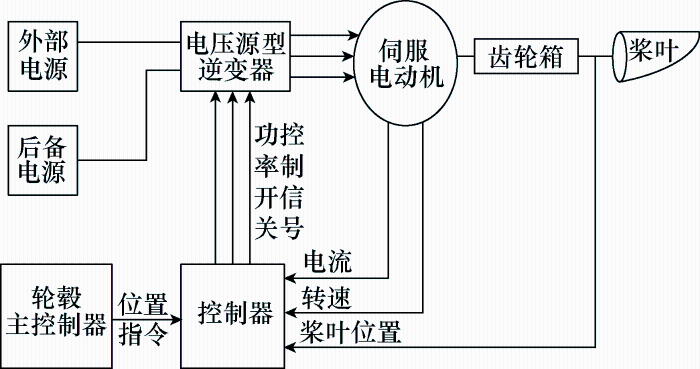
图1 为变桨系统结构框图。变桨控制器接收轮毂主控制器的位置指令,以及传感器测量的电流、速度和位置信号,经分析运算后给出变桨电机的速度或位置信号。减速齿轮箱将电机的高速、小转矩运动转为桨叶的低速、大转矩运动。
图1
3 变桨控制系统动态数学模型
构成变桨控制系统的主要环节包括伺服电动机,伺服驱动器、调节器和滤波器。本文以永磁同步电动机作为控制对象,以各模块的传递函数和动态结构图来表示变桨控制系统的数学模型。
3.1 PMSM模型
永磁同步电动机(Permanent magnet synchronous machine,PMSM)具有结构简单、体积小、重量轻、损耗小等优点,在大功率风力发电技术中有着广泛的应用[3 ] 。
假定永磁同步电动机具有定子三项分布绕组和永磁转子,忽略铁心饱和,不计涡流和磁滞损耗,转子上无阻尼绕组,永磁体不计阻尼作用[4 ] ,${{L}_{d}}={{L}_{q}}=L$。采用${{i}_{d}}=0$转子磁链定向控制,在$dq$同步旋转坐标下PMSM的磁链方程为[5 ]
(1) $\left\{ \begin{align} & {{\psi }_{d}}={{\psi }_{\text{r}}} \\ & {{\psi }_{q}}=L{{i}_{q}} \\ \end{align} \right.$
(2) $\left\{ \begin{align} & {{u}_{d}}=-{{\omega }_{1}}{{\psi }_{q}} \\ & {{u}_{q}}=R{{i}_{q}}+L\frac{\text{d}{{i}_{q}}}{\text{d}t}+{{\omega }_{1}}{{\psi }_{d}} \\ \end{align} \right.$
(3) ${{T}_{\text{e}}}=K{{i}_{q}}$
式中,${{u}_{d}}{{u}_{q}}$为$dq$轴电压;${{\psi }_{d}}{{\psi }_{q}}$为$dq$轴磁链;${{i}_{d}}{{i}_{q}}$为$dq$轴电流;${{\omega }_{1}}$为电机电角速度;$RL$为定子绕组电阻、电感;${{T}_{\text{e}}}$为电磁转矩;$K$为与电机极对数和转子磁链有关的常数。
由于转子磁链恒定,因此电磁转矩与定子电流的幅值成正比,控制定子电流就能很好地控制转矩,与直流电动机完全相同[6 ] 。借助直流电动机的模型,得出采用${{i}_{d}}=0$转子磁链定向控制,在dq 同步旋转坐标下永磁同步电机模型[6 ] 为
(4) ${{G}_{\text{PMSM1}}}(s)=\frac{{{I}_{q}}(s)}{{{U}_{d}}(s)-E(s)}=\frac{1/R}{{{T}_{\text{l}}}s+1}$
(5) ${{G}_{\text{PMSM2}}}(s)=\frac{E(s)}{{{I}_{q}}(s)-I_{qL}^{{}}(s)}=\frac{R}{{{T}_{\text{m}}}s}$
(6) ${{C}_{\text{e}}}=\frac{{{U}_{\text{N}}}-{{I}_{\text{N}}}{{R}_{\text{a}}}}{{{n}_{\text{N}}}}$
(7) ${{T}_{\text{l}}}=\frac{L}{R}$
(8) ${{T}_{\text{m}}}=\frac{G{{D}^{2}}R}{375{{C}_{\text{e}}}{{C}_{\text{m}}}}=\frac{4gJR}{375{{C}_{\text{e}}}{{C}_{\text{m}}}}=\frac{RJ}{{{K}_{\text{e}}}{{K}_{\text{t}}}}$
(9) ${{C}_{\text{m}}}=\frac{30}{\text{ }\!\!\pi\!\!\text{ }}{{C}_{\text{e}}}$
(10) ${{I}_{q\text{L}}}=\frac{{{T}_{\text{L}}}}{{{C}_{\text{m}}}}$
式中,${{T}_{\text{L}}}$为包括电动机空载转矩在内的负载转矩;$G{{D}^{2}}$为电力拖动系统折算到电动机轴上的飞轮惯量;${{C}_{\text{m}}}$为额定励磁下电动机的转矩系数;${{C}_{\text{e}}}$为电枢回路电磁时间常数;${{T}_{\text{m}}}$为电力拖动系统机电时间常数;${{I}_{q\text{L}}}$为负载电流。
3.2 伺服驱动器模型
伺服驱动一般采用电压源型逆变器,空间矢量调制(SVPWM)具有控制范围大、谐波畸变小和瞬态响应等优点[7 ] 。基于SVPWM算法控制的电压源型逆变器可近似等效为一阶惯性环节,即
(11) ${{G}_{I\text{NV}}}(s)=\frac{{{K}_{\text{s}}}}{{{T}_{\text{s}}}s+1}$
式中,${{T}_{\text{s}}}$为逆变器延迟时间,一般小于等于开关频率周期[6 ] 。因逆变器与输出给定电压相等,故为单位增益,${{K}_{\text{s}}}=1$[4 ] 。
3.3 滤波器模型
为了抑制高频噪声对电流环和速度环的干扰[8 ] ,通常对电流和速度采样值作数字低通滤波,分别等效为一阶惯性环节,即
(12) ${{G}_{\text{CF}}}(s)=\frac{1}{{{T}_{\text{CF}}}s+1}$
(13) ${{G}_{\text{SF}}}(s)=\frac{1}{{{T}_{\text{SF}}}s+1}$
3.4 调节器模型
变桨控制系统由位置环、速度环和电流环三环构成。三闭环调速系统中设置了三个调节器,即位置调节器(Automatic position regulator,APR)、转速调节器(Automatic speed regulator,ASR)和电流调节器(Automatic current regulator,ACR),分别引入位置负反馈、转速负反馈和电流负反馈[9 ] 。
为了实现快速、精准、可靠的控制,位置环、速度环和电流环均采用经典PI结构,数学模型为
(14) ${{G}_{\text{APR}}}(s)={{k}_{\text{pp}}}+\frac{{{k}_{\text{pi}}}}{s}$
(15) ${{G}_{\text{ASR}}}(s)={{k}_{\text{sp}}}+\frac{{{k}_{\text{si}}}}{s}$
(16) ${{G}_{\text{ACR}}}(s)={{k}_{\text{cp}}}+\frac{{{k}_{\text{ci}}}}{s}$
4 变桨控制系统动态结构框图
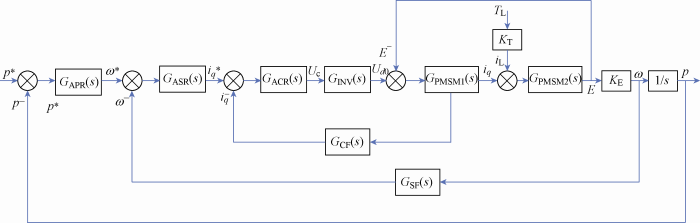
图2 为变桨控制系统动态结构框图,各模型表达式见前文,其中${{K}_{\text{T}}}$和${{K}_{\text{E}}}$为两个电机常数[6 ] 计算式为
(17) ${{K}_{\text{T}}}=\frac{1}{{{C}_{\text{m}}}}$
(18) ${{K}_{\text{E}}}=\frac{1}{{{C}_{\text{e}}}}\frac{\text{ }\!\!\pi\!\!\text{ }}{30}$
图2
除了各调节器输出值要考虑限幅,为了变桨系统的安全运行,需要设定桨叶侧加速度限幅,目前一般采用分段式S曲线加速度限幅法[10 ] ,具体分段以及加速度值根据实际情况确定。
除了功率器件本身的延时时间,还需考虑各通信部件双向通信延时时间[11 ] 。
5 变桨控制系统仿真
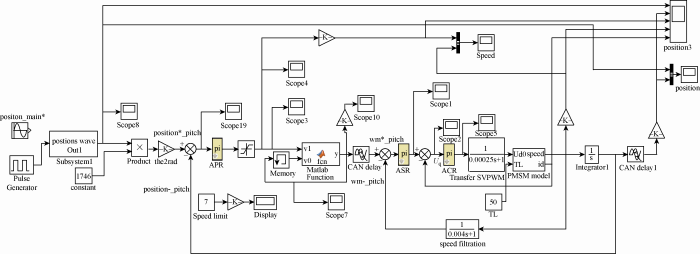
为了验证以上模型的正确性,特选取实际变桨系统17.1 kW电机作为控制对象,在Matlab Simulink中搭建了风电变桨控制系统仿真模型,如图3 所示。
图3
仿真电机参数见表1 ,将电机参数代入模型公式,经计算得:${{T}_{\text{L}}}={{0.036}_{{}}}2$,${{T}_{\text{m}}}={{0.001}_{{}}}7$,${{C}_{\text{e}}}={{0.110}_{{}}}3$,${{C}_{\text{m}}}={{0.153}_{{}}}9$。
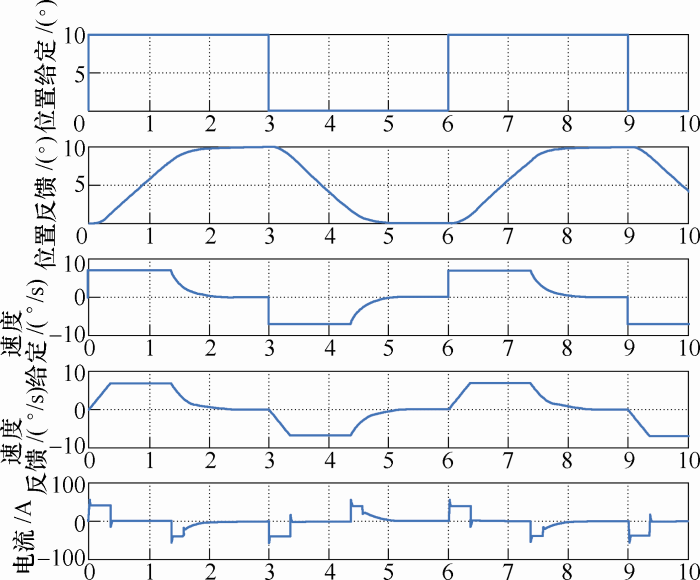
给定阶跃信号矩形波如图4 所示,为了更直观地观察电机加速减速过程,本仿真设定最大加速度20 °/s2 ,速度限制7 °/s。
图4
通过算例分析变桨系统的动态性能。在系统起动过程中转速调节器经历了不饱和、饱和、退饱和三种情况,整个起动过程可以分为电流上升阶段、恒流升速阶段和转速调节阶段。在调节器的作用下,电机以最大加速度加速到7 °/s后维持最大速度运行再减速,直到到达给定位置。
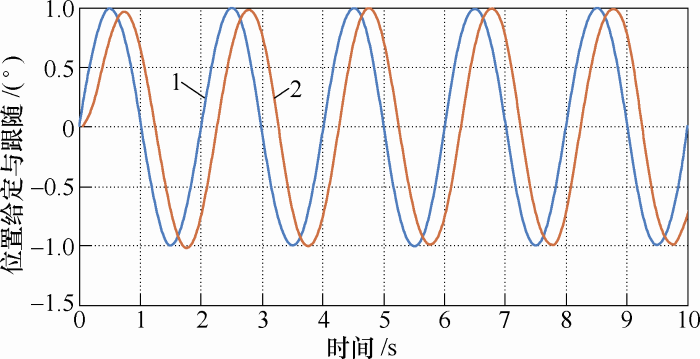
给定1°、0.5 Hz正弦波如图5 所示,空载,测试变桨系统位置跟随情况。图中曲线1为给定位置指令,曲线2为位置跟随曲线。仿真结果表明位置幅值没有衰减,相位滞后12.5%。根据实际工况调整调节器的${{K}_{\text{p}}}{{K}_{\text{i}}}$参数,可以实现幅值和相位的不同跟随状态。
图5
6 结论
本文从变桨控制系统各部分的数学模型入手,基于Matlab Simulink搭建了变桨控制系统的动态仿真模型,从风机位置指令到速度指令,再到电流指令,最后经过伺服驱动控制电机,使桨叶转到相应的位置。介绍了一种研究变桨系统控制原理的方法,通过给定阶跃和周期正弦波指令,对电机的加减速以及位置跟随进行仿真,仿真过程的调试与研究对实际系统参数调试以及现象分析有着重要的指导意义。
参考文献
View Option
[1]
丛智慧 . 风电机组变桨系统原理与维护
[J]. 内蒙古科技与经济 , 2016 (18 ):77 -79 .
[本文引用: 2]
Cong Zhihui . Principle and maintenance of wind turbine propeller control system
[J]. Inner Mongolia Science Technology & Economy , 2016 (18 ):77 -79 .
[本文引用: 2]
[2]
胡国强 . 风力发电机组变桨系统的设计
[J]. 机电工程 , 2012 ,29 (5 ):588 -592 .
[本文引用: 1]
Hu Guoqiang . Design of wind power generators change oars system
[J]. Journal of Mechanical & Electrical Engineering , 2012 ,29 (5 ):588 -592 .
[本文引用: 1]
[3]
暨绵浩 . 永磁同步电动机及其调速系统综述和展望
[J]. 微特电机 , 2007 (3 ):49 -52 .
[本文引用: 1]
Ji Mianhao . Summarize and prospect of the PMSM system of frequency-conversion and timing
[J]. Small & Special Electrical Machines , 2007 (3 ):49 -52 .
[本文引用: 1]
[4]
王莉娜 , 朱鸿悦 , 杨宗军 . 永磁同步电动机调速系统PI控制器参数整定方法
[J]. 电工技术学报 , 2014 ,29 (5 ):104 -116 .
[本文引用: 2]
Wang Lina Zhu Hongyue Yang Zongjun . Tuning method for PI controllers of PMSM driving system
[J]. Transactions of China Electrotechnical Society , 2014 ,29 (5 ):104 -116 .
[本文引用: 2]
[5]
王莉娜 , 杨宗军 . Simulink 中永磁同步电机模型的改进和应用
[J]. 电机与控制学报 , 2012 ,16 (7 ):77 -82 .
[本文引用: 1]
Wang Lina Yang Zongjun . PMSM model’s reform in Simulink and application in parameters’ identification
[J]. Electric Machines and Control , 2012 ,16 (7 ):77 -82 .
[本文引用: 1]
[6]
陈伯时 . 电力拖动自动控制系统 [M]. 北京 : 机械工业出版社 , 2005 .
[本文引用: 4]
[7]
Tang Wei Huang Junmei Wu Jie et al . A PID tuning method based on dominant poles and phase margin
[C]. Proceedings of the 29th Chinese Control Conference , 2010 : 3402 -3405 .
[本文引用: 1]
[8]
黄樟坚 , 李辉 , 刘行中 , 等 . 风电变桨系统模型简化及运行特性比较
[J]. 电测与仪表 , 2018 ,55 (1 ):65 -71 .
[本文引用: 1]
Huang Zhangjian Li Hui Liu Xingzhong , et al . Simplification of wind turbine pitch system and comparison of operating characteristics
[J]. Electrical Measurement & Instrumentation , 2018 ,55 (1 ):65 -71 .
[本文引用: 1]
[9]
李辉 , 杨超 , 赵斌 , 等 . 风电机组电动变桨系统建模及运行特性评估与测试
[J]. 电力系统自动化 , 2013 ,37 (11 ):20 -25 .
[本文引用: 1]
Li Hui Yang Chao Zhao Bin , et al . Modeling and operation characteristic evaluation and testing of electric propeller system for wind turbine units
[J]. Automation of Electric Power Systems , 2013 ,37 (11 ):20 -25 .
[本文引用: 1]
[10]
朱磊 , 朱元 . 基于S曲线的永磁同步电机加减速控制及算法分析研究
[J]. 数字技术与应用 , 2013 (4 ):155 -156 .
[本文引用: 1]
Zhu Lei Zhu Yuan . Acceleration and speed control of PMSM based on S-curve
[J]. Digital Technology & Application , 2013 (4 ):155 -156 .
[本文引用: 1]
[11]
贺明智 , 许建平 , 游小杰 , 等 . 环路延时对数字峰值电压控制开关变换器瞬态性能的影响
[J]. 中国电机工程学报 , 2009 ,29 (6 ):1 -7 .
URL
Magsci
[本文引用: 1]
<p>研究数字控制环路延时对开关变换器瞬态性能的影响,提出克服环路延时影响的简单实用算法。在数字峰值电压算法的基础上,对开关变换器数字控制算法中延时的存在进行分析,提出克服延时的策略,并得到改进型数字峰值电压控制算法。在此基础上,对单次采样的局限性进行分析,并提出将多采样算法用于典型降压(Buck)变换器中,用于进一步减小环路延时。利用仿真和实验对所提出的不同算法进行验证,并对瞬态性能进行分析。结果比较说明采用克服延时算法能减小延时,从而提高瞬态响应,多采样算法则是在此基础上的进一步改进。</p>
He Mingzhi Xu Jianping You Xiaojie , et al . Time delay effect on transient performance of digital peak voltage controlled switching converter
[J]. Proceedings of the CSEE , 2009 ,29 (6 ):1 -7 .
URL
Magsci
[本文引用: 1]
<p>研究数字控制环路延时对开关变换器瞬态性能的影响,提出克服环路延时影响的简单实用算法。在数字峰值电压算法的基础上,对开关变换器数字控制算法中延时的存在进行分析,提出克服延时的策略,并得到改进型数字峰值电压控制算法。在此基础上,对单次采样的局限性进行分析,并提出将多采样算法用于典型降压(Buck)变换器中,用于进一步减小环路延时。利用仿真和实验对所提出的不同算法进行验证,并对瞬态性能进行分析。结果比较说明采用克服延时算法能减小延时,从而提高瞬态响应,多采样算法则是在此基础上的进一步改进。</p>
风电机组变桨系统原理与维护
2
2016
... 目前我国的MW级风电机组均采用了变桨技术.变桨是指风机可以沿桨叶的纵轴旋转叶片,使叶片的功角在一定范围(0°~90°)变化.改变桨叶位置,控制风轮的能量吸收,使风机保持一定的输出功率,在紧急情况下动作顺桨,减少风机载荷或实现空气制动[1 ] .相比定桨距技术,变桨技术使得风机功率得到优化,可以更好地将风能转化为电能. ...
... 变桨系统按执行机构进行分类主要有两种,即液压变桨系统和电动变桨系统,在控制方式上可分为三叶片统一变桨和独立变桨两种[1 ] .本文主要介绍目前主流的独立电动变桨系统. ...
风电机组变桨系统原理与维护
2
2016
... 目前我国的MW级风电机组均采用了变桨技术.变桨是指风机可以沿桨叶的纵轴旋转叶片,使叶片的功角在一定范围(0°~90°)变化.改变桨叶位置,控制风轮的能量吸收,使风机保持一定的输出功率,在紧急情况下动作顺桨,减少风机载荷或实现空气制动[1 ] .相比定桨距技术,变桨技术使得风机功率得到优化,可以更好地将风能转化为电能. ...
... 变桨系统按执行机构进行分类主要有两种,即液压变桨系统和电动变桨系统,在控制方式上可分为三叶片统一变桨和独立变桨两种[1 ] .本文主要介绍目前主流的独立电动变桨系统. ...
风力发电机组变桨系统的设计
1
2012
... 变桨系统作为大型风电机组控制系统的核心部分之一,对机组的安全、稳定、高效运行具有十分重要的作用.稳定的变桨控制已成为当前大型风力发电机组控制技术研究的热点和难点之一[2 ] . ...
风力发电机组变桨系统的设计
1
2012
... 变桨系统作为大型风电机组控制系统的核心部分之一,对机组的安全、稳定、高效运行具有十分重要的作用.稳定的变桨控制已成为当前大型风力发电机组控制技术研究的热点和难点之一[2 ] . ...
永磁同步电动机及其调速系统综述和展望
1
2007
... 永磁同步电动机(Permanent magnet synchronous machine,PMSM)具有结构简单、体积小、重量轻、损耗小等优点,在大功率风力发电技术中有着广泛的应用[3 ] . ...
永磁同步电动机及其调速系统综述和展望
1
2007
... 永磁同步电动机(Permanent magnet synchronous machine,PMSM)具有结构简单、体积小、重量轻、损耗小等优点,在大功率风力发电技术中有着广泛的应用[3 ] . ...
永磁同步电动机调速系统PI控制器参数整定方法
2
2014
... 假定永磁同步电动机具有定子三项分布绕组和永磁转子,忽略铁心饱和,不计涡流和磁滞损耗,转子上无阻尼绕组,永磁体不计阻尼作用[4 ] ,${{L}_{d}}={{L}_{q}}=L$.采用${{i}_{d}}=0$转子磁链定向控制,在$dq$同步旋转坐标下PMSM的磁链方程为[5 ] ...
... 式中,${{T}_{\text{s}}}$为逆变器延迟时间,一般小于等于开关频率周期[6 ] .因逆变器与输出给定电压相等,故为单位增益,${{K}_{\text{s}}}=1$[4 ] . ...
永磁同步电动机调速系统PI控制器参数整定方法
2
2014
... 假定永磁同步电动机具有定子三项分布绕组和永磁转子,忽略铁心饱和,不计涡流和磁滞损耗,转子上无阻尼绕组,永磁体不计阻尼作用[4 ] ,${{L}_{d}}={{L}_{q}}=L$.采用${{i}_{d}}=0$转子磁链定向控制,在$dq$同步旋转坐标下PMSM的磁链方程为[5 ] ...
... 式中,${{T}_{\text{s}}}$为逆变器延迟时间,一般小于等于开关频率周期[6 ] .因逆变器与输出给定电压相等,故为单位增益,${{K}_{\text{s}}}=1$[4 ] . ...
Simulink 中永磁同步电机模型的改进和应用
1
2012
... 假定永磁同步电动机具有定子三项分布绕组和永磁转子,忽略铁心饱和,不计涡流和磁滞损耗,转子上无阻尼绕组,永磁体不计阻尼作用[4 ] ,${{L}_{d}}={{L}_{q}}=L$.采用${{i}_{d}}=0$转子磁链定向控制,在$dq$同步旋转坐标下PMSM的磁链方程为[5 ] ...
Simulink 中永磁同步电机模型的改进和应用
1
2012
... 假定永磁同步电动机具有定子三项分布绕组和永磁转子,忽略铁心饱和,不计涡流和磁滞损耗,转子上无阻尼绕组,永磁体不计阻尼作用[4 ] ,${{L}_{d}}={{L}_{q}}=L$.采用${{i}_{d}}=0$转子磁链定向控制,在$dq$同步旋转坐标下PMSM的磁链方程为[5 ] ...
4
2005
... 由于转子磁链恒定,因此电磁转矩与定子电流的幅值成正比,控制定子电流就能很好地控制转矩,与直流电动机完全相同[6 ] .借助直流电动机的模型,得出采用${{i}_{d}}=0$转子磁链定向控制,在dq 同步旋转坐标下永磁同步电机模型[6 ] 为 ...
... [6 ]为 ...
... 式中,${{T}_{\text{s}}}$为逆变器延迟时间,一般小于等于开关频率周期[6 ] .因逆变器与输出给定电压相等,故为单位增益,${{K}_{\text{s}}}=1$[4 ] . ...
... 图2 为变桨控制系统动态结构框图,各模型表达式见前文,其中${{K}_{\text{T}}}$和${{K}_{\text{E}}}$为两个电机常数[6 ] 计算式为 ...
A PID tuning method based on dominant poles and phase margin
1
2010
... 伺服驱动一般采用电压源型逆变器,空间矢量调制(SVPWM)具有控制范围大、谐波畸变小和瞬态响应等优点[7 ] .基于SVPWM算法控制的电压源型逆变器可近似等效为一阶惯性环节,即 ...
风电变桨系统模型简化及运行特性比较
1
2018
... 为了抑制高频噪声对电流环和速度环的干扰[8 ] ,通常对电流和速度采样值作数字低通滤波,分别等效为一阶惯性环节,即 ...
风电变桨系统模型简化及运行特性比较
1
2018
... 为了抑制高频噪声对电流环和速度环的干扰[8 ] ,通常对电流和速度采样值作数字低通滤波,分别等效为一阶惯性环节,即 ...
风电机组电动变桨系统建模及运行特性评估与测试
1
2013
... 变桨控制系统由位置环、速度环和电流环三环构成.三闭环调速系统中设置了三个调节器,即位置调节器(Automatic position regulator,APR)、转速调节器(Automatic speed regulator,ASR)和电流调节器(Automatic current regulator,ACR),分别引入位置负反馈、转速负反馈和电流负反馈[9 ] . ...
风电机组电动变桨系统建模及运行特性评估与测试
1
2013
... 变桨控制系统由位置环、速度环和电流环三环构成.三闭环调速系统中设置了三个调节器,即位置调节器(Automatic position regulator,APR)、转速调节器(Automatic speed regulator,ASR)和电流调节器(Automatic current regulator,ACR),分别引入位置负反馈、转速负反馈和电流负反馈[9 ] . ...
基于S曲线的永磁同步电机加减速控制及算法分析研究
1
2013
... 除了各调节器输出值要考虑限幅,为了变桨系统的安全运行,需要设定桨叶侧加速度限幅,目前一般采用分段式S曲线加速度限幅法[10 ] ,具体分段以及加速度值根据实际情况确定. ...
基于S曲线的永磁同步电机加减速控制及算法分析研究
1
2013
... 除了各调节器输出值要考虑限幅,为了变桨系统的安全运行,需要设定桨叶侧加速度限幅,目前一般采用分段式S曲线加速度限幅法[10 ] ,具体分段以及加速度值根据实际情况确定. ...
环路延时对数字峰值电压控制开关变换器瞬态性能的影响
1
2009
... 除了功率器件本身的延时时间,还需考虑各通信部件双向通信延时时间[11 ] . ...
环路延时对数字峰值电压控制开关变换器瞬态性能的影响
1
2009
... 除了功率器件本身的延时时间,还需考虑各通信部件双向通信延时时间[11 ] . ...