1 引言
偏心的相关研究主要包括内部和外部。 偏心的外部分析对象是定子电流信号、转矩信号等。许多文献对偏心问题进行了研究。文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎。快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具。希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点。偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题。
文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果。最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式。不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究。然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂。另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼。定子绕组设置成多并联支路数也会限制UMP的大小[8 ] 。
过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声。电机的振动与噪声研究一直以来是比较热门的方向。文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较。文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声。文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波。应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型。文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声。文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声。文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声。文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加。
虽然有关偏心研究的文献有很多,但有关弧偏心(实际)[14 ] 的研究却很少。本文进行了弧偏心的基础研究,首次从力学角度研究弧偏心的整个过程,详细分析产生弧形挠度的主要原因。主要内容分三部分:首先是重力部分。如果没有重力并且材料的弹性模量属性不存在,离心力和不平衡磁拉力也就不需要讨论了;第二部分是离心力部分。当存在挠度时,离心力就会一直存在;第三部分是不平衡磁拉力。当电机转子出现较大挠度时,转子所受的不平衡磁拉力会很大。另外,根据研究,不平衡磁拉力是一个有关时间的函数。
本文以一台1.2 MW, 6 kV, 4极的感应电机作为研究对象,主要目的是计算总挠度。为了准确计算不平衡磁拉力,建立了感应电机的2D有限元模型,并采用有限元软件Ansoft Maxwell进行仿真计算。
2 挠度计算
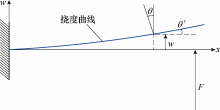
在材料力学中,弯曲的轴叫做挠度曲线,如图1 所示。研究表明,剪切力对其变形的影响一般可以忽略不计,而认为变形后横截面仍保持平面。
图1
(1) $\theta \approx \tan \theta =\frac{\text{d}w}{\text{d}x}$
在建立纯弯曲正应力公式时,得到用中性层曲率表示的弯曲变形为
(2) $\frac{1}{\rho }=\frac{M}{EI}$
如果忽略剪切力对梁变形的影响,式(2)也可用于一般非纯弯曲。在这种情况下,由于弯矩M 与曲率半径ρ 均为x 的函数,式(2)可变为
(3) $\frac{1}{\rho(x)}=\frac{M(x)}{EI}$
(4) $\frac{1}{\rho(x)}=\frac{\tfrac{{{\text{d}}^{2}}w}{\text{d}{{x}^{2}}}}{{{\left[ 1+{{\left( \tfrac{\text{d}w}{\text{d}x} \right)}^{2}} \right]}^{3/2}}}$
由于梁的转角一般非常小,因此(dw /dx )2 远小于1,所以式(4)可以简化为
(5) $\frac{{{\text{d}}^{2}}w}{\text{d}{{x}^{2}}}=\frac{M(x)}{EI}$
在感应电机中,为了准确分析,风扇结构的轴向长度也应考虑在内。风扇结构的使用是为了增加风的流动性。因此,应当考虑风扇的重量。在误差允许的情况下为使模型更简单,风扇的重量记在硅钢片当中。阶梯化的转子轴也被简化为一个圆柱体的轴。
(6) $\theta = \frac{\text{d}w}{\text{d}x}=\int{\frac{M(x)}{EI}\text{d}x}+{{k}_{1}}$
(7) $w=\iint{\frac{M(x)}{EI}}\text{d}x\text{d}x+{{k}_{1}}x+{{k}_{2}}$
当弯矩方程需要分段建立或弯曲刚度沿梁轴变化,以致其表达式需要分段建立时,挠曲轴近似微分方程也需要分段建立,而在各段的积分中,将分别包含两个积分常数。为了确定这些常数,除应利用位移边界条件外,还应利用分段处挠曲轴的连续、光滑条件。因为在相邻段的交接处,相连两截面应具有相同的挠度与转角。
2.1 重力引起的挠度计算
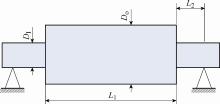
实际上,电机转子在静态分析中不是理想的杆。它通常由45钢轴、硅钢片以及铝导条组成。此外,大电机中的转子通常是细长结构。也就是说转子上存在重力导致变形弯曲。虽然钢的硬度很大,但转子较长难以承受巨大的弯矩。在大电机中,转子的重力分析尤为重要。
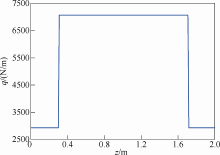
本文采用的大电机型转子实物如图2 所示,电机相关参数见下表。转子的重力分为两种均匀载荷。根据表中的参数,轴的载荷q shaft = 2.924 36 kN/m,硅钢片部分的载荷q sss = 4.140 03 kN/m。其轴上的载荷分布曲线如图3 所示。考虑到两种材料弹性模量不一样,本文采用叠加法方便计算。首先,针对施加在轴上的均匀载荷,根据工程力学知识,得到挠度表达式为
(8) ${{w}_{1}}=-2.025\times {{10}^{-10}}z(2l{{z}^{2}}-{{z}^{3}}-{{l}^{3}})$
图2
按表中的电机参数,相应转子及轴的简化示意图如图3 所示。
图3
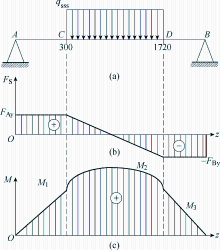
其次分析硅钢片的部分。通过力学分析,发现弯矩M (z )被分成三部分,如图4 所示。将弯矩M (z )代入挠曲轴近似微分方程中,根据计算,M (z )和w 2 的表达式分别为
$\left\{ \begin{align} & {{M}_{1}}={{2}_{{}}}{{910.030}_{{}}}75z\text{ }0\le z<0.3 \\ & {{M}_{2}}=-{{2}_{{}}}{{070.017}_{{}}}606{{z}^{2}}+{{4}_{{}}}{{152.041}_{{}}}313z- \\ & \text{ }\ \ \ {{186.301}_{{}}}{{584}_{{}}}4\text{ }0.3\le z<1.72 \\ & {{M}_{3}}=-{{2}_{{}}}{{968.819}_{{}}}25z+{{5}_{{}}}{{937.638}_{{}}}5 \\ & \text{ }1.72\le z\le 2 \\ \end{align} \right.$
$\left\{ \begin{align} & EI{{w}_{2}}={{485.005}_{{}}}125{{z}^{3}}+Cz\text{ }0\le z<0.3 \\ & EI{{w}_{2}}=-{{172.501}_{{}}}{{467}_{{}}}2{{z}^{4}}+{{692.006}_{{}}}{{885}_{{}}}5{{z}^{3}}- \\ & \text{ }\ \ \ \ {{93.150}_{{}}}{{792}_{{}}}2{{z}^{2}}-{{1}_{{}}}{{205.210}_{{}}}831z+D \\ & \text{ }0.3\le z<1.72 \\ & EI{{w}_{2}}=-{{494.803}_{{}}}{{208}_{{}}}3{{z}^{3}}+{{2}_{{}}}{{968.819}_{{}}}25{{z}^{2}}+ \\ & \ \ Ez+{{7}_{{}}}{{916.851}_{{}}}333-2E\text{ }1.72\le z\le 2 \\ \end{align} \right.$
图4
因为本文只关注电磁区域,因此忽略某些未知常数并不影响研究。即本文只关注w 2 在z ∈[0.3,1.72]区间。综上所述,已知挠度曲线的形状,其上下偏差还缺少条件。
(9) ${{w}_{\text{G}}}=(-\text{3}\text{.20}{{\text{4}}_{{}}}\text{73}{{\text{7}}_{{}}}\text{212 }{{z}^{4}}+\text{12}\text{.83}{{\text{2}}_{{}}}\text{63}{{\text{1}}_{{}}}\text{02}{{z}^{3}}-{{0.636}_{{}}}{{928}_{{}}}{{493}_{{}}}7{{z}^{2}}-\text{24}\text{.44}{{\text{2}}_{{}}}\text{67}{{\text{7}}_{{}}}\text{82}z)\times {{10}^{-10}}+\varepsilon $
通过简化模型核算,可得ε = 7.2×10-10 。考虑到材料疲劳以及计算误差,假设|wG |max =1%δ ,则ε =1.99×10-5 。从表达式系数可以看出,弯曲的角度非常小。图5 给出其力学分析。其中F s 为横截面的剪切力;M 为弯矩。
图5
2.2 离心力计算
离心力是一种惯性力,它使旋转的物体远离它的旋转中心。在牛顿力学里,离心力曾被用于表述两个不同的概念:在一个非惯性参考系下观测到的一种惯性力;向心力的平衡。在拉格朗日力学中,离心力有时被用来描述在某个广义坐标下的广义力。在通常意义下,离心力并不是真实存在的力。它的作用只是为了在旋转参考系(非惯性参考系)下,牛顿运动定律依然能够使用。
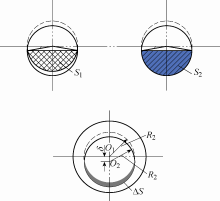
由于转子重力所引起的挠度,转子上的离心力在重力方向上不平衡。尽管偏离的质量不大,鉴于转速较高,离心力不能忽略不计。电机横截面示意图如图6 所示。
图6
(10) $\Delta S={{S}_{2}}-{{S}_{1}}$
(11) $\Delta S=\left( \tfrac{{{r}^{2}}}{2\text{ }\!\!\pi\!\!\text{ }}+\sqrt{{{r}^{2}}-{{\delta }^{2}}} \right)\delta $
仅考虑挠度w G 所引起的离心力。视w G (z )为δ (z )。因此,偏离体积为
(12) ${{V}_{\text{devi}}}=\int_{0.3}^{1.72}{\Delta S\text{d}z}$
(13) ${{F}_{\text{off}}}=m{{w}^{2}}r$
转子向心力载荷密度如图7 所示。从图7 可以看出离心力不能忽视,但与重力相比,其值不是很大。因此,为了简便计算,将离心力的作用简化为对w G 作修正。即
(14) $w{{'}_{\text{G}}}=(-\text{3}\text{.21 }{{z}^{4}}+\text{12}\text{.835}{{z}^{3}}-0.636{{z}^{2}}-\text{24}\text{.44}{{\text{2}}_{{}}}\text{6}z)\times {{10}^{-10}}+\varepsilon '$
图7
在偏心中,离心力总是存在。而且,随着更大的弯曲,离心力越大。其影响会大大改变其挠度并且严重时引起定转子相擦。
2.3 第三部分的计算
根据电磁场理论,电机中的磁场会引起磁吸力。由于气隙空间对称,健康的电机不存在不平衡磁拉力问题。当电机中发生偏心故障时,电机气隙空间分布不再对称,即空间的气隙磁阻不一样。那么磁吸力合力就不为0。这是产生UMP的原因。
为了计算电机的UMP,解析法用于表示弧偏心。电磁力是由交变的磁场产生的。所以,首先获得气隙磁通密度表达式。根据传统理论,气隙磁通密度表达式为
(15) $b\left( z,\theta ,\varphi \right)={{f}_{0}}\left( z,\theta ,\varphi \right)\frac{{{\mu }_{0}}}{\delta \left( z,\theta ,\varphi \right)}$
式中,f 0 (z , θ , φ )为磁动势;μ 0 为真空磁导率。
(16) $F(z,\theta ,\varphi )=\frac{{{b}^{2}}(z,\theta ,\varphi )}{2{{\mu }_{0}}}S$
UMP很难通过单一解析表达式来进行计算。因此,有限元计算被用于准确计算UMP。为了简化仿真计算,提高计算效率,在Ansoft Maxwell中建立2D仿真模型。
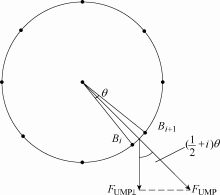
在弧偏心中,电机的每一个横截面都是动态偏心。对最大挠度处的2D动态偏心进行仿真。其中,圆周的计算点是有限的。
(17) ${{F}_{i(i+1)}}=\frac{1}{2{{\mu }_{0}}}{{\left( \frac{{{B}_{i}}+{{B}_{i+1}}}{2} \right)}^{2}}{{R}_{2}}\theta \cos \left[ \theta \left( i+\tfrac{1}{2} \right) \right]$
(18) ${{F}_{\text{S}}}=\sum\limits_{i}{{{F}_{i(i+1)}}}$
考虑到式(15),f 0 (z , θ , φ )幅值通常恒定,b (z , θ , φ )与δ (z , θ , φ )成反比关系。所以沿z 轴的圆周气隙磁通密度大致为
(19) ${{F}_{\text{S}}}(z)\propto \frac{1}{{{\delta }^{2}}(z,\theta ,\varphi )}$
(20) ${{F}_{\text{UMP}}}=\int_{0.3}^{1.72}{{{F}_{\text{S}}}\frac{{{\delta }^{2}}(z)}{\delta _{\max }^{2}}\text{d}z}$
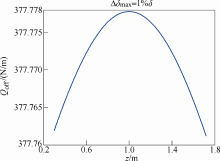
根据上述对△δ max =1%δ 的弧偏心进行的仿真数据,可以计算得到总UMP。由于转子一直转动,需要计算的沿转子弯曲方向上的UMP分量在较大范围内会有由正到负的变化。
4极电机的定转子间实际计算圆周曲线如图8 所示。其某时刻的气隙磁通密度图如图9 所示。从图中可以看出,由于仿真的偏心度很小,磁通密度的畸变很难由肉眼直接看出来。
图8
图9
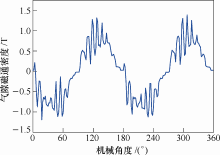
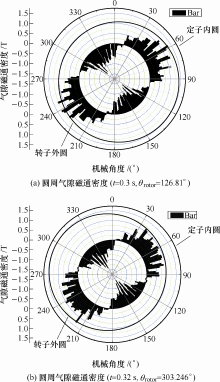
图10 为极坐标下的圆周气隙磁通密度。可以看出,类正弦波形波形的中心线与转子对称轴不平行。而且类正弦波形波形的中心线与转子对称轴的夹角在电机运转时总是在变化。根据感应电机原理,气隙磁动势与基波有关,其转速与定子磁动势一样,即
(21) $n=\frac{60f}{p}$
(22) ${{n}_{\text{s}}}=\frac{60f(1-s)}{p}$
式中,n 为同步转速;f 为基频,p 为极对数,s 为感应电机的转差率,n s 为转子转速。
图10
考虑到气隙磁通密度与转子的非对应关系,UMP随着时间在变化。所以选择一些时间点来分析转子上的UMP。而且,UMP合力的方向与转子弯曲的方向不一致。
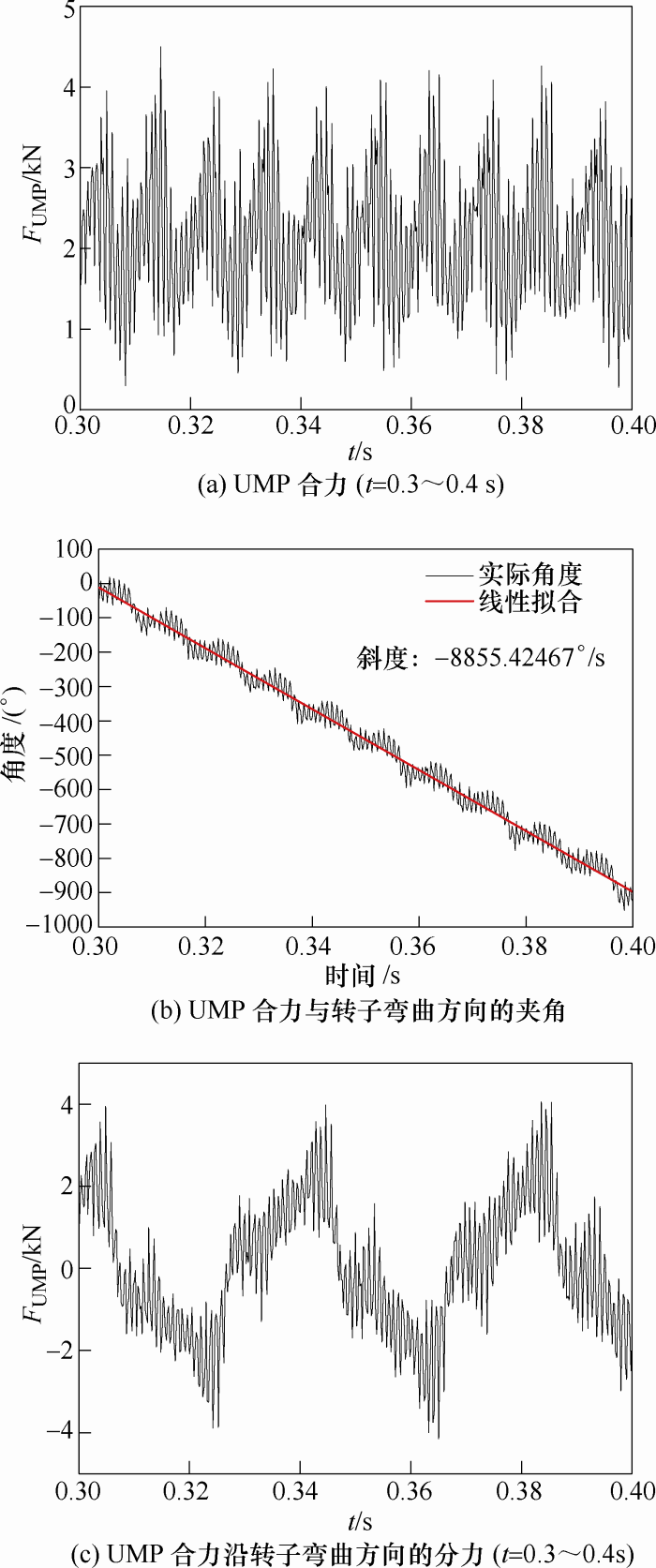
计算得到的UMP合力如图11 a所示。可以看出,UMP合力在△δ max =1%δ 时比较大。UMP合力与转子弯曲方向的夹角如图11 b所示。其夹角在短时间内并不线性但在较长时间里线性度较好。从拟合的斜率来看,其转速与同步速基本一致。也就是说,UMP合力的转速与n -n s 一样。显然,UMP合力的转速远慢于转子转速。UMP合力沿转子弯曲方向的分量如图11 c所示。尽管UMP分量幅值很大,但其平均UMP很小。
图11
图11
UMP合力及其与转子弯曲方向的夹角、沿转子弯曲方向的分力
为了简化计算,将平均UMP分量代入挠曲轴近似微分方程式(5)。平均UMP分量只有19 N,远小于转子自身重力。计算的过程同离心力计算。将UMP分量的挠度加入到表达式$w_{\text{G}}^{\prime }$,则最终表达式为
$w_{\text{G}}^{''}=(-\text{3}\text{.21 }{{z}^{4}}+\text{12}\text{.835}{{z}^{3}}-0.637{{z}^{2}}-$
(23) $\text{24}\text{.44}{{\text{2}}_{{}}}\text{7}z)\times {{10}^{-10}}+{{\varepsilon }^{''}}$
从式(23)可以看出曲线的曲率非常微小,主要挠度是由硅钢片外转子轴的弯曲造成的。
3 扩展对比
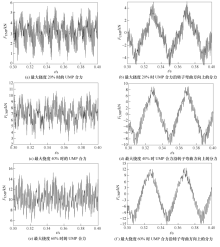
本文对最大挠度为20%、40%以及60%的情况进行了仿真,仿真结果如图12 所示。
图12
图12
不同最大挠度时的UMP合力及其沿转子弯曲方向上的分力
随着偏心度的增加,UMP幅值变大但UMP在等幅上下波动,平均值都很小。也就是说,稳态下的UMP对转子挠度计算不是很重要。
4 结论
本文将弧偏心下的挠度计算分为三个部分。最重要的是第一部分。转子的重力对挠度计算的比重比较大,会引起转子弯曲。然而由重力引起的挠度ε 也不大。偏差主要在于转子的边缘处,这一点可明显从第一部分的计算看出。在第二部分,当挠度很小时,离心力也小。偏心度小于5%的情况下,其影响都可忽略不计。第三部分的计算是UMP的计算。UMP计算相对复杂,它是有关时间的函数。从研究结果看,偏心下平均UMP都很小。通过对比20%、40%、60%的偏心情况,在转子挠度计算中UMP可以被忽略不计。
随着最大挠度变大,挠度曲线的系数变化不大。最大的变化就是最后一项系数。挠度的增加与长时间材料疲劳有关。对于本文这款电机,式(23)可以足够准确模拟任意偏心度时的挠度曲线,并可应用于相关的研究。
参考文献
View Option
[1]
Ebrahimi B M Faiz J Roshtkhari M J . Static-,dynamic-,and mixed-eccentricity fault diagnoses in permanent magnet synchronous motors
[J]. IEEE Transactions on Industrial Electronics , 2009 ,56 (11 ):4727 -4739 .
URL
[本文引用: 1]
[2]
Faiz J Ebrahimi B M Akin B , et al . Finite-element transient analysis of induction motors under mixed eccentricity fault
[J]. IEEE Transactions on Magnetics , 2008 ,44 (1 ):66 -74 .
[本文引用: 1]
[3]
Nandi S Ahmed S Toliyat H A . Detection of rotor slot and other eccentricity related harmonics in a three phase induction motor with different rotor cages
[J]. IEEE Transactions on Energy Conversion , 2001 ,16 (3 ):253 -260 .
URL
[本文引用: 1]
[4]
Nandi S Bharadwaj R M Toliyat H A . Performance analysis of a three-phase induction motor under mixed eccentricity condition
[J]. IEEE Transactions on Energy Conversion , 2002 ,17 (3 ):392 -399 .
URL
[本文引用: 1]
[5]
Hyun D Lee S Hong J , et al . Detection of airgap eccentricity for induction motors using the single-phase rotation test
[J]. IEEE Transactions on Energy Conversion , 2012 ,27 (3 ):689 -696 .
DOI:10.1109/TEC.2012.2198218
URL
Magsci
[本文引用: 1]
The single-phase rotation test (SPRT) is a simple and reliable offline test frequently used for detecting problems in the rotor cage of induction motors without motor disassembly. Airgap eccentricity due to bearing degradation, shaft flexing, etc., is another problem that is difficult to detect, which can cause catastrophic motor failure. In this paper, the feasibility of using the SPRT for detecting eccentricity, which has not been reported before, is investigated. The variation in the inductive component as a function of rotor position and time under static, dynamic, and mixed eccentricity conditions is analyzed. It is shown that airgap eccentricity can be detected in addition to rotor cage problems with the SPRT. An experimental study on a 7.5-Hp induction motor under controlled eccentricity and broken bar conditions shows that airgap eccentricity can be reliably detected with high sensitivity and distinguished from broken rotor bars.
[6]
Dorrell D G Hsieh M Guo Y . Unbalanced magnet pull in large brushless rare-earth permanent magnet motors with rotor eccentricity
[J]. IEEE Transactions on Magnetics , 2009 ,45 (10 ):4586 -4589 .
URL
[本文引用: 1]
[7]
Dorrell D G . Calculation of unbalanced magnetic pull in small cage induction motors with skewed rotors and dynamic rotor eccentricity
[J]. IEEE Transactions on Magnetics , 1996 ,11 (3 ):483 -488 .
URL
[本文引用: 1]
[8]
Dorrell D G . Sources and characteristics of unbalanced magnetic pull in 3-phase cage induction motors with axial-varying rotor eccentricity
[C]. IEEE Energy Conversion Congress and Exposition , 2009 : 240 -247 .
[本文引用: 2]
[9]
Belmans R Vandenput A Geysen W . Calculation of the flux density and the unbalanced magnetic pull in two pole induction machine
[J]. Archiv Fur Elektrotechnik , 1987 ,70 (3 ):151 -161 .
[本文引用: 1]
[10]
Richard P Urban L Mats L . Saturation effects on unbalanced magnetic pull in a hydroelectric generator with an eccentric rotor
[J]. IEEE Transactions on Magnetics , 2007 ,43 (10 ):3884 -3890 .
URL
[本文引用: 1]
[11]
Bradford M . Unbalanced magnetic pull in a 6-pole induction motor
[J]. Proceedings of the Institution of Electrical Engineers , 1968 ,115 (11 ):1619 -1627 .
URL
[本文引用: 1]
[12]
Binns K J Dye M . Identification of principal factors causing unbalanced magnetic pull in cage induction motors
[J]. Proceedings of the Institution of Electrical Engineers , 1973 ,120 (3 ):349 -354 .
[本文引用: 1]
[13]
Arkkio C A Antila M Pokki K , et al . Electromagnetic force on a whirling cage rotor
[J]. IEEE Proceedings- Electric Power Applications , 2000 ,147 (5 ):353 -360 .
URL
[本文引用: 1]
[14]
Di C Bao X Wang H , et al . Modeling and analysis of unbalanced magnetic pull in cage induction motors with curved dynamic eccentricity
[J]. IEEE Transactions on Magnetics , 2015 ,51 (8 ):1 -7 .
URL
[本文引用: 1]
[15]
左曙光 , 林福 , 孙庆 , 等 . 极槽配合和绕组层数对永磁同步电机振动的影响分析
[J]. 振动与冲击 , 2014 ,33 (13 ):130 -134 .
[本文引用: 1]
Zuo Shuguang Lin Fu Sun Qin , et al . Vibration of permanent magnet synchronous motor with different slot-pole combinations and winding layers
[J]. Journal of Vibration and Shock , 2014 ,33 (13 ):130 -134 .
[本文引用: 1]
[16]
代颖 , 崔淑梅 , 张千帆 . 车用异步电机的电磁振动/噪声分析(英文)
[J]. 中国电机工程学报 , 2012 ,32 (33 ):89 -97,180 .
Magsci
[本文引用: 1]
该文对电动汽车驱动用异步电机的电磁振动/噪声进行分析和抑制,以一台额定功率40kW异步电机的电磁噪声分析为例,列写可能引起异步电机电磁振动/噪声的危险电磁力波,并采用有限元法仿真获得电机关键工作点的气隙磁密,对磁密谐波进行时空谐波分析,从而确定危险电磁力波的幅值、次数和频率。采用有限元法分析电机结构的固有频率。通过电磁力波和电机结构的模态分析研究车用异步电机的电磁噪声特性,并通过合理的槽配合选择抑制电磁噪声。测试电机的空载噪声,通过空载噪声频谱的对比证明电磁振动/噪声分析的正确性。
Dai Ying Cui Shumei Zhang Qianfan . Analysis on electromagnetic vibration/noise of induction motors for EV drives
[J]. Proceedings of the CSEE , 2012 ,32 (33 ):89 -97,180 .
Magsci
[本文引用: 1]
该文对电动汽车驱动用异步电机的电磁振动/噪声进行分析和抑制,以一台额定功率40kW异步电机的电磁噪声分析为例,列写可能引起异步电机电磁振动/噪声的危险电磁力波,并采用有限元法仿真获得电机关键工作点的气隙磁密,对磁密谐波进行时空谐波分析,从而确定危险电磁力波的幅值、次数和频率。采用有限元法分析电机结构的固有频率。通过电磁力波和电机结构的模态分析研究车用异步电机的电磁噪声特性,并通过合理的槽配合选择抑制电磁噪声。测试电机的空载噪声,通过空载噪声频谱的对比证明电磁振动/噪声分析的正确性。
[17]
马琮淦 , 左曙光 , 孙庆 , 等 . 考虑时间谐波电流的永磁同步电机电磁噪声阶次特征分析
[J]. 振动与冲击 , 2014 ,33 (15 ):108 -113,125 .
[本文引用: 1]
Ma Conggan Zuo Shuguang Sun Qing , et al . Order feature analysis of electromagnetic noise in a permanent magnet synchronous motor considering current harmonics
[J]. Journal of Vibration and Shock , 2014 ,33 (15 ):108 -113,125 .
[本文引用: 1]
[18]
诸自强 , 刘旭 , 潘再平 . 新型可变磁通磁阻电机振动和噪声研究与开关磁阻电机的比较(英文)
[J]. 电工技术学报 , 2013 ,28 (11 ):9 -18 .
[本文引用: 1]
Zhu Ziqiang Liu Xu Pan Zaiping . Investigation of vibration and noise in novel variable flux reluctance machine with reference to switched reluctance machine
[J]. Transactions of China Electrotechnical Society , 2013 ,28 (11 ):9 -18 .
[本文引用: 1]
[19]
He G Huang Z Qin R , et al . Numerical prediction of electromagnetic vibration and noise of permanent magnet direct current commutator motors with rotor eccentricities and glue effects
[J]. IEEE Transactions on Magnetics , 2012 ,48 (5 ):1924 -1931 .
DOI:10.1109/TMAG.2011.2178100
Magsci
[本文引用: 1]
Numerical models are developed to predict the electromagnetic vibration and noise of permanent-magnet direct current (PMDC) commutator motors when both rotor eccentricities and glue effects are involved. Finite-element method (FEM) and boundary-element method (BEM) are combined to analyze the electromagnetic, mechanical, and acoustical characteristics of the studied motor. By using the finite-element method, an electromagnetic field considered as the electromagnetic vibration and noise sources of the motor is calculated in the two-dimensional air-gap region. Based on the electromagnetic field, the radial and tangential magnetic forces exciting the structure of the motor are then obtained in the time and frequency domains. Consequently, the transient responses (accelerations) of the motor are simulated by applying the magnetic forces on the three-dimensional dynamic-structure finite-element model of the motor. Furthermore, the sound pressures radiated from the vibrating surface of the motor can be obtained by using the boundary-element method in the frequency domain. The numerical results agree well with those measured in the laboratory. The present research reveals that the static eccentricity distorts the distribution of the magnetic forces in the spatial domain. And the distorted magnetic forces mainly exaggerate the accelerations of the motor for the frequency range which is lower than the natural frequencies of the motor. In addition, the epoxide-resin glue between the permanent magnets and the stator can influence the vibrational and the acoustical characteristics of the motor.
[20]
Jia S Qu R Li J et al . Analysis of FSCW SPM servo motor with static,dynamic and mixed eccentricity in aspects of radial force and vibration
[C]. IEEE Energy Conversion Congress and Exposition (ECCE),Pittsburgh,PA , 2014 : 1745 -1753 .
[本文引用: 1]
[21]
Kim D Kim H Hong J , et al . Estimation of acoustic noise and vibration in an induction machine considering rotor eccentricity
[J]. IEEE Transactions on Magnetics , 2014 ,50 (2 ):857 -860 .
URL
[本文引用: 1]
Static-,dynamic-,and mixed-eccentricity fault diagnoses in permanent magnet synchronous motors
1
2009
... 偏心的相关研究主要包括内部和外部. 偏心的外部分析对象是定子电流信号、转矩信号等.许多文献对偏心问题进行了研究.文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎.快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具.希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点.偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题. ...
Finite-element transient analysis of induction motors under mixed eccentricity fault
1
2008
... 偏心的相关研究主要包括内部和外部. 偏心的外部分析对象是定子电流信号、转矩信号等.许多文献对偏心问题进行了研究.文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎.快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具.希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点.偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题. ...
Detection of rotor slot and other eccentricity related harmonics in a three phase induction motor with different rotor cages
1
2001
... 偏心的相关研究主要包括内部和外部. 偏心的外部分析对象是定子电流信号、转矩信号等.许多文献对偏心问题进行了研究.文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎.快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具.希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点.偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题. ...
Performance analysis of a three-phase induction motor under mixed eccentricity condition
1
2002
... 偏心的相关研究主要包括内部和外部. 偏心的外部分析对象是定子电流信号、转矩信号等.许多文献对偏心问题进行了研究.文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎.快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具.希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点.偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题. ...
Detection of airgap eccentricity for induction motors using the single-phase rotation test
1
2012
... 偏心的相关研究主要包括内部和外部. 偏心的外部分析对象是定子电流信号、转矩信号等.许多文献对偏心问题进行了研究.文献[1 ,2 ]对永磁同步电动机的静态、动态以及混合偏心的故障诊断做了研究;文献[3 ,4 ,5 ]在偏心故障检测领域也有所涉猎.快速傅里叶变换和小波变换已成为偏心故障检测中常用的分析工具.希尔伯特-黄变换是一种新的分析工具,正逐渐成为检测领域的热点.偏心的内部分析指的是由不均匀的气隙所引起的气隙磁通密度变化、不平衡磁拉力(Unbalanced Magnetic Pull,UMP)等问题. ...
Unbalanced magnet pull in large brushless rare-earth permanent magnet motors with rotor eccentricity
1
2009
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Calculation of unbalanced magnetic pull in small cage induction motors with skewed rotors and dynamic rotor eccentricity
1
1996
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Sources and characteristics of unbalanced magnetic pull in 3-phase cage induction motors with axial-varying rotor eccentricity
2
2009
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
... [8 ]. ...
Calculation of the flux density and the unbalanced magnetic pull in two pole induction machine
1
1987
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Saturation effects on unbalanced magnetic pull in a hydroelectric generator with an eccentric rotor
1
2007
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Unbalanced magnetic pull in a 6-pole induction motor
1
1968
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Identification of principal factors causing unbalanced magnetic pull in cage induction motors
1
1973
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Electromagnetic force on a whirling cage rotor
1
2000
... 文献[6 ,7 ]在不平衡磁拉力问题上做了很多研究工作;并在文献[8 ]中详细地总结了不平衡磁拉力的研究结果.最近的研究,如文献[9 ,10 ],考虑了涡流效应以及负载因素,使用傅里叶级数分析得出不平衡磁拉力的解析表达式.不平衡磁拉力一直以来都是一个重要的研究问题,此外,文献[11 ,12 ,13 ]也致力于这方面的研究.然而,由于感应电机有两个相对独立的电路环,其中转子电路需要另外计算,相较于其他类型(有永磁体)的电机,感应电机的不平衡磁拉力问题变得更加复杂.另外,笼型转子中的平行电路也应当加入到计算中,这种并联电路对于UMP是一种阻尼.定子绕组设置成多并联支路数也会限制UMP的大小[8 ] . ...
Modeling and analysis of unbalanced magnetic pull in cage induction motors with curved dynamic eccentricity
1
2015
... 虽然有关偏心研究的文献有很多,但有关弧偏心(实际)[14 ] 的研究却很少.本文进行了弧偏心的基础研究,首次从力学角度研究弧偏心的整个过程,详细分析产生弧形挠度的主要原因.主要内容分三部分:首先是重力部分.如果没有重力并且材料的弹性模量属性不存在,离心力和不平衡磁拉力也就不需要讨论了;第二部分是离心力部分.当存在挠度时,离心力就会一直存在;第三部分是不平衡磁拉力.当电机转子出现较大挠度时,转子所受的不平衡磁拉力会很大.另外,根据研究,不平衡磁拉力是一个有关时间的函数. ...
极槽配合和绕组层数对永磁同步电机振动的影响分析
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
极槽配合和绕组层数对永磁同步电机振动的影响分析
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
车用异步电机的电磁振动/噪声分析(英文)
1
2012
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
车用异步电机的电磁振动/噪声分析(英文)
1
2012
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
考虑时间谐波电流的永磁同步电机电磁噪声阶次特征分析
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
考虑时间谐波电流的永磁同步电机电磁噪声阶次特征分析
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
新型可变磁通磁阻电机振动和噪声研究与开关磁阻电机的比较(英文)
1
2013
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
新型可变磁通磁阻电机振动和噪声研究与开关磁阻电机的比较(英文)
1
2013
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
Numerical prediction of electromagnetic vibration and noise of permanent magnet direct current commutator motors with rotor eccentricities and glue effects
1
2012
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
Analysis of FSCW SPM servo motor with static,dynamic and mixed eccentricity in aspects of radial force and vibration
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...
Estimation of acoustic noise and vibration in an induction machine considering rotor eccentricity
1
2014
... 过大的偏心值会产生很大的不平衡磁拉力,一方面增加轴承的机械磨损,削弱轴承的使用寿命;另一方面,在定子齿部产生一些高次力波,改变了电机结构的固有频率,增加了噪声.电机的振动与噪声研究一直以来是比较热门的方向.文献[15 ]研究了极槽配合和绕组层数对永磁同步电机振动的影响,对不同状态下的最低阶径向力波幅值进行了比较.文献[16 ]通过有限元方法对一台车用40 kW异步电机进行电磁力波和电机结构的模态分析,得出需要避让的固有频率,并研究了不同极槽配合下的电磁噪声.文献[17 ]通过噪声测试试验发现除了偶数阶、开关频率附近阶次的主要谐波,还有以往研究中忽略的分数阶次谐波.应用复合科特斯公式对径向力波积分,求得具有六阶代数精度的径向集中力,建立了一种考虑时间谐波电流的电机电磁噪声数学预测模型.文献[18 ]通过电磁场、力学场及声学场有限元方法计算并试验研究了一种可变磁通磁阻电机的振动噪声.文献[19 ]建立了数值模型预测偏心下带换向器的永磁直流电机的电磁振动和噪声.文献[20 ]通过解析法和有限元法分析研究静态偏心、动态偏心以及混合偏心对表贴式永磁电机的性能影响,研究表明静态偏心只改变径向力的模态阶数而动态偏心和混合偏心增加振动频率和模态阶数,这就使得偏心电机的振动频率更接近于其自然频率,力波模态和电机模态相近,当达到一定程度,偏心电机会产生巨大的振动与噪声.文献[21 ]通过有限元法和试验研究了一台3.7 kW的异步电机静态偏心下的电磁激振力和振动噪声,发现静态偏心使得噪声的基次和31次谐波成分随着偏心度有所增加. ...