1 引言
世界一次能源结构在缓慢发生变化,根据IEA预测,截止2030年世界一次能源消耗结构中,煤炭、石油、天然气、水能、核能、生物质及废弃物以及其他可再生能源分别占总消费结构的28.8%、30%、21.6%、2.4%、5.3%、9.8%和2.1%[1]。在IEA预测的2030年主要国家的用电需求中,我国的用电需求量稳居第一,而一次能源消费结构变化中可再生能源占比也由2006年的0.6%增加到2030年的2.1%。
目前可再生能源中光伏发电和燃料电池发电成为了主流。然而光伏和燃料电池的输出电压范围宽、电压低、输出电流纹波大,无法直接作为并网逆变的输入电压,一般来说燃料电池输出电压为36~60 V,并网逆变输入电压等级却在200~600 V,因此需要一种直流升压变换器来满足新能源发电需求[2]。
传统Boost变换器理论上能够实现全占空比范围升压,但是电压增益低、开关器件电压应力大,不适用于新能源逆变并网发电系统,所以研究新型高增益直流升压变换器意义重大。
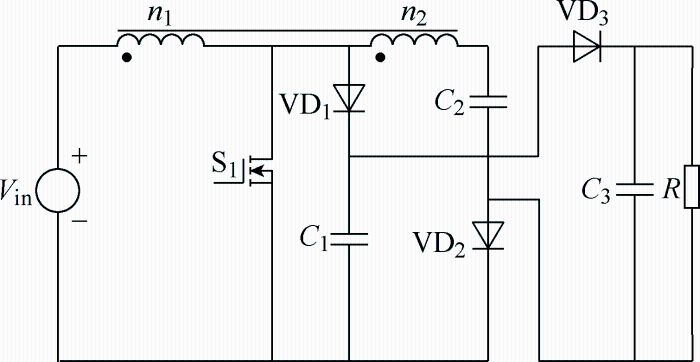
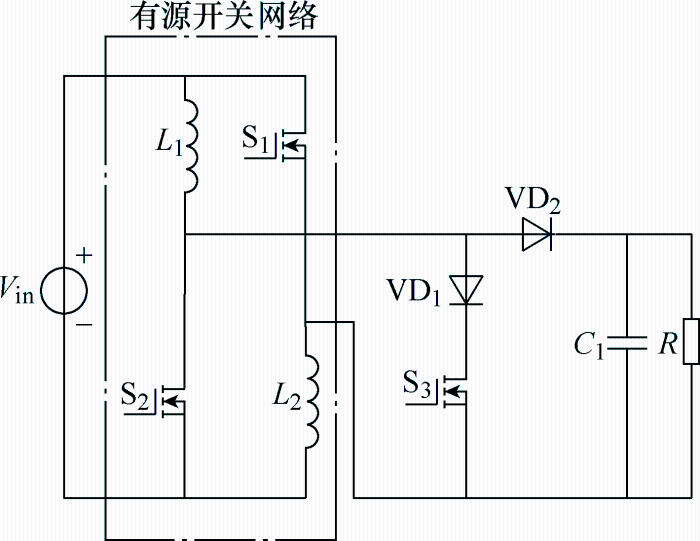
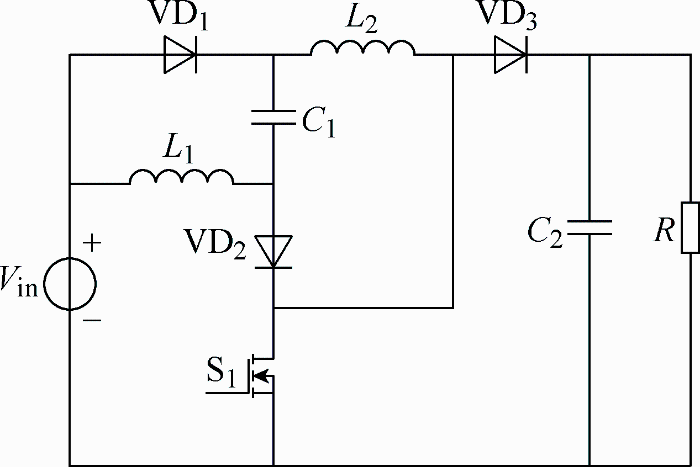
文献[3]在电容桥式倍压单元中加入耦合电感,得到了结构简单、增益较高的非隔离直流变换器,拓扑结构如图1所示,但是耦合电感漏感易导致较高的开关管电压尖峰,造成整机效率降低;文献[4]将传统Boost变换器输入电感用有源开关网络替代,得到了一种高增益DC-DC变换器,拓扑结构如图2所示,该变换器不仅结构简单,而且使用了较少的无源器件,使得变换器转换效率提高,但是电路增益效果仍不明显,开关器件电压应力高,增加了开关器件导通损耗,且不适用于高压输出场合;文献[5]在传统Boost变换器基础上利用电感电容并联充电、串联放电的特点,得到了一种单管双电感高增益直流变换器,拓扑结构如图3所示,该变换器将电压增益提高为传统Boost变换器的两倍,电路转换效率高,但是开关器件电压应力仍然为输出电压。
图1
图2
图3
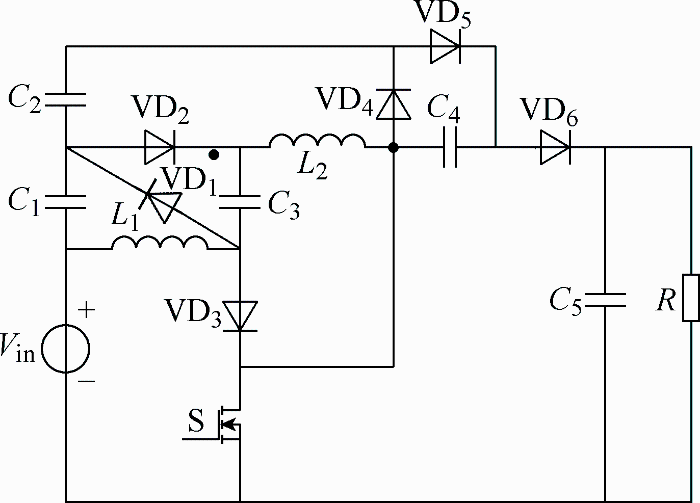
本文为了解决上述高增益变换器存在的缺点,在文献[5]所提变换器中加入自举升压单元,提出一种单开关非隔离新型高变换比DC-DC变换器。该变换器具有高增益、低开关应力、高效率的特点,特别适用于新能源发电系统。详细分析了本文所提变换器的工作原理和稳态特性,最后通过仿真实验验证了理论分析的正确性。
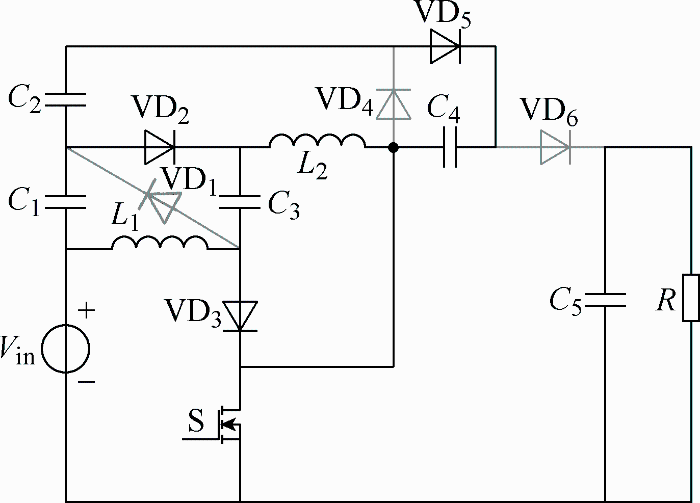
2 变换器拓扑结构与工作原理
2.1 变换器拓扑
单管双电感高增益DC-DC变换器拓扑结构见图3,变换器工作过程可描述为:开关管S1开通时,电感L1、L2和电容C1并联充电;开关管关断时,电感L1、L2和电容C1串联放电,提高了电路增益,此时增益M的表达式为
式中,Vo为输出电压;Vin为输入电压;D为开关占空比。
图4
2.2 变换器工作原理
为了简述电路工作过程,假设电路工作于电感电流连续模式,且开关器件导通压降均为零,电容可以看作恒压源。开关周期设为Ts,占空比为D,不考虑开关管寄生参数时电路主要有两种工作模态。
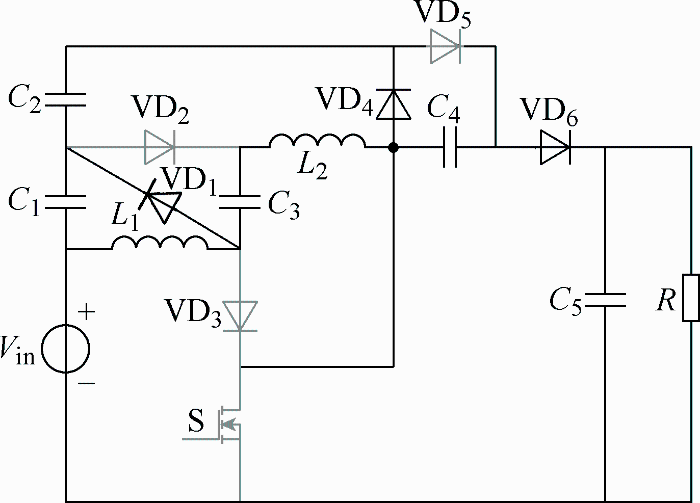
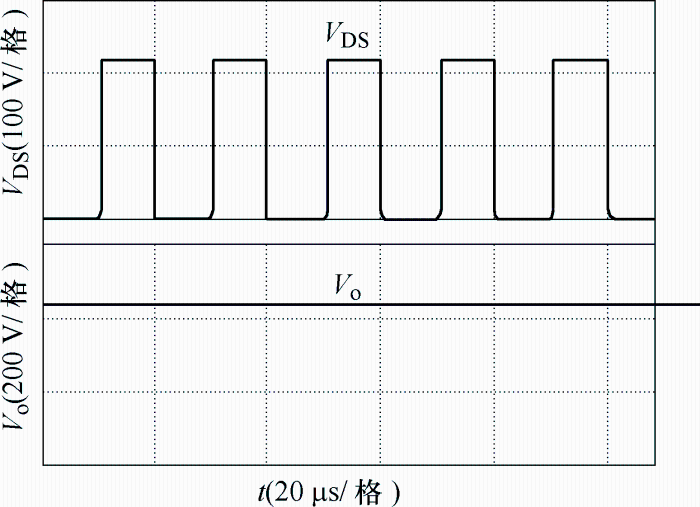
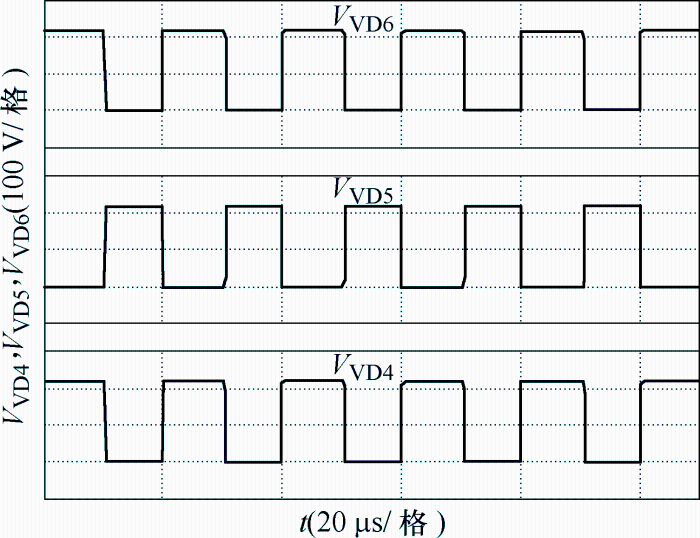
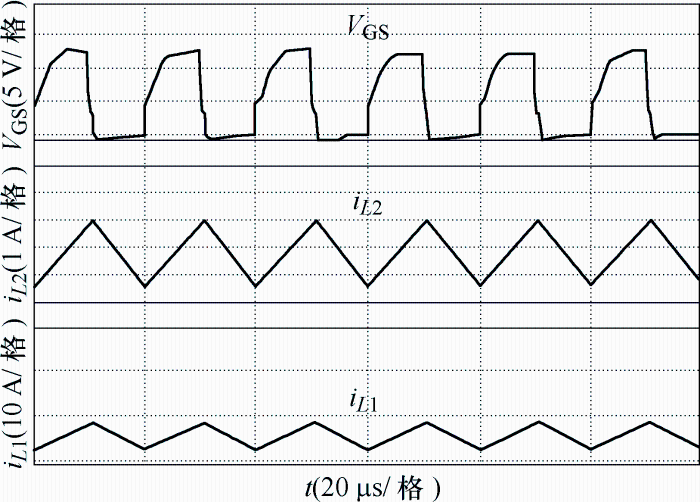
(1) 模态1[t1~t2]。此模态下开关S导通,VD2、VD3和VD5二极管正向导通,VD1、VD4和VD6二极管截止,L1与输入源Vin并联,L1电流iL1线性上升。C1与Vin串联,共同为C3和L2充电,C3两端电压线性上升,L2电流线性上升。C4由C1、C2和Vin三者串联充电,同时C5给负载R供电。模态1工作电路如图5所示。
图5
iL1和iL2可用数学方程表示为
式中,IL1(t1)为L1在t1时刻的电流;IL2为L2在t2时刻的电流;VC1为电容C1的稳态电压。
(2) 模态2[t2~t3]。此模态下开关S关断,各开关器件开关状态发生翻转,L1、L2电感电压极性翻转,Vin、L1、L2、C2和C4电压串联,与输出电压Vo相等,由于开关管与输出电压之间有电容C4,所以开关电压应力有所降低。S关断期间,L1给C1充电、L2给C2充电,以补充C1和C2在模态1阶段释放的能量。此阶段模态图如图6所示。
图6
iL1和iL2可用数学方程表示为
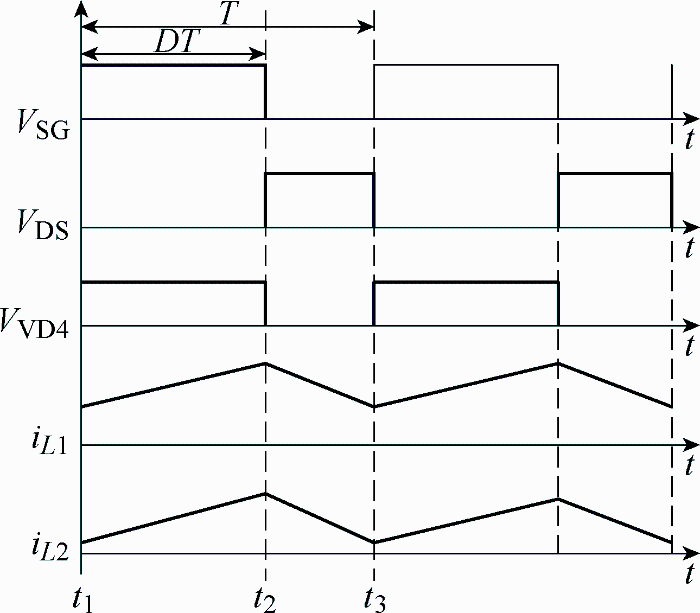
根据上述两种工作模态可得出电路的主要工作波形,如图7所示。
图7
3 稳态性能分析
3.1 电压传输比
根据模态1和模态2,可列出稳态方程,即
模态1
模态2
联立式(6)、(7)以及图7中电感电流一周期内伏秒积平衡,可解得电路的稳态增益M为
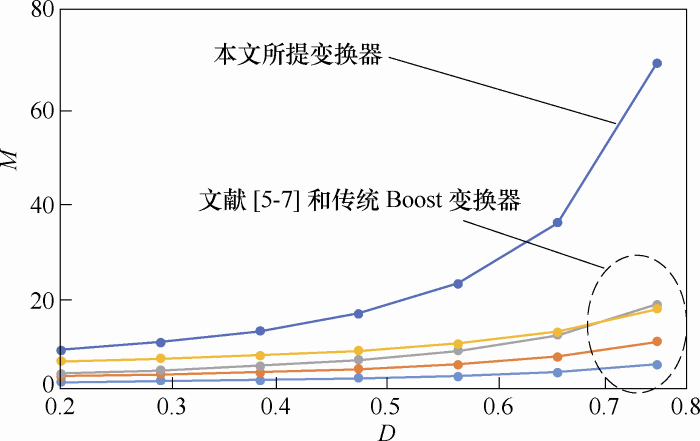
图8
从图8可以看出,本文所提变换器增益较高,使得变换器不必在极限占空比时实现高增益。
3.2 开关器件电压应力分析
当开关管关断时,开关器件所承受的电压应力为
式中,VDS为开关管漏源电压;VVD1~VVD6为二极管VD1~VD6的反向电压。
从式(9)可以看出,变换器的电压应力相比于传统Boost变换器和文献[5]所提变换器开关电压应力而言有所降低。
3.3 电感电流纹波分析
电感电流纹波与电感两端电压、开关占空比以及开关频率有关,根据式(6)可写出电感电流的纹波方程,即
式中,ΔiL1为电感L1的电流纹波;ΔiL2为电感L2的电流纹波;f为开关频率。
4 仿真结果分析
为了验证理论分析的正确性,本文在Saber仿真环境中搭建了200 W仿真模型。Saber仿真平台可以选取具体开关器件型号进行物理层面的仿真,仿真参数及型号见下表。
表 200 W仿真试验参数及型号
| 物理量 | 参数值 | 型号/条件 |
|---|---|---|
| 输入电压Vin/V | 36 | |
| 开关占空比D | 0.4 | |
| 开关频率f/kHz | 50 | |
| 开关管S | 55 A/500 V | IXFK55N50 |
| 二极管VD1~VD6 | 16 A/600 V | MUR1660 |
| 电容C1/μF | 68 | 50 V |
| 电容C2/μF | 100 | 150 V |
| 电容C3/μF | 86 | 100 V |
| 电容C4/μF | 150 | 200 V |
| 电容C5/μF | 470 | 600 V |
| L1/μH | 60 | 7 A |
| L2/μH | 300 | 10 A |
| 电阻R/kΩ | 1 | 0.25 W |
图9
图10
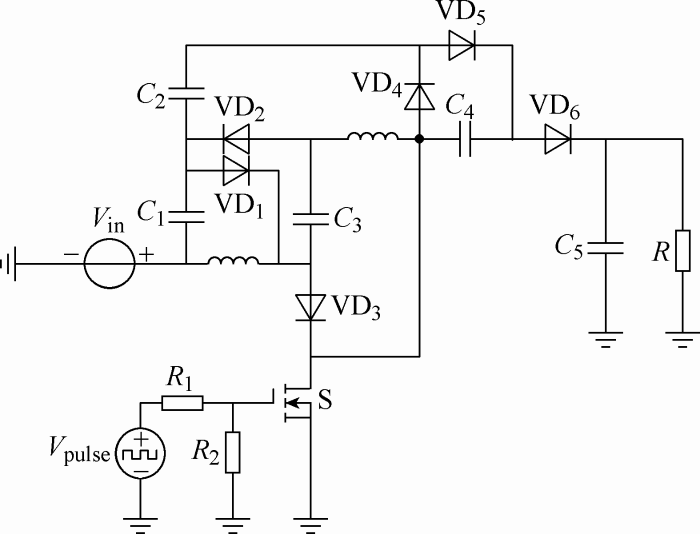
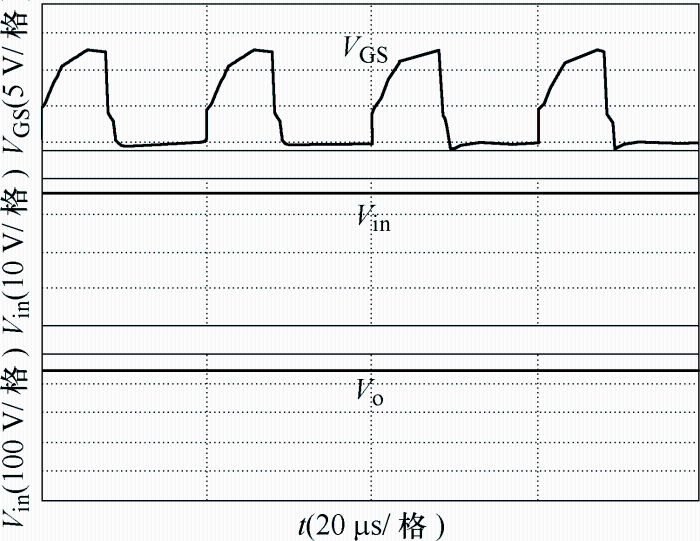
输入电压Vin和输出电压Vo的波形,可以看出,当输入Vin=36 V,输出电压Vo=438.1 V,此时占空比D=0.4,与式(8)理论计算值440 V相符。
图11
图12
图13
图14
5 结论
为了解决传统Boost变换器低增益、高电压应力的问题,本文以文献[5]电路模型为基础,加入自举升压电容,提出了一种新型高升压比DC-DC变换器拓扑,研究了变换器的稳态特性,推导出变换器中的电感电流纹波,并通过Saber进行了仿真验证,得到如下结论。
(1) 电路结构简单,有利于提高电路效率。
(2) 变换器具有高增益、低开关电压应力、电流连续的特点,有利于延长燃料电池的使用寿命。
参考文献
2030年世界与电力发展展望
[J].
World energy and electricity outlook for 2030
[J].
基于开关电容的高增益双输入Boost变换器
[J].
The double-input Boost converter with high-gain based on switched-capacitor
[J].
Analysis and implementation of high-gain non-isolated DC-DC boost converter
[J].
Non-isolated high gain DC-DC converter for DC microgrids
[J].
一种单管双电感高增益Boost变换器
[J].
Single switch high step-up converter with double-inductor
[J].
一种新型开关电感、开关电容的高增益Boost变换器
[J].
A new high-gain Boost converter based on switched inductor/capacitance
[J].