电气工程学报, 2019, 14(2): 1-6 doi: 10.11985/2019.02.001

轴电流问题中轴承模型的探究及等效电阻计算 *

任雪娇, 刘瑞芳,, 王芹芹

北京交通大学电气工程学院 北京 100044

Research on Bearing Model of Bearing Current Analysis and Calculation of Equivalent Resistance

REN Xuejiao, LIU Ruifang,, WANG Qinqin

School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044 China

通讯作者: 刘瑞芳，女，1971年生，副教授，博士研究生导师。研究方向为电力电子与电机系统集成分析、电磁场数值计算。E-mail：rfliu@bjtu.edu.cn

收稿日期: 2019-05-10   网络出版日期: 2019-06-25

基金资助: *国家自然科学基金资助项目.  51777008

Received: 2019-05-10   Online: 2019-06-25

作者简介 About authors

任雪娇,女,1993年生,硕士研究生。研究方向为电磁场理论及数值计算。E-mail：16121509@bjtu.edu.cn

摘要

随着PWM变频调控技术在电机驱动中的广泛应用,轴电流问题越来越突出。在分析和预测轴电流时最为复杂的问题之一是轴承等效电气模型的建立,以往模型中将轴承等效为简单的电容和电阻串、并联的组合,但由该模型得到的轴承击穿波形与实际测得的击穿波形并不相符。从轴承击穿电压、电流波形出发,结合轴承实际结构,提出一种改进的轴承等效模型。该模型中轴承等效击穿电阻为可变电阻,并结合电弧击穿理论确定了可变电阻的计算方法。对基于新模型的轴承等效电路进行仿真,并与试验测得的击穿波形图对比。结果表明,与恒定电阻模型相比,提出的模型能更好地模拟轴承击穿和恢复的过渡过程。

关键词： 轴电流 ; 轴承模型 ; 击穿电阻 ; 电弧理论

Abstract

：With the wide application of pulse width modulation (PWM) technology in motor drive, the bearing current problem becomes more and more prominent. The bearing equivalent model is one of the most complicated problems in analyzing bearing currents. Usually a simple capacitor, resistor series or parallel circuit is used to model the bearing breakdown process, but it is not consistent with the experiment result. An improved equivalent bearing model is proposed, which is derived from the structure of the bearing and the waveform of the bearing breakdown. The equivalent breakdown resistance of the bearing is variable, which is determined through the arc breakdown theory. Comparing the simulation waveforms with the experiment waveforms, the proposed equivalent bearing model is more accurate than the previous constant resistant model.

Keywords： Bearing current ; bearing model ; breakdown resistance ; arc theory

PDF (757KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

任雪娇, 刘瑞芳, 王芹芹. 轴电流问题中轴承模型的探究及等效电阻计算 *. 电气工程学报[J], 2019, 14(2): 1-6 doi:10.11985/2019.02.001

REN Xuejiao. Research on Bearing Model of Bearing Current Analysis and Calculation of Equivalent Resistance. Journal of Electrical Engineering[J], 2019, 14(2): 1-6 doi:10.11985/2019.02.001

1 引言

目前,PWM变频驱动技术在电机控制系统中的应用越来越广泛,然而,由此带来的轴承电腐蚀问题也引起了工业界和学术界的关注[1,2,3]。变频器输出的共模电压会施加在电机绕组和地之间,而电机内部存在寄生电容,共模电压在电容耦合作用下,电机轴承内外圈会感应出高频轴电压。轴电压超过轴承电容的阈值电压时,轴承的润滑油膜会发生击穿放电,产生的短路电流会在很短的时间产生巨大的热量,这些热量足以融化击穿点附近的金属,从而形成坑点。一旦轴承受到电腐蚀而产生蚀点、凹槽,电机运行时的振动和噪声就会增加,直接影响了电机运行的可靠性,如果轴承腐蚀进一步恶化,引起电机故障,会造成经济损失,甚至导致人员伤亡。因此,对轴电流的分析和抑制具有重要的工程意义。

在轴电流的产生机理[4]、电机内部杂散电容参数的计算[5,6]以及轴电流的等效电路结构的分析[7,8,9]等方面已经有许多研究成果。但是,在轴电流问题中最复杂、最难模拟的是轴承部件。轴承未被击穿时,内外滚道、滚珠和润滑油形成了电容。电容的大小与载荷、转速、温度等有密切的关系,文献[10,11]利用赫兹接触面积计算了轴承电容的等效值;文献[12]根据轴承的实际结构,通过不同位置处滚珠润滑油膜的中心厚度来计算各部分的电容,然后将各部分的电容相加得到轴承的等效电容。轴承击穿后,呈现电阻状态;文献[13]将轴承等效为简单的电容、电阻串联结构;文献[14]将轴承等效为电容和电阻并联。然而,从试验测取的轴承击穿的波形图来看,从电容态到电阻态和电阻态到电容态都是有逐渐变化的趋势的。此时用简单的轴承等效电容与恒定值电阻的串、并联不足以反映这一现象。所以,本文将从轴承击穿波形出发,结合轴承实际结构以及击穿机理,提出一种新的轴承等效电路模型,并结合电弧理论确定击穿等效电阻。将新模型和以往模型的仿真与试验结果进行对比,分析新模型的准确性。

2 轴承电气等效模型

搭建准确的轴承电气等效模型是预测轴电流的关键环节。因为轴承击穿过程涉及摩擦学、热力学等交叉学科的知识,所以对轴承部件的准确模拟是一个难题。下面从轴承结构出发对轴承等效电路进行分析。

2.1 轴承结构

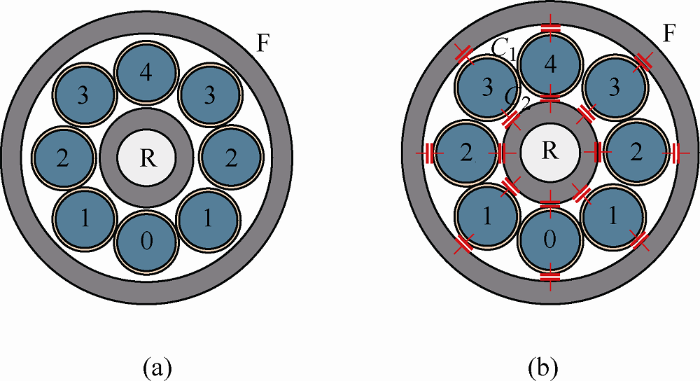
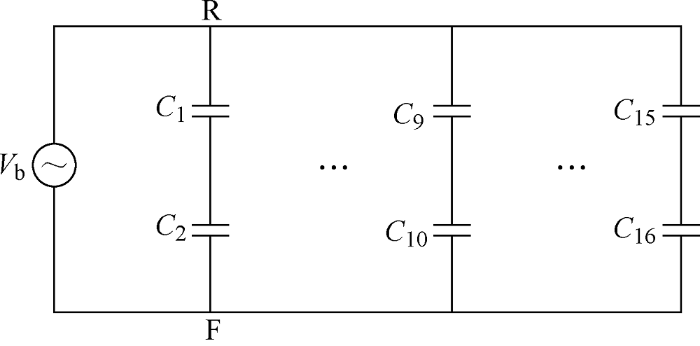
滚动轴承应用广泛、结构简单,电机中滚动轴承主要起支撑和传动的作用,保证电机定、转子之间保持一定气隙的同时确保负荷的有效传递。滚动轴承一般由内滚道、外滚道、滚动体、保持架、润滑油脂等组成。中小型电机中常采用的深沟球轴承如图1a所示。轴承内滚道与转轴(R)相连,外滚道与电机机壳(F)相连,内外滚道之间为滚珠。润滑油脂将轴承的滚珠和内、外滚道隔开,在电机稳定运行时形成一层绝缘润滑油膜,润滑油膜一方面起到润滑作用,减小零件之间的机械摩擦从而提高传动效率,另一方面将滚动体包裹,起到隔绝保护的作用。从电路角度来看,润滑油膜的绝缘特性使滚珠和滚道之间构成了电容,以3号滚珠为例,滚珠和内滚道间存在电容C1、滚珠与外滚道间存在电容C2,润滑油膜充当绝缘介质,8个滚珠就有电容C1~C16,如图1b所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   轴承结构简图


对图1b中的轴承电容分布图沿半径切开,再沿周长展开后得轴承电容等效电路,如图2所示。图2中,每两个电容串联,代表同一个滚珠分别与内、外滚道形成的两个电容;N个滚珠则有N条双电容支路并联。Vb为轴电压,由变频器的共模电压在转轴和机壳之间感应产生。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   轴承电容等效电路


当轴承润滑油膜两侧的电压超过油膜能承受的阈值电压时,油膜被击穿。对外表现的特征为轴电压突然降低、轴电流突然增加,击穿后呈现电阻状态。因此,为了模拟击穿的状态,在每个电容上并联一个电阻,得到轴承等效电容电阻电路,如图3所示。在电容和电阻支路上都设有开关,未击穿时电容电路接通,电阻电路断开;击穿后则相反。由图3可知,只有当同一条支路的两个电容同时被击穿时才会出现较大的击穿电流,这意味着一个滚珠两侧的油膜同时被击穿时才会出现击穿电流。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   轴承电容电阻等效电路


2.2 轴承电路模型的简化

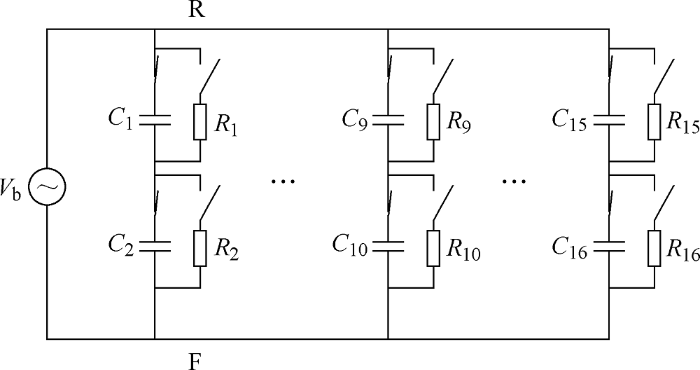
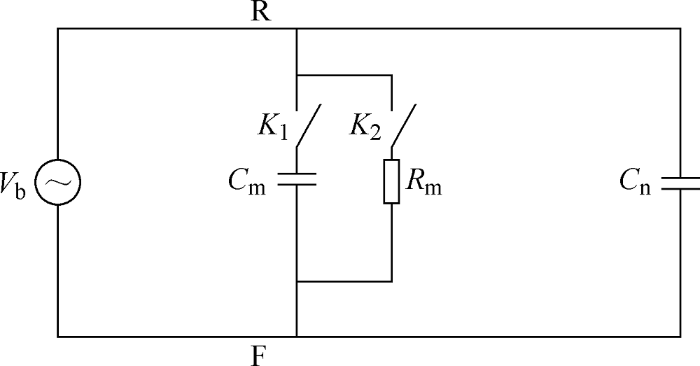
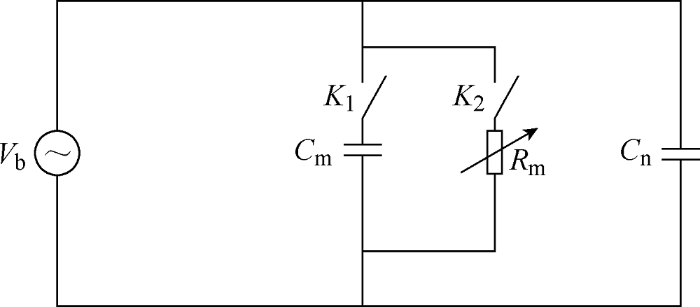
对于不同位置的滚珠,即使在高速运行中的轴承,也有不同的情况。图1中,将8个滚珠分为4种不同的位置,它们受载荷的影响与内、外滚道形成的电容是不同的[12]。但是,如果载荷、转速等外部条件一定,在任何时刻滚珠都会呈现如图1所示的分布,也就是说在电路中总会有轴承电容C1~C16,而且这些电容的相互关系不变,即轴承的内部等效电路不变。运行中的轴承也可以用图3静态电路来模拟。

首先,为了方便分析,可以对电路进行简化。因为击穿的发生是随机的,所以假设击穿只发生在某一个滚珠上,而且此处所说的击穿指的是同一个滚珠与内、外滚道形成的两个电容同时被击穿,即电路中同一条支路上的两个电容同时被击穿。将被击穿电容所在的支路另外列出,剩下的几条并联电容合并,同时将各条支路上串联的电容合并,可得到轴承的简化模型,如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   轴承的简化模型


图4中,Cm为被击穿处滚珠与内、外滚道形成的电容之和;Cn为未被击穿的滚珠与内、外滚道形成的等效电容;Rm为电容被Cm击穿后的等效电阻;K1、K 2为电容支路和电阻支路的开关。

2.3 改进的轴承模型

据文献[5],轴承发生轴电流击穿时,轴电压下降、轴电流升高,而且击穿后轴电压、轴电流的包络线不是阶跃式转化,而是随时间逐渐变化,因此在图4中用恒定电阻模拟击穿后的状态并不准确。针对这一问题,本文提出一种改进的轴承等效模型,如图5所示,图中击穿时等效电阻Rm为一个可变电阻。这是不同于以往文献中的轴承等效模型。图5中,Cm、Cn、Rm的确定是问题的关键。下面将结合6208型深沟球轴承以及轴电流测试结果讨论轴承等效电气参数的确定方法。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   轴承的改进模型


3 轴承等效模型中电气参数的确定

3.1 轴承模型中电容参数的确定

轴承电容的计算方法有很多种[5, 15-16],文献[5]给出了改进后的轴承等效电容计算方法：先计算中心油膜厚度,以此作为滚珠与内、外极板形成的电容极板的最小距离,两极板面的其他区域的实际距离根据几何关系得出。然后采用三维有限元计算得出各滚珠的轴承等效电容。该文献针对6028型轴承进行分析,得到各位置处的电容值,其中,Ci为滚珠与内滚道之间的电容;Co为滚珠与外滚道之间的电容。将同一滚珠位置处的Ci与Co串联,可得到各位置下的电容Cbi,上述结果见下表,其中i为滚珠位置,Ci与Co的计算结果见文献[5]。

表   轴承各滚珠对应电容计算结果

i01234
Co/pF23.623.322.922.320.6
Ci/pF10.910.09.47.75.6
Cbi/pF7.457.006.665.724.40

新窗口打开| 下载CSV


电容越大,油膜厚度越薄。当外加电压相同时,油膜越薄,越容易击穿。所以分析上表中数据可以得出结论：位置0处即轴承正下方的滚珠更容易发生击穿。另外,考虑轴两端各有一个轴承,所以对应图5中电容参数为

${{C}_{\text{m}}}=2{{C}_{\text{b0}}}$
${{C}_{\text{n}}}=2(2{{C}_{\text{b1}}}+2{{C}_{\text{b2}}}+2{{C}_{\text{b3}}}+{{C}_{\text{b4}}})$

3.2 可变击穿电阻的确定

电火花放电从放电形态的角度分为火花放电、过度放电和电弧放电[17]。轴承击穿属于火花放电,火花放电的特点是每个脉冲的等离子体放电通道都必须是重新击穿加工介质而形成;电弧放电的介质是气体,是一种持续放电的现象。但两种放电有很多相似之处,火花放电和电弧放电都是介质中粒子发生碰撞电离形成的。电弧模型可分为三个阶段[18]：起弧、稳定和熄弧。观测轴承击穿过程轴电压和轴电流波形也可以分为三个阶段[5] ：电容向电阻过渡(电压下降、电流上升)阶段、稳定阶段和电阻恢复为电容(电压上升、电流下降)阶段。由于两种放电的对外特征相似,本文采用电弧等效电阻的计算方法来确定轴承击穿电阻。

与轴承击穿过程对应,轴承击穿电阻也可以分为三个阶段：起始阶段电阻Rm1、稳定阶段电阻R0和恢复阶段电阻Rm2。根据文献[18]电弧放电的电阻模型给出Rm1和Rm2的表达式为

${{R}_{\text{m1}}}={{r}_{0}}+r\text{exp}\left( -\frac{t}{{{\tau }_{1}}} \right)$
${{R}_{\text{m2}}}\approx {{R}_{0}}\text{exp}\left( \frac{t}{{{\tau }_{2}}} \right)$

式中,r0为静态点电阻,通常取0.5 Ω;r为轴承未击穿时的阻值;τ1为击穿形成时的时间常数,τ1=rCm;τ2为油膜恢复的时间常数,τ2=R0Cm。模型中待定量为轴承未击穿时阻值r和稳定阶段电阻R0,这两个参数可以通过试验测量获取。

4 可变电阻参数的确定方法

4.1 试验装置

给一台Y2-135S型5.5 kW三相感应电机的定子绕组施加三相交流电,驱动电机旋转。在电机一侧的转轴和机壳之间施加高频脉冲信号,该信号施加在轴承内外滚道之间。通过测量对侧轴承的轴电流、轴电压可以获得轴承的伏安特性,试验装置如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   试验装置


为了实现轴电流的测量,对电机进行改造,在轴承外圈和轴承座之间加了一层绝缘,通过一个铜导线将轴承外圈和轴承座进行电气连接[5]。高频电压激励通过函数信号发生器输出。Suin TFG6930A型函数信号发生器内阻为50 Ω,可输出±20 V、0~30 MHz的多种波形,转轴到机壳间电压即轴电压,可通过DS1204B型示波器探头测量,示波器品牌为RIGOL,轴电流采用Tektronix TCP312A型电流探头测量。

4.2 试验结果

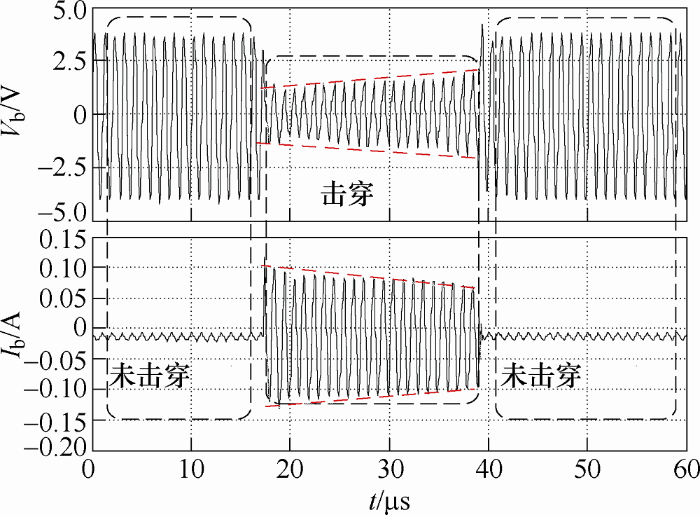
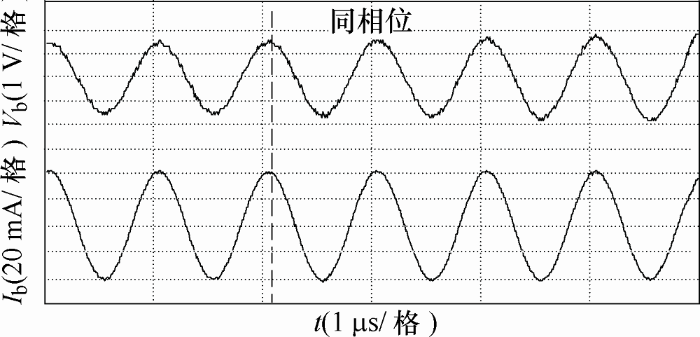
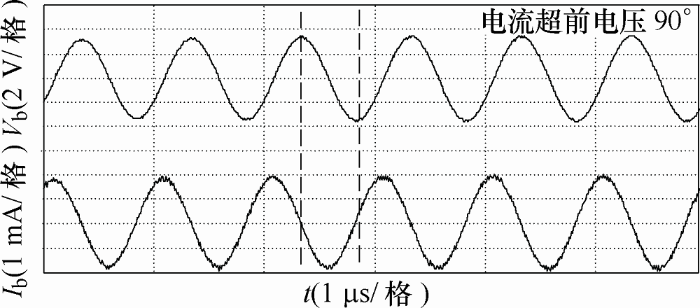
击穿几率随轴电压的升高而增加,所以为获得较为稳定的电压电流波形,本文选取正弦信号激励频率为f =1 MHz,电压峰峰值为Vpp=10 V。测得的轴电压Vb、轴电流Ib波形如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   试验测得的轴电压、轴电流波形


将击穿部分和未击穿部分的图放大,图8为击穿后的轴电压和轴电流波形,二者相位相同,接近为电阻状态;图9为未击穿时的波形,轴电流超前轴电压约90°,为电容状态。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   击穿后的轴电压、轴电流波形


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   未击穿时的轴电压、轴电流波形


4.3 可变电阻的参数提取

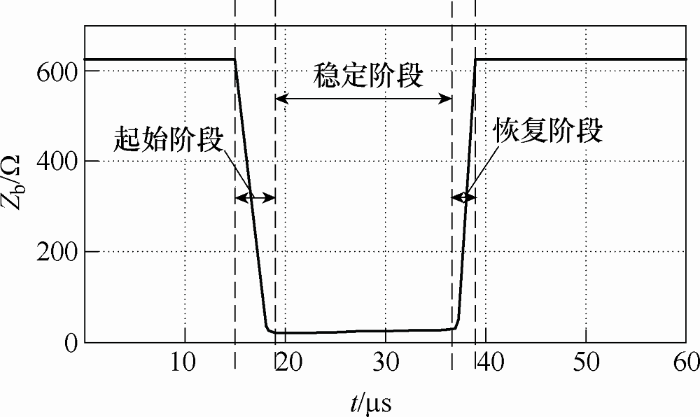
用同一时刻的电压除以电流,得到阻抗绝对值曲线如图10所示。从击穿到恢复可以分三个阶段：起始阶段、稳定阶段和恢复阶段。其中,未击穿阻抗r=628 Ω;稳定阶段的电阻值R0=28 Ω。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   实测阻抗曲线


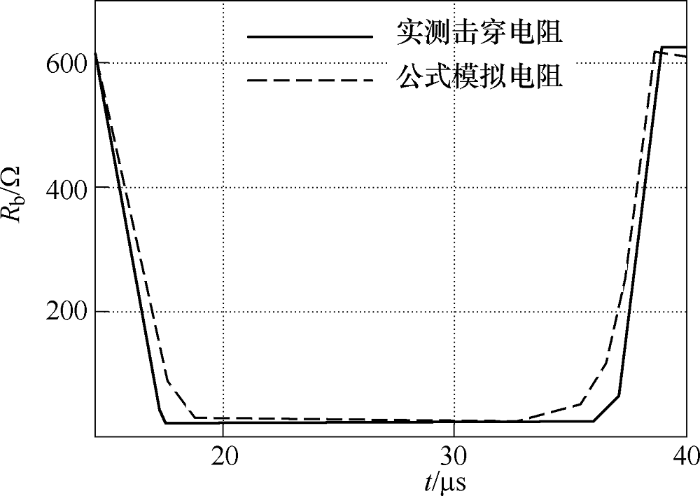
此处将未击穿时轴承的阻抗值r=628 Ω和击穿稳定时的电阻值R0=28 Ω代入式(3)~(4),可以计算得到可变击穿电阻曲线。将试验测得的电阻曲线和由本文提出的电阻模型计算出来的电阻曲线进行对比,如图11所示。可见击穿电阻的计算模型能较好地模拟击穿和恢复过程中等效电阻的变化趋势。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   等效电阻的实测和模拟曲线


以上提出了一种改进轴承等效模型,并给出了参数的计算方法。为验证其正确性,对可变电阻模型和恒定电阻模型进行仿真计算,并将其与实测轴电压轴电流模型进行对比验证。

5 可变电阻轴承等效模型仿真与验证

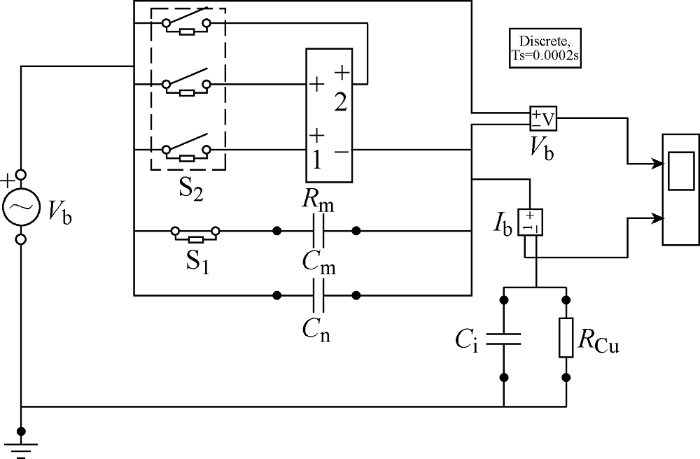
首先仿真可变电阻轴承等效模型施加正弦信号时的情况,仿真模型如图12所示。所加信号为Vb=10 V,f=1 MHz,Rm为可变电阻模块,Cm、Cn为图5中对应电容,Ci、RCu为考虑电机改装引入的绝缘电容和测量引线电阻,分别为RCu≈4.8 mΩ,Ci=25.49 pF[5]。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   轴承可变电阻模型仿真电路


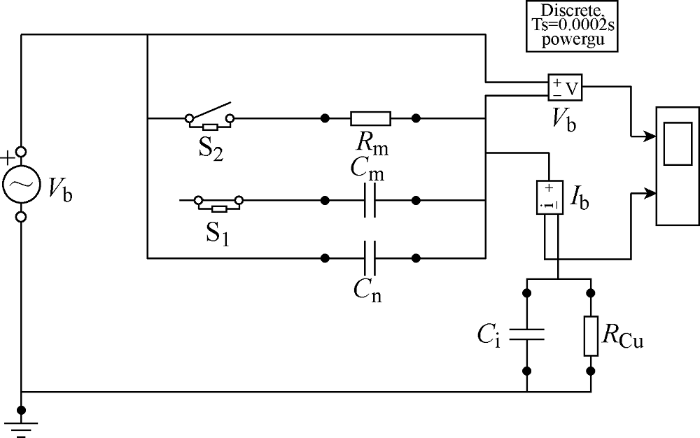
将图12中可变电阻轴承等效模型替换为恒定电阻轴承模型,如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   轴承恒定电阻模型仿真电路


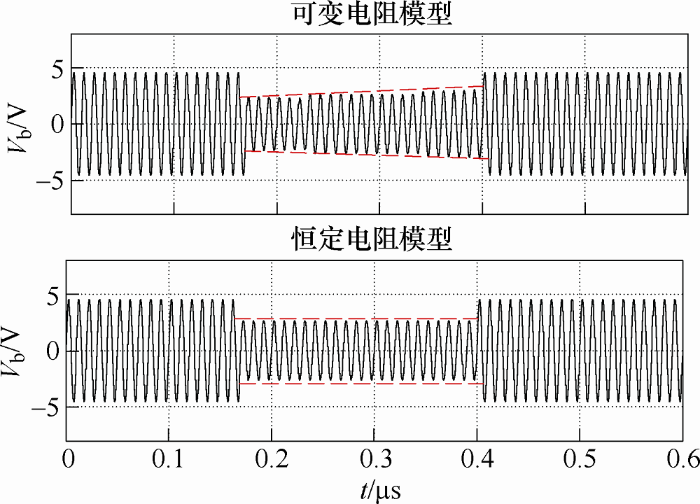
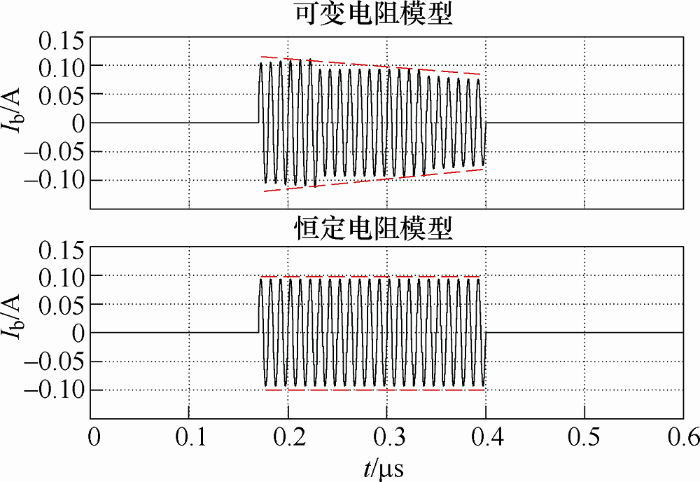
将两种仿真电路获得的轴电压、轴电流波形进行对比,如图14、15所示。分析两种情况下获得的波形图,未击穿时两种模型的轴电压和轴电流相同;但击穿以后呈现电阻状态,采用可变电阻的模型获得的轴电压呈现略微增加的趋势、轴电流在击穿以后呈现缓慢减少的趋势,而采用恒定电阻模型中,击穿以后电压和电流保持恒定不变。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   轴承可变电阻和恒定电阻模型轴电压仿真波形


图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   轴承可变电阻和恒定电阻模型轴电流仿真波形


通过试验得到的轴电压和轴电流波形(见图7)击穿以后也有缓慢变化的趋势,所以对比两种模拟电路得到的波形,可知采用可变电阻模型可以更为准确地模拟出了轴承击穿时的实际情况。在不同信号下做类似的实验,发现频率和电压越高,击穿电阻的变化幅度越大,此时为了准确预测轴电流,用可变电阻来模拟轴承也变得更加重要。

6 结论

本文主要对轴电流分析模型中的轴承模型及其参数进行了分析,得到以下结论。

(1) 从轴承的实际结构出发结合轴电流击穿实验测得的波形,提出轴承可变击穿电阻模型。

(2) 从电击穿的原理出发,结合电弧理论确定了击穿等效电阻的分段计算方法。

(3) 对比了恒定电阻模型和可变电阻模型,可变电阻模型仿真得到的轴承击穿过程更接近实验结果。

参考文献

姜艳姝 .

现代变频调速系统负面效应研究及其对策

[D]. 哈尔滨:哈尔滨理工大学, 2007.

[本文引用: 1]

姜保军 .

PWM电机驱动系统传导共模EMI抑制方法研究

[D]. 哈尔滨:哈尔滨工业大学, 2007.

[本文引用: 1]

Schiferl R F, Elfi M J .

Bearing current remediation options

[J]. IEEE Industry Applications Magazine, 2004,10(4):40-50.

[本文引用: 1]

Annette Muetze .

Bearing currents in inverter-fed AC-motors

[C].Technische Universitaet Darmstadt,Germany, 2004.

[本文引用: 1]

桑秉谦 .

变频供电交流电机轴电流的分析与测量

[D]. 北京:北京交通大学, 2016.

[本文引用: 8]

马喜平 .

PWM变频供电异步电机耦合电容计算与轴电流分析

[D]. 北京:北京交通大学, 2012.

[本文引用: 1]

Muetze A, Binder A .

Calculation of motor capacitances for prediction of discharge bearing currents in machines of inverter-based drive systems

[C]// IEEE Electric Machines and Drives, 2005,11(13):264-270.

[本文引用: 1]

Thusitha Randima Wellawatta, Jun-Kyu Park, Hak-Man Kim , et al.

New equivalent circuit of the IPM-type BLDC motor for calculation of shaft voltage by considering electric and magnetic fields

[C]// IEEE Energy Conversion Congress and Exposition (ECCE), 2015.

[本文引用: 1]

王禹, 白保东 .

分布参数共模等效电路关键参数确定及轴承电流计算

[J]. 电工技术学报, 2014,29(S1):124-131.

[本文引用: 1]

Wang Yu, Bai Baodong .

Determination of key parameters of common parameters equivalent circuit of distributed parameters and calculation of bearing current

[J]. Trans. China Electrotech. Soc., 2014,29(S1):124-131.

[本文引用: 1]

刘瑞芳, 娄卓夫, 马喜平 , 等.

电机轴电流问题中轴承等效电容和电阻的计算模型

[J]. 中国电机工程学报, 2014,34(15):2430-2437.

DOI:10.13334/j.0258-8013.pcsee.2014.15.013      URL     Magsci     [本文引用: 1]

在PWM逆变器供电交流电动机运行中, 轴电流问题影响着系统安全。预测轴电压和轴电流需要确定轴承的等效电容和电阻。该文通过分析轴承受到应力作用发生的弹性形变推导了轴承滚球与滚道之间的赫兹接触面积与油膜厚度的计算公式, 继而得出轴承电容的计算公式。通过该模型分析了轴承电容与电机轴承温度、电机转速和轴承受力之间的关系。推导了轴承等效击穿电阻的计算公式, 指出该等效电阻会随着油膜击穿点数的增大而减小。对一台变频供电2.2<sub></sub>kW感应电机进行轴电压和共模电压测量, 结果表明所提出的计算模型是合理的。

Liu Ruifang, Lou Zhuofu, Ma Xiping , et al.

Modeling of bearing capacitance and resistance in motor bearing current problem

[J]. Proceedings of CSEE, 2014,34(15):2430-2437.

DOI:10.13334/j.0258-8013.pcsee.2014.15.013      URL     Magsci     [本文引用: 1]

在PWM逆变器供电交流电动机运行中, 轴电流问题影响着系统安全。预测轴电压和轴电流需要确定轴承的等效电容和电阻。该文通过分析轴承受到应力作用发生的弹性形变推导了轴承滚球与滚道之间的赫兹接触面积与油膜厚度的计算公式, 继而得出轴承电容的计算公式。通过该模型分析了轴承电容与电机轴承温度、电机转速和轴承受力之间的关系。推导了轴承等效击穿电阻的计算公式, 指出该等效电阻会随着油膜击穿点数的增大而减小。对一台变频供电2.2<sub></sub>kW感应电机进行轴电压和共模电压测量, 结果表明所提出的计算模型是合理的。

马喜平 .

变频供电异步电机耦合电容的计算与轴电流的分析

[D]. 北京:北京交通大学, 2012.

[本文引用: 1]

刘瑞芳, 桑秉谦, 李伟力 .

交流电机轴承电容的计算与测量

[J]. 中国电机工程学报, 2017,37(10):2986-2993.

[本文引用: 2]

Liu Ruifang, Sang Bingqian, Li Weili .

Calculations and measurements of bearing capacitance in AC motor bearings

[J]. Proceedings of the CSEE, 2017,37(10):2986-2993.

[本文引用: 2]

Prashad H . Tribology in electrical environments[M]. Elsevier,Hyderabad,India, 2006.

[本文引用: 1]

Bartz M .

Lubricant film formation in grease lubricated high speed spindle bearings[D].

University of Hannover, Germany, 1996.

[本文引用: 1]

Busse D, Erdman J, Kerkman R J , et al.

System electrical parameters and their effects on bearing currents

[J]. IEEE Transactions on Industry Applications, 1997,33(2):577-584.

URL     [本文引用: 1]

Busse D, Erdman J, Kerkman R J , et al.

Bearing currents and their relationship to PWM drives

[J]. IEEE Trans. Power Electronics, 1997,12(2):243-252.

URL     [本文引用: 1]

薛锐 .

电火花放电通道的理论分析与放电间隙测试研究

[D]. 上海:上海交通大学, 2011.

[本文引用: 1]

张建功, 王红超, 赵军 , 等.

基于分段电弧模型的多次重燃弧VFTO计算与分析

[J]. 高压电器, 2016,52(5):14-19,26.

[本文引用: 2]

Zhang Jiangong, Wang Hongchao, Zhao Jun , et al.

Calculation and analysis of multiple reignition arc VFTO based on segmented arc model

[J]. High Voltage Apparatus, 2016,52(5):14-19,26.

[本文引用: 2]

/

〈 〉