1 引言
近年来,随着智能电网的迅速发展,负荷组成日趋多样化、精密化,对电能质量的要求越来越高;同时,各类非线性负荷的大量使用使得电网的电能质量也受到严重的影响[1 ] 。统一电能质量调节器(Unified Power Quality Conditioner,UPQC)由日本学者H. Akagi于1996年首次提出,可同时处理电压型和电流型电能质量问题,保证优秀的负载电压和电网电流品质,进而实现为电力用户提供安全、可靠电能的目的。因其具有综合的补偿功能,UPQC成为国内外学者研究的热点[2 ] 。作为UPQC装置的重要组成部分,补偿量的准确和实时检测是UPQC实现其综合补偿性能的重要前提。因此,对UPQC补偿量检测方法的研究具有重要意义。
目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] 。受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] 。当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差。文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢。目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] 。
针对以上问题,本文提出一种UPQC补偿量综合检测方法。该方法省去了锁相环,使得电路设计得以简化,解决了因使用锁相环而带来的误差问题;将平均值理论引入检测电路中,避免了LPF的使用,从而使检测的实时性得以提高;同时,将所提取出的电网基波正序电压的相位信息作为电流检测的相位基准,实现了电压、电流补偿量检测过程的统一。利用Matlab/Simulink搭建了仿真模型,仿真结果表明了该检测方法的可行性。
2 UPQC基本原理
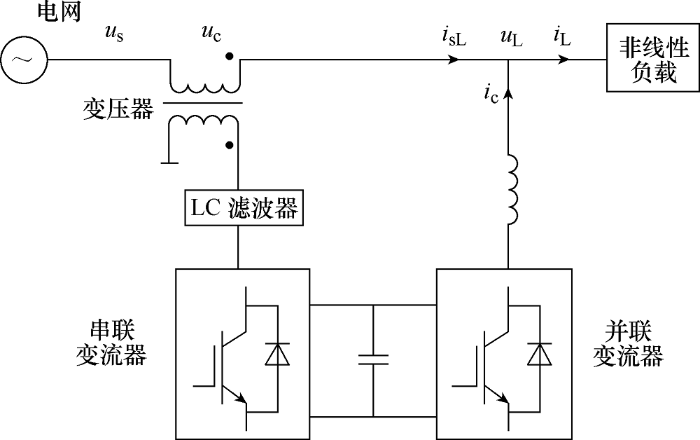
UPQC的基本拓扑结构如图1 所示。其主要由变压器、串联变流器及LC滤波器、直流母线电容器、并联变流器及其输出滤波电感器等部分组成。串联变流器通过变压器接入电网,主要功能是补偿电网电压的电能质量问题,如电压谐波和电压波动等;并联变流器通过输出滤波电感器直接并联在负载侧,主要功能是补偿负载电流的电能质量问题,如谐波电流和无功电流等。
图1
当电网电压偏离正常值时,需要由检测环节快速检测出电网电压中的畸变电压,即需要补偿的电压量,然后由串联变流器跟踪此电压补偿量并产生一个与其大小相等的补偿电压,通过变压器注入电网,从而使负载侧电压保持为标准正弦电压。电压补偿的计算式为
(1) ${{u}_{\text{L}}}={{u}_{\text{s}}}-{{u}_{\text{c}}}$
式中,u L 、u s 、u c 分别表示负载侧电压、实际电网电压和补偿电压。
当负载产生谐波电流、无功电流时,由检测环节快速检测出负载侧的畸变电流,即需要补偿的电流量,然后由并联变流器跟踪此电流补偿量并产生一个与其大小相等的补偿电流提供给负载,使网侧电流保持为标准正弦电流,从而防止非线性负载对网侧电流产生干扰。电流补偿的计算式为
(2) ${{i}_{\text{sL}}}={{i}_{\text{L}}}-{{i}_{\text{c}}}$
式中,i sL 、i L 、i c 分别表示网侧电流、实际负载电流和补偿电流。
可见,为实现UPQC良好的综合补偿性能,正常工作时对电压、电流补偿量检测的准确性和实时性具有很高的要求。因此,对UPQC补偿量检测方法的研究具有重要意义。
3 补偿量改进检测法
基于同步坐标变换的dq 检测法是将三相静止abc坐标系下的变量变换到两相旋转dq 坐标系下进行研究,但传统dq 检测法中由于锁相环和LPF的使用会带来一定的误差,因此本文提出改进的dq 检测法,省去锁相环,同时用平均值滤波法代替LPF获取直流分量,避免了锁相环引起的误差,同时提升检测的实时性。
3.1 无锁相环检测
在三相电压不对称情况下,电网电压的相位是由正序、负序和零序分量共同作用的结果,采用锁相环检测的是a相电压相位,与实际正序电压分量的相位存在相位差[10 ,11 ] ,进而影响检测的准确度;且锁相环的存在往往会使得实际电路的设计和调试变得复杂[12 ] ,因此,本文采用无锁相环的检测方法使检测电路得以简化。
传统ip -iq 检测法和dq 检测法中,锁相环的作用是获取变换矩阵中所需的正弦信号sinωt 和余弦信号cosωt ,即需要确定的是角频率ω 。为深入了解ω 在变换中所起的作用,以电网电压为例进行分析。
三相电压在不对称且发生畸变时,其在三相静止坐标系下可表示为
(3) $ \left\{\begin{aligned}{{u}_{\text{sa}}}=\sum\limits_{n=1}^{\infty }{[{{V}_{n+}}\sin (n\omega t+{{\theta }_{n+}})+{{V}_{n-}}\sin (n\omega t+{{\theta }_{n-}})+} \\{{V}_{n\text{0}}}\sin (n\omega t+{{\theta }_{n\text{0}}})] \\{{u}_{\text{sb}}}=\sum\limits_{n=1}^{\infty }{[{{V}_{n+}}\sin (n\omega t+{{\theta }_{n+}}-120{}^\circ )+{{V}_{n-}}\sin (n\omega t+} \\{{\theta }_{n-}}+120{}^\circ )+{{V}_{n\text{0}}}\sin (n\omega t+{{\theta }_{n\text{0}}})] \\{{u}_{\text{sc}}}=\sum\limits_{n=1}^{\infty }{[{{V}_{n+}}\sin (n\omega t+{{\theta }_{n+}}+120{}^\circ )+{{V}_{n-}}\sin (n\omega t+} \\{{\theta }_{n-}}-120{}^\circ )+{{V}_{n\text{0}}}\sin (n\omega t+{{\theta }_{n\text{0}}})]\end{aligned}\right.$
式中,u sa 、u sb 、u sc 分别为电网a、b、c相电压;V 为电压幅值;$\theta $为电压分量初相角;下标s为电网侧电量;n 为谐波次数。其中,+、-、0分别表示正序、负序和零序分量。
通过同步坐标变换矩阵将三相电压变换到两相旋转dq 坐标系中,即
(4) $\left[ \begin{matrix} {{u}_{\text{s}d}} \\ {{u}_{\text{s}q}} \\ \end{matrix} \right]={{C}_{\text{abc/}dq}}\left[ \begin{matrix} {{u}_{\text{sa}}} \\ {{u}_{\text{sb}}} \\ {{u}_{\text{sc}}} \\ \end{matrix} \right]$
${{C}_{\text{abc/dq}}}=\frac{2}{3}\left[ \begin{matrix} \begin{matrix} \cos \omega t \cos (\omega t-120{}^\circ ) \cos (\omega t+120{}^\circ ) \\ \end{matrix} \\ \begin{matrix} -\sin \omega t -\sin (\omega t-120{}^\circ ) -\sin (\omega t+120{}^\circ ) \\ \end{matrix} \\ \end{matrix} \right]$
(5) $\left[ \begin{matrix} {{u}_{\text{s}d}} \\ {{u}_{\text{s}q}} \\ \end{matrix} \right]=\left[ \begin{array}{*{35}{l}} \begin{matrix} {{V}_{1+}}\sin {{\theta }_{1+}}+\sum\limits_{n=2}^{\infty }{\left\{ {{V}_{n+}}\sin \left[ (n-1)\omega t+{{\theta }_{n+}} \right]+ \right.} \\ \left. {{V}_{n-}}\sin \left[ (n+1)\omega t+{{\theta }_{n-}} \right] \right\} \\ \end{matrix} \\ \begin{matrix} -{{V}_{1+}}\cos {{\theta }_{1+}}+\sum\limits_{n=2}^{\infty }{\left\{ -{{V}_{n+}}\cos \left[ (n-1)\omega t+{{\theta }_{n+}} \right]- \right.} \\ \left. {{V}_{n-}}\cos \left[ (n+1)\omega t+{{\theta }_{n-}} \right] \right\} \\ \end{matrix} \\ \end{array} \right] $
由式(5)可知,经过dq 变换后,仅基波正序分量转化为d 、q 轴上的直流分量,而第n 次正序分量转化为第n -1次交流分量,第n 次负序分量转化为第n +1次交流分量。通过LPF滤除交流分量,得到dq 坐标系下直流分量为
(6) $\left[ \begin{matrix} {{{\bar{u}}}_{sd}} \\ {{{\bar{u}}}_{sq}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{V}_{1+}}\sin {{\theta }_{1+}} \\ -{{V}_{1+}}\cos {{\theta }_{1+}} \\ \end{matrix} \right]$
将式(6)进行dq 反变换,可得到a、b、c三相的基波正序电压为
(7) $\left\{ \begin{array}{*{35}{l}} {{u}_{\text{af}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}) \\ {{u}_{\text{bf}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}-120{}^\circ ) \\ {{u}_{\text{cf}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}+120{}^\circ ) \\ \end{array} \right.$
假设变换矩阵C abc/ dq ω 为ω 0 ,则三相静止坐标系下的电网电压经过同步坐标变换后在dq 坐标系下的表达式为
(8) $\left[ \begin{matrix} {{{{u}'}}_{\text{s}d}} \\ {{{{u}'}}_{\text{s}q}} \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} \sum\limits_{n=1}^{\infty }{\left\{ {{V}_{n+}}\sin \left[ (n\omega -{{\omega }_{0}})t+{{\theta }_{n+}} \right]+ \right.} \\ \left. {{V}_{n-}}\sin \left[ (n\omega -{{\omega }_{0}})t+{{\theta }_{n-}} \right] \right\} \\ \end{matrix} \\ \begin{matrix} \sum\limits_{n=1}^{\infty }{\left\{ -{{V}_{n+}}\cos \left[ (n\omega -{{\omega }_{0}})t+{{\theta }_{n+}} \right]- \right.} \\ \left. {{V}_{n-}}\cos \left[ (n\omega -{{\omega }_{0}})t+{{\theta }_{n-}} \right] \right\} \\ \end{matrix} \\ \end{matrix} \right]$
若ω 与ω 0 的差值很小,低于LPF的截止频率,则通过LPF后可得
(9) $\left[ \begin{matrix} {{{{\bar{u}}'}}_{\text{s}d}} \\ {{{{\bar{u}}'}}_{\text{s}q}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{V}_{1+}}\sin \left[ (\omega -{{\omega }_{0}})t+{{\theta }_{1+}} \right] \\ -{{V}_{1+}}\cos \left[ (\omega -{{\omega }_{0}})t+{{\theta }_{1+}} \right] \\ \end{matrix} \right]$
由式(9)可知,此时通过LPF后得到的分量为频率较低的交流量,而非直流。若对式(9)进行dq 反变换,可得
(10) $\left\{ \begin{array}{*{35}{l}} {{{{u}'}}_{\text{af}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}) \\ {{{{u}'}}_{\text{bf}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}-120{}^\circ ) \\ {{{{u}'}}_{\text{cf}}}={{V}_{1+}}\sin (\omega t+{{\theta }_{1+}}+120{}^\circ ) \\ \end{array} \right.$
式(10)和式(7)结果完全相同,表明ω 0 仅在变换过程中起作用,对最终的检测结果不会造成影响[10 ] 。因此,若能够确定一个与实际频率相接近的值,即可检测出补偿量。
由于我国电力系统中的电网工频为50Hz,且规定允许的频率偏差为不超过±(0.2~0.5)Hz[13 ] ,故可直接取ω 0 =2πf 0 = 100π rad/s,省去了锁相环,既简化了检测电路,也避免了因使用锁相环而引起的误差问题。
3.2 改进的平均值滤波法
传统的ip -iq 检测法和dq 检测法中,一般通过使用LPF滤除交流分量,从而获取相应的直流分量。而在实际中LPF的实现较为复杂,且存在滤波精度低、动态响应速度慢的缺点[14 ] 。因此本文采用基于平均值理论的方法代替LPF以获取相应的直流分量,相比使用LPF具有更快的响应速度,且易于实现。
(11) $\bar{y}=\frac{1}{T}\int_{t}^{t+T}{x\text{d}t}$
由于三相电压、电流中的基波分量对应于dq 坐标系下的直流分量,谐波分量对应于交流分量,而交流分量在一个交流周期内的平均值为零,因此采用式(11)平均值滤波法可滤除交流分量,从而获取与基波分量所对应的直流分量。
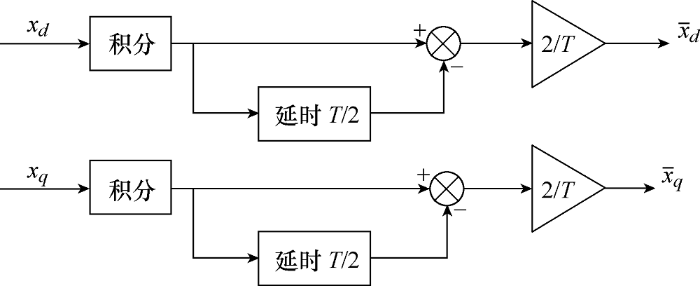
通过式(11)能够滤除交流分量,但由于积分周期为T ,即需要对输入量进行一个基波周期T 的积分,因此对响应速度会有影响。若将积分周期设为各次交流分量周期的最小公倍数,同样能够完全滤除交流分量,达到获取直流分量的目的。
(12) $\left\{ \begin{array}{*{35}{l}} {{i}_{\text{La}}}=\sum\limits_{n=1}^{\infty }{\left[ {{I}_{n+}}\sin (n\omega t+{{\varphi }_{n+}})+{{I}_{n-}}\sin (n\omega t+{{\varphi }_{n-}}) \right]} \\ \begin{matrix} {{i}_{\text{Lb}}}=\sum\limits_{n=1}^{\infty }{\left[ {{I}_{n+}}\sin (n\omega t+{{\varphi }_{n+}}-120{}^\circ )+ \right.} \\ \left. {{I}_{n-}}\sin (n\omega t+{{\varphi }_{n-}}+120{}^\circ ) \right] \\ \end{matrix} \\ \begin{matrix} {{i}_{\text{Lc}}}=\sum\limits_{n=1}^{\infty }{\left[ {{I}_{n+}}\sin (n\omega t+{{\varphi }_{n+}}+120{}^\circ )+ \right.} \\ \left. {{I}_{n-}}\sin (n\omega t+{{\varphi }_{n-}}-120{}^\circ ) \right] \\ \end{matrix} \\ \end{array} \right.$
式中,I 为电流幅值;$\varphi $为初相角;下标L表示负载侧的电量,+、-分别表示正序、负序分量。
(13) $\left[ \begin{matrix} {{i}_{d}} \\ {{i}_{q}} \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} \sum\limits_{n=1}^{\infty }{\left\{ {{I}_{n+}}\sin \left[ (n-1)\omega t+{{\varphi }_{n+}} \right]+ \right.} \\ \left. {{I}_{n-}}\sin \left[ (n+1)\omega t+{{\varphi }_{n-}} \right] \right\} \\ \end{matrix} \\ \begin{matrix} -\sum\limits_{n=1}^{\infty }{\left\{ {{I}_{n+}}\cos \left[ (n-1)\omega t+{{\varphi }_{n+}} \right]+ \right.} \\ \left. {{I}_{n-}}\cos \left[ (n+1)\omega t+{{\varphi }_{n-}} \right] \right\} \\ \end{matrix} \\ \end{matrix} \right]$
选用带阻感负载的二极管不可控整流桥作为非线性负载时,负载产生的谐波次数为n =6k ±1次,其中k 为整数(k =0时,只取+号)。于是将式(13)展开可得
(14) $\left[ \begin{matrix} {{i}_{d}} \\ {{i}_{q}} \\\end{matrix} \right]=\begin{equation*}\begin{bmatrix}{{I}_{1+}}\sin {{\varphi }_{1+}}+{{I}_{1-}}\sin (2\omega t+{{\varphi }_{1-}})+{{I}_{5+}}\sin (4\omega t\\+{{\varphi }_{5+}})+{{I}_{5-}}\sin (6\omega t+{{\varphi }_{5-}})+{{I}_{7+}}\sin (6\omega t\\+{{\varphi }_{7+}})+{{I}_{7-}}\sin (8\omega t+{{\varphi }_{7-}})+\cdot \cdot \cdot\\-{{I}_{1+}}\cos {{\varphi }_{1+}}-{{I}_{1-}}\cos (2\omega t+{{\varphi }_{1-}})-{{I}_{5+}}\cos (4\omega t\\+{{\varphi }_{5+}})-{{I}_{5-}}\cos (6\omega t+{{\varphi }_{5-}})-{{I}_{7+}}\cos (6\omega t\\+{{\varphi }_{7+}})-{{I}_{7-}}\cos (8\omega t+{{\varphi }_{7-}})+\cdot \cdot \cdot\\\end{bmatrix}\end{equation*}$
由式(14)可知,id 、iq 中的交流分量均为第2、4、6、8次等偶次分量,因此将d 、q 轴滤波环节中的积分周期设为T /2,即可实现将交流分量完全滤除的目的,并且能进一步提高检测的实时性。
(15) $\left\{ \begin{matrix} {{{\bar{x}}}_{d}}=\frac{2}{T}\int_{t}^{t+T\text{/2}}{{{x}_{d}}\text{d}t} \\ {{{\bar{x}}}_{q}}=\frac{2}{T}\int_{t}^{t+T\text{/2}}{{{x}_{q}}\text{d}t} \\ \end{matrix} \right.$
图2
3.3 改进综合检测法
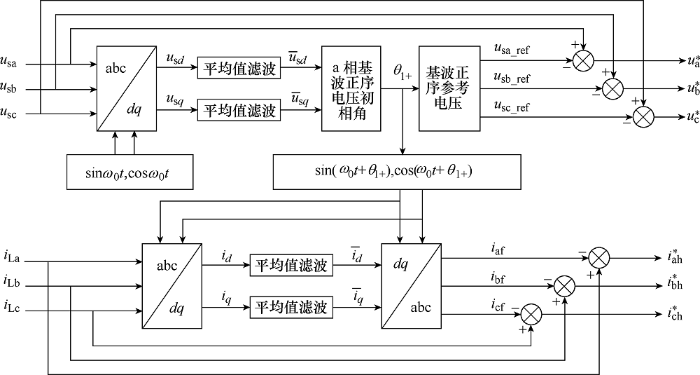
传统dq 检测法中因使用锁相环和LPF会带来一定的误差,因此本文提出改进的dq 检测法,采用无锁相环检测,并且用改进后的平均值滤波法代替LPF;同时将电压检测提取出的电网基波正序电压的相位信息作为电流检测的相位基准,即对电压、电流进行统一检测,以保证系统的稳定性。
图3
首先通过同步坐标变换矩阵将三相abc坐标系下的电网电压变换到两相旋转dq 坐标系下,得到u s d u s q u s d u s q
在获取到dq 坐标系下的直流分量后,进而得到基波正序电压分量的幅值及其初相角分别为
(16) $\left\{ \begin{align} {{u}_{\text{m}}}=\sqrt{\bar{u}_{\text{s}d}^{2}+\bar{u}_{\text{s}q}^{2}} \\ {{\theta }_{\text{1}+}}=\arctan ({{{\bar{u}}}_{\text{s}q}}/{{{\bar{u}}}_{\text{s}d}}) \\ \end{align} \right.$
由于实际电路中往往会存在线路损耗、电压跌落和电压突变等情况,因此本文直接将参考电压幅值设为电网额定电压幅值,于是得到基波正序参考电压为
(17) $\left\{ \begin{align} {{u}_{\text{sa }\!\!\_\!\!\text{ ref}}}=220\sqrt{2}\sin (\omega t+{{\theta }_{\text{1}+}}) \\ {{u}_{\text{sb }\!\!\_\!\!\text{ ref}}}=220\sqrt{2}\sin (\omega t+{{\theta }_{\text{1}+}}-120{}^\circ ) \\ {{u}_{\text{sc }\!\!\_\!\!\text{ ref}}}=220\sqrt{2}\sin (\omega t+{{\theta }_{\text{1}+}}+120{}^\circ ) \\ \end{align} \right.$
最后,将实际电网电压与所得基波正序参考电压作差即可得到电压补偿量。同时,将检测所得的电网基波正序电压的相位信息作为电流检测的相位基准,电流检测中采用改进dq 检测法,实现电压、电流的统一检测,最终检测出电压、电流补偿量。
4 仿真分析
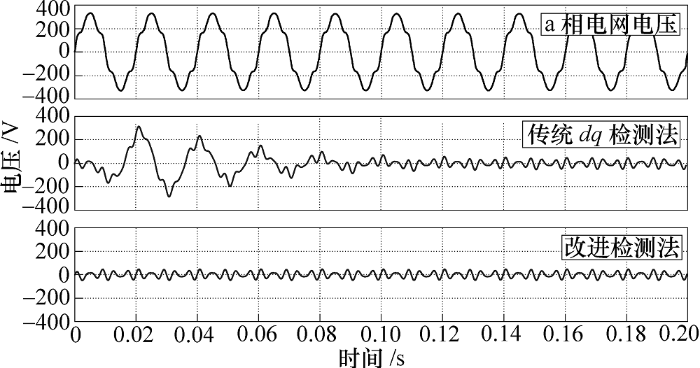
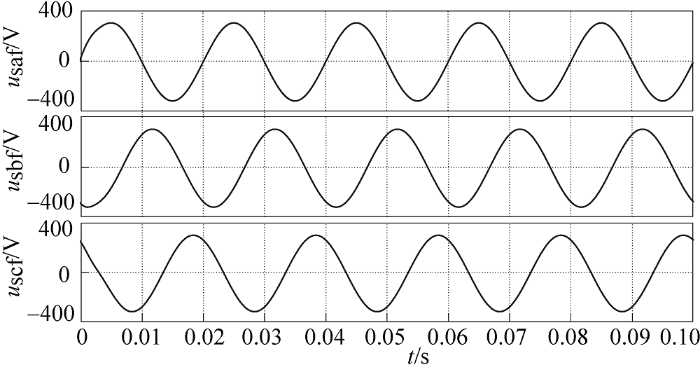
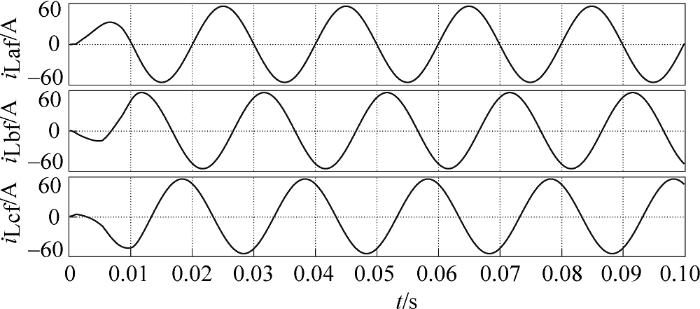
为验证本文改进检测法的可行性,利用Matlab/ Simulink搭建仿真模型,并与传统dq 检测法进行对比。设置三相对称电网电压有效值为220 V,频率为50 Hz,加入10%的5次谐波和5%的7次谐波;选取带阻感负载的三相不可控整流桥电路作为非线性负载,负载侧电感值为5 mH,电阻值为10$\Omega $。仿真结果分别如图4 ~图7 所示。
图4
图4
a相电网电压和分别采用传统dq 检测法、改进检测法得到的补偿电压
图5
图5
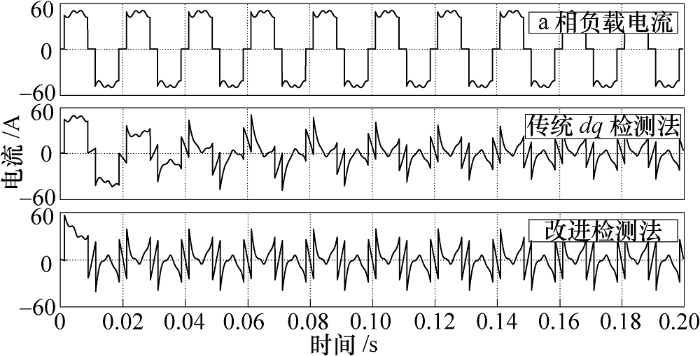
a相负载电流和分别采用传统dq 检测法、改进检测法得到的补偿电流
图6
图7
由图4 、图5 可知,采用传统dq 检测法分离出稳定的电压电流补偿指令需要超过两个周期的时间,而采用改进检测法仅需半个周期便能分离出稳定的电压电流补偿指令,具有更快的动态响应速度,检测实时性较好;图6 、图7 分别为采用传统dq 检测法和改进检测法测得的a相基波电压、电流波形,同样可以看出改进检测法相比传统dq 检测法具有更快的响应速度,并且改进检测法简化了检测电路,更容易实现。
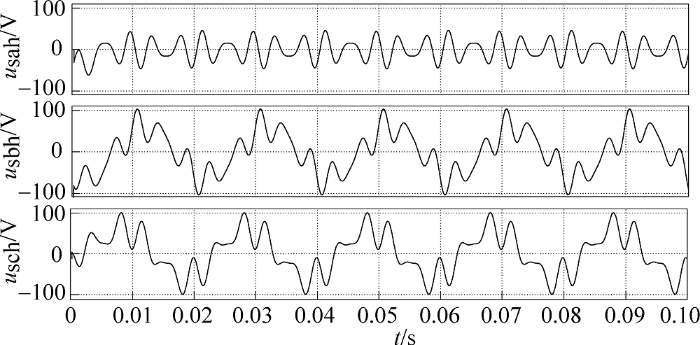
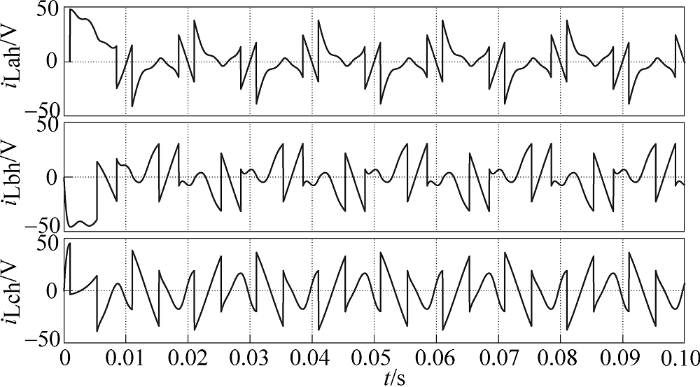
为验证改进检测法在三相不对称系统中的可行性,在三相电网电压不对称且畸变的情况下对其进行仿真。设置a相为标准电压幅值,b相电压幅值设为标准幅值的1.1倍,c相设为标准幅值的0.9倍,同时加入10%的5次谐波和5%的7次谐波。采用改进综合检测法的仿真结果如图8 ~图12 所示。
图8
图9
图10
图11
图12
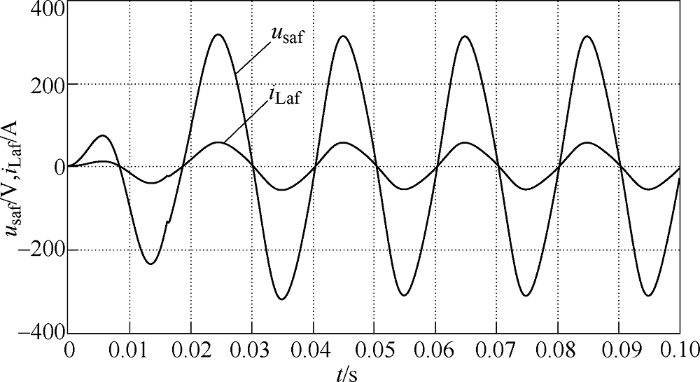
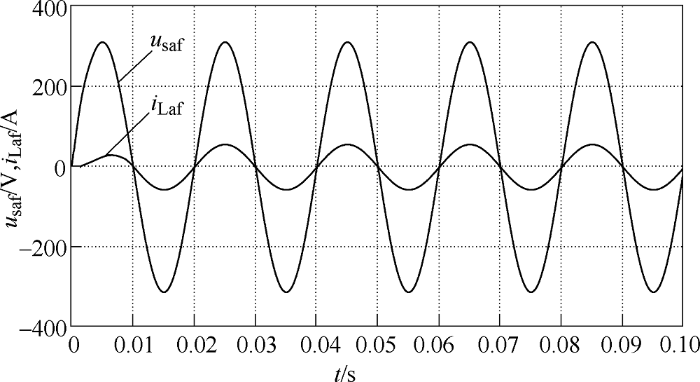
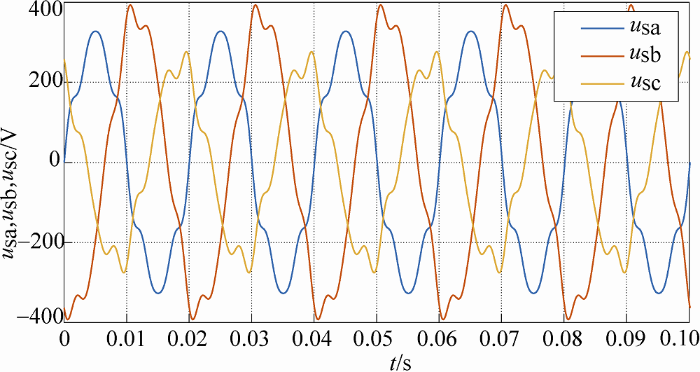
图8 为三相电网电压波形,可以看到三相电压发生畸变且幅度不平衡;图9 为分离出的电网基波正序电压;图10 为分离出的三相负载基波电流波形,可以看到仅在半个周期便检测出稳定基波电流,动态响应速度快,实时性好,并且各相的相位与三相基波正序电压的相位保持一致;图11 、图12 分别为检测得到的电压、电流畸变量,即电压、电流补偿量。图8 ~图12 仿真结果表明了改进补偿量检测法在三相电压不对称且发生畸变的情况下仍然可行。
5 结论
在三相电压不对称或发生畸变时,传统基于瞬时无功功率理论的一些检测方法因使用锁相环和LPF会导致检测结果存在一定误差,并且检测的实时性较差。针对以上问题,本文提出一种无锁相环的UPQC电压、电流补偿量改进检测法,使用改进平均值滤波法代替了LPF,简化了检测电路且提高了检测的响应速度;并将电网基波正序电压的相位信息作为电流检测的相位基准,使得电压和电流补偿量的检测过程得到了统一。理论推导和仿真结果表明了改进检测法的可行性。
参考文献
View Option
[1]
肖湘宁 . 电能质量分析与控制 [M]. 北京 : 中国电力出版社 , 2014 .
[本文引用: 1]
[2]
王久和 . 统一电能质量调节器控制策略研究
[J]. 发电技术 , 2018 ,39 (4 ):313 -321 .
[本文引用: 1]
Wang Jiuhe . Research on control strategy of unified power quality conditioner
[J]. Power Generation Technology , 2018 ,39 (4 ):313 -321 .
[本文引用: 1]
[3]
Zheng C C Wang J H The method of harmonic compensation of UPQC based on Euler-Lagrange model
[C]. IEEE Power Electronics and Motion Control Conference , 2016 : 142 -146 .
[本文引用: 2]
[4]
王久和 , 孙凯 , 张巧杰 . 统一电能质量调节器及其无源控制 [M]. 北京 : 机械工业出版社 , 2018 .
[本文引用: 1]
[5]
Wang B Xiong W Liu D . The comparative analysis of voltage sag detection based on dq transform method
[J]. Electrical Engineering , 2015 (7 ).
[本文引用: 1]
[6]
慕小斌 , 王久和 , 孙凯 . 非正弦不平衡电流全参量的检测方法
[J]. 电力系统自动化 , 2014 ,38 (13 ):160 -165 .
DOI:10.7500/AEPS20131013005
Magsci
[本文引用: 1]
为了克服传统检测方法在非正弦不平衡系统中检测的单一性,在对称分量法基础上提出一种计算矩阵,可将任意次的正、负、零序电流,广义无功电流,以及各相中的不平衡谐波、不平衡有功、不平衡无功电流,单相基波功率因数等参量一次计算出来。该方法的原理是在检测出基波不平衡电流的基础上利用幅相计算原理建立计算矩阵,即可方便计算出多种电参量。该方法可用于三相三线(四线)制和单相系统中,对电力系统自动化装置的检测及各种拓扑结构的电能质量治理装置的补偿量检测也适用,尤其在要考虑装置补偿容量以及装置能否补偿有功功率不平衡时可进行灵活选择补偿。理论分析和算例实验均表明了该方法的正确性和可行性。
Mu Xiaobin Wang Jiuhe Sun Kai . A detection method of non-sinusoidal and imbalanced currents
[J]. Automation of Electric Power Systems , 2014 ,38 (13 ):160 -165 .
DOI:10.7500/AEPS20131013005
Magsci
[本文引用: 1]
为了克服传统检测方法在非正弦不平衡系统中检测的单一性,在对称分量法基础上提出一种计算矩阵,可将任意次的正、负、零序电流,广义无功电流,以及各相中的不平衡谐波、不平衡有功、不平衡无功电流,单相基波功率因数等参量一次计算出来。该方法的原理是在检测出基波不平衡电流的基础上利用幅相计算原理建立计算矩阵,即可方便计算出多种电参量。该方法可用于三相三线(四线)制和单相系统中,对电力系统自动化装置的检测及各种拓扑结构的电能质量治理装置的补偿量检测也适用,尤其在要考虑装置补偿容量以及装置能否补偿有功功率不平衡时可进行灵活选择补偿。理论分析和算例实验均表明了该方法的正确性和可行性。
[7]
孙驰 , 魏光辉 , 毕增军 . 基于同步坐标变换的三相不对称系统的无功与谐波电流的检测
[J]. 中国电机工程学报 , 2003 ,23 (12 ):43 -48 .
[本文引用: 1]
Sun Chi Wei Guanghui Bi Zengjun . Detection of reactive power and harmonic current for three-phase asymmetric systems based on synchronous coordinate transformation
[J]. Proceedings of the CSEE , 2003 ,23 (12 ):43 -48 .
[本文引用: 1]
[8]
Li Z B Li C S Yan D , et al . A harmonic detection method by separated sequence and order suitable for novel direct AC-AC based active power filters
[J]. Proceedings of the CSEE , 2015 ,35 (6 ):1473 -1481 .
[本文引用: 1]
[9]
祝贺 , 王久和 , 郑成才 , 等 . 五电平MMC-UPQC的无源控制
[J]. 电工技术学报 , 2017 ,32 (S2 ):172 -178 .
[本文引用: 1]
Zhu He Wang Jiuhe Zheng Chengcai , et al . Passivity based control of five-level MMC-UPQC
[J]. Transactions of China Electrotechnical Society , 2017 ,32 (S2 ):172 -178 .
[本文引用: 1]
[10]
周海亮 . 统一电能质量调节器检测与补偿控制策略研究
[D]. 天津:天津大学 , 2012 .
[本文引用: 2]
[11]
Wu C Chang X . A compensation current detection method of D-STATCOM without phase-locked loop
[J]. Electric Power Science & Engineering , 2014 .
[本文引用: 1]
[12]
Li Z K Wang J Zhang F , et al . Rapid detection method for voltage sag without phase locked loop
[J]. High Voltage Engineering , 2016 ,42 (4 ):1326 -1335 .
[本文引用: 1]
[13]
林海雪 . 电压电流频率和电能质量国家标准应用手册 [M]. 北京 : 中国电力出版社 , 2001 .
[本文引用: 1]
[14]
Zhou J Wang Z Fu X Study on the improved harmonic detection algorithm based on FBD theory
[C]. IEEE Computer Society Asia-Pacific Power and Energy Engineering Conference , 2011 : 1 -4 .
[本文引用: 1]
1
2014
... 近年来,随着智能电网的迅速发展,负荷组成日趋多样化、精密化,对电能质量的要求越来越高;同时,各类非线性负荷的大量使用使得电网的电能质量也受到严重的影响[1 ] .统一电能质量调节器(Unified Power Quality Conditioner,UPQC)由日本学者H. Akagi于1996年首次提出,可同时处理电压型和电流型电能质量问题,保证优秀的负载电压和电网电流品质,进而实现为电力用户提供安全、可靠电能的目的.因其具有综合的补偿功能,UPQC成为国内外学者研究的热点[2 ] .作为UPQC装置的重要组成部分,补偿量的准确和实时检测是UPQC实现其综合补偿性能的重要前提.因此,对UPQC补偿量检测方法的研究具有重要意义. ...
统一电能质量调节器控制策略研究
1
2018
... 近年来,随着智能电网的迅速发展,负荷组成日趋多样化、精密化,对电能质量的要求越来越高;同时,各类非线性负荷的大量使用使得电网的电能质量也受到严重的影响[1 ] .统一电能质量调节器(Unified Power Quality Conditioner,UPQC)由日本学者H. Akagi于1996年首次提出,可同时处理电压型和电流型电能质量问题,保证优秀的负载电压和电网电流品质,进而实现为电力用户提供安全、可靠电能的目的.因其具有综合的补偿功能,UPQC成为国内外学者研究的热点[2 ] .作为UPQC装置的重要组成部分,补偿量的准确和实时检测是UPQC实现其综合补偿性能的重要前提.因此,对UPQC补偿量检测方法的研究具有重要意义. ...
统一电能质量调节器控制策略研究
1
2018
... 近年来,随着智能电网的迅速发展,负荷组成日趋多样化、精密化,对电能质量的要求越来越高;同时,各类非线性负荷的大量使用使得电网的电能质量也受到严重的影响[1 ] .统一电能质量调节器(Unified Power Quality Conditioner,UPQC)由日本学者H. Akagi于1996年首次提出,可同时处理电压型和电流型电能质量问题,保证优秀的负载电压和电网电流品质,进而实现为电力用户提供安全、可靠电能的目的.因其具有综合的补偿功能,UPQC成为国内外学者研究的热点[2 ] .作为UPQC装置的重要组成部分,补偿量的准确和实时检测是UPQC实现其综合补偿性能的重要前提.因此,对UPQC补偿量检测方法的研究具有重要意义. ...
The method of harmonic compensation of UPQC based on Euler-Lagrange model
2
2016
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
... [3 ];在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
1
2018
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
The comparative analysis of voltage sag detection based on dq transform method
1
2015
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
非正弦不平衡电流全参量的检测方法
1
2014
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
非正弦不平衡电流全参量的检测方法
1
2014
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
基于同步坐标变换的三相不对称系统的无功与谐波电流的检测
1
2003
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
基于同步坐标变换的三相不对称系统的无功与谐波电流的检测
1
2003
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
A harmonic detection method by separated sequence and order suitable for novel direct AC-AC based active power filters
1
2015
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
五电平MMC-UPQC的无源控制
1
2017
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
五电平MMC-UPQC的无源控制
1
2017
... 目前,应用较为广泛的补偿量检测方法为基于瞬时无功功率理论的p -q 检测法、ip -iq 检测法以及dq 检测法[3 ,4 ,5 ] .受诸多因素的影响,电力系统在实际运行过程中,电网中的电压往往会产生一定程度的畸变,且三相电压不对称也是普遍存在的现象[6 ] .当三相电压不对称或发生畸变时,采用p -q 检测法得到的补偿量均会偏离真实值,从而产生较大的检测误差[3 ] ;在三相电压发生畸变时,采用ip -iq 检测法可得到准确的检测结果,但当三相电压不对称时对基波有功和无功分量的检测将会存在误差[7 ] ;与ip -iq 检测法类似,dq 检测法同样无法避免因使用锁相环而引起的误差.文献[8 ]提出了一种基于对称分量法的无锁相环检测方法,能实时分解出基波正序分量,省去了锁相环及其相关电路,但计算过程较为繁琐,且由于低通滤波器(Low Pass Filter,LPF)的使用,检测的动态响应速度较慢.目前用于UPQC的检测方法多为将电压、电流补偿量分别进行检测,但UPQC作为一个整体系统,电压和电流二者之间的相位信息存在一定联系,因此应当将电压、电流进行统一检测,否则容易造成系统的控制不稳定[9 ] . ...
统一电能质量调节器检测与补偿控制策略研究
2
2012
... 在三相电压不对称情况下,电网电压的相位是由正序、负序和零序分量共同作用的结果,采用锁相环检测的是a相电压相位,与实际正序电压分量的相位存在相位差[10 ,11 ] ,进而影响检测的准确度;且锁相环的存在往往会使得实际电路的设计和调试变得复杂[12 ] ,因此,本文采用无锁相环的检测方法使检测电路得以简化. ...
... 式(10)和式(7)结果完全相同,表明ω 0 仅在变换过程中起作用,对最终的检测结果不会造成影响[10 ] .因此,若能够确定一个与实际频率相接近的值,即可检测出补偿量. ...
A compensation current detection method of D-STATCOM without phase-locked loop
1
2014
... 在三相电压不对称情况下,电网电压的相位是由正序、负序和零序分量共同作用的结果,采用锁相环检测的是a相电压相位,与实际正序电压分量的相位存在相位差[10 ,11 ] ,进而影响检测的准确度;且锁相环的存在往往会使得实际电路的设计和调试变得复杂[12 ] ,因此,本文采用无锁相环的检测方法使检测电路得以简化. ...
Rapid detection method for voltage sag without phase locked loop
1
2016
... 在三相电压不对称情况下,电网电压的相位是由正序、负序和零序分量共同作用的结果,采用锁相环检测的是a相电压相位,与实际正序电压分量的相位存在相位差[10 ,11 ] ,进而影响检测的准确度;且锁相环的存在往往会使得实际电路的设计和调试变得复杂[12 ] ,因此,本文采用无锁相环的检测方法使检测电路得以简化. ...
1
2001
... 由于我国电力系统中的电网工频为50Hz,且规定允许的频率偏差为不超过±(0.2~0.5)Hz[13 ] ,故可直接取ω 0 =2πf 0 = 100π rad/s,省去了锁相环,既简化了检测电路,也避免了因使用锁相环而引起的误差问题. ...
Study on the improved harmonic detection algorithm based on FBD theory
1
2011
... 传统的ip -iq 检测法和dq 检测法中,一般通过使用LPF滤除交流分量,从而获取相应的直流分量.而在实际中LPF的实现较为复杂,且存在滤波精度低、动态响应速度慢的缺点[14 ] .因此本文采用基于平均值理论的方法代替LPF以获取相应的直流分量,相比使用LPF具有更快的响应速度,且易于实现. ...