1 引言
传统永磁同步电机DTC方法首次提出时,定子磁链和电机转矩均由非零矢量控制,转矩脉动较大,为了改善稳态转矩性能,提高转速的稳定性,文献[1]将零矢量引入到转矩调节器中,实验结果表明,引入零矢量后,电机稳态转矩性能得到显著改善,但是文献[1]只是定性地提出将零矢量引入到转矩调节器中,并没有涉及转矩调节器的定量优化设计。为了进一步进行定量设计,就必须知道在数字控制条件下零矢量对永磁同步电机定子磁链幅值、转矩角以及转矩的影响,并进行详细定量的分析,为转矩调节器设计奠定一个坚实的理论基础[2]。本文将主要针对上述问题展开分析和研究,并在分析传统正弦波永磁同步电机DTC转矩变化规律的基础上提出一种转矩调节器设计方法。
2 PMSM直接转矩控制原理
2.1 转矩控制原理分析
传统正弦波永磁同步电机 DTC方法通过选择空间电压矢量实现对电机磁链和转矩的闭环控制[3]。对于隐极式正弦波永磁同步电机,其转矩为
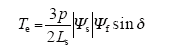
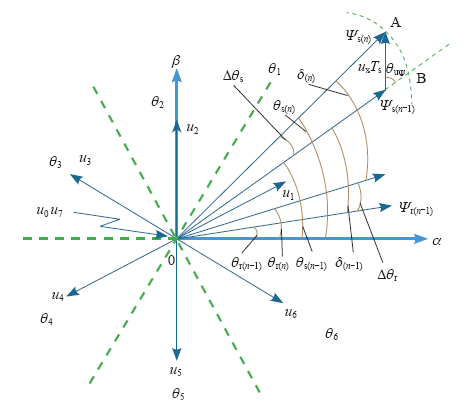
以定转子磁链位于θ1扇区为例,当选择目标空间电压矢量作用于电机后,控制周期内定转子磁链和转矩角的变化情况如图1所示。
图1
图1
控制周期内定转子磁链和转矩角变化情况
Fig.1
Variation of stator, rotor flux linkage and power angle during the control cycle
图中,ux为控制周期内选择的目标空间电压矢量,Ts为控制周期,θuΨ为目标空间电压矢量和控制周期开始前定子磁链之间的夹角,Ψs(n-1)和Ψs(n)分别为空间电压矢量作用前后的定子磁链,Δθs为控制周期内定子磁链位置的变化量。图中,OA线段长度等于OB线段长度,为定子磁链Ψs(n)幅值的大小。Ψr(n-1)和Ψr(n)分别为空间电压矢量作用前后的转子永磁体磁链,二者幅值相等,位置不同,Δθr为控制周期内转子磁链位置的变化量。θs(n-1)和θs(n)分别为控制周期前后定子磁链相对于α轴的角度。θr(n-1)和θr(n)分别为控制周期前后转子磁链相对于α轴的角度。δ(n-1)和δ(n)分别为控制周期前后定转子磁链之间的夹角,即转矩角[4]。
从图1可知,在空间电压矢量作用的一个控制周期内,电机定子磁链幅值和转矩角均发生了变化,结合隐极式正弦波永磁同步电机转矩表达式(1),得到电机转矩变化的全微分表达式为
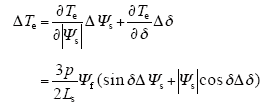
式中,ΔΨs和Δδ分别为控制周期内定子磁链幅值和转矩角的变化量。从式(1)可知,电机转矩的变化取决于定子磁链幅值和转矩角二者共同作用的结果[5]。下面分别对二者的变化规律以及对转矩变化的影响进行分析。
电机稳定运行过程中,在图1所示的扇区内,当选择空间电压矢量u2和u3增加转矩时,控制周期内定子磁链幅值的变化量可近似表示为
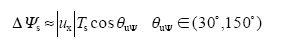
正弦波永磁同步电机DTC中定转子磁链之间的夹角定义为转矩角,转矩角和定转子磁链角度有关,三者之间有如下关系成立,即
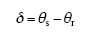
由图1可知,控制周期内定转子磁链位置的变化取决于二者控制周期前后的位置,并满足如下关系
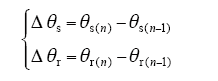
电机稳定运行过程中,控制周期内Δθs很小,从图1可知,Δθs可近似表示为
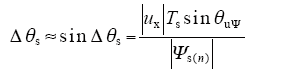
而控制周期内转子磁链位置的变化则取决于电机转速,则Δθr可表示为
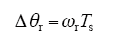
根据式(4)~式(7)可得控制周期内转矩角的变化如下为
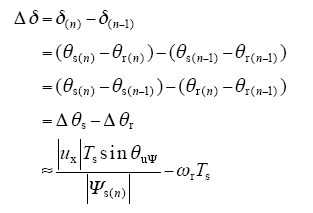
将式(1)离散化可得控制周期内转矩变化为
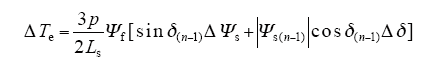
根据前面对控制周期内定子磁链和转矩角的分析结果,将式(3)、式(8)代入式(9)得到如下分析过程
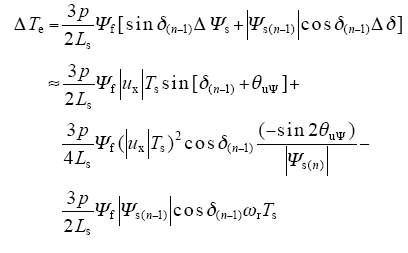
从式(10)中的分析结果可知,控制周期内电机转矩的变化和电机极对数、电机电感、转子磁链、空间电压矢量的大小、控制周期的长短、定子磁链的变化以及转矩角的变化有关[6]。为便于分析,不妨令
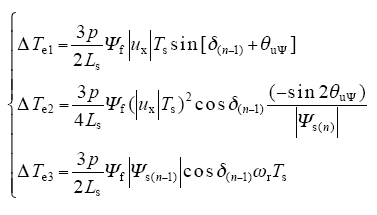
2.2 DTC中零矢量的作用
转矩调节器中既然要引入零矢量,那么首先要分析零矢量对电机转矩的具体作用。当选择零矢量作用于电机后,在忽略定子电阻压降的情况下,定子磁链的幅值和相位均不变,从对转矩角的分析过程可知,转矩角的变化取决于定子磁链和转子磁链二者位置变化共同作用的结果[7],当定子磁链位置不变时,转矩角的变化仅取决于转子磁链位置的变化,此时控制周期内转矩变化情况为
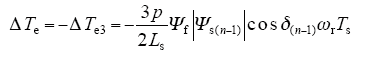
从式(12)可以看出,零矢量作用于电机后电机转矩的变化主要取决于电机转速,当电机低速运行时,ωrTs较小,零矢量引起的转矩角变化较小,电机转矩基本不变,起到保持电机转矩的作用;当电机处于高速运行时,ωrTs较大,此时,零矢量引起的转矩角变化较大,减小电机转矩的作用增强,综合不同转速下零矢量对转矩的控制效果可知,选择零矢量后,电机转矩变化的最大值要明显小于非零矢量所引起的转矩变化的最大值,也即电机稳定运行过程中,根据转矩控制要求将零矢量引入到转矩调节器中有助于降低转矩脉动,提高电机转速的稳定性[8]。
3 转矩调节器设计方法
将零矢量引入转矩调节器后,正弦波永磁同步电机传统DTC方法磁链和转矩调节器如下所示
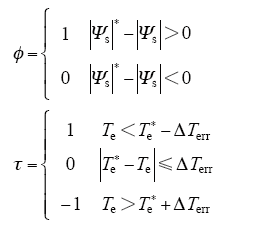
式中,ΔTerr为转矩调节器零矢量作用范围。转矩调节器中,当τ = 1,表示电机转矩小于给定转矩和零矢量作用范围之差,即已超出零矢量的作用范围下限,应选择增加转矩的非零矢量;当τ = -1,表示电机转矩大于给定转矩和零矢量作用范围之和,即已超出零矢量作用范围的上限,应选择减小转矩的非零矢量;当τ = 0,表示转矩给定和电机转矩的误差在零矢量的作用范围内,则选择零矢量作用于电机,以达到减小转矩变化或基本保持电机转矩的目的。当零矢量引入转矩调节器中后,空间电压矢量选择见表1。
表1 含零矢量的选择表
Tab.1
| φ | τ | θ1 | θ2 | θ3 | θ4 | θ5 | θ6 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | u2 | u3 | u4 | u5 | u6 | u1 |
| 0 | u7 | u0 | u7 | u0 | u7 | u0 | |
| -1 | u6 | u1 | u2 | u3 | u4 | u5 | |
| 0 | 1 | u3 | u4 | u5 | u6 | u1 | u2 |
| 0 | u0 | u7 | u0 | u7 | u0 | u7 | |
| -1 | u5 | u6 | u1 | u2 | u3 | u4 |
转矩调节器中引入零矢量的目的是充分利用其对电机转矩的保持作用达到降低转矩脉动的目的,而零矢量作用范围的大小对抑制转矩脉动的效果影响重大,必须仔细研究它的规律。此外,当电机处于起动过程时,如果零矢量作用范围太大,则又会增加电机起动时间,因此,应从转矩脉动得到有效抑制和提高电机起动性能两方面综合考虑零矢量作用范围。
4 仿真分析
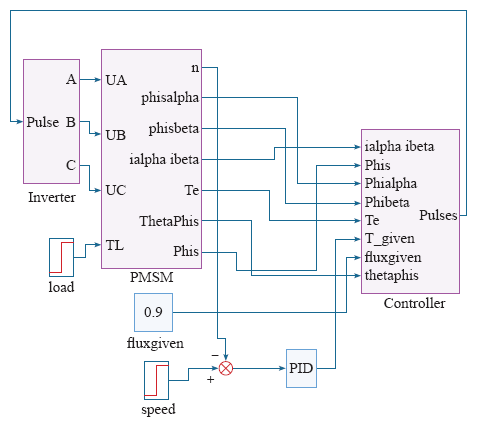
图2
图2
正弦波永磁同步电机直接转矩控制系统仿真模型
Fig.2
Simulation model of sine wave permanent magnet synchronous motor direct torque control system
表2 电机参数
Tab.2
| 电机参数 | 数 值 |
|---|---|
| 额定相电压/V | 257 |
| 额定相电流/A | 1.5 |
| 额定转速/(r/min) | 1 500 |
| 极对数 | 2 |
| 直轴电感/H | 0.113 3 |
| 交轴电感/H | 0.129 5 |
| 定子电阻/Ω | 22.5 |
| 永磁体磁链/Wb | 0.86 |
| 额定定子磁链/Wb | 0.9 |
| 额定转矩/N·m | 5.8 |
仿真中电机给定转速1 500r/min,稳定运行时负载转矩5.8N·m,定子磁链给定0.9Wb,控制周期60μs。首先对从0~1 N·m不同零矢量作用范围下的电机稳态转矩性能进行了仿真分析。将不同零矢量作用范围下转矩脉动情况进行整理,得到表3所示仿真结果。
表3 不同零矢量作用范围下转矩脉动仿真结果
Tab.3
| 零矢量作用范围/ N·m | 仿真转矩脉动/ N·m |
|---|---|
| 0 | 2.98 |
| 0.10 | 2.73 |
| 0.20 | 2.49 |
| 0.30 | 2.37 |
| 0.40 | 1.90 |
| 0.41 | 1.87 |
| 0.42 | 1.85 |
| 0.43 | 1.86 |
| 0.44 | 1.83 |
| 0.45 | 1.80 |
| 0.46 | 1.82 |
| 0.50 | 1.85 |
| 0.60 | 1.81 |
| 0.70 | 1.79 |
| 0.80 | 1.83 |
| 0.90 | 1.81 |
| 1.00 | 1.85 |
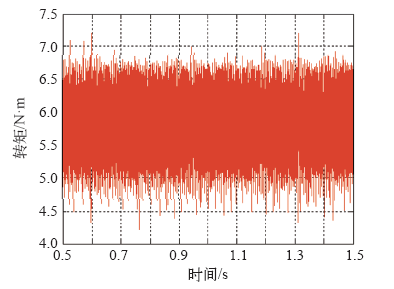
图3
图3
零矢量作用范围0 N · m 转矩仿真波形
Fig.3
Null vector range at 0 N · m torque simulation waveform
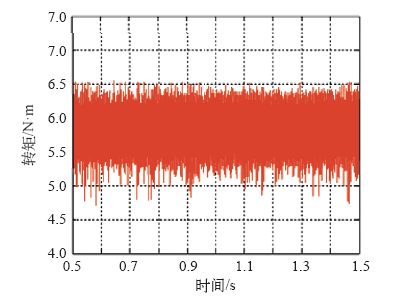
图4
图4
零矢量作用范围0.43 N · m 转矩仿真波形
Fig.4
Null vector range at 0.43 N · m torque simulation waveform
对比两种零矢量作用范围下的转矩波形可知,在作用范围为0 N·m时,转矩脉动为2.98 N·m,当作用范围增加到0.43 N·m时,转矩脉动约为1.86 N·m,相对于额定负载转矩,转矩脉动从原来的51%降低到32%,说明转矩调节器中恰当地引入零矢量后对降低转矩脉动效果非常明显。再结合表3中的仿真结果,仅从降低转矩脉动的角度来看,零矢量作用范围只要不小于0.42 N·m,均能够保证较低的转矩脉动。但从转矩调节器的优化设计角度考虑,稳定运行时较低的转矩脉动只是其中的一个方面,与此同时,还要考虑到零矢量作用范围对电机起动性能的影响,这样才能保证转矩调节器全局设计最优。
对电机在给定转速1 500r/min,空载条件下的起动性能进行仿真分析。这里,根据自动控制理论中对起动时间的定义,规定电机转速从零速开始达到0.9倍给定转速(即1 350r/min)的时间为电机起动时间。对不同零矢量作用范围下的起动情况进行仿真,可得到表4所示的仿真结果。
表4 不同零矢量作用范围下起动时间仿真结果
Tab.4
| 零矢量作用范围/ N·m | 仿真起动时间/ms |
|---|---|
| 0 | 99.7 |
| 0.10 | 96.5 |
| 0.20 | 99.0 |
| 0.30 | 103.0 |
| 0.40 | 108.4 |
| 0.43 | 111.4 |
| 0.45 | 113.9 |
| 0.50 | 119.0 |
| 0.60 | 123.8 |
| 0.70 | 129.0 |
| 0.80 | 130.5 |
| 0.90 | 134.6 |
| 1.00 | 137.8 |
图5
图5
零矢量作用范围0 N · m 转速仿真波形
Fig.5
Null vector range at 0 N · m speed simulation waveform
图6
图6
零矢量作用范围0.43 N · m 转速仿真波形
Fig.6
Null vector range at 0.43 N · m speed simulation waveform
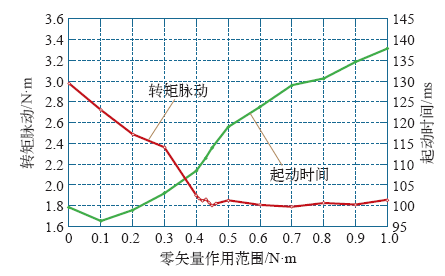
图7
图7
零矢量作用范围对电机稳态性能和起动时间的影响仿真结果
Fig.7
Simulation results of the influence of the zero vector range on the steady state performance and start time
从图7电机转矩脉动和起动时间随零矢量作用范围的变化仿真结果中可知,零矢量作用范围对转矩脉动和起动时间的影响恰好相反。转矩脉动随着作用范围的增加逐渐降低,当作用范围增加到0.43 N·m之后,转矩脉动不再降低;而电机起动时间随着零矢量作用范围的增加先减小,然后当零矢量作用范围大于0.1 N·m之后单调增加,这主要是由于在作用范围为0 N·m时,空间电压矢量对电机转矩控制存在正负不对称性,并且控制周期内转矩减小量大于控制周期内转矩增加量导致平均起动转矩减小,从而增加了电机起动时间。综合零矢量对电机稳态转矩性能和起动性能的影响,零矢量作用范围以0.43 N·m为宜。而0.43 N·m这一转折点意味着什么呢?现用前面分析的转矩变化规律来进一步计算。电机转矩减小时,转矩的最大减小量ΔTermax最大,将电机相关参数代入ΔTermax表达式,可得
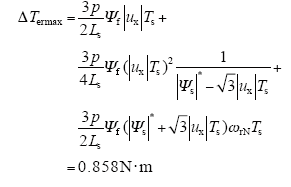
而ΔTermax的一半为0.429N·m,该计算结果仅比由图7确定的0.43N·m小一点点,该转折点的含义初步解释为:使电机转矩在零矢量作用范围上限减小时,它的减小值落入零矢量的作用范围中(即2ΔTerr),保证下一控制周期中不使用使转矩变化很大的非零矢量,而使用保持电机转矩的零矢量,从而显著抑制转矩脉动。
从该仿真中发现,零矢量作用范围0.43N·m为转矩脉动的转折点,通过计算可知,零矢量作用范围0.43N·m正好是该电机控制系统中一个控制周期内转矩变化的最大值的一半。虽然该规律是基于一台具体的电机得到的,但是,通过以上分析,得出如下结论:“零矢量作用范围应为电机控制系统在一个控制周期内转矩变化最大值的一半,以便使电机转矩进入零矢量作用范围时,有一个保持转矩的模式,以减少频繁增减转矩的动作次数”应是适用于一般电机的普遍规律。因此,可以认为,零矢量作用范围的计算应以该电机控制周期内转矩变化最大值为依据,在量化计算时采用下式,即
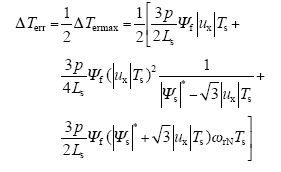
实际上,式(15)即为转矩变化最大值的一半,根据式(15)确定零矢量作用范围,在保证有效抑制转矩脉动的同时能够实现较短的起动时间。
5 结论
本文对数字控制条件下传统DTC中定子磁链幅值、转矩角和电机转矩变化规律进行了详细的定量分析,提出了一种转矩调节器设计方法,对正弦波永磁同步电机传统DTC设计和实现具有借鉴意义。得到如下结论:
(1)传统 DTC方法中转矩的变化和电机极对数、电机电感、转子磁链、空间电压矢量的大小、控制周期的长短、定子磁链的变化以及转矩角的变化有关。
(2)零矢量对电机转矩保持作用的强弱和电机转速有关,在低速条件下,零矢量起到基本保持转矩的作用,高速运行时,电机零矢量作用的时间内转矩是减小的。
(3)零矢量作用范围为电机控制系统在一个控制周期内转矩变化最大值的一半时,转矩脉动最小,起动时间在合理范围内,且可以减少频繁增减转矩的动作次数。
参考文献
In-depth research on direct torque control of permanent magnet synchronous motor
[C].
PMSM调速系统中最大转矩电流比控制方法的研究
[J].
Research on the maximum torque to current ratio control method in PMSM speed regulation system
[J].
A robust sliding mode observer for permanent magnet synchronous motor drives
[C].
Space vector modulated based constant switching frequency direct torque control for PMSM
[J].