电气工程学报, 2018, 13(6): 28-35 doi: 10.11985/2018.06.005

工程技术

基于POP NSGA-Ⅱ的配电网故障恢复重构

周生海1, 尹航2, 顾颖1, 王翀1, 柏峰1

1. 国家电网冀北电力有限公司检修分公司 北京 101100

2. 国家电网冀北电力有限公司承德供电公司 承德 067000

Service Restoration Reconfiguration in Distribution Systems Based on Pareto Optimizing Path NSGA-Ⅱ

Zhou Shenghai1, Yin Hang2, Gu Yin1, Wang Chong1, Bai Feng1

1. State Grid Jibei Electric Power Co.,Ltd. Maintenance Branch Beijing 101100 China

2. State Grid Jibei Electric Power Co.,Ltd. Chengde Power Supply Company Chengde 067000 China

收稿日期: 2018-02-28   网络出版日期: 2018-06-25

Received: 2018-02-28   Online: 2018-06-25

作者简介 About authors

周生海 男 1986年生,工程师,主要从事继电保护专业方面的工作。

尹 航 男 1985年生,工程师,主要从事调度运行专业方面的工作。

摘要

快速的非支配排序遗传算法（NSGA-Ⅱ）可以使每次进化过程中得到的个体分布均匀,具有较好的收敛性和鲁棒性。本文分析了当前遗传算法（GA）的缺陷,将NSGA-Ⅱ应用到配电网的故障恢复重构中,并提出通过一种Pareto寻优路径（POP）控制选择操作的方法,一方面可以扩大搜索面积、避免陷入局部最优;另一方面可以适时地停止进化、减少多余的计算。另外,本文根据模糊集理论确定故障恢复重构的最终解决方案,使NSGA-Ⅱ算法适用于恢复重构问题。算例结果表明,POP NSGA-Ⅱ算法与GA、NSGA-Ⅱ算法相比具有更强的寻优能力,是一种解决配电网故障恢复重构问题的新方法。

关键词： 快速的非支配排序遗传算法 ; 配电网故障恢复重构 ; Pareto寻优路径 ; 模糊集理论 ; POP NSGA-Ⅱ

Abstract

Fast non-dominated sorting genetic algorithm (NSGA-Ⅱ) can obtain uniformly distributed individualities in the every evolutionary process and has more convergence and more excellent robustness. In this paper, the defects of the current genetic algorithm (GA) are analyzed, then NSGA-Ⅱ is applied to service restoration reconfiguration in distribution systems, and a method of controlling the selecting operation by the Pareto optimizing path (POP) is provided. On one hand this method can expand the region of searching and avoid to get into local optimum, on the other it can stop evolving duly and reduce the unnecessary calculation. In addition, the final service restoration reconfiguration method is confirmed based on the fuzzy set theory. The simulation results show that POP NSGA-Ⅱ have more ability of optimizing than GA and NSGA-Ⅱ. It should be a new method for service restoration reconfiguration in distribution systems.

Keywords： NSGA-Ⅱ ; service restoration reconfiguration in distribution systems ; POP ; fuzzy set theory ; POP NSGA-Ⅱ

PDF (2189KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周生海, 尹航, 顾颖, 王翀, 柏峰. 基于POP NSGA-Ⅱ的配电网故障恢复重构. 电气工程学报[J], 2018, 13(6): 28-35 doi:10.11985/2018.06.005

Zhou Shenghai. Service Restoration Reconfiguration in Distribution Systems Based on Pareto Optimizing Path NSGA-Ⅱ. Journal of Electrical Engineering[J], 2018, 13(6): 28-35 doi:10.11985/2018.06.005

1 引言

配电网故障恢复重构的目的是在故障定位和故障隔离以后,通过改变开关的开合状态,在满足电气约束条件的前提下,将非故障失电区域负荷转供到其他正常运行的支路上以恢复对非故障失电区域负荷的供电,从而提高系统的自愈能力和供电可靠性[1,2]。

当前,随着分布式能源的接入和用户供电可靠性要求的提高,配电网的运行方式更加多变,网络的复杂度不断增大,影响因素不断增多,使系统内发生故障的可能性以及故障所影响的区域相应增大,直接影响到用户的供电安全和满意度,同时也损害了供电企业的经济利益。为减少用户和供电企业的损失,故障恢复重构作为智能电网的重要功能成为关注的热点之一。故障恢复重构一方面需采用最少的开关操作次数和线路损耗来恢复最多非故障失电负荷;另一方面,还需满足网络拓扑结构、线路裕量等电气约束。因此,配电网的故障恢复重构是一种高度非线性化、多目标、多约束的优化问题[3,4,5,6]。

目前求解此类问题的方法主要有启发式搜索算法[7,8,9]和智能算法[10,11,12]。启发式搜索算法以禁忌搜索算法（Tabu Search,TS）[13]效果较好,但是为了降低计算量,禁忌长度和禁忌表的集合不宜太大,而禁忌长度太小容易循环搜索,禁忌表太小容易陷入局部最优解。智能算法中以遗传算法（Genetic Algorithm,GA）[14,15,16]应用较多。然而,尽管近几年国内外众多学者对遗传算法进行了大量的改进,产生了克隆遗传算法（Clone Genetic Algorithm,CGA）[17]、免疫遗传算法（Immune Genetic Algorithm,IGA）、模拟退火遗传算法等混合算法,并取得了较好的效果,但是这些算法仍然是通过设置权重因子（Weigh Factor,WF）将多目标问题转化为单目标问题,寻优结果受WF的影响较大,寻优能力不稳定。

快速的非支配排序遗传算法（Fast Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ）[19,20,21]的思想是协调各目标函数之间的关系,对种群进行快速分组,使个体均匀分布在目标空间中,再通过选择、交叉、变异等操作找出使各目标函数均达到最优的解集。该算法通过非支配排序组别和拥挤距离体现个体之间的优劣性,能够较好地避免权重设置对寻优结果带来的影响。本文将NSGA-Ⅱ应用于配电网的故障恢复重构,并对选择操作进行了改进,提出一种Pareto寻优路径（Pareto Optimizing Path,POP）,一方面有效地加快了收敛速度,扩大了搜索面积,避免了陷入局部最优;另一方面,可以准确地判断进化进度,进而适时地停止进化。最后通过算例表明了这种方法的可行性与良好的寻优效果,为解决配电网故障恢复重构问题提供了一种新的思路。

2 配电网故障恢复重构的数学模型

恢复重构需要考虑的因素包括恢复供电量、开关操作、线路损耗,停电时间、电压分布等目标函数和线路容量、网络拓扑,支路电流和节点电压等约束条件。为方便描述,本文主要考虑部分目标和约束条件。

2.1 目标函数

（1）尽量恢复更多非故障失电负荷的供电,即

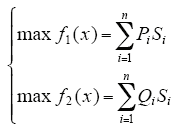
（2）尽量减少开关操作次数,即

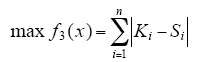
（3）尽量减少线路损耗,即

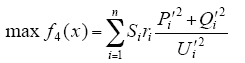
式中：x为当前网络的状态,与参与重构的所有支路闭合有关;Si为第i个支路的闭合情况,“0”为打开,“1”为闭合;Pi和Qi为与第i个支路相连节点的额定有功功率和无功功率;Ki为第i个支路最初的闭合状态;Pi′、Qi′和Ui′分别为支路i上的有功功率、无功功率以及末端的节点电压;ri为支路i的电阻;n为参与重构的所有支路总数。

2.2 约束条件

（1）线路容量约束,即

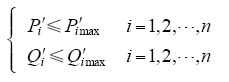
（2）配电网辐射网络运行约束,即无“回路”。

（3）节点电压约束,即

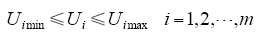
式中,P′imax和Q′imax为支路i允许流过的最大有功功率、无功功率;Ui、Uimax和Uimin为节点i的电压及电压上下限;m为节点总数。

3 NSGA-Ⅱ在恢复重构中的应用

3.1 快速的非支配排序遗传算法

与传统GA相比,NSGA-Ⅱ算法同样需要通过选择、交叉、变异等操作产生新一代个体;不同的是两类算法处理多目标问题的方式,GA算法使用权重因子将多目标转化为单目标进而得到适应度函数值,并以此体现个体的优劣性,而NSGA-Ⅱ算法通过非支配排序分类程序,将多目标简化至一个适应度函数,并且定义了拥挤距离估计某个体周围的解密度,判断个体的差异,从而避免了权重对寻优结果产生的影响。

NSGA-Ⅱ需要对非支配排序、拥挤距离进行计算,其具体实现原理和方法在文献[20]中有所介绍,本文不再赘述。

3.2 基于NSGA-Ⅱ的故障恢复重构的算法流程

NSGA-Ⅱ算法已经在一些实际工程中得到了广泛的应用。文献[21,22,23]分别提出将NSGA-Ⅱ算法应用于含分布式电源的配网重构、无功优化和电网规划等问题。本文尝试将NSGA-Ⅱ算法应用于配电网的故障恢复重构,其具体实现步骤如下：

（1）编码。本文采取二进制方式,将参与重构的所有开关进行编号,“0”和“1”分别代表开关当前状态为“打开”和“闭合”。

（2）产生随机初始种群。随机产生一个大小为N的初始种群P0。

（3）目标函数值计算。通过潮流计算获得每个染色体的目标函数值。

（4）非支配排序和虚拟适应度计算。

（5）选择运算。选择操作采用精英策略,即保留父代中的优良个体直接进入子代,它是遗传算法以概率1收敛的必要条件,目的是使进化朝着Pareto最优解的方向进行,并且避免染色体在局部拥挤。因此,选择算子要保证种群中优良的个体以最大的概率生存,从而提高全局最优和计算效率。

（6）交叉和变异。交叉可以保留父代染色体中优良的基因,变异可以避免种群个体的性状过于单一,两者相互配合可使遗传算法具有良好的搜索能力。正态变异算子是基于正态分布的变异操作。

（7）判断终止条件。判断是否达到预设的最大迭代次数或者寻找到最优方案,如果是终止迭代,则输出计算结果,否则,应返回步骤（3）继续迭代。

4 基于Pareto寻优路径的NSGA-Ⅱ

4.1 Pareto寻优路径

Pareto寻优路径（POP）主要包含两方面信息：Pareto寻优方向（Pareto Optimizing Tend,T）和Pareto最优解集F1中染色体的数目（Chromosome Number,CNum）。

（1）Pareto寻优方向（T）。当进化过程进行到第n次时,由精英策略可以得到Pareto最优解集F1,它体现了当前进化的最高水平。那么,定义第n + 1次Pareto寻优方向值Tn+1为

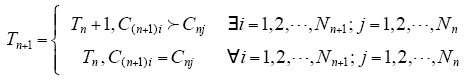
式中,C(n+1)i为进化到第n + 1次时F1中第i个染色体;Cnj为进化到第n次时F1中第j个染色体; 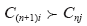为染色体Cnj被C(n+1)i所支配;Tn为第n次寻优方向值,n = 1时,T1 = 0。通过对比连续两次进化中Pareto最优解集F1的变化情况,得到Pareto寻优方向T。T可以如实地反映进化的方向,跟踪进化的轨迹。

（2）F1中染色体的数目（CNum）。由于NSGA-Ⅱ算法所得到最优解的个数未知,CNum的变化同样可以反映进化情况。

由式（6）和CNum的变化可以导出POP的计算式为

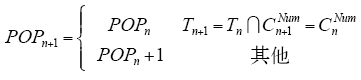
其中,CnNum为进化到第n次时F1中染色体的数目。

T和CNum相互配合可以体现F1中染色体的变化。当F1中仅增加了目标值相同的染色体而T不变,或者CNum不变而F1中的染色体已经被更优的个体所取代,只要父代F1有更新动作,POP就能如实反映出来,即在进化中,只要子代种群找到更优的或者与父代最优个体目标值相同但基因不同的新个体,POP均能体现。

4.2 虚拟适应度

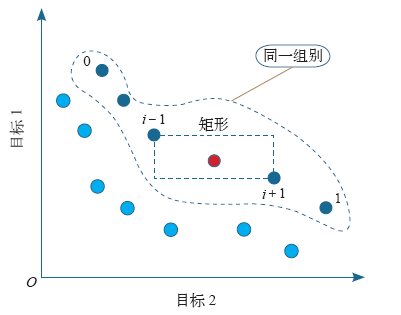
虚拟适应度是目标空间中的每一点（个体）与同层相邻两点之间的局部拥挤距离。以F(x) = (f1(x), f2(x), …, fk(x))为例,令k = 2,则图1目标空间中第i点的拥挤距离等于该点在同一组别中相邻的点i - 1和i + 1在目标1轴和目标2轴的距离之和,即为点i - 1和点i + 1组成的矩形周长的1/2。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   局部拥挤距离示例图

Fig.1   Crowding distance in local space


4.3 POP 选择算子

根据Pareto寻优路径,选择规模S的大小定义为

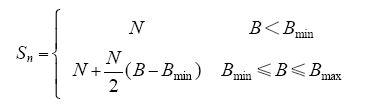
式中,N为初始种群大小;B、Bmax、Bmin分别为POP连续不发生变化的次数及上下限。

由式（8）可知,当连续Bmin进化没有进展时,则选择规模S将随着B的增大不断递增,搜索面积和搜索能力不断提高。当B = Bmax时,进化依然没有进展,则程序停止,当前F1为最优解集。

投入POP选择算子使算法增加的计算量ΔM为

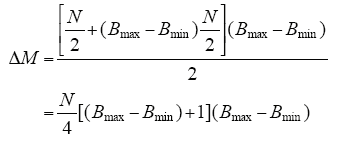
由式（9）可知,在寻优没有进展的情况下,适当地增加选择规模的大小,可增加全局和局部搜索面积,进而减少局部收敛的可能性,避免出现早熟的现象;同时,计算最大增加量相当于多进化(Bmax - Bmin + 1)(Bmax - Bmin)/4次。因此,只要合理地控制Bmax、Bmin,POP选择算子并不会增加计算负担。

4.4 相似度交叉算子

相似度交叉算子（Semblance Crosser,SC）需要对比两个父代染色体之间的基因相差值SC。当SC = 0或者SC = 1时,采用SBX随机产生的子代染色体总与父代相同,这样不利于种群的进化,相似度交叉算子采取基因重组策略,即父代染色体的所有基因随机进行排列组合产生子代;当SC>1时,见表1,若随机交叉点在1~4、8~9的位置,则交换交叉点两侧的基因产生的子代同样与父代相同。因此,相似度交叉算子随机选取基因5、6、7作为交叉点。

表1   相似度交叉算子示意图

Tab.1  Chart of semblance crosser

基因编号123456789
父代1100110101
父代2100011001

新窗口打开| 下载CSV


相似度交叉算子可提高种群的进化效率,避免无效进化,进而加快收敛速度。

4.5 确定最优方案

在实际应用中,恢复重构问题最终需要的方案只有一个,因此决策者需要根据实际情况在F1中确定最优解。本文采取模糊集理论确定最优方案[24]。F1中个体的满意度可表示为

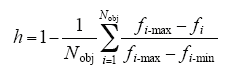
式中,i∈{1,2,…,Nobj},Nobj为目标函数的个数;fi为目标函数;fi-max和fi-min为F1中第i个目标函数的最大值和最小值。

最后将具有最大h值的个体作为最优方案。

4.6 基于POP NSGA-Ⅱ的恢复重构流程图

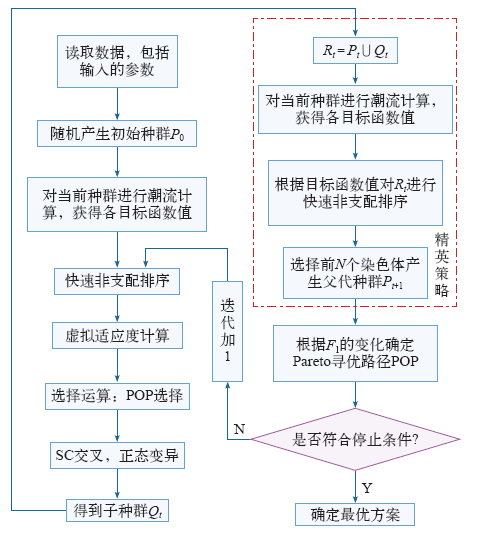
由NSGA-Ⅱ算法流程和Pareto寻优路径的提出,可得到基于POP NSGA-Ⅱ算法的配电网故障恢复重构的流程图如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   算法流程图

Fig.2   Flow chart of calculation


5 算例验证和分析

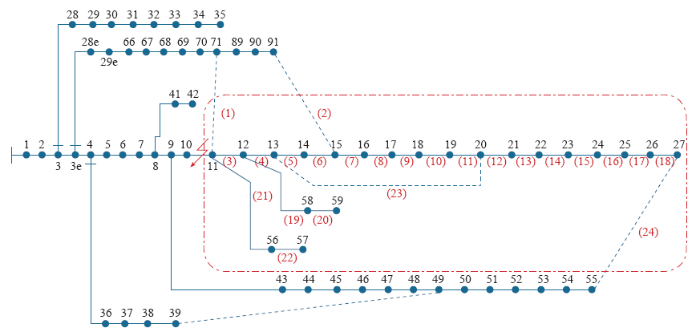
本算例是PG&E 69节点单电源的配网系统,其原始网络结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   PG&E 69节点配网系统

Fig.3   PG&E 69 bus system


图3中实线3~22为运行支路,虚线1、2、23、24为联络支路。初始状态时,运行支路全部闭合,联络支路全部打开,网络参数见文献[25]。假设节点10-11发生故障,故障切除后,故障点下游区域的节点11~27、56~59都会失去供电。为验证算法,以恢复最大供电负荷有功功率f1、无功功率f2和最小开关操作次数f3为目标函数,以重构后保持辐射状网络、满足联络支路容量为约束条件,分别采用禁忌克隆遗传算法（Tabu Search Clonal Genetic Algorithm,TSCGA）、传统NSGA-Ⅱ算法和本文算法对算例进行配电网故障恢复重构的仿真计算。各算法的运行参数设置如下：初始种群规模为100,最大迭代次数为200,交叉概率为0.9,变异概率为0.1,POP选择算子投入时Pareto寻优路径连续不变最小次数Bmin = 5,最大次数即停止条件Bmax = 10。联络支路1、2、24可提供的最大有功功率分别为350、300、250kW,无功功率分别为250、200、150kvar。由于算法均采用了随机操作,为真实体现算法的寻优效果,每种算法连续运行100次,所得结果为平均值。另外,为分析权重对GA算法的影响,在TSCGA算法中将考虑所有步长为0.1的权重系数W组合,因篇幅所限,只给出几种寻优结果,见表2。

表2   TSCGA算法的计算结果

Tab.2  The computing result of TSCGA

权重分配0.8/0.1/0.10.7/0.2/0.10.6/0.2/0.200.5/0.2/0.3
f1/kW681.493 9668.387 6630.834 2586.741 2
f2/kvar431.234 4422.587 4411.685 3388.286 4
f3/次6.579.338.758.15
时间/s6.587 86.674 86.536 66.672 7
稳定性(%)81766965

新窗口打开| 下载CSV


表2中稳定性为100次计算结果中相同最优解个数所占的比例。从表2可以看出,由于TSCGA算法的寻优结果偏重于W分配较高的目标值,使W分配较低的目标值对遗传操作的影响极小,所以不能保证所有目标值都达到最优;同时,稳定性受W的影响较大,即每次寻优结果存在较高的差异。

三种算法的计算结果见表3。表3中,POP NSGA-Ⅱ与NSGA-Ⅱ算法相比,POP NSGA-Ⅱ算法增大了F1的规模,为操作者提供了更多的选择;另一方面,POP NSGA-Ⅱ算法通过提高进化效率,减小了迭代次数、缩短了进化时间、提高了寻优结果的稳定性和质量。

表3   三种算法的计算结果

Tab.3  The computing results of three algorithms

算法NSGA-ⅡPOP NSGA-ⅡTSCGA (0.8/0.1/0.1)
f1 /kW695.8701.5681.493 9
f2 /kvar460.1469.6431.234 4
f3 /次6.9946.3699.576
时间/s6.753 46.286 46.287 8
迭代次数68.66859.48278.659
F1中个体数8.15911.615-
稳定性(%)919981

新窗口打开| 下载CSV


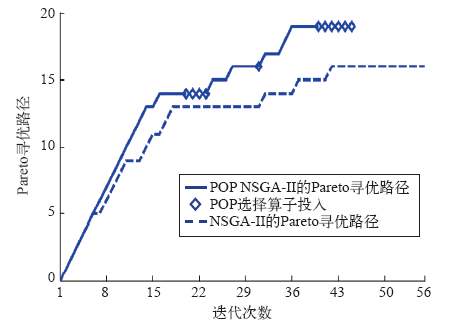
图4为采用相同初始种群和随机操作时,POP NSGA-Ⅱ算法和NSGA-Ⅱ算法单次计算的Pareto寻优路径。在进化初期,由于本文算法采用相似度交叉算子,所以其进化不断向Pareto最优解方向进行,进化效率较高;在迭代次数达到一定程度以后,两种算法均进入了进化缓慢阶段,由于POP选择算子的投入,POP NSGA-Ⅱ算法通过适时增加种群规模、交叉和变异操作,进而产生更多的新个体、加大搜索面积,及时跳出局部最优,有效地避免了早熟。在此方法中,POP选择算子共投入使用11次,由式（9）得到增加的计算量相当于11次遗传操作;当迭代次数达到45次时,由Pareto寻优路径判定程序停止。而传统的NSGA-Ⅱ算法两次陷入局部最优,在连续15次的进化中,没有任何进展。表4为两种算法本次的计算结果。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   Pareto寻优路径

Fig.4   Pareto optimizing path


表4   两种算法的单次计算结果

Tab.4  The computing results of two algorithms once

算法NSGA-ⅡPOP NSGA-Ⅱ
F1中最优解个数914
最终方案动作开关1, 2, 4, 5, 15, 21, 241, 2, 4, 12, 21, 24
恢复重构效果f1 = 695.8kWf1 = 703.8kW
f2 = 478.6kvarf2 = 484.1kvar
f3 = 7f3 = 6

新窗口打开| 下载CSV


6 结论

本文将NSGA-Ⅱ算法应用于配电网的故障恢复重构问题。通过Pareto寻优路径控制选择操作,一方面在进化受阻、缓慢的情况下,加大搜索面积,减小陷入局部最优的可能性;另一方面,适时地停止进化,避免多余的计算。同时,应用模糊集理论在最优解集F1中确定输出方案,使NSGA-Ⅱ算法完全适用于故障恢复重构问题。PG&E 69节点的算例说明POP NSGA-Ⅱ算法的恢复重构效果和F1中最优解个数均优于传统的NSGA-Ⅱ算法。

参考文献

张浩, 和敬涵, 尹航 , 等.

电网孤岛重构的云计算策略

[J]. 中国电机工程学报, 2011,31(34):77-84.

URL     [本文引用: 1]

提出了一种基于云计算思想的电网恢复重构方法，利用网络中大量的分布式计算资源加速求取孤岛间网络恢复重构的最优解。利用电力系统分层分布式体系结构将含有多个微网的复杂配电网络视为不同的子云计算区，每个子云计算区根据自身情况将重构的服务请求分解为多个可独立处理的计算块并提交分布的计算节点进行并行处理和结果取优。相关联子云计算区之间可通信以协调不同区域间的负荷转供，最终实现故障恢复重构的目标。算例分析结果验证了该方法的有效性。

Zhang Hao, He Jinghan, Yin Hang , et al.

Power grid islands service restoration based on cloud computing

[J]. Proceedings of the CSEE, 2011,31(34):77-84.

URL     [本文引用: 1]

提出了一种基于云计算思想的电网恢复重构方法，利用网络中大量的分布式计算资源加速求取孤岛间网络恢复重构的最优解。利用电力系统分层分布式体系结构将含有多个微网的复杂配电网络视为不同的子云计算区，每个子云计算区根据自身情况将重构的服务请求分解为多个可独立处理的计算块并提交分布的计算节点进行并行处理和结果取优。相关联子云计算区之间可通信以协调不同区域间的负荷转供，最终实现故障恢复重构的目标。算例分析结果验证了该方法的有效性。

张浩, 和敬涵, 薄志谦 , 等.

基于动态规划算法的故障恢复重构

[J]. 电工技术学报, 2011,26(12):162-167.

URL     [本文引用: 1]

A new method is presented to restore the power system based on dynamic programming (DP). After isolated a fault, the out-of service area, which is constructed of load nodes could be divided into several groups, each has one contact branch used for load distribution. These groups sharply decrease the number of calculation loops. According to the different restore orders of the load nodes, operation sequences are produced, which turn the restore problem into a node-string choice. Based on a DP method, operation sequences are used to build a multiple-stage decision model, each contact branch is calculated as one stage, the algorithm is designed to transfer and restore the largest load capacity by optimal choice of the node-string. In each stage, the calculation process records the optimal state and lists the decision variable. The optimal result is obtained at the final stage. This method can be used to power service reconfiguration, when the power capacity is not enough to support all of the out-of service nodes, reducing the time of outage and improve the reliability of system. The proposed method is validated by simulation methods.

Zhang Hao, He Jinghan, Bo Zhiqian , et al.

Service restoration based on dynamic programming

[J]. Transactions of China Electrotechnical Society, 2011,26(12):162-167.

URL     [本文引用: 1]

A new method is presented to restore the power system based on dynamic programming (DP). After isolated a fault, the out-of service area, which is constructed of load nodes could be divided into several groups, each has one contact branch used for load distribution. These groups sharply decrease the number of calculation loops. According to the different restore orders of the load nodes, operation sequences are produced, which turn the restore problem into a node-string choice. Based on a DP method, operation sequences are used to build a multiple-stage decision model, each contact branch is calculated as one stage, the algorithm is designed to transfer and restore the largest load capacity by optimal choice of the node-string. In each stage, the calculation process records the optimal state and lists the decision variable. The optimal result is obtained at the final stage. This method can be used to power service reconfiguration, when the power capacity is not enough to support all of the out-of service nodes, reducing the time of outage and improve the reliability of system. The proposed method is validated by simulation methods.

Lim S I, Lee S J, Choi M S , et al.

Service restoration methodology for multiple fault case in distribution systems

[J]. IEEE Transactions on Power Systems, 2006,21(4):1638-1644.

DOI:10.1109/TPWRS.2006.879275      URL     [本文引用: 1]

Manjunath K, Mohan M R .

A new hybrid multi-objective quick service restoration technique for electric power distribution systems

[J]. International Journal of Electrical Power & Energy Systems, 2007,29:51-64.

DOI:10.1016/j.ijepes.2005.12.012      URL     [本文引用: 1]

Huang C M .

Multi-objective service restoration of distribution systems using fuzzy cause-effect networks

[J]. IEEE Transactions on Power Systems, 2003,18(2):867-874.

DOI:10.1109/TPWRS.2003.811003      URL     [本文引用: 1]

陈竟成, 徐德超, 于尔铿 , 等.

配电网故障恢复系统

[J]. 电力系统自动化, 2000,24(4):46-51.

[本文引用: 1]

Chen Jingcheng, Xu Dechao, Yu Erkeng , et al.

Distribution fault detection, isolation and restoration system in a distribution management system

[J]. Automation of Electric Power Systems, 2000,24(4):46-51.

[本文引用: 1]

Raju G K V, Bijwe P R .

An efficient algorithm for minimum loss reconfiguration of distribution system based on sensitivity and heuristics

[J]. IEEE Transactions on Power Systems, 2008,23(3):1401-1407.

DOI:10.1109/TPWRS.2008.926702      URL     [本文引用: 1]

Shirmohammadi D, Hong H W .

Reconfiguration of electric distribution networks for resistive line losses reduction

[J]. IEEE Transactions on Power Delivery, 1989,4(2):1492-1498.

DOI:10.1109/61.25637      URL     [本文引用: 1]

陈根军, 李继洸, 唐国庆 .

基于Tabu搜索的配电网络重构算法

[J]. 中国电机工程学报, 2002,22(10):28-33.

[本文引用: 1]

Chen Genjun, Li Jiguang, Tang Guoqing .

A tabu search approach to distribution network reconfiguration for loss reduction

[J]. Proceedings of the CSEE, 2002,22(10):28-33.

[本文引用: 1]

徐廷炜, 贾嵘 .

基于人工免疫思想的蚁群算法(AIACS)在配电网重构中的应用

[J]. 电力系统保护与控制, 2010,38(18):89-93.

DOI:10.7667/j.issn.1674-3415.2010.18.018      URL     [本文引用: 1]

Xu Yanwei, Jia Rong .

Application of artificial immune theory-based ant colony system (AIACS) in reconfiguration of distribution networks

[J]. Power System Protection and Control, 2010,38(18):89-93.

DOI:10.7667/j.issn.1674-3415.2010.18.018      URL     [本文引用: 1]

于永哲, 黄家栋 .

基于改进模拟植物生长法的配电网络重构

[J]. 电力系统保护与控制, 2010,38(2):40-43.

DOI:10.7667/j.issn.1674-3415.2010.02.009      URL     [本文引用: 1]

Yu Yongzhe, Huang Jiadong .

Reconfiguration of distribution network based on improved plant growth simulation algorithm

[J]. Power System Protection and Control, 2010,38(2):40-43.

DOI:10.7667/j.issn.1674-3415.2010.02.009      URL     [本文引用: 1]

李振坤, 陈星莺, 余昆 , 等.

配电网重构的混合粒子群算法

[J]. 中国电机工程学报, 2008,28(31):35-41.

URL     [本文引用: 1]

通过将二进制粒子群算法和离散粒子群算法相结合，提出一种混合粒子群算法，求解配电网重构问题。在求解过程中，通过对配网支路进行分组，简化了网络，编码时每一支路组用1维表示，不仅显著降低了维数，缩短了编码长度，更有效降低了无效粒子的产生概率。在搜索过程中，根据该文总结的配电网重构的必要条件，有规律地将粒子进化，进一步提高了搜索效率。在优化过程中将每一次迭代由2步完成：第1步根据二进制粒子群算法中的sigmoid()函数值，利用轮盘赌的方法优化选择断开的支路组；第2步利用提出的离散粒子群算法优化选择在第1步中被选中断开的支路组的内部断开支路。最后对一个典型的69节点算例和一个实际算例进行仿真，结果显示，该方法不仅能快速收敛，而且稳定性好。

Li Zhenkun, Chen Xingying, Yu Kun , et al.

Hybrid particle swarm optimization for distribution network reconfiguration

[J]. Proceedings of the CSEE, 2008,28(31):35-41.

URL     [本文引用: 1]

通过将二进制粒子群算法和离散粒子群算法相结合，提出一种混合粒子群算法，求解配电网重构问题。在求解过程中，通过对配网支路进行分组，简化了网络，编码时每一支路组用1维表示，不仅显著降低了维数，缩短了编码长度，更有效降低了无效粒子的产生概率。在搜索过程中，根据该文总结的配电网重构的必要条件，有规律地将粒子进化，进一步提高了搜索效率。在优化过程中将每一次迭代由2步完成：第1步根据二进制粒子群算法中的sigmoid()函数值，利用轮盘赌的方法优化选择断开的支路组；第2步利用提出的离散粒子群算法优化选择在第1步中被选中断开的支路组的内部断开支路。最后对一个典型的69节点算例和一个实际算例进行仿真，结果显示，该方法不仅能快速收敛，而且稳定性好。

黄弦超, 舒隽, 张粒子 , 等.

免疫禁忌混合智能优化算法在配电网检修优化中的应用

[J]. 中国电机工程学报, 2004,24(11):96-100.

[本文引用: 1]

Huang Xianchao, Shu Jun, Zhang Lizi , et al.

Distribution maintenance scheduling using an intelligent optimal approach mixed with immune algorithm and tabu search

[J]. Proceedings of the CSEE, 2004,24(11):96-100.

[本文引用: 1]

唐斌, 罗安, 王击 .

改进遗传算法的编码策略及其在配电网重构中的应用

[J]. 继电器, 2004,32(13):35-39.

[本文引用: 1]

Tang Bin, Luo An, Wang Ji .

The improved encoding strategy of genetic algorithm and its application in reconfiguration of distribution networks

[J]. Relay, 2004,32(13):35-39.

[本文引用: 1]

邹必昌, 龚庆武, 李勋 .

基于负荷平衡的配电网重构遗传算法研究

[J]. 电力系统保护与控制, 2011,39(6):80-93.

DOI:10.7667/j.issn.1674-3415.2011.06.016      URL     [本文引用: 1]

Zou Bichang, Gong Qingwu, Li Xun .

Research on network reconfiguration GA in distribution system based on load balancing

[J]. Power System Protection and Control, 2011,39(6):80-93.

DOI:10.7667/j.issn.1674-3415.2011.06.016      URL     [本文引用: 1]

王韶, 马晶晶, 周鑫 , 等.

配电网重构的蜜蜂型遗传算法

[J]. 电力系统保护与控制, 2010,38(16):62-67.

DOI:10.7667/j.issn.1674-3415.2010.16.012      URL     [本文引用: 1]

Wang Shao, Ma Jingjing, Zhou Xin , et al.

Bee evolution genetic algorithm for distribution network reconfiguration

[J]. Power System Protection and control, 2010,38(16):62-67.

DOI:10.7667/j.issn.1674-3415.2010.16.012      URL     [本文引用: 1]

周辉, 王击, 罗安 , 等.

克隆遗传算法与模拟退火算法相结合的配电网重构

[J]. 继电器, 2007,35(7):41-45.

[本文引用: 1]

Zhou Hui, Wang Ji, Luo An , et al.

Distribution network reconstruction based on the combination of CGA and SA

[J]. Relay, 2007,35(7):41-45.

[本文引用: 1]

王林川, 梁栋, 于冬皓 , 等.

基于遗传和禁忌搜索混合算法的配电网重构

[J]. 电力系统保护与控制, 2009,37(6):27-31.

DOI:10.7667/j.issn.1674-3415.2009.06.006      URL    

Wang Linchuan, Liang Dong, Yu Donghao , et al.

Distribution network reconfiguration based on genetic/tabu search hybrid algorithm

[J]. Power System Protection and Control, 2009,37(6):27-31.

DOI:10.7667/j.issn.1674-3415.2009.06.006      URL    

Sbalzarini I F, Muller S, Koumoutsakos P.

Multiobjective optimization using evolutionary algorithms

[C]. Center for Turbulence Research, Proceedings of the Summer Program, 2000: 63-74.

[本文引用: 1]

Srinivas N, Deb K .

Multiobjective function optimization using nondominated sorting genetic algorithms

[J]. Evol. Comput., 1995,2(3):221-248.

DOI:10.1162/evco.1994.2.3.221      URL     [本文引用: 2]

Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal , et al.

A fast and elitist multiobjective genetic algorithm: NSGA-II

[J]. IEEE Transactions on Evolutionary Computation, 2002,6(2):182-197.

DOI:10.1109/4235.996017      URL     [本文引用: 2]

黄弦超 .

含分布式电源的配电网故障恢复模型

[J]. 电力系统保护与控制, 2011,39(19):52-57.

DOI:10.7667/j.issn.1674-3415.2011.19.008      URL     [本文引用: 1]

Huang Xianchao .

Model of service restoration of distribution systems with distributed generation

[J]. Power System Protection and Control, 2011,39(19):52-57.

DOI:10.7667/j.issn.1674-3415.2011.19.008      URL     [本文引用: 1]

冯士刚, 艾芊 .

带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用

[J]. 电工技术学报, 2007,22(12):146-151.

[本文引用: 1]

Feng Shigang, Ai Qian .

Application of fast and elitist non-dominated sorting generic algorithm in multi-objective reactive power optimization

[J]. Transactions of China Electrotechnical Society, 2007,22(12):146-151.

[本文引用: 1]

王秀丽, 李淑慧, 陈皓勇 , 等.

基于非支配遗传算法及协同进化算法的多目标多区域电网规划

[J]. 中国电机工程学报, 2006,26(16):11-15.

[本文引用: 1]

Wang Xiuli, Li Shuhui, Chen Haoyong , et al.

Multi-objective and multi-district transmission planning based on NSGA-II and cooperative co-evolutionary algorithm

[J]. Proceedings of the CSEE, 2006,26(16):11-15.

[本文引用: 1]

陈水利, 李敬功, 王向公 . 模糊集理论及其应用[M]. 北京: 科学出版社, 2005.

[本文引用: 1]

刘健, 毕鹏翔, 董海鹏 . 复杂配电网简化分析与优化[M]. 北京: 中国电力出版社, 2002.

/

〈 〉