1 引言
目前,检测电压暂降信号的方法主要有时域法和坐标变换法。时域法通过求取差变信号检测电压暂降发生的时刻及持续时间;坐标变换法包括短时傅里叶变换、dq坐标变换以及小波变换等[5,6,7,8]。其中,小波变换具有良好的暂态信号分析能力,能够准确识别电压突变点的特征量,受到研究人员的广泛关注[9,10,11]。文献[12]采用现场可编程序阵列(Field-Programmable Gate Array,FPGA)实现了小波变换算法对电压暂降的实时检测,时间延迟达到1ms,满足工程应用的实时性要求。然而,滤波和去噪是确保电压暂降检测实时和精确的关键。在实际应用中,检测信号中存在的噪声和谐波干扰会影响小波变换的检测分析能力,导致误差增大甚至造成误判。文献[13]提出了采用设置阈值的方法对小波高频系数进行量化以消除噪声影响,而阈值的选取在实际应用中往往难以确定。文献[14]提出了运用多尺度小波分解的方法,充分考虑利用高频和次高频分量来抑制噪声幅值,但对于较大噪声幅值以及存在谐波的情况下容易发生误判。文献[15]提出了利用加权最小二乘估计算法和重置协方差来快速判断电压暂降,但谐波分量的频繁变化将会导致阈值不断重置。文献[16]提出了利用双小波进行粗估计和精确定位起止时刻的方法,以排除噪声干扰,但高频次谐波存在影响模极大值的奇异点,降低了小波分析的检测能力。
本文首先研究了噪声和谐波在小波各尺度上的传播特性,提出了双小波检测思想,即在大尺度下分析提取信号基波成分,在小尺度下分析电压突变信息。在此基础上,本文研究了消失矩阶数对基波信息提取精度和暂降信息定位的影响,选取合理的小波函数,确定双小波检测方案,并通过Matlab/Simulink仿真验证了该方法的可行性。
2 小波分析方法
2.1 小波变换
小波变换的窗口大小可根据信号频率进行调整,其本质思想是将信号表示为以小波函数和派生出的尺度函数为基的代数和。对于任意信号f(t)∈L2(R)和小波函数Ψ(t),其连续小波变换可表示为
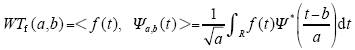
式中,<f(t),Ψa,b(t)>表示f(t)与Ψa,b(t)的内积;Ψ*为小波函数Ψ的共轭函数;a为尺度因子,表征信号在频域的伸缩;b为平移因子,表征信号在时域的平移。
2.2 多分辨分析与滤波
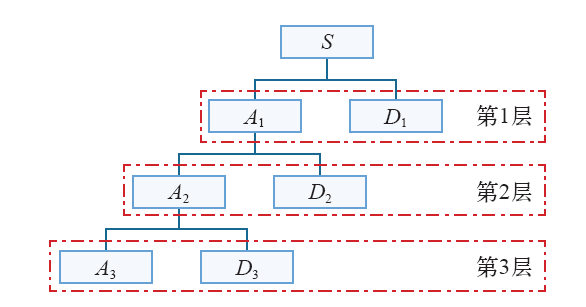
小波函数的时频窗口中心和半径随尺度因子的变化而变化。通常,将尺度因子进行离散化(a = 2j,j为整数),实现频域的逐层下行二分。对信号进行小波变换相当于将信号分解到不同频段中,小波系数表征各频段信号的分量信息。各频段的小波系数可以经过逆变换进行重构以还原信号分量,进而获得信号的基波或谐波信息。图1为尺度为3(j = 3)的小波分解示意图。信号S经小波变换后表示为S = A1 + D1 + D2 + D3,A1、A2、A3表征信号的低频轮廓,对应频段0~fs/4、0~fs/8、0~fs/16,其中fs为采样频率,D1、D2、D3表征信号的高频细节,对应频段fs/4~fs/2、fs/8~fs/4、fs/16~fs/8,对于信号的高频分量,采用小尺度短视窗进行分析,对于信号低频分量,采用大尺度宽视窗进行分析。通过合理地设置采样频率与分解尺度,可使信号的基波与谐波有效分离,基波信息存在于最低频段中,谐波信息分布于各高频频段中。
图1
2.3 奇异性检测与暂降定位
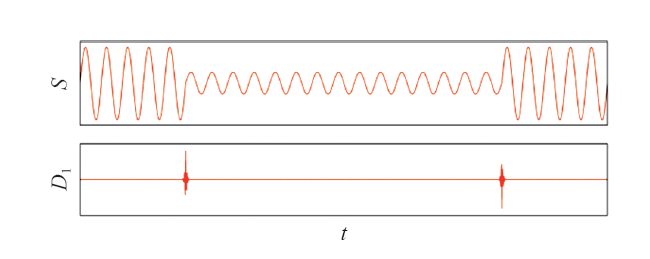
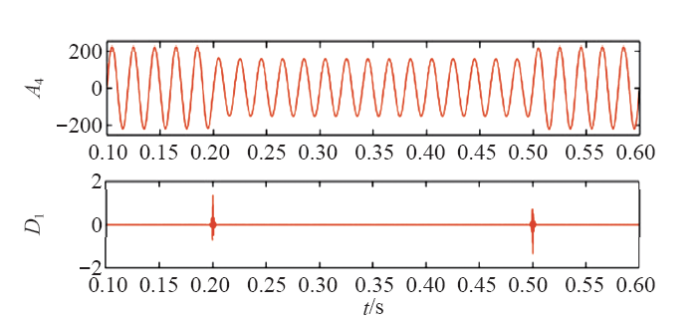
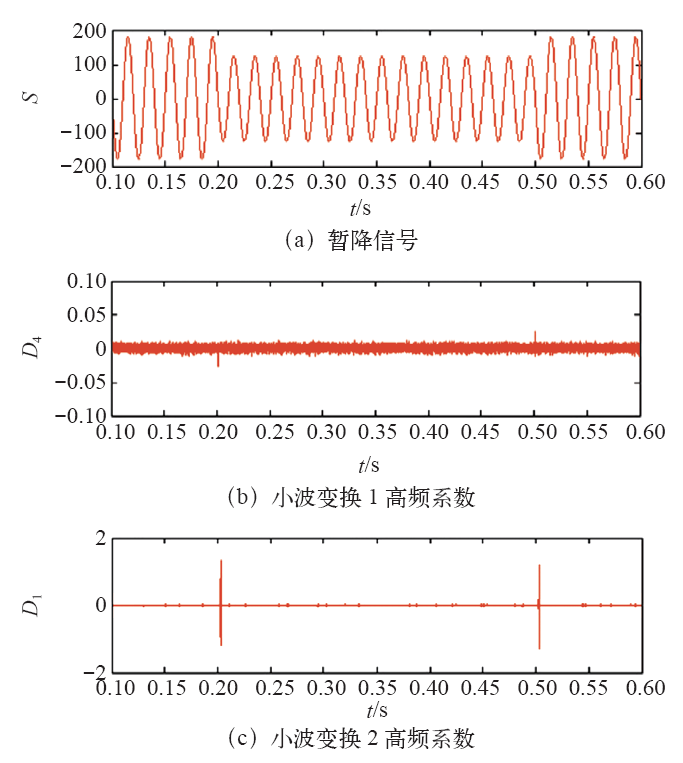
电压暂降属于奇异信号的一种,相当于在信号的奇异点处叠加脉冲函数或阶跃函数。Mallat证明了信号的局部奇异性与小波变换模极大值密切相关。信号的奇异点与小波系数的模极大值点在时域上存在对应关系,并从一个尺度传播到另一个尺度,同时在各尺度上均保持极大值,通过检测小波分解高频段的模极大值点,进而确定原始信号中暂降发生的起止时刻。图2为电压暂降信号的单尺度分解结果,D1为高频段的重构信号分量。从高频分量D1中可以明显识别出模极大值点,分别对应电压暂降的起止时刻。
图2
3 双小波暂降检测
小波分析方法通过检测最高频段D1或次高频段D2的模极大值来实现电压暂降定位。在实际应用中,由于噪声和谐波的存在,往往会导致检测性能下降甚至失效。
3.1 传播特性
暂降信号、噪声与谐波在小波各尺度的传播特性各不相同。以220V含有暂降的工频信号为例,加入3次谐波、13次谐波以及白噪声干扰,分别研究暂降、噪声与谐波在小波各尺度的传播特性,信号特征及分析条件见下表。
表1 信号特征参数及仿真分析条件(没有1)
Tab1
| 参数 | 数值 |
|---|---|
| 电压幅值/频率 | 220V/50Hz |
| 谐波 | 3、13次谐波 |
| 白噪声 | 最大幅值为1V |
| 电压暂降(%) | 60 |
| 暂降起止时刻/s | 0.2~0.5 |
| 采样频率/Hz | 3 200 |
| 小波函数 | db10 |
| 分解尺度 | 4 |
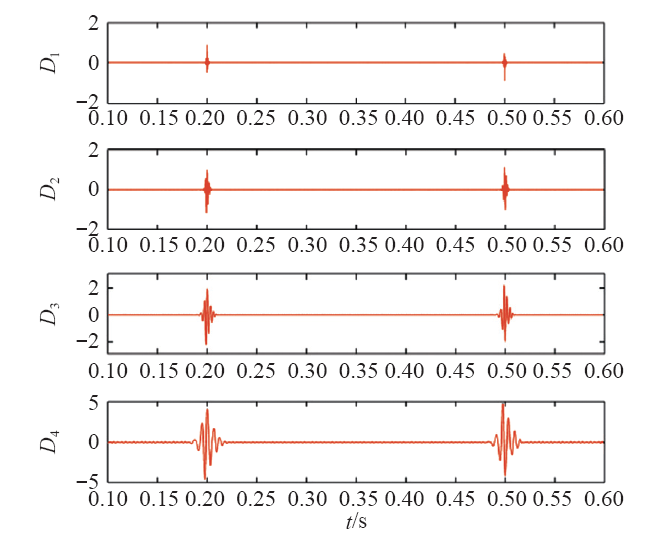
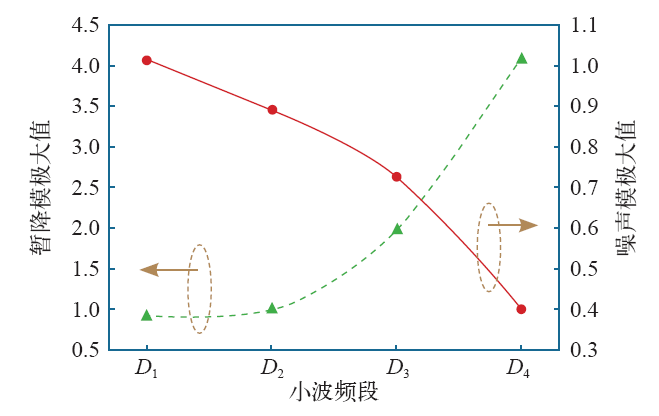
图3为暂降信号在小波变换各尺度的传播特性。可以看出,暂降为原始信号的一部分,分布在小波变换的各个高频尺度上,均呈现模极大值,随着分解尺度的增加,模极大值逐渐增大,在高频段D4呈现最大值。
图3
图3
暂降信号在小波各尺度的传播特性
Fig.3
Propagation characteristics of voltage sag at different wavelet scales
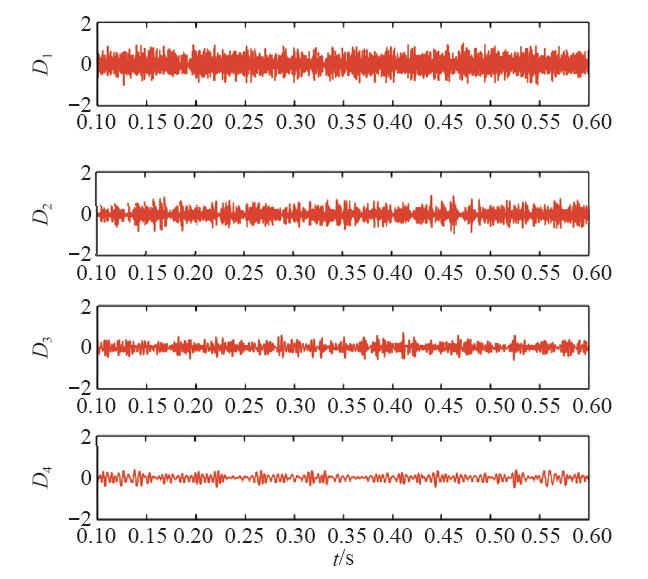
图4为噪声在小波各尺度的传播特性。可以看出,噪声作为干扰信号随机分布在小波变换的各个高频尺度上,噪声模值呈现负奇异特性,即在高频频段上较大,随尺度的增加逐渐减小,在低频频段上基本不存在。
图4
图4
噪声在小波各尺度的传播特性
Fig.4
Propagation characteristics of noise at different wavelet scales
图5为谐波在小波各尺度的传播特性。不同于噪声和暂降信号,各次谐波分布在指定高频频段中。3次谐波主要分布在D4频段中,13次谐波主要分布在D2频段中,基波信息分布在A4频段中。
图5
图5
谐波在小波各尺度的传播特性
Fig.5
Propagation characteristics of harmonic wave at different wavelet scales
综上所述,噪声、暂降和谐波在小波变换中具有以下传播特性:噪声和暂降分布于各个高频尺度上,而谐波存在于小波变换的特定高次频段中。如图6所示,噪声呈现与暂降相反的奇异性,对高频尺度特别是 D1、D2等高频频段具有较大影响,噪声和谐波(特别是高次谐波)的存在将导致模极大值变弱,影响电压暂降定位。
图6
图6
噪声与暂降在小波各尺度的模极大值
Fig.6
The modulus maximum of noise and sag at different wavelet scales
3.2 检测原理
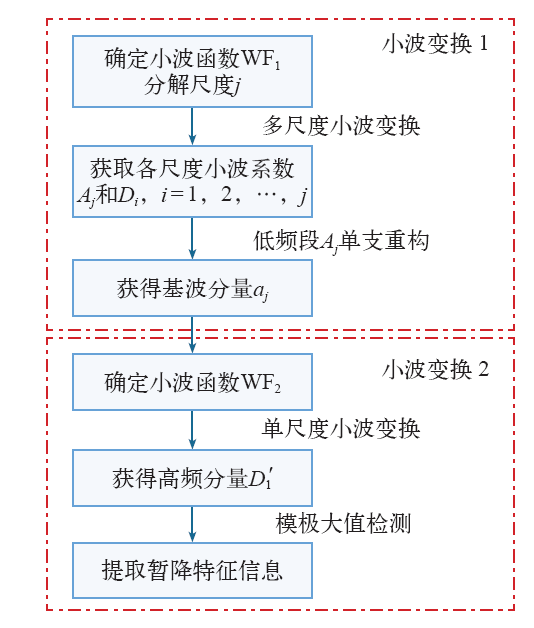
尽管噪声和谐波分布在小波变换高频频段并影响极大值的检测,但在最低频段噪声和谐波几乎没有影响。基于此,本文提出了一种利用双小波变换实现小波暂降的实时检测方法,在大尺度下提取分析电压基波成分,在小尺度下检测分析电压突变信息,从而准确定位电压暂降的起止时刻。如图7所示,双小波检测的具体步骤如下:
图7
(1)确定合适的尺度j,将原始信号进行多尺度小波分解,获得各尺度的小波系数。
(2)对最低频段Aj进行单支重构,得到含暂降信号的基波分量aj。
(3)对基波分量aj进行单尺度小波变换,获得高频分量D1′。
(4)通过检测高频分量D1′的模极大值,确定电压暂降的起止时刻。
3.3 消失矩阶数
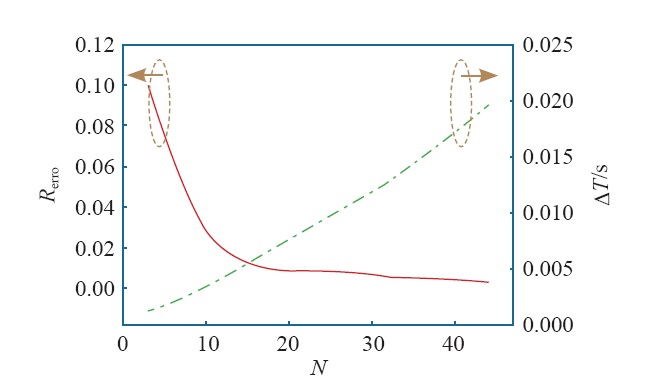
双小波检测中的关键是基波信息提取的精确性和暂降时刻检测的准确性,消失矩阶数表征小波函数逼近信号的收敛率,是小波分析的重要参数,本文选用db系小波函数作为研究对象,分别研究基波信息提取的精确度和暂降信息检测的准确度与消失矩阶数N的关系,为双小波检测中小波函数的选取提供支撑。以220V含30%电压暂降的工频信号为例,暂降检测的准确度和基波检测精度分别用偏离时间ΔT和误差率Rerro来表征,即
式中,t、A为检测的电压暂降时间和基波幅值;t0、A0为电压暂降发生的时间和基波实际幅值。分析结果如图8所示。
图8
图8
消失矩阶数对误差率及偏离时间的影响
Fig.8
The effect of vanishing moments on the error rate and time deviation
从图8可以看到,当消失矩阶数较小时,db小波对基波特征信息的提取误差较大;随着消失矩阶数的增加,db小波基波特征信息的提取精度越来越高,误差越来越小,在消失矩N = 10时具有明显的拐点;另一方面,当消失矩阶数较小时,暂降检测的时间误差较小,随着消失矩阶数的增加,暂降检测准确度逐渐降低,二者基本呈现线性关系。综合考虑时间延迟和提取精度影响,本文采用db20小波进行基波信息提取,db10小波进行暂降信息检测。
4 仿真分析
图9
图10
图11
图12
图12
双小波分析时延性分析结果
Fig.12
The time-delay analysis results of double wavelet analysis
5 结论
本文提出了一种双小波电压暂降检测方法,首先采用db20小波对电压暂降信号进行分解,在低频尺度进行单支重构获取含暂降的基波信号,再用db10小波对基波信号进行奇异性检测,精确确定暂降发生的起止时刻,并通过Matlab/Simulink进行仿真验证。仿真结果表明,双小波检测方法能够有效地抑制噪声和谐波干扰,具有较强的抗干扰能力,在同时含有噪声和谐波条件下也可实现电压暂降的准确定位,有效地提高了小波变换的检测性能。
参考文献
Wavelet based signal processing technique for classification of power quality disturbances
[C].
Applications of wavelets in electric power quality: voltage events
[J].
基于小波变换的自适应电网谐波检测方法研究
[J].
The study of self-adapt harmonic detection in power grid based on the wavelet transformation
[J].
A novel wavelet transform based voltage sag/swell detection algorithm
[J].
电压暂降检测方法分析
[J].
Analysis of detection methods of voltage sag
[J].
基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位
[J].<p>提出了用短时傅里叶变换作为时频信号分析工具研究电能质量扰动识别问题,同时提出了用奇异值分解技术研究扰动时间定位问题。从扰动电压信号短时傅里叶变换后得到的二维频谱幅值矩阵中提取出4个特征序列,生成频谱峰值曲线、基频幅值曲线、高频幅值曲线和幅值标准差曲线,这些曲线用6个特征量来表征。当6个特征量中的某几个满足一定的取值组合时能够唯一确定一种扰动,文中通过建立决策树,实现多种单一与复合扰动的识别。利用采样信号构造Hankel矩阵,对此矩阵进行奇异值分解,通过分量信号的构造并从中提取模极大值点,进行扰动时间定位。仿真结果表明,本文提出的方法能够实现8种单一与8种复合扰动的类型识别,准确检测出电压暂降、暂升、中断的幅值,并可对电压暂降、振荡、脉冲等扰动进行精确的扰动时间定位。</p>
Identification of power quality disturbance based on short-term Fourier transform and disturbance time orientation by singular value decomposition
[J].<p>提出了用短时傅里叶变换作为时频信号分析工具研究电能质量扰动识别问题,同时提出了用奇异值分解技术研究扰动时间定位问题。从扰动电压信号短时傅里叶变换后得到的二维频谱幅值矩阵中提取出4个特征序列,生成频谱峰值曲线、基频幅值曲线、高频幅值曲线和幅值标准差曲线,这些曲线用6个特征量来表征。当6个特征量中的某几个满足一定的取值组合时能够唯一确定一种扰动,文中通过建立决策树,实现多种单一与复合扰动的识别。利用采样信号构造Hankel矩阵,对此矩阵进行奇异值分解,通过分量信号的构造并从中提取模极大值点,进行扰动时间定位。仿真结果表明,本文提出的方法能够实现8种单一与8种复合扰动的类型识别,准确检测出电压暂降、暂升、中断的幅值,并可对电压暂降、振荡、脉冲等扰动进行精确的扰动时间定位。</p>
基于复小波变换和有效值算法的电压暂降检测方法
[J].
Voltage sag detection method based on complex wavelet transform and RMS algorithm
[J].
基于小波变换和改进Prony方法的电能质量扰动分析
[J].
Power quality disturbance analysis based on wavelet transform and improved Prony method
[J].
基于Hilbert -Huang变换和小波包能量谱的电压暂降源识别
[J].
Identification of voltage sags source based on Hilbert-Huang transform and wavelet packet wnergy spectrum
[J].
基于小波变换的暂态电能质量的检测与识别
[J].
The detection and identification of transient power quality based on wavelet transform
[J].
一种抗噪声的电压暂降时刻检测方法
[J].
A voltage sag time detection method with anti-noise feature
[J].
基于包含谐波模型的加权最小二乘估计算法的电压暂降检测方法
[J].
Voltage sag detection based on weighted least-squares estimation algorithm with harmonic models
[J].