1 引言
对于三电平PWM变换器,国内外学者提出了多种控制理论和方法。提出较早并广泛应用的是电网电压定向控制(Voltage Oriented Control,VOC)[5],它通过旋转变换将网侧三相电流解耦成有功电流和无功电流分量,从而分别构成有功电流和无功电流的闭环控制。VOC可以获得良好的动态性能以及稳态性能,但是它对电流内环比例积分调节器(Proportional Integral,PI)参数有较强的依赖性[6]。随着瞬时功率理论的发展,1998年Toshihiko Noguchi提出了直接功率控制(Direct Power Control,DPC)[7],引起了广泛关注。与VOC不同,DPC不需要电流的旋转变换,省去了内环PI调节器的设计,根据网侧电压的相位、有功及无功功率的误差信号,直接从离线的开关矢量表中选择一个合适的电压矢量对有功和无功进行直接控制,具有结构简单、动态响应速度快等优点[8]。但是,DPC有较高的功率脉动,谐波含量较大,开关频率并不固定。应用于三电平拓扑时由于中性点平衡及电压跳变等问题的限制,使得最优开关矢量表的设计比较困难[9]。
近年来,随着微处理器及数字信号处理技术的发展,模型预测控制理论(Model Predictive Control,MPC)逐渐在电力电子和电气传动领域得到越来越多的关注。MPC根据系统的历史信息和未来的输入去预测系统的未来输出,通过一个目标函数对不同的电压矢量进行枚举,选择使目标函数最小的电压矢量,并得到最优的开关序列[10]。相比DPC,模型预测控制不仅表现出类似的快速动态响应,而且在稳态性能上更加出色。
目前,国内外很多学者在离线参数辨识的基础上,结合现代控制理论以及系统辨识理论提出了各种在线参数辨识方法。通常可以采用递推最小二乘法、模型参考自适应法以及扩展卡尔曼滤波法等。最小二乘法最早是由Karl Gauss为预测行星轨道而提出的,如今已成为一种广泛的参数辨识方法[14,15]。最小二乘法理论因其概念简单,计算量较小,具有一致性、有效性和无偏性等统计特性,在实际工程中得到了广泛的使用,很适用于PWM变换器电感参数的在线辨识[16]。相比于最小二乘法,模型参考自适应参数辨识方法利用系统的数学模型对网侧电流进行预测[17],并根据采样到的实际电流值实时估算网侧电感值,具有动态响应快及鲁棒性强等特点,但是模型参数自适应方法的设计过程相对复杂[18]。扩展卡尔曼滤波法作为一种递推估算法[19],实际迭代过程中需要大量的矩阵运算,其计算较为繁琐,对于PWM变换器电感参数辨识并不实用。除了上述辨识算法外,还有人工智能法,如神经元网络、遗传控制及模糊控制等算法[20,21],但这类算法需要进行极为复杂的建模,不但会使控制系统变得复杂还会占用控制器大量的运算资源,在实际的电感参数辨识中并不适用,目前尚处于理论研究阶段。
传统的三电平PWM变换器模型预测控制算法需要27次功率预测,计算量较大。本文提出一种改进的模型预测控制方法,基于无差拍控制原理首先计算得到消除功率误差的参考电压矢量,然后再得到离参考电压最近的电压矢量,相比传统的基于27次功率预测的枚举计算,大大减少了计算量。最后,为了提高系统的鲁棒性,进一步引入了基于递推最小二乘法的电感参数在线辨识算法,使得PWM变换器在初始电感参数不准确的情况下仍能获得良好的控制精度和动态性能。仿真和实验结果验证了本文所提方法的有效性。
2 模型预测控制原理
2.1 传统模型预测控制
在各种模型预测控制方法中,有限控制集模型预测控制(Finite Control Set Model Predictive Control,FCS-MPC)凭借其无需调制策略、概念简单易于理解和可进行多目标协调控制等诸多优点得到了广泛的研究和应用。FCS-MPC用于三相PWM变换器时按照控制的变量可以分为模型预测功率控制(Finite Control Set Model Predictive Power Control,FCS-MPPC)和模型预测电流控制(Finite Control Set Model Predictive Current Control,FCS-MPCC)。FCS-MPPC的主要控制目标是使实际有功功率和无功功率能够准确跟踪参考值。
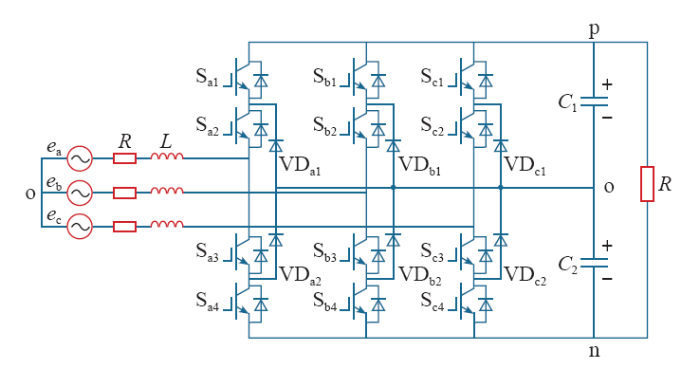
如图1所示,对于三电平拓扑来说,还需要控制中性点电位平衡,尽可能保证最小的直流母线电容压差。为了可以同时实现这几个目标,可以在目标函数中包含这几项控制目标,然后根据系统的预测模型,对所有候选电压矢量进行枚举,从中选择出可以使目标函数值最小的电压矢量作为输出。
图1
三电平PWM变换器采用FCS-MPPC时的目标函数定义为
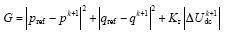
式中,前两项为有功功率和无功功率的跟踪误差;Kr为调节中性点电位平衡的权重系数;ΔUdck+1为直流侧上下两个母线电容的压差。中性点电位平衡控制的影响可通过权重系数Kr的大小进行增强或减弱。
在k + 1时刻,直流母线电容的压差ΔUdck+1可通过下式预测
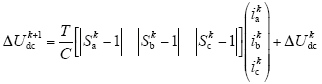
式中,Sak、Sbk和Sck为k时刻的开关状态函数;ΔUdck = ΔU kdc1 - ΔU kdc2为k时刻直流侧母线电容的压差;C = C1 = C2为直流母线电容。
k + 1时刻复功率S的预测值可以表示为
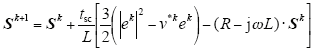
式中,tsc代表控制周期;上标“*”代表复矢量的共轭。为了实现单位功率因数,无功功率参考值qref设为零。因此,目标函数式(1)可简化为
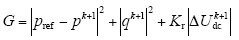
其中,pk+1 = Re(Sk+1);qk+1 = Im(Sk+1)。
由于数字系统存在控制延时,所以需要在k~ k + 1时刻对有功功率和无功功率进行一拍延时补偿,预测得到k + 1时刻的功率值。在k + 1~k + 2时刻,预测27个电压矢量对应的目标函数值,并选取出可以使目标函数达到最小值所对应的电压矢量,使得有功功率和无功功率都尽可能地接近给定参考值。
考虑一拍延时补偿的目标函数为
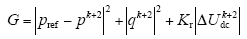
其中,pk+2、qk+2分别为复功率Sk+2的实部和虚部,且
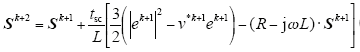
加入延迟补偿的传统FCS-MPPC的数学表达式为
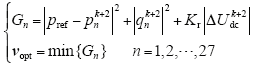
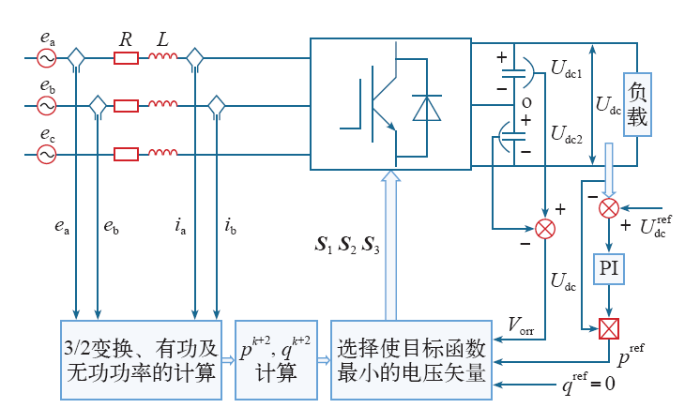
其中,vopt为最优的电压矢量。相应的整个系统的控制框图如图2所示。
图2
2.2 改进的模型预测控制
对于三电平PWM变换器而言,传统的FCS-MPPC需要27次功率预测计算,其概念简洁直观、易于理解。然而,由于选择最优电压矢量时需要多次功率预测,控制程序计算量较大,这种算法的弊端在更高电平的拓扑结构中会更加突出。为了降低计算量,本文提出一种高效模型预测控制(Efficient MPPC,E-MPPC),其特点是用参考电压矢量vref代替功率跟踪误差进行最优电压矢量选取,从而省去了27次功率预测计算,大大降低了程序计算量。
E-MPPC中参考电压矢量vref的计算根据功率无差拍控制的方法得到。将式(6)中的Sk+2用参考复功率Sref代替,重新整理式(6),可得参考电压矢量vref计算式为
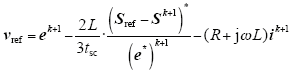
如果k + 2时刻变换器侧的输出电压矢量等于vref,那么复功率Sk+2将完全跟踪到参考值Sref,即实现精确的无差拍控制。然而这种传统的无差拍控制方式难以考虑系统约束,也不易于实现其他控制目标。因此本文在获取vref后仍采用基于最小化目标函数的方式确定最优电压矢量。
根据式(8),E-MPPC的目标函数可以定义为
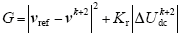
E-MPPC选择最优电压矢量的数学表达式为
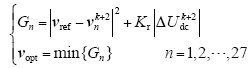
将式(6)代入式(10)并重新整理,得
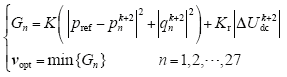
其中, 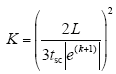
对比式(7)和式(11),可以发现改进的E-MPPC和传统的FCS-MPPC在形式上十分类似,二者区别在于改进方法多了一个正增益因子K。然而,如果式(9)右侧第一项除以一个增益因子K,即,如果Kr = Kr/K,那么最小化式(11)就等价于最小化式(7),也就是说两种方法最优电压矢量选择将完全一样,但是由式(7)可知改进方法省去了27次功率预测计算,具有较高的计算效率。此外,该方法可以进一步应用到两电平或更高电平拓扑结构中。
3 电感参数辨识原理
3.1 递推最小二乘法
最小二乘法是系统辨识中最基本的方法,它需要将测试的所有数据一次性计算,存储的数据较多,所占用内存较大,适用于离线参数辨识。对于在线参数辨识而言,该方法由于程序计算量较大,并没有得到广泛的使用。为了解决这个问题,降低数据的存储内存,提出了递推最小二乘法。该方法的系统存储内存较小,适用于在线参数辨识,其基本原理为:根据采样到的测量值和上一时刻的辨识参数值,通过迭代公式进行修正并得到当前时刻的辨识参数值,使其计算复杂度大大降低,并成为一种实用的在线参数辨识方法。
一个单变量线性时不变系统,对应n次输入变量和输出变量,其方程可表示为
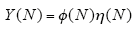
式中,Y(N)为系统输出序列;φ(N)为输入输出序列;η(N)为待辨识参数序列。
每采样一组新的数据,均对应一组新的输出数据,即
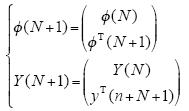
其中, 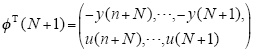
已知在基本最小二乘法中,待辨识的参数值为
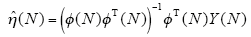
此时辨识的参数值$\hat{n}$可通过式(14)得到,即
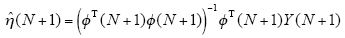
将式(13)代入式(15)中,可得
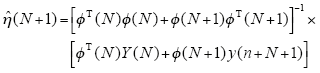
为了便于分析,令
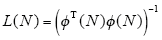
则
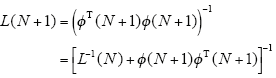
对上式进一步化简,得到
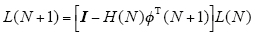
对式(16)进一步化简,可得
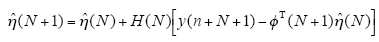
其中,I为n阶单位矩阵,H(N)表示为
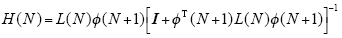
将采样得到的参数变量代入式(19)~式(21)进行迭代运算,即可得到系统的辨识参数值。需要指出的是,在利用上述公式进行迭代之前需要知道L(N)和$\hat{n}$(N)的初值,通常采取的方法是将二者的初值设为固定常数,即
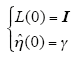
其中,I为单位矩阵;γ为极小的正实数常量。
利用式(22)所设定的初值及迭代公式式(19)~式(21)进行迭代运算,就可以得到系统参数的辨识值。
3.2 三电平PWM变换器辨识模型的建立
基于上述分析,为了辨识三电平PWM变换器的网侧电感值,则需要将系统数学模型转换成最小二乘法的标准定义形式,见式(12)。在两相dq坐标系下,三电平PWM变换器的数学模型表示为
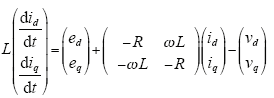
在稳态条件下,上式的电流微分项为零,式(23)进一步表示为
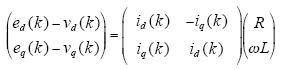
对比式(12),可知采样数据Ø(k)、输出数据 y(k)及辨识数据n(k)分别为
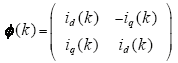
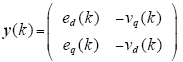
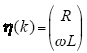
进一步整理式(19)~式(21),并结合式(25)~式(27),可得
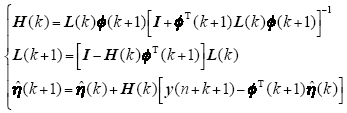
式中, 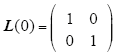
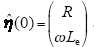
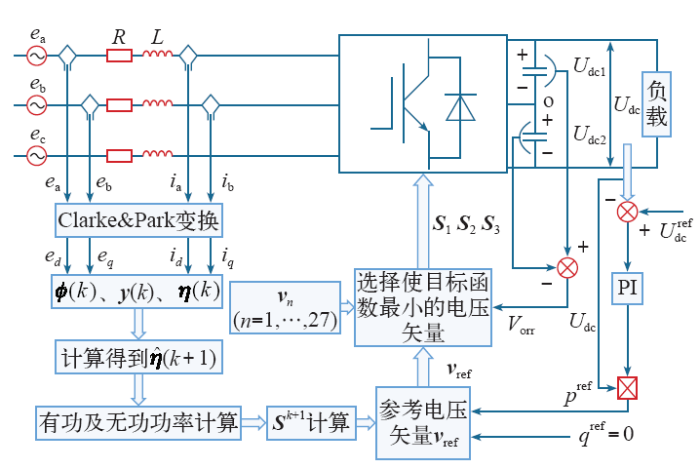
加入电感参数辨识的改进的E-MPPC的系统控制原理如图3所示。
图3
图3
带参数辨识功能的E-MPPC原理图
Fig.3
Control diagram of the proposed E-MPPC with parameter identification
4 仿真结果
本文将基于递推最小二乘法的电感参数辨识加入到改进的模型预测控制中进行了仿真验证,仿真参数见下表。
表 系统控制参数
Tab
| 参 数 | 数 值 |
|---|---|
| 电感电阻R/Ω | 0.3 |
| 电感L/mH | 10 |
| 直流母线电容C/μF | 470 |
| 负载RL/Ω | 97 |
| 线电压UN /V | 150 |
| 电网频率f /Hz | 50 |
| 采样频率fs /kHz | 20 |
| 直流母线电压Udc /V | 300 |
| 权重系数Kr | 100 |
| 增益常数K | 0.395 2 |
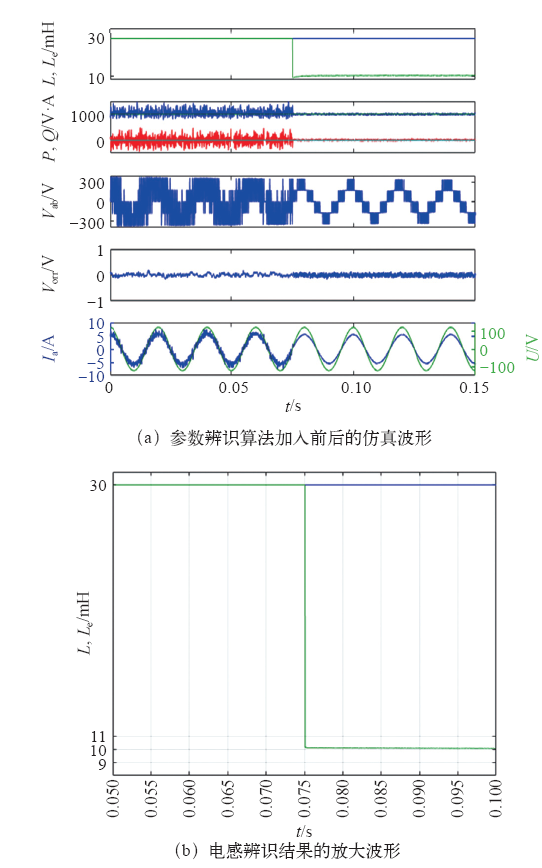
图4
图4
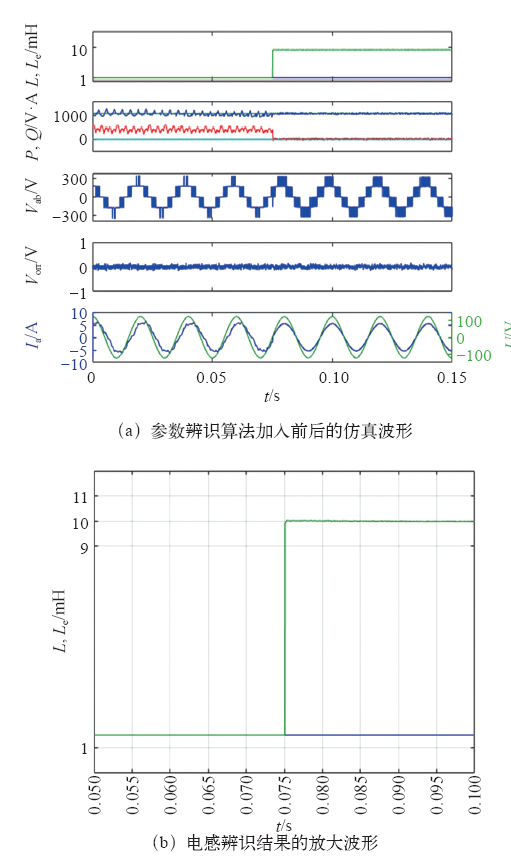
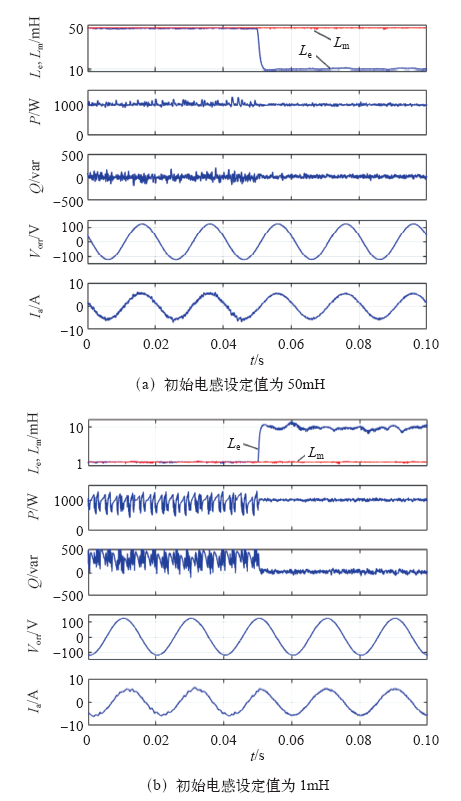
电感初始设定值为30mH的辨识仿真结果
Fig.4
Simulated result with initial inductance value of 30 mH
图5
图5
电感初始设定值为1mH的辨识仿真结果
Fig.5
Simulated result with initial inductance value of 1 mH
5 实验结果
为了验证改进E-MPPC的有效性,通过实验对传统FCS-MPC和改进E-MPPC二者的运行效果进行对比,实验参数见表1。实验波形中除电压和电流波形有探头可以直接测量外,其他内部变量均通过控制板上的DA得到,采用录波仪DL850记录数据,然后导出到Matlab进行画图和分析。
图6
图6
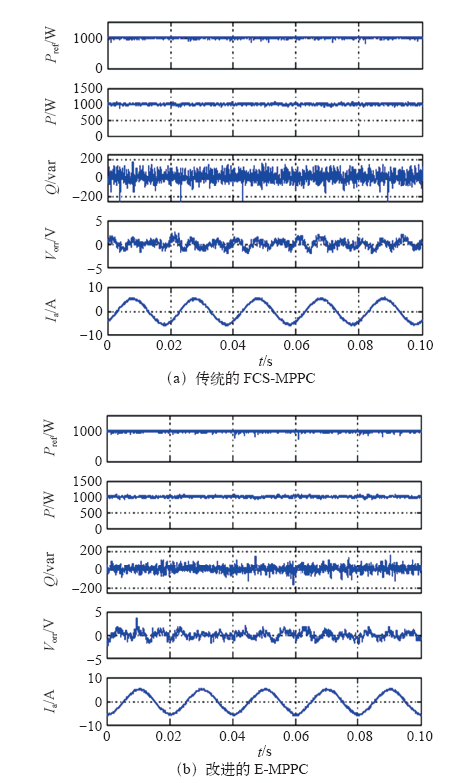
稳态实验波形(P = 1 000W,Q = 0var)
Fig.6
Steady state response (P = 1 000W, Q = 0var)
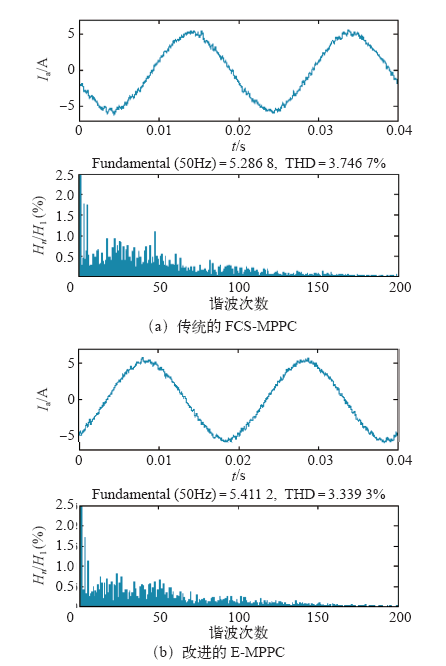
网侧THD和频谱分析如图7所示,可以看出,改进的E-MPPC的电流THD要略低于传统的FCS-MPPC。
图7
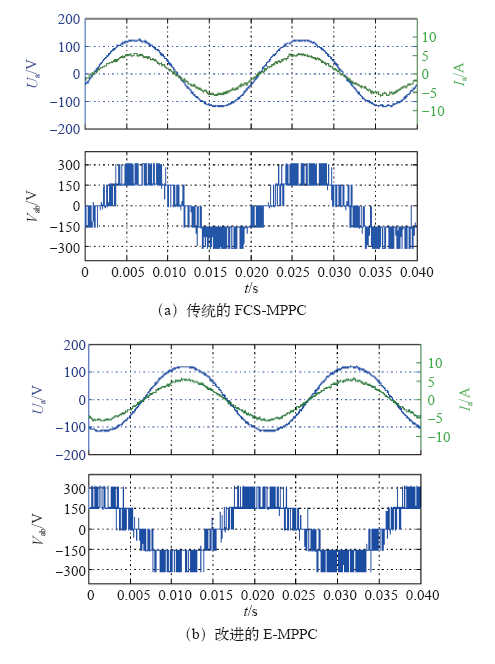
图8是网侧相电压Ua、网侧相电流Ia和网侧线电压Vab的实验波形。可以看出,两种方法均没有产生电压幅值过高跳变的问题,网侧电压和电流同相位,实现了网侧单位功率因数控制。
图8
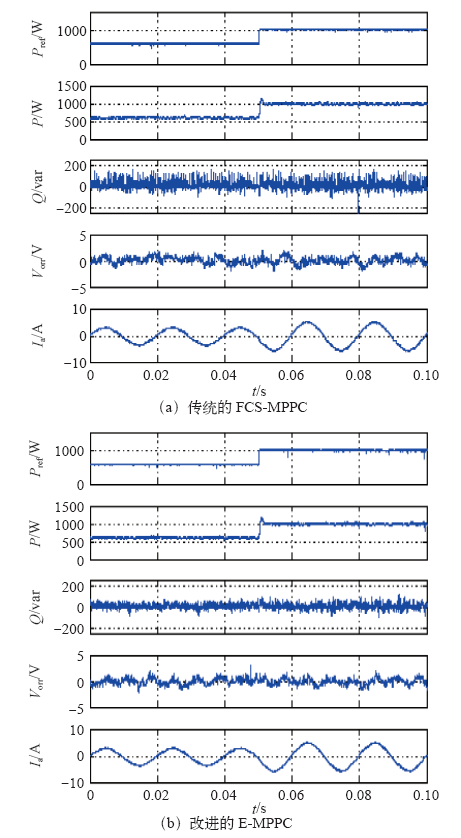
图9是由600W功率阶跃到1 000W的动态实验波形,可以看出两种方法表现出了极为相似的动态特性,有功功率均准确地跟踪了参考值。此外,改进的方法表现出了较低的功率脉动和较小的电流THD。
图9
图9
动态实验波形(P = 1 000W,Q = 0var)
Fig.9
Response to power increase (P = 1 000W, Q = 0var)
需要指出的是,由于改进的E-MPPC用参考电压矢量vref代替功率跟踪误差进行最优电压矢量选取,省去了传统FCS-MPPC中繁复的多次功率预测计算,因此显著减小了系统的复杂度和计算量。实验中对两种方法的程序执行时间进行了测量,改进的E-MPPC程序运行时间为29.67 μs,而传统的FCS-MPPC的程序运行时间为42.56 μs。由此可见改进的E-MPPC在程序执行效率上更加高效。
图10
图10
电感辨识算法加入前后的实验结果
Fig.10
Experimental result when enabling inductance identification
6 结论
本文在分析三电平PWM变换器改进的模型预测控制和最小二乘法参数辨识原理的基础上,将递推最小二乘法应用于三电平PWM变换器的电感参数辨识上,并与以参考电压矢量进行最优电压矢量选择的改进的模型预测算法相结合,提高了控制方法的控制性能。实验结果表明,所辨识的电感参数值接近于实际电感值但是不完全相等,而且利用加入递推最小二乘法电感参数辨识之后的电感值进行系统控制,系统的功率脉动和电流THD均有明显降低。由此可见,加入了递推最小二乘法电感参数辨识的模型预测控制的可行性和有效性。
参考文献
Back-to-back双三电平励磁同步电机矢量控制系统
[J].以基于Back-to-Back双三电平功率变换器电励磁同步电机矢量控制为研究对象, 提出了适用于全速范围的全阶闭环气隙磁链观测器, 阐明了其内部基于滤波器特性的电流-电压模型之间的平滑切换机理。三电平有源前端实现网侧的单位功率因数运行, 减少对电网污染的同时实现能量的双向流动。同时引入具有自适应调节中点电位的简化三电平电压空间矢量脉宽调制(SVPWM)策略, 并在此基础上提出新颖的三电平功率变换器相电压重构算法。现场运行结果表明基于Back-to-Back双三电平功率变换器电励磁同步电机矢量控制解决方案具有优良的控制性能, 真正实现了节能调速和绿色环保的高度结合。
Vector control system of electrically excited synchronous motor fed by back-to-back dual three-level converte
[J].以基于Back-to-Back双三电平功率变换器电励磁同步电机矢量控制为研究对象, 提出了适用于全速范围的全阶闭环气隙磁链观测器, 阐明了其内部基于滤波器特性的电流-电压模型之间的平滑切换机理。三电平有源前端实现网侧的单位功率因数运行, 减少对电网污染的同时实现能量的双向流动。同时引入具有自适应调节中点电位的简化三电平电压空间矢量脉宽调制(SVPWM)策略, 并在此基础上提出新颖的三电平功率变换器相电压重构算法。现场运行结果表明基于Back-to-Back双三电平功率变换器电励磁同步电机矢量控制解决方案具有优良的控制性能, 真正实现了节能调速和绿色环保的高度结合。
基于模块化多电平变流器的柔性直流输电技术
[J].
The introduction of technology of HVDC based on modular multi-level converter
[J].
高性能大容量交流电机调速技术的现状及展望
[J].
High performance and high power AC motor variable speed drives-status and trends
[J].
A new mathematical model and control of a three-phase AC-DC voltage source converter
[J].
An improved deadbeat scheme with fuzzy controller for the grid-side three-phase PWM Boost rectifier
[J].
Directi power control of PWM converter without power-source voltage sensors
[J].
Performance improvement of direct power control of PWM rectifier with simple calculation
[J].
Table-based direct power control for three-level neutral point-clamped pulse-width modulated rectifier
[J].
A brief overview of model predictive control
[J].
Efficient model predictive power control for three-level AC/DC converters
[C].
Low-complexity model predictive power control: double-vector-based approach
[J].
Model predictive direct power control of a PWM rectifier with duty cycle optimization
[J].
A nonlinear least-squares approach for identification of the induction motor parameters
[J].
基于递推最小二乘算法的感应电动机参数离线辨识
[J].<p>感应电动机参数离辨识是实现高性能变频调速的前提。对基于递推最小二乘(recursive least-squares,RLS)算法的电机参数离线辨识的具体实现进行了详细阐述;基于离线辨识时电机的静止特性,简化了电机数学模型,减少了计算量;采用改进欧拉数值解法,求解巴特沃思数字滤波状态方程,既可获得信号的滤波值,同时又直接解得了信号的1阶和2阶导数值,避免了导数离散化的误差影响,提高了运算精度;运用线性反馈移位寄存器产生伪随机白噪声序列(M序列),作为辨识的激励信号;针对不同功率的电机进行了大量的仿真和实验研究,实验结果表明所提方法稳定性良好,辨识结果的一致性和准确性较高。</p>
Off-line parameter identification of induction motor based on recursive least-squares algorithm
[J].<p>感应电动机参数离辨识是实现高性能变频调速的前提。对基于递推最小二乘(recursive least-squares,RLS)算法的电机参数离线辨识的具体实现进行了详细阐述;基于离线辨识时电机的静止特性,简化了电机数学模型,减少了计算量;采用改进欧拉数值解法,求解巴特沃思数字滤波状态方程,既可获得信号的滤波值,同时又直接解得了信号的1阶和2阶导数值,避免了导数离散化的误差影响,提高了运算精度;运用线性反馈移位寄存器产生伪随机白噪声序列(M序列),作为辨识的激励信号;针对不同功率的电机进行了大量的仿真和实验研究,实验结果表明所提方法稳定性良好,辨识结果的一致性和准确性较高。</p>
Predictive-control-based direct power control with an adaptive parameter identification technique for improved AFE performance
[J].
三相电压型PWM整流器模型自校正预测控制
[J].<p>针对传统模型预测控制(MPC)对模型依赖性强,鲁棒性能较差的问题,提出了一种模型自校正预测控制。根据三相电压型PWM整流器的模型计算预测电流值和实际电流值估算实际模型参数值。算法可实时对模型参数进行修正,消除模型参数不匹配对系统的影响,增强控制系统鲁棒性。仿真与实验结果表明,所提模型自校正预测控制算法在模型参数变化时具有较强的鲁棒性,可显著提高MPC的控制品质。</p>
Predictive control of three-phase voltage source PWM rectifiers based on model self-correction
[J].<p>针对传统模型预测控制(MPC)对模型依赖性强,鲁棒性能较差的问题,提出了一种模型自校正预测控制。根据三相电压型PWM整流器的模型计算预测电流值和实际电流值估算实际模型参数值。算法可实时对模型参数进行修正,消除模型参数不匹配对系统的影响,增强控制系统鲁棒性。仿真与实验结果表明,所提模型自校正预测控制算法在模型参数变化时具有较强的鲁棒性,可显著提高MPC的控制品质。</p>
矢量控制中感应电动机转子电阻的自适应辨识
[J].
Rotor resistent adaptive identification for vector control of induction motors
[J].
Application of genetic algorithm with a novel adaptive scheme for the identification of induction machine parameters
[J].
基于Hopfield神经网络的线性系统参数辨识方案及在鼠笼式电机传动系统参数辨识中的应用研究
[J].
Hopfield neural network based linear system parameters’ identification scheme and its application in asynchronous motor drive system identification
[J].
三电平变换器模型预测控制研究
[D].
Parameter identification of induction motors using differential evolution
[J].
Identification of wiener systems with clipped observations
[J].
Parameter identification of induction motors using differential evolution
[C].
Low-complexity model predictive power control-single vector-based approach
[J].