电气工程学报, 2018, 13(11): 30-36 doi: 10.11985/2018.11.004

直流电缆主绝缘与屏蔽层界面形貌对电场畸变的仿真研究

尹毅1, 吴建东1, 胡嘉磊1, 张磊2,3, 孙璐2,3, 沈耀军2,3

1. 上海交通大学电子信息与电气工程学院电气工程系 上海 200240

2. 国网浙江省电力有限公司舟山供电公司 舟山 316021

3. 浙江舟山海洋输电研究院 舟山 316021

Simulation of Electric Field Distortion Caused by Interface Morphology Between Insulation and Shielding in HVDC Cables

Yin Yi1, Wu Jiandong1, Hu Jialei1, Zhang Lei2,3, Sun Lu2,3, Shen Yaojun2,3

1. Shanghai Jiao Tong University Shanghai 200240 China

2. Zhoushan Power Supply Company of State Grid Zhejiang Electric Power Co., Ltd. Zhoushan 316021 China

3. Zhejiang Zhoushan Marine Power Research Institute Zhoushan 316021 China

收稿日期: 2018-08-3   网络出版日期: 2018-11-30

基金资助: 国网科技项目《±320kV及以下柔性直流电缆性能评价体系研究》.  52110116004Z

Received: 2018-08-3   Online: 2018-11-30

作者简介 About authors

尹 毅 男 1972年生,博士,教授,博士生导师,主要从事电介质物理理论与相关测试技术等方面的研究工作。

吴建东 男 1982年生,博士,副研究员,主要从事电介质物理理论与相关测试技术等方面的研究工作。

摘要

高压直流电缆中,主绝缘与屏蔽层的界面形貌,引起界面附近主绝缘内电场的畸变,是造成电缆绝缘故障的原因之一。这种界面形貌形成的机理与屏蔽层中掺杂的炭黑颗粒有关,在生产过程中,这些颗粒进入主绝缘内,形成局部凸起,引发电场集中。本文从该机理出发,基于随机过程建立界面形貌的几何模型,有限元仿真计算界面附近的电场分布,从统计的意义上,研究该界面形貌对电场畸变的影响。结果表明,为降低界面形貌引起的电场畸变,最有效的方法之一是增大屏蔽层中掺杂炭黑颗粒的粒径和减小这些颗粒进入主绝缘的深度。若屏蔽层中有不可去除的小粒径颗粒,则可以掺杂大颗粒炭黑从概率上减小电场畸变。

关键词： 界面形貌 ; 直流电缆 ; 随机过程 ; 有限元 ; 仿真

Abstract

In HVDC cables, the interface morphology between insulation and shielding will cause electric field distortion. This is one of the reasons of cable insulation faults. Such morphology is related to the carbon black particles added in the shielding. In the process of cable production, these carbon black particles may enter insulation, form bulges on the interface, and thus cause electric field concentration. In this paper, the above mechanism is considered. Geometric model of such morphology is established based on stochastic process. Finite element method is used to solve electric field distribution near the interface. Electric field distortion caused by interface morphology is studied from the aspect of statistics. As results show, to reduces such distortion, one of the most effective methods is increase carbon black particle diameter or reduce the depth of particle entry. If there are small and unremovable particles in the shielding, it is recommended that big carbon black particles should be added.

Keywords： Interface morphology ; HVDC cable ; stochastic process ; finite element method ; simulation

PDF (2861KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

尹毅, 吴建东, 胡嘉磊, 张磊, 孙璐, 沈耀军. 直流电缆主绝缘与屏蔽层界面形貌对电场畸变的仿真研究. 电气工程学报[J], 2018, 13(11): 30-36 doi:10.11985/2018.11.004

Yin Yi. Simulation of Electric Field Distortion Caused by Interface Morphology Between Insulation and Shielding in HVDC Cables. Journal of Electrical Engineering[J], 2018, 13(11): 30-36 doi:10.11985/2018.11.004

1 引言

相较传统的交流输电,高压直流（HVDC）输电具有经济优势,随着技术的不断进步,其应用也将日趋广泛[1]。其中,电缆绝缘是十分重要的一环,不恰当的电缆绝缘可能造成弱点击穿,导致整个输电系统故障[2,3]。

仿真是研究高压直流电缆内电场分布的方法之一。近年来,得益于对电缆绝缘内电场分布机理的了解和计算机速度的提升,研究者可以通过仿真计算电缆绝缘内的电场分布,分析影响电场分布的因素,并通过控制这些因素提高电缆运行的安全性。这些因素包括：非稳态电场[4]、非线性电导[5]、空间电荷[6,7]、接头结构[8]、温度梯度[9]和热瞬态[10,11]等。

主绝缘与屏蔽层的界面形貌也对电缆电场分布有很大影响。很多企业在电缆制造中强调该界面的光滑程度[12,13,14],研究者也有初步的仿真研究[15]。但这些研究都没有涉及界面形貌的产生机理,对形貌的描述也较为粗糙。

本文从高压直流电缆主绝缘与屏蔽层界面形貌产生的机理出发,基于随机过程建立界面形貌的几何模型,基于有限元仿真计算界面附近的电场分布,从统计的意义上,研究该界面形貌对电场畸变的影响。

2 模型的建立

2.1 几何模型

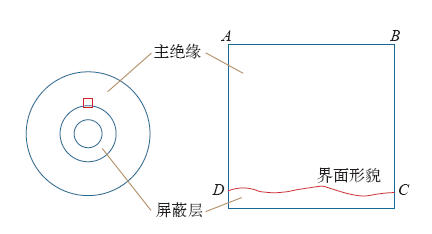
相较于电缆绝缘,高压直流电缆主绝缘与屏蔽层的界面形貌在几何尺寸上非常小,界面形貌也仅能影响界面附近的电场分布,因此几何建模中无需建立整个电缆绝缘与屏蔽层,仅需建立局部界面附近的模型。如图1所示,以内屏蔽层为例,左侧为电缆横截面,主绝缘和屏蔽层的界面是圆形,选取圆上的一段弧长为例,形成右侧的局部界面模型。其中,曲边矩形ABCD为主绝缘,其内部电场存在畸变,曲边CD为界面形貌,是引起电场畸变的原因。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   局部界面形貌的模型

Fig.1   Model of local interface morphology


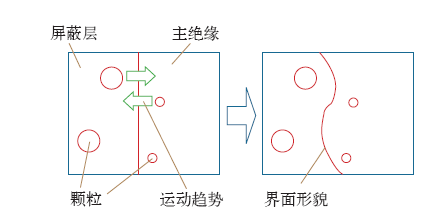
当前,高压直流电缆主绝缘和屏蔽层材料的基料主要是聚乙烯等高分子聚合物,主绝缘中一般添加少量纳米颗粒,屏蔽层中一般添加炭黑微米颗粒。三层共挤时,由于温度差、压强差和浓度差等原因,这些颗粒有进入对方材料的趋势,造成微观界面上的凹凸,形成不规则的界面形貌,如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   主绝缘与屏蔽层界面形貌形成的机理

Fig.2   Mechanism of interface morphology between shielding and insulation


由于主绝缘添加颗粒的粒径通常较小,含量也较少,因此几何建模中仅考虑屏蔽层材料中的炭黑颗粒。首先考虑只有一个炭黑颗粒的情况,假定炭黑颗粒的粒径为2R,进入主绝缘中的距离为h,则几何模型如图3所示。假定炭黑颗粒进入前,主绝缘是100μm见方的区域,炭黑颗粒从下方正中进入,此时界面的表面形貌中有一个凸起。其次考虑两个距离较近的炭黑颗粒同时进入的情况,此时两个炭黑颗粒对电场的畸变可能为非线性叠加。假定这两个炭黑颗粒的粒径分别为2R1和2R2,进入主绝缘中的距离分别为h1和h2,进入的位置距y轴的水平距离分别为w1和w2,则几何建模如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   单个炭黑颗粒的几何建模

Fig.3   Geometric modeling of single carbon black particle case


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   两个炭黑颗粒的几何建模

Fig.4   Geometric modeling of double carbon black particles case


考虑到炭黑颗粒的粒径、进入距离和颗粒间距离都是随机过程,因此几何建模中各参数均为概率分布。假定这些分布都满足正态分布,如式（1）~ 式（5）所示。

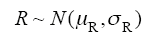
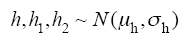
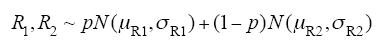
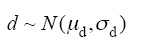
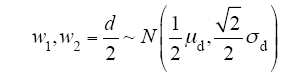
式中,N表示正态分布,其余均为常数。式（1）假定炭黑颗粒的粒径分布为正态分布。式（2）假定炭黑进入主绝缘的距离分布为正态分布。式（3）中,R1和R2的分布为两个正态分布的叠加,用于仿真屏蔽层中有粒径相差较大的两种颗粒的情况,两种颗粒可能是两种粒径级别的炭黑颗粒,也可能是炭黑颗粒与其他杂质,系数p用来控制两种颗粒的数量。式（4）假定两个炭黑情况下,炭黑之间的水平距离分布为正态分布。式（5）假定几何建模左右对称情况下,按式（4）求得的水平坐标分布。

2.2 方程与材料

直流电缆中,在不考虑老化等材料变性和操作雷电等过电压情况下,电场为稳态分布。若忽略空间电荷,则此时的电场由式（6）和式（7）描述。

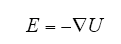
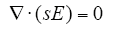
式中,E为电场;U为电压;s为电导率。式（6）说明电场是无旋场,式（7）说明电流是无源场。

几何建模中,计算区域仅有主绝缘和屏蔽层两种材料,而屏蔽层的电导率远大于主绝缘,因此可忽略屏蔽层中的电场。此时计算区域仅有主绝缘,若再忽略绝缘电导率的非线性,则电导率在全计算区域内为常数。此时可消去电导率,得式（8）,待求变量电压是标量场。

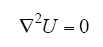
2.3 边界条件

偏微分方程的定解需要边界条件,即知道计算区域边界上,待求函数的函数值或其法向梯度值。如图1所示,计算区域为电缆的一部分,曲边CD通过屏蔽层与电缆导体接触,而屏蔽层的电导很大,因此该处边界条件如式（9）所示,即边界电压为电缆导体电压。

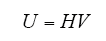
电缆具有对称性,横截面上电场沿径向分布。在计算区域较小时,直边BC和DA的延长线近似通过电缆横截面的圆心,因此该处边界条件近似为零法向梯度,如式（10）所示,其中,n表示边界法向量。

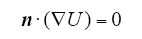
在不考虑电导非线性时,电缆主绝缘中的电场自内向外逐渐减小,当计算区域足够小时,直边AB与曲边CD足够接近,可认为AB上的电场接近主绝缘内径的平均场强,此时边界条件如式（11）所示,其中Eav表示主绝缘内径的平均场强,也是计算区域内的电场平均值。

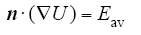
3 模型的求解

有限元是求解偏微分方程的有效方法之一,通过计算区域的离散化,求解待求函数在若干位置处的近似值。离散化过程越精细,则结果越接近真实值,花费的计算时间也越多,因此有限元求解时需要权衡精度和时间。

对于求解得到的电压,经过离散求导可以得到梯度,即电场。电场畸变率定义为电场与平均电场的比值,如式（12）所示。

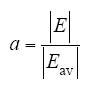
而绝缘故障通常从电场畸变最大的地方开始,因此需要关注最大的电场畸变率,如式（13）所示。

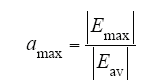
此外,由方程和边界条件的特性可知,式（9）中HV的取值对电压的影响是一个常数,求导后并不影响电场。Eav的作用类似,对电场仅仅是一个比例系数的作用,在式（12）和式（13）的计算过程中被消去,因此电场畸变率与HV和Eav的取值无关,而仅由式（1）~式（5）中的界面形貌特性决定。

4 模型的典型计算结果

对式（1）~式（5）进行一次随机过程,获得一组形貌参数,可用于几何建模。进而根据方程和边界条件,用有限元方法计算电缆主绝缘内靠近屏蔽层的电场分布。

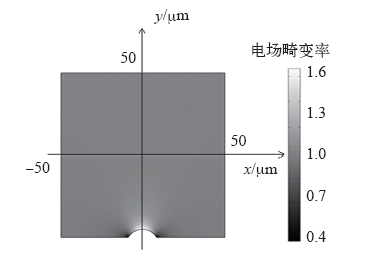
典型的单个炭黑颗粒情况下的计算结果如图5所示。电场畸变率最大出现在炭黑颗粒上方,类似尖端效应。炭黑颗粒上方电场左右分布对称,炭黑颗粒左右两侧电场较小。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   单个炭黑颗粒情况下的典型结果

Fig.5   Typical results in single carbon black particle case


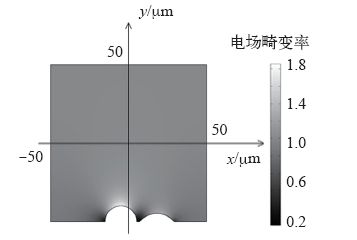
典型的两个炭黑颗粒情况下的计算结果如图6所示。电场畸变率最大出现在左侧炭黑颗粒的上方,右侧炭黑颗粒的顶端也有电场集中现象。两个炭黑颗粒上方电场左右分布不对称,说明两个炭黑周围的电场互相影响,即对电场的畸变为非线性叠加。炭黑颗粒左右两侧电场较小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   两个炭黑颗粒情况下的典型结果

Fig.6   Typical results in double carbon black particles case


5 模型的统计结果

5.1 单个炭黑颗粒的情况

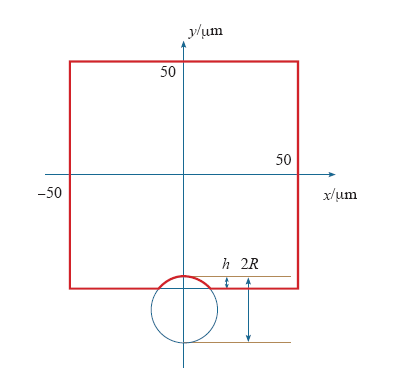
对式（1）和式（2）中的正态分布参数取值,并多次进行随机过程,生成多个和图3类似的单个炭黑颗粒进入主绝缘的几何模型。每个几何模型都按照式（8）和边界条件式（9）~式（11）计算式（13）中的最大电场畸变,最终获得随机过程下最大电场畸变率的分布。

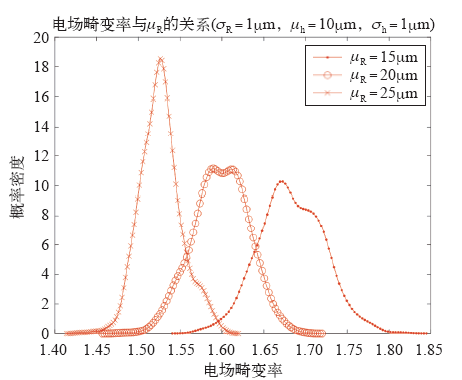
固定式（1）中炭黑颗粒半径分布的标准差为1μm,式（2）中进入深度分布的均值和标准差分别为10μm和1μm,改变式（1）中炭黑颗粒半径分布的均值分别为15μm、20μm、25μm,分别进行1 000次,总共3 000次随机过程。最终求得最大的电场畸变率分布如图7所示。从分布的范围看,粒径均值越小,电场畸变率越大,这与电场在尖端集中,尖端曲率半径越小,电场越集中的情况一致。从分布的形状看,粒径均值越小,电场畸变率的分布越分散,即小颗粒掺杂会对电场分布带来更大的不确定性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   单个炭黑颗粒情况下粒径均值的影响

Fig.7   Influence of μR in single carbon black particle case


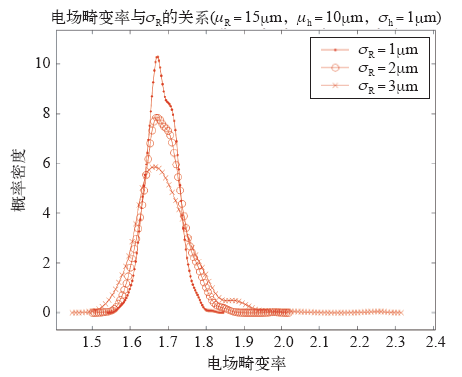
固定式（1）中颗粒半径分布的均值、式（2）中进入深度分布的均值和标准差,改变式（1）中颗粒半径分布的标准差,每个标准差进行1 000次随机过程,结果如图8所示。从分布范围看,粒径标准差的影响有限,3条曲线都集中在畸变率1.6~1.8范围内,当粒径标准差增大时,电场畸变率有增大的趋势,这说明在屏蔽层材料配方过程中掺杂颗粒粒径的统一有助于减小电场畸变,但改善作用有限。从分布的形状看,不同粒径标准差情况下的分散性类似。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   单个炭黑颗粒情况下粒径标准差的影响

Fig.8   Influence of σR in single carbon black particle case


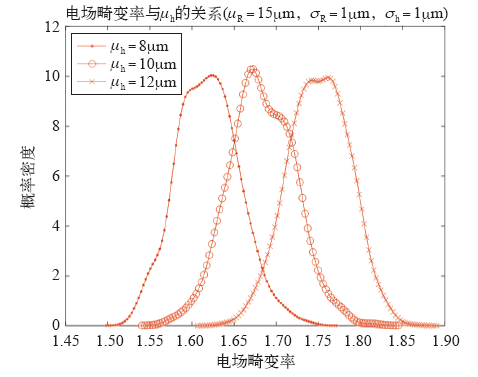
改变式（2）中炭黑颗粒进入深度分布的均值,固定式（1）和式（2）其余参数时,仿真结果如图9所示。从分布的范围看,进入深度均值越小,电场畸变率分布整体越小,这与工业生产中追求主绝缘和屏蔽层界面的光滑程度一致。从分布的形状看,不同进入深度均值情况下的分散性类似。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   单个炭黑颗粒情况下进入深度均值的影响

Fig.9   Influence of μh in single carbon black particle case


最后改变式（2）中炭黑颗粒进入深度分布的标准差,计算结果如图10所示。分布的范围和形状都与图8类似,说明改变炭黑颗粒进入深度分布的标准差对电场畸变有一定影响,但影响有限。

图10

新窗口打开| 下载原图ZIP| 生成PPT

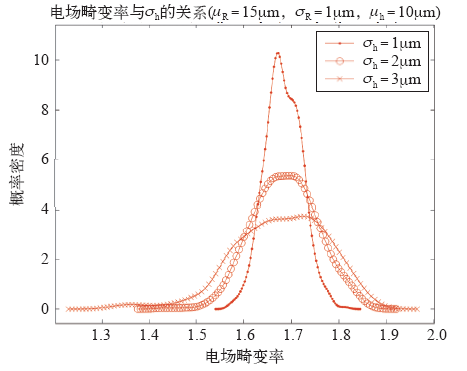
图10   单个炭黑颗粒情况下进入深度标准差的影响

Fig.10   Influence of σh in single carbon black particle case


5.2 两个炭黑颗粒的情况

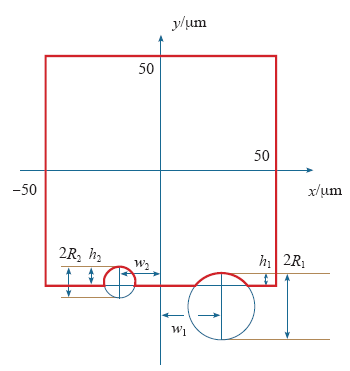
与单个炭黑颗粒的情况类似,对式（2）~ 式（4）中的参数取值,按式（2）~式（5）进行随机过程,最终按式（13）计算电场畸变率的最大值。由于两个炭黑情况下,主要关注炭黑之间的关系,因此将一些参数始终视为常数：μh = 10μm,σh = 1μm,μR1 = 15μm,σR1 = 1μm,μR2 = 20μm,σR2 = 1μm。

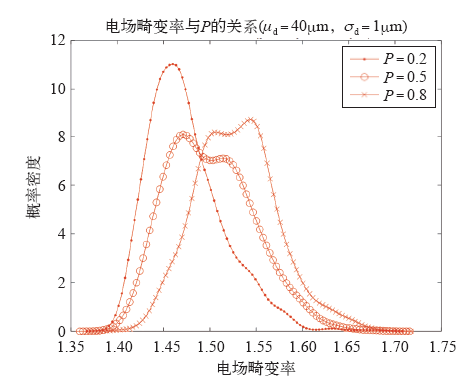
固定式（4）中炭黑颗粒间水平距离分布的均值和标准差分别为40μm和1μm,改变式（3）中的概率系数,仿真结果如图11所示。从分布范围上看,3条曲线能达到的最大最小值类似,这是因为不同的粒径组合出现概率虽然不同,但在不同概率系数的情况下都可以取到。从分布的形状看,当以大粒径颗粒为主时,电场畸变率偏小,且分布较为集中,这说明,若小颗粒杂质不可避免,则掺杂较多的大颗粒炭黑,相当于提高概率系数p,有助减小电场畸变率,虽然这种减小是概率性的。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   两个炭黑颗粒情况下概率系数的影响

Fig.11   Influence of p in double carbon black particles case


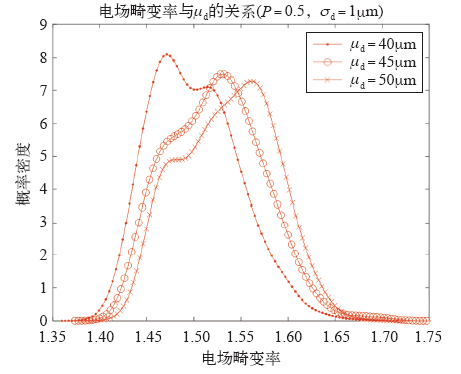
改变式（4）中炭黑水平距离分布的均值,结果如图12所示。从分布的范围看,水平距离均值越小,电场畸变率越小,但影响有限。从分布的形状看,水平距离均值越小,电场畸变率分布向减小的方向集中。而颗粒水平距离与掺杂的总量有关,因此掺杂越多,颗粒水平距离均值越小,电场畸变率有概率地下降。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   两个炭黑颗粒情况下水平距离均值的影响

Fig.12   Influence of μd in double carbon black particles case


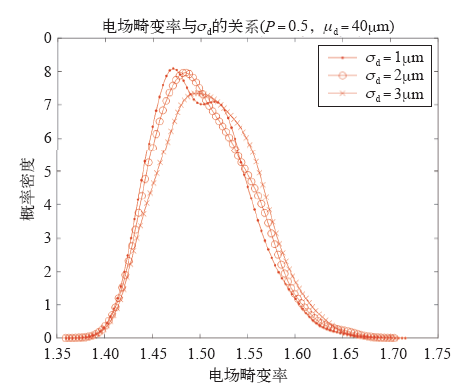
最后改变式（4）中炭黑水平距离分布的标准差,结果如图13所示。整体上,3条曲线形状和趋势一致,标准差越小,电场畸变率向着减小的方向集中。而炭黑水平距离与掺杂的均匀程度有关,说明掺杂越均匀,电场畸变率越有概率减小。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   两个炭黑颗粒情况下水平距离标准差的影响

Fig.13   Influence of σd in double carbon black particles case


6 结论

本文从高压直流电缆主绝缘与屏蔽层界面形貌产生的机理出发,基于随机过程建立界面形貌的几何模型,基于有限元仿真计算界面附近的电场分布,从统计的意义上,研究该界面形貌对电场畸变的影响。

根据单个炭黑颗粒情况的统计结果,为降低界面形貌引起的电场畸变,最有效的方法是增大屏蔽层中掺杂炭黑颗粒的粒径和减小这些颗粒进入主绝缘的深度。在此基础上提高炭黑颗粒粒径和进入深度的均一性有助降低电场畸变,但作用有限。

根据两个炭黑颗粒情况的统计结果,若屏蔽层中存在不可去除的小颗粒杂质,则可以通过掺杂大颗粒炭黑、掺杂更多炭黑和保持掺杂均匀等手段,在概率上降低电场畸变率。

最后需要说明的是,本文在界面形貌的形成机理及其随机过程中,都使用了正态分布,而实际情况需要进一步的微观界面形貌观察。此外,为了简化问题,本文忽略了主绝缘材料的电导非线性、炭黑颗粒与基料界面的电层特性、空间电荷等因素,在后续的研究中应逐步考虑,加以修正。

参考文献

Alden R T H, Qureshy F A .

HVDC—a review of applications and systems analysis methods

[J]. Canadian Electrical Engineering Journal, 1984,9(4):139-145.

DOI:10.1109/CEEJ.1984.6590969      URL     [本文引用: 1]

Ye Hanyu, Fechner Tobias, Lei Xianzhang , et al.

Review on HVDC cable terminations

[J]. High voltage, 2018,3(2):79-89.

DOI:10.1049/hve.2017.0144      URL     [本文引用: 1]

Hanley T L, Burford R P, Fleming R J , et al.

A general review of polymeric insulation for use in HVDC cables

[J]. IEEE Electrical Insulation Magazine, 2003,19(1):13-24.

[本文引用: 1]

Liu Y, Zhang S, Cao X , et al.

Simulation of electric field distribution in the XLPE insulation of a 320kV DC cable under steady and time-varying states

[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018,25(3):954-964.

DOI:10.1109/TDEI.2018.006973      URL     [本文引用: 1]

Du B X, Kong X X, Cui B , et al.

Improved ampacity of buried HVDC cable with high thermal conductivity LDPE/BN insulation

[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017,24(5):2667-2676.

DOI:10.1109/TDEI.2017.006452      URL     [本文引用: 1]

Le Roy S, Teyssèdre G, Laurent C .

Modelling space charge in a cable geometry

[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2016,23(4):2361-2367.

DOI:10.1109/TDEI.2016.7556514      URL     [本文引用: 1]

Sun Y, Li Z, Suo C, et al.

A simulation on space charge distribution caused by nonlinear conductivity in HVDC cable insulation

[C]. IEEE International Symposium on Electrical Insulating Materials, 2017: 126-129.

[本文引用: 1]

Mauseth F, Haugdal H .

Electric field simulations of high voltage DC extruded cable systems

[J]. IEEE Electrical Insulation Magazine, 2017,33(4):16-21.

[本文引用: 1]

Zhang S, Liu Y.

Simulation of space charge accumulation in LDPE under temperature gradient with temperature-dependent parameters

[C]. IEEE 12th International Conference on the Properties and Applications of Dielectric Materials, 2018: 1028-1032.

[本文引用: 1]

Hao Y, Chen Y, Yang L, et al.

Research on simplified equivalent method of 3D simulation model for temperature distribution of HVDC submarine cables

[C]. IEEE 1st International Conference on Electrical Materials and Power Equipment, 2017: 102-108.

[本文引用: 1]

Zhan Yunpeng, Chen George, Hao Miao, et al.

Thermal transient effects on space charge dynamics in HVDC extruded cable insulation

[C]. IEEE 12th International Conference on the Properties and Applications of Dielectric Materials, 2018: 1044-1047.

[本文引用: 1]

李旭兵, 李瑞 .

高压交联电缆三层共挤绝缘屏蔽合缝问题的解决

[J]. 电线电缆, 2007(3):42-43.

DOI:10.3390/s20010162      URL     PMID:31888053      [本文引用: 1]

AC arc faults are one of the most important causes of residential electrical wiring fires, which may produce extremely high temperatures and easily ignite surrounding combustible materials. The global interest in machine learning-based methods for arc fault diagnosis applications is increasing due to continuous challenges in efficiency and accuracy. In this paper, a temporal domain visualization convolutional neural network (TDV-CNN) methodology is proposed. The current transformer and high-speed data acquisition system are used to collect the current of a series of arc faults, then the signal is filtered by a digital filter and converted into a gray image in time sequence before being fed into TDV-CNN. Five different electric loads were selected for experimental validation with various signal characteristics, including vacuum cleaner, fluorescent lamp, dimmer, heater, and desktop computer. The experimental results confirm that the classification accuracy of the five loads' work states in the ten categories could reach 98.7% or even higher by adjusting parameters perfectly. The methodology is believed to be reliable for series arc detection with relatively high accuracy and also has important potential applications in other fault diagnosis fields.

Li Xubing, Li Rui .

Gap-closing of the insulation screen during the triple extrusion process of HV XLPE cables

[J]. Electric Wire & Cable, 2007(3):42-43.

DOI:10.3390/s20010162      URL     PMID:31888053      [本文引用: 1]

AC arc faults are one of the most important causes of residential electrical wiring fires, which may produce extremely high temperatures and easily ignite surrounding combustible materials. The global interest in machine learning-based methods for arc fault diagnosis applications is increasing due to continuous challenges in efficiency and accuracy. In this paper, a temporal domain visualization convolutional neural network (TDV-CNN) methodology is proposed. The current transformer and high-speed data acquisition system are used to collect the current of a series of arc faults, then the signal is filtered by a digital filter and converted into a gray image in time sequence before being fed into TDV-CNN. Five different electric loads were selected for experimental validation with various signal characteristics, including vacuum cleaner, fluorescent lamp, dimmer, heater, and desktop computer. The experimental results confirm that the classification accuracy of the five loads' work states in the ten categories could reach 98.7% or even higher by adjusting parameters perfectly. The methodology is believed to be reliable for series arc detection with relatively high accuracy and also has important potential applications in other fault diagnosis fields.

欧阳本红, 华明, 邓显波 .

高压交联电缆材料及工艺发展综述

[J]. 绝缘材料, 2016,49(7):1-6.

[本文引用: 1]

Ouyang Benhong, Hua Ming, Deng Xianbo .

A review about development of HV XLPE cable materials and processes

[J]. Insulating Materials, 2016,49(7):1-6.

[本文引用: 1]

鄢薇, 甄建, 薛志刚 .可交联

PE 电缆用半导电屏蔽料开发现状

[J]. 合成树脂及塑料, 2012(4):75-79.

[本文引用: 1]

Yan Wei, Zhen Jian, Xue Zhigang . Development situations of semiconducting XLPE cable shielding material[J]. China Synthetic Resin and Plastics, 2012(4):75-79.

[本文引用: 1]

刘英, 王乐, 王磊 , 等.

从缺陷影响看高压 XLPE 电缆绝缘减薄的必要性

[J]. 高电压技术, 2006,32(7):29-32.

[本文引用: 1]

Liu Ying, Wang Le, Wang Lei , et al.

Necessity of reducing the insulation thickness of HV XLPE cables from the defect point of view

[J]. High Voltage Engineering, 2006,32(7):29-32.

[本文引用: 1]

/

〈 〉