1 引言
永磁同步电机(Permanent Magnet Synchronous Machine,PMSM)因其结构简单、运行可靠;体积小、质量轻;损耗小、效率高等显著优点,被广泛应用在航空航天、国防和工农业生产等领域[1]。拥有准确的电机参数是实现永磁同步电机高性能控制系统的前提条件。永磁同步电机高性能控制系统广泛应用矢量控制技术,该控制系统设计用到的主要电机参数有定子电阻Rs,同步旋转坐标系下的交直轴电感Ld、Lq,转子永磁体磁链Ψf等。定子电阻通过施加两段幅值不同的直流定子电流就可以较准确辨识,而转子磁链可以通过电机额定参数计算。辨识交直轴电感参数的传统方法需要转子以恒速旋转,文献[2,3,4,5,6]中介绍了在电机恒速旋转的条件下辨识电机电感的在线辨识方法,但这些方法大都需要冗繁的计算,编程实现难度很大。文献[7,8]中使用的基于信号处理法和系统识别理论的辨识方法,简单易实现,但仍需电机恒速运转。
一般情况下,控制系统需要在起动电机之前获取电机参数,以得到优越的起动动态性能;另外,由于机械连接,很多情况下电机正式工作前不允许转子转动。这些情况必须使用转子静止式的参数辨识策略。因此,对于将电机驱动系统产品化的变频器与伺服电机生产企业,解决电机参数辨识静止化的问题刻不容缓。
本文提出一种转子静止条件下辨识永磁同步电机电感的方法。首先寻找转子dq轴初始位置,不需要转子位置拉入。模仿转子位置检测过程中给定子施加高频电压信号的方法,以PMSM矢量控制系统为基础,通过给定子施加类似的高频正弦电压信号激励出正弦电流响应,利用电压重构技术和DFT算法对电压电流信号处理,消除由死区带来的电压偏差,削弱空间谐波的影响,实现电感的精确辨识。该方法特别适合于内置式永磁同步电机和同步磁阻电机等由于气隙磁场不均匀造成电流谐波含量较高的电机。
2 同步旋转坐标系数学模型
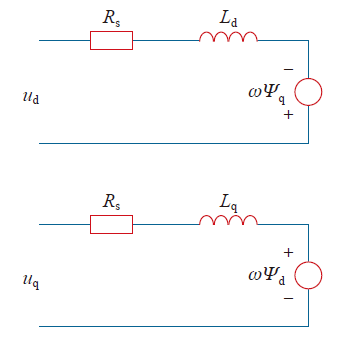
图1
首先假设:①忽略电动机铁心的饱和;②不计电动机的铁损;③电机三相绕组对称,在空间相差120°电角度,所产生的磁动势沿气隙按正弦规律分布。得到电机dq坐标下的电压方程
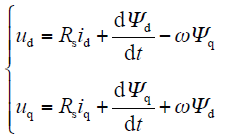
磁链方程为
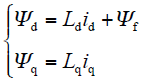
转矩方程为
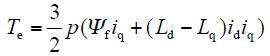
运动方程为
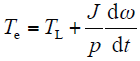
式中,id、iq为定子合成电流在d、q轴上的分量;Ld、Lq为定子在d、q轴上的等效电枢电感;p为极对数;TL为总负载转矩;J为总转动惯量。
3 电感参数辨识
本论文提出的电感参数辨识策略可分为三部分:转子位置检测、直轴电感辨识和交轴电感辨识。
3.1 转子初始位置检测
永磁同步电机转子初始位置信息不仅是参数辨识的需求,更是电机正常起动运行必备条件。简单的将转子磁极拉到d轴,可以满足电机起动的需要,但不能满足本文转子静止的要求。
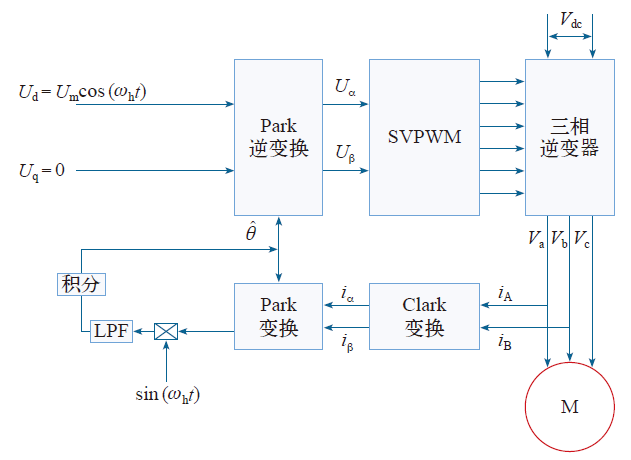
本文使用一种无位置传感器转子初始位置检测方法,首先在估算位置下的同步旋转坐标系中注入高频正弦电压信号,通过闭环调节得出转子位置初次估算值,再利用不同磁极下直轴等效电路时间常数不同的特性,判断出d轴正方向,结合初次估算值,得到正确的初始位置信息[10]。
图1为永磁同步电机dq轴电机等效模型。电机静止时,转速ω = 0电机在dq轴上相当于RL串联负载。电压方程简化为
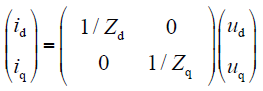
式中,Zd、Zq为交直轴阻抗。
首先,假定位置估算在与定子U相绕组电角度为0处,施加d轴高频正弦电压形式见式(6),若估算的位置不正确,那么q轴会有电流响应$\hat{i}_{q}\ne 0$,$\hat{i}_{q}$形式见式(7)。
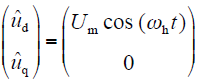
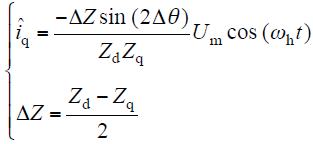
对式(7)进行必要的变换,有
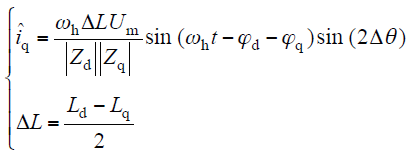
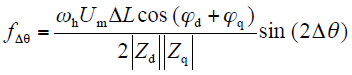
图2
表1 不同区间位置收敛值
Tab.1
| 转子实际位置θ | 估算位置收敛值 |
|---|---|
| θ∈(-π,-π/2) | θ + π |
| θ∈(-π/2,0) | θ |
| θ∈(0,π/2) | θ |
| θ∈(π/2,π) | θ - π |
3.2 转子静止式辨识
根据上一节中转子初始位置检测的策略,可以得到d轴正方向的电角度位置θ。电机转子静止时,该角度保持不变,d轴与两相静止坐标系(αβ坐标系)α轴的夹角成为已知条件。不再需要转子位置拉入步骤,避免了转子发生旋转位移。
3.2.1 辨识原理
假设前面的转子位置检测结果为θ,向电机打入形如式(6)的交流电压,只是幅值和频率与前者不同,如下
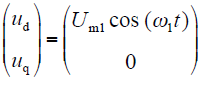
响应电流形式
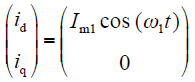
由式(5)计算d轴电抗Zd = Ud/Id 。其中,Ud、Id均为有效值。只要获得d轴给定交流电压和响应电流的有效值,由式(12)可计算出Ld的值。
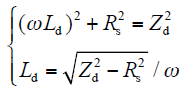
在数字控制系统中,对电流的采样值为离散量,不能直接得到电流有效值。本文采用了离散傅里叶算法(DFT)辅助电流有效值的获取。DFT算法的思想是:对电流的一个周期N次采样,只要采样满足采样定理,根据N次的采样值,可直接得到各次谐波分量的实部和虚部,进而计算出相应量的有效值。
对电流一个周期内进行N次采样,基波电流实部a1和虚部b1为

电流基波有效值为
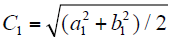
定子三相电流检测值经过3s/2s变换和2s/2r变换,再经过上述DFT算法,计算出d轴电流基波分量的有效值Id。
由于输出电压为PWM波,等幅不等宽,一般的变频器中没有成本昂贵的电压传感器,不能够直接测得输出电压的大小。由于死区等因素的影响,给定电压和实际输出电压之间存在偏差。为了减小偏差的影响,本文利用电压重构技术,首先还原输出电压为连续量,补偿死区的影响,然后根据DFT算法求出其有效值。
s1、s2、s3分别为上桥臂开关管在一个开关周期TS内的给定瞬时相电压占空比[13]。三相电压可以表示为
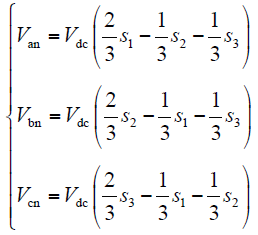
由死区引起的电压偏差量为[13]

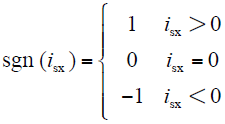
式中,Td为死区时间;fs为开关时间;Udc为直流侧电压;isx为定子a、b、c相电流。
通过幅值不变的坐标变换,可以推导出dq坐标下的直轴电压和交轴电压。对重构出来的d轴电压使用DFT算法,同样也获得基波分量有效值Ud,由式Zd = Ud/Id与式(12)计算出Ld。
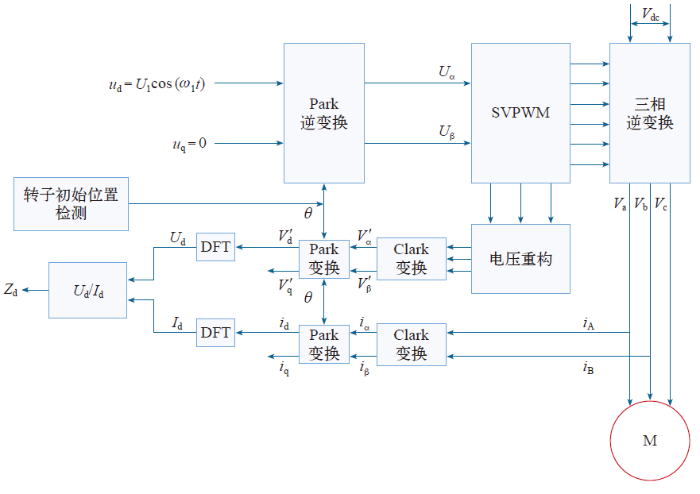
由于只使用了基波分量,电机本身结构等因素所导致的空间谐波对辨识结果的影响将被大大削弱,使本方法比其他辨识策略有更好的精确性,特别适用IPM电机。图3为Ld辨识过程系统框图。
图3
q轴的电感辨识与d轴类似,向电机施加的电压形式见式(18),响应电流形式见式(19)。
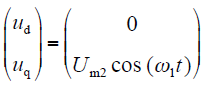
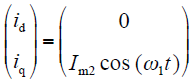
使用相同的电压重构技术和DFT技术,使用的q轴电压和电流基波分量有效值计算q轴电感Lq。
3.2.2 运行状态分析
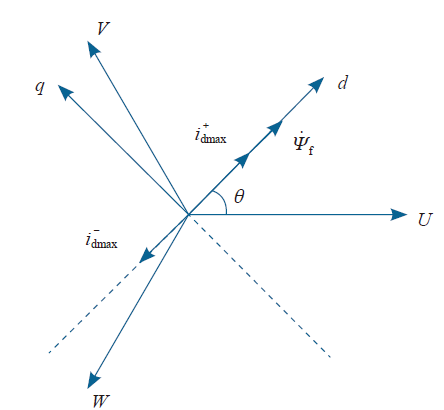
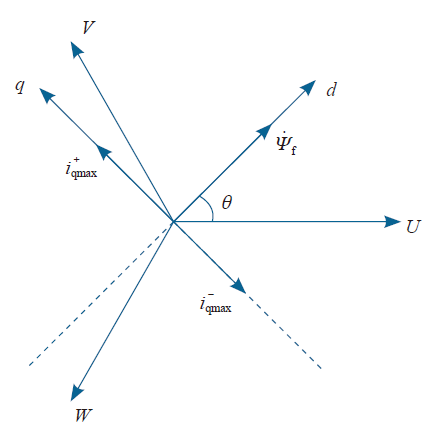
假设某初始状态下d轴与U轴夹角为θ。图4、图5分别为d轴和q轴电感辨识过程中的矢量图。图4中,只有d轴电流分量、幅值大小按正弦规律在正负反复连续变化,且与转子磁链同轴,d轴磁链矢量与转子磁链矢量亦同轴,定转子磁场之间无力的相互作用。图5中,只有q轴电流分量,幅值大小同样按照正弦规律变化。q轴磁链因此也在q轴与电流同规律变化,并与转子永磁磁链呈90°电角度,dq轴磁场之间产生非常强烈的磁力作用,使电机转子有发生转动的趋势。q轴磁链并不是一个旋转的磁链,而是一个正负之间连续脉动的磁链,所以转子不会发生旋转,而是会产生振动。如果施加的交流电压频率较低,电机转子会有较大振幅,并且产生大的振动噪声。为避免转子发生振动旋转位移和减弱噪声,q轴交流电压的频率必须较高,工程上可以使用500Hz。
图4
图5
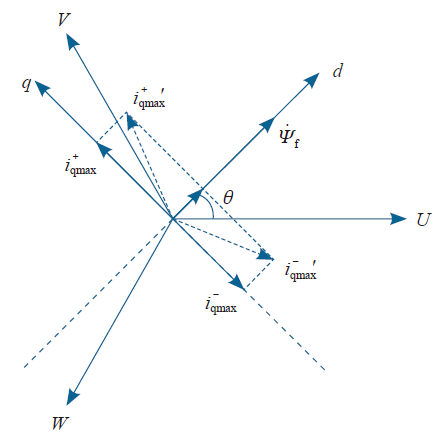
单相高频注入的过程中,可能由于机械振动等原因使转子偏离原位置,这种情况在空载条件下较常见。在d轴方向上增加小直流分量可维持转子位置固定。增加d轴直流分量后,d轴电感辨识过程中的电流合成矢量方向不变,只向d轴正方向偏移一个直流量。q轴电感辨识过程中各矢量关系如图6所示,可以看出,增加直流分量后,电流合成矢量的方向变化范围缩小,不仅能够锁住转子位置,还可以起到降低振动噪声的作用。
图6
由式(10)和式(18)得出,带有d轴小直流分量的电压给定为:
d轴辨识过程
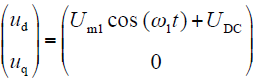
q轴辨识过程

利用坐标变换并结合式(11)和式(19),得到d、q辨识过程中三相定子电流波形分别满足式(22)和式(23)。
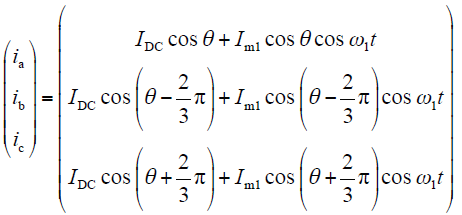
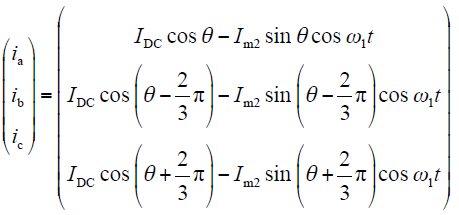
4 实验结果
本文使用瑞萨单片机为主芯片搭建了永磁同步电机控制系统实验平台,包括三相不控整流、三相桥式电压源型逆变电路以及采样、调理等电路。以SVPWM控制技术为基础实现了PMSM的最大转矩电流比控制(Maximum Torque per Ampere Control)。
为验证所提出的电感辨识策略的有效性和精确性,对3台不同品牌的永磁同步电机(PM1:登奇0.75kW;PM2:士林3.7kW;PM3:朗高7.5kW)进行了参数辨识。其中前两台为SPM类型PM,标称参数Ld = Lq。3台PM的电感参数标称值见表2。
表2 电机标称参数
Tab.2
| 电机编号 | PM1 | PM2 | PM3 |
|---|---|---|---|
| Ld /mH | 33.25 | 1.33 | 5.73 |
| Lq /mH | 33.25 | 1.33 | 10.38 |
实验中为保证正确性和降低噪声,选择500Hz输出电流频率,10kHz载波。表3为本文方案的辨识实验结果,可见辨识结果与电机名牌标称值不完全一致。这是由温升、磁路饱和等因素导致的,也正是需要参数辨识的一个原因。
表3 电机参数辨识结果
Tab.3
| 电机编号 | PM1 | PM2 | PM3 |
|---|---|---|---|
| Ld /mH | 30.83 | 1.43 | 5.27 |
| Lq /mH | 39.54 | 1.52 | 9.83 |
图7
图7
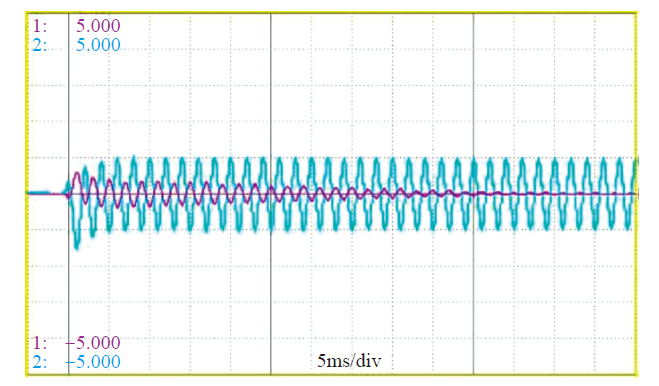
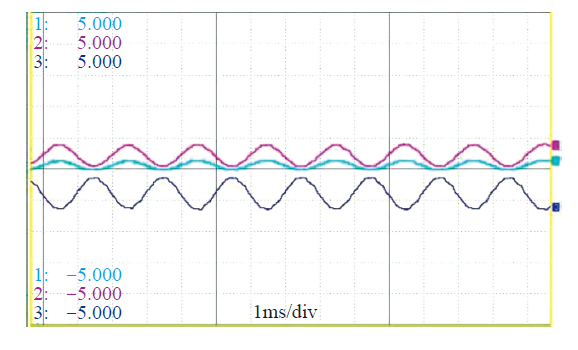
转子初始位置检测第一阶段电流波形
Fig.7
Stator current during first stage of initial rotor position detection
图8
图8
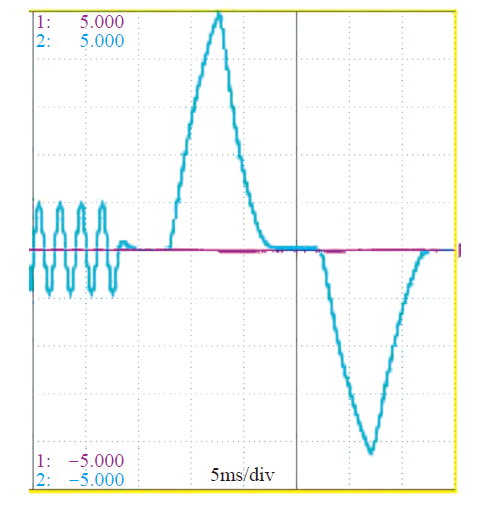
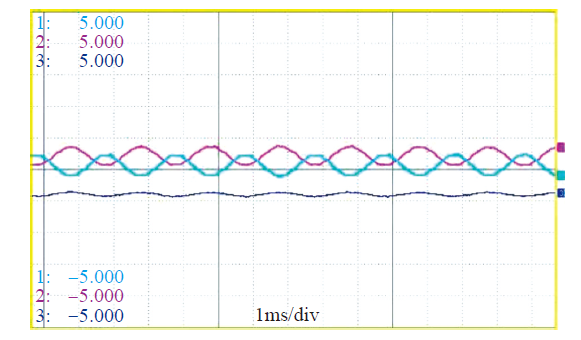
转子初始位置检测第二阶段电流波形
Fig.8
Stator current during second stage of initial rotor position detection
图9
图10
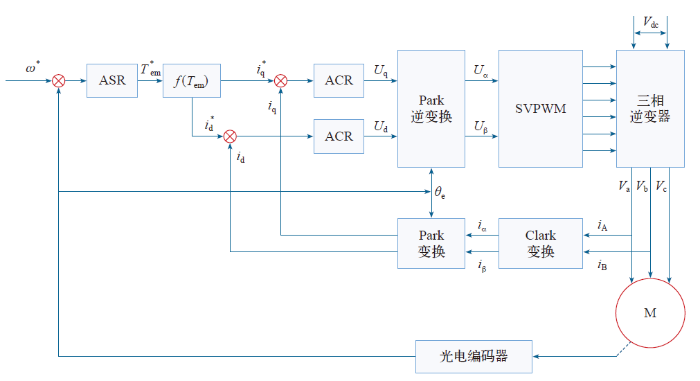
以转子静止式辨识方法得到的电机电感参数为基础,结合PI参数整定,建立PMSM最大转矩电流比控制系统。图11为MTPA控制系统框图。
图11
为确定参数的准确性,分别测试该系统的起动特性,加卸载特性和转矩特性。使用朗高7.5kW内置式PM电机进行上述动态性能测试。该电机各额定标称参数见表4。
表4 朗高7.5kW电机参数
Tab.4
| 额定功率 /kW | 额定电压 /V | 额定电流 /A | 额定频率 /Hz | 额定转矩 /N·m | 极数 |
|---|---|---|---|---|---|
| 7.5 | 380 | 15 | 100 | 48 | 8 |
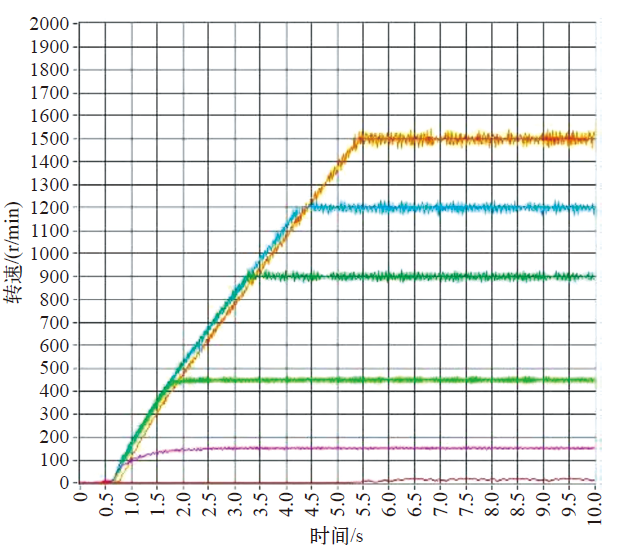
图12为起动特性测试结果。图中各条曲线由下至上分别为电机以满载起动并匀加速至1Hz、10Hz、30Hz、60Hz、80Hz和100Hz。从图中可以看到,电机加速过程平稳,加速度基本恒定,系统起动性能优越。
图12
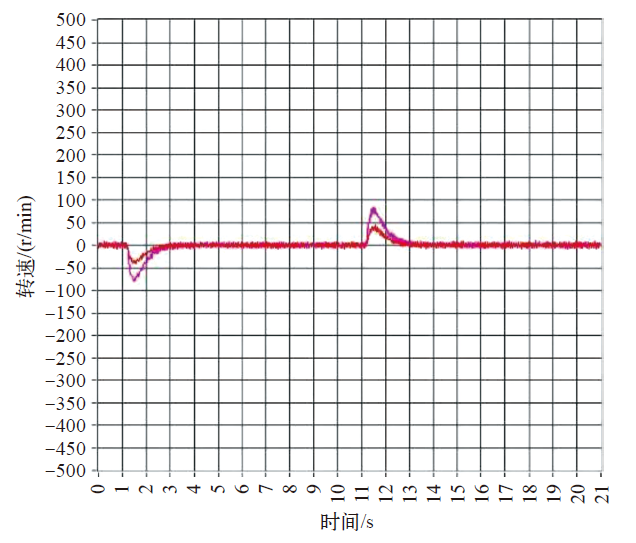
图13为加卸载特性测试结果。电机以50Hz恒速运行。图中两条曲线分别表示突加、突减50%额定负载(波动较小者)与突加、突减100%额定负载(波动较大者)电机转速的变化趋势。可以看到,加卸载过程中电机转速波动幅度较小,加卸载特性优越。
图13
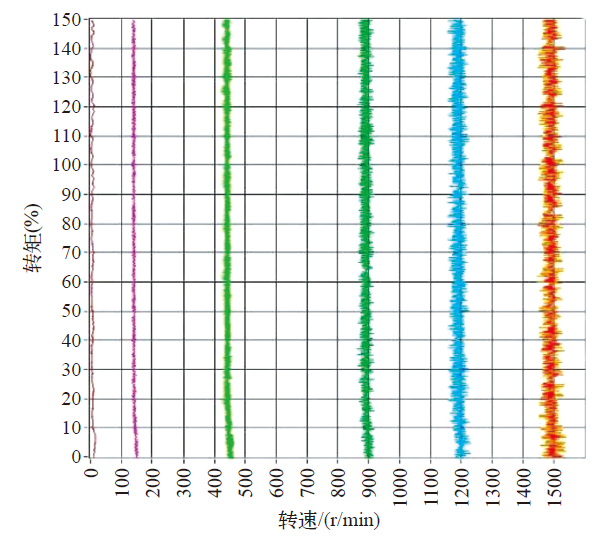
图14为转矩特性测试结果。图中6条曲线从左至右分别为电机以1Hz、10Hz、30Hz、60Hz、80Hz和100Hz运转时由空载均匀加载至150%额定负载的过程。可以看到各条曲线没有明显向左倾斜,说明在负载增加过程中电机转速稳定好,系统转矩特性优越。
图14
通过测试确定了该控制系统动态性能优越,说明本文提出的参数辨识方法具有足够的精确性。
5 结论
本文结合转子初始位置检测使用一种新颖的永磁同步电机电感参数辨识策略,在转子完全静止的条件下实现了永磁同步电机交直轴电感的精确辨识。其转子完全静止的特点使变频控制系统能够应用于电机正式起动前不允许旋转的众多场合。该方法基于永磁同步电机的变频控制平台,不需要额外的硬件电路与测量设备,方便实用。DFT算法和电压重构技术大大削弱了谐波和死区对电流电压值计算的影响,显著提高了辨识精度,使本文策略尤其适用于谐波含量较高的IPM电机。
参考文献
内嵌式永磁同步电动机电感参数辨识
[J].
Inductance parameter identification of interior permanent magnet synchronous motor
[J].
Determination of parameters for internal permanent magnet synchronous motors
[C].
基于系统识别理论在线参数辨识的永磁同步电动机无传感器控制
[J].
Sensorless control of permanent-magnet synchronous motors using online parameter identfication based on system identification theory
[J].
Identification of machine parameters of a synchronous motor
[C].
永磁同步电机电感参数测量系统研究
[J].
Research on inductance parameter measurement system for permanent magnet synchrinous motor
[J].
内置式永磁同步电机交、直轴电枢反应电抗的准确计算
[J].
Accurate calculation of quadrature-axis and direct-axis armature reaction reactance for a interior permanent magnet synchronous machine
[J].
转子磁钢表贴式永磁同步电机转子初始位置检测
[J].
Initial rotor position detection of surface mounted permanent magnet synchronous motor
[J].
两种智能算法在感应电动机参数辨识中的应用
[J].
三相电压源逆变器输出电压重构技术的研究
[J].
Research on the reconstruction of output voltage in three-Phase voltage source inverter
[J].