1 引言
目前,关于架空导线的载流温升模型的研究发展已较为成熟,主要可分为标准模型、数值模拟模型及热路模型。其中,标准模型主要指IEC61597—1995标准模型[4]和IEEE738—2006标准模型[5],可用于计算不同气象、载流条件下的导线运行温度,以确定线路载流量。而IEEE模型还可实时计算导线温度动态过程,相比IEC模型更具实用价值[6],至今仍在不断完善并已实际应用于动态增容技术中。基于数值传热学理论的数值模型将描述导线热动态过程的偏微分在空间及时间上离散求解,来模拟导线的温度场[7,8,9]。但该模型计算量极大,难以实现实际应用。热路模型是将热电类比理论引入IEEE模型,通过电路计算有效地简化了复杂的传热计算[10,11,12]。相比IEEE模型,热路模型能够利用更少的参数反推导线热动态特性,可有效运用于线路动态增容中。
为此,本文以ACCC导线为对象,在热平衡原理和热电类比理论的基础上,建立针对ACCC导线的载流温升模型,并通过粒子群优化算法,提出了模型参数的辨识方法,为ACCC导线的线路的动态增容和安全运行提供必要依据。
2 高压ACCC导线载流温升模型
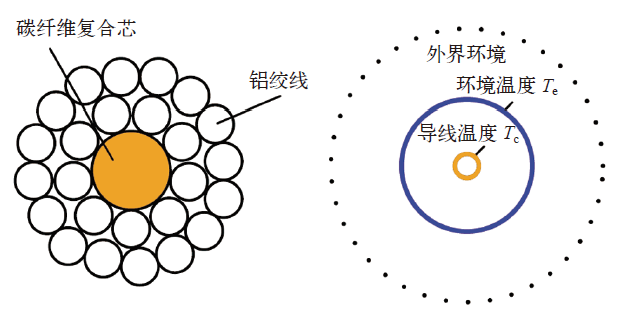
ACCC导线的截面图和物理模型如图1所示。在架空导线运行过程中,导线受日照、环境温度和风速等环境因素影响而与外界环境发生热交换。因此,根据热平衡原理,可将ACCC导线的热动态过程描述为
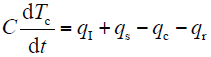
图1
图1
国产ACCC的截面图及物理模型
Fig.1
The section and physical model of domestic ACCC conductor
式中,t为时间;Tc为导线温度;C为导线热容;qI = I2R(Tc)为导线的自身发热功率;R(Tc)为导线温度为Tc时的导线交流电阻;qs为日照吸热功率;qc为对流散热功率;qr为辐射散热功率。
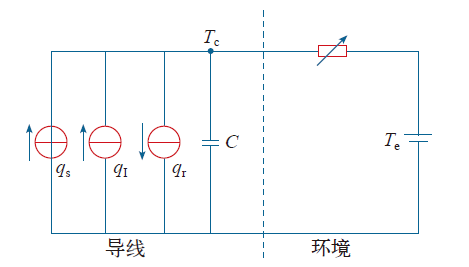
根据热电类比理论,ACCC导线的热路模型可表示为图2所示的电路模型,热路模型可改写为
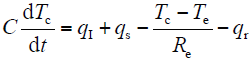
图2
线路的载流量可表达为
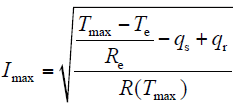
式中,Re为导线表面与环境之间的等效环境热阻;Tmax为导线最大允许运行温度。有研究表明,ACCC导线持续运行温度高达160℃,短时运行温度可超200℃[19]。
热路模型中各参数计算如下
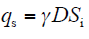
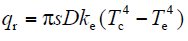
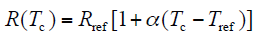
式中,α为电阻温度系数;Rref为参考温度Tref时的导线交流电阻;Tref一般取20℃;D为导线外径;Si为日照强度;s为斯蒂芬–玻尔兹曼常数;γ和ke分别为导线表面材料的吸收率和发射率,工程中通常取为0.5。
3 热路模型参数的粒子群辨识
在上述提出的热路模型中,模型参数C、Rref及α的确定还缺乏理论依据。这主要由两方面原因引起:其一,ACCC导线线芯为柱状碳纤维复合材料,其热容难以直接根据理论计算得到。其二,由于绝缘树脂的包裹,线芯具有不导电、不导磁的物理特性,消除了导线的涡流磁损。因此,与传统架空导线不同,ACCC导线交流电阻中由涡流和磁滞引起的电阻增量可以忽略,式(6)中的Rref和α也难以参考传统架空导线计算。
由文献[20]可知,环境热阻Re本质上与导线及环境之间的温差有关。考虑到指数函数能够描述变量的线性或非线性变化,本文将环境热阻表示为
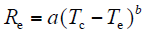
式中,a为比例因子,与导线线径及空气密度有关;b为指数因子。a和b均为未知量,需由辨识方法获得。
为得到上述模型参数,需首先建立相应目标函数。设时刻k + 1时,导线温度为Tc(k + 1)。从热路模型的微分形式上可看出,Tc(k + 1)可由k + 1时刻前的输入量及初始边界条件推得。那么,将式(4)~式(7)带入热路模型,并进行时间上的离散,可推得k + 1时刻导线温度Tc(k + 1)函数为
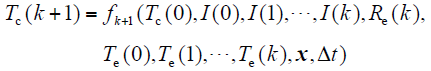
式中,Δt为离散步长。x为辨识参数向量
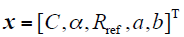
由此,得到热路模型参数辨识的目标函数
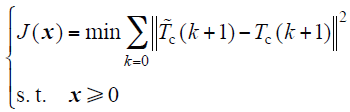
式中,$\widetilde{T}_{c}(k+1)$为k + 1时刻导线的实测温度。
由于本文提出的热路模型待辨识参数较多,且为非线性优化问题,需要良好的全局寻优能力,本文采用粒子群优化算法对目标函数进行求解。
首先定义搜索种群G
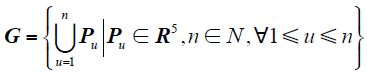
式中,R5为由待辨识参数构成的五维搜索空间;Pu为搜索粒子。
种群初始化完成后,将每个粒子的位置向量代入目标函数,计算目标函数适应度值,并筛选出最优粒子与最优适应度值。之后,更新粒子位置与速度向量,进行下一轮寻优,第s次寻优的更新公式为
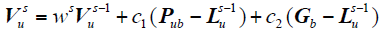
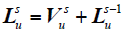
式中,Pub为粒子最优解;Gb为种群最优解;c1、c2为学习因子,分别代表粒子向自身和其他粒子的学习能力;ws为权重系数;Lu = [lu1lu2lu3lu4lu5]为粒子的位置向量,代表辨识参数值结果,Vu = [vu1vu2vu3vu4vu5]为粒子的速度向量,表示粒子向下一位置搜索的方向。
利用粒子群优化算法,经过若干轮寻优过程后,可实现上述目标函数的求解,完成ACCC导线热路模型的建立。
4 实验验证及结果分析
4.1 实验平台
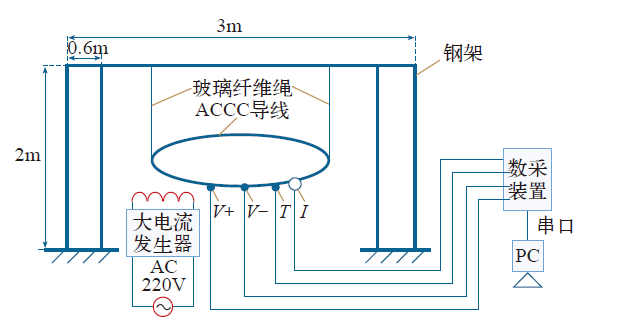
为辨识求解热路模型参数,并验证其正确性和精度,设计了如图3所示的ACCC导线载流温升实验平台。
图3
图3
ACCC导线载流温升实验平台示意图
Fig.3
The schematic diagram of temperature rise experiment platform for current-carrying ACCC conductor
实验平台主要包括:钢架、实验导线、大电流发生器、温度探头、差分电压探头、霍尔电流互感器、数采装置及PC机构成。钢架由两个侧架和一根横梁组成,横梁上悬挂有玻璃纤维绳来架设实验导线。玻璃纤维绳可耐高温、导热系数小,使得架设材料对导线导热的影响最小。本文采用硅谷化工生产的ACCC导线作为实验对象,其相关参数见表1。
表1 ACCC-240/35参数
Tab.1
| 参数名 | 参数值 |
|---|---|
| 规格 | ACCC-240/35 |
| 导线长度/m | 5 |
| 层数 | 2 |
| 铝股数 | 25 |
| 芯线直径/mm | 7.5 |
| 线径/mm | 21.7 |
| 20℃直流电阻/(Ω·km-1) | 0.1209 |
| 允许连续使用温度/℃ | 160 |
实验平台放置于封闭的室内,室内空气流速小于0.1m/s,属自然对流,温度和湿度在实验阶段近似不变。实验时,大电流发生器将电流耦合至ACCC导线。同时,导线实时运行温度、环境温度及导线电流通过温度探头及霍尔电流互感器由数采装置采集以0.5s为周期上传至后台PC数据库存储起来。
4.2 结果及分析
为获取较为全面的导线温升过程甚至过载时的温升,实验选取400~1 000A,间隔100A的电流值作为加载电流。
将实验结果带入目标函数,并利用粒子群优化算法辨识求解得到ACCC导线热路模型参数见表2。
表2 模型参数辨识结果
Tab.2
| 辨识参数 | 辨识结果 |
|---|---|
| 热容C/(J·K-1·m-1) | 4087.7 |
| 交流电阻温度系数α | 0.0030 |
| 20℃时的导线交流电阻Rref/(Ω·km-1) | 0.1559 |
| 环境热阻系数a | 1.6024 |
| 环境热阻系数b | 0.1782 |
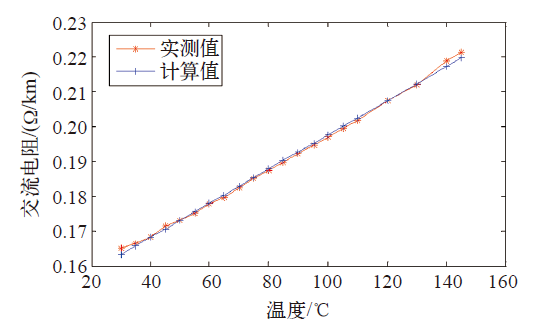
首先,验证交流电阻参数的有效性。将辨识结果带入式(5),计算出不同导线温度下的交流电阻,与通过矢量电流电压法测得的交流电阻值对比,如图4所示。其最大误差仅为1.2%,表明参数和Rref的辨识结果具有较高的精度。
图4
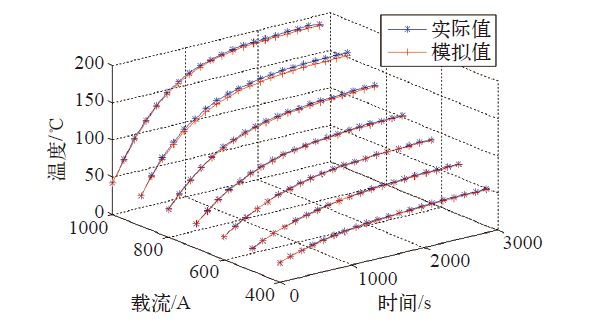
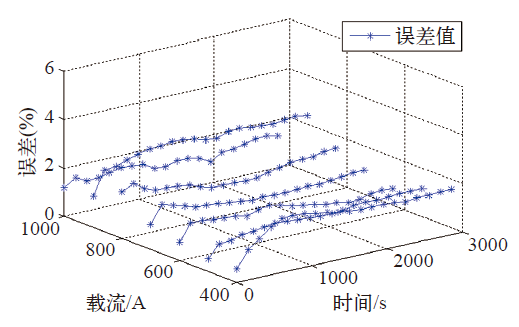
图5
图5
不同电流等级下的导线室内温升实测与模拟结果
Fig.5
The measured and simulation results of conductor temperature rise with different current in the indoor condition
图6
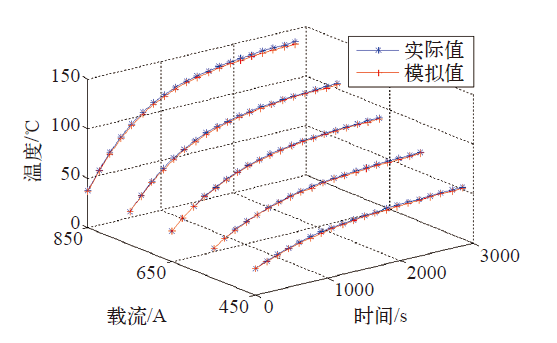
图7
图7
增补加载电流下的导线温升实测与模拟结果
Fig.7
The measured and simulation results of conductor temperature rise for added current
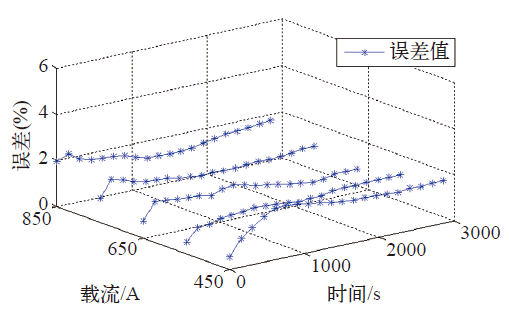
图8
图8
增补加载电流下的导线模拟结果的相对误差
Fig.8
The relative error of simulation result for added current
5 结论
本文提出了基于粒子群优化算法辨识的高压ACCC导线载流温升模型,通过实验验证了辨识计算方法的可行性和模型的精确性,确定了模型各参数的具体计算方法,并得到如下结论:
(1)基于粒子群参数辨识的辨识方法可有效确定ACCC导线载流温升模型中的电参数及热参数,为导线热动态过程的计算提供必要依据。
(2)实验结果与计算结果对比表明,自然对流条件下,ACCC导线载流温升模型具有较高的精度,可准确反映导线的温升过程,为复杂气象条件下的导线载流温升模型提供了理论基础。
参考文献
输电线路实时增容技术的理论计算与应用研究
[J].
Theoretical calculation and capacity-increase application study on real-time of transmission lines
[J].
输电线路实时动态增容的可行性研究
[J].
Study on real-time dynamic capacity-increase of transmission line
[J].
System impacts of temperature-dependent transmission line models
[J].
Overhead electrical conductors-calculation methods for stranded bare conductors
[S].
IEEE Standard for calculating the current-temperature of bare overhead conductors
[S].
输电线路摩尔根载流量简化公式的初步研究
[J].
Preliminary study on morgan transmission capacity simplified formula of transmission lines
[J].
Theoretical model for temperature gradients within bare overhead conductors
[J].
The radial temperature distribution and effective radial thermal conductivity in bare solid and stranded conductors
[J].
Radial temperature distribution in ACSR conductors applying finite elements
[J].
架空导线动态增容的热路法暂态模型
[J].
A transient model for overhead transmission line dynamic rating based on thermal circuit method
[J].
架空导线动态增容的热路法稳态模型
[J].
Steady-state model of thermal circuit method for dynamie overhead lines rating
[J].
Harmonic analysis of dynamic thermal problems in high voltage overhead transmission lines and buried cables
[J].
A composite core conductor for low sag at high temperatures
[J].
Failure prediction analysis of an ACCC conductor subjected to thermal and mechanical stresses
[J].
国内碳纤维复合芯导线的研究和应用综述
[J].
Research and application overview of ACCC conductor in china
[J].
High-temperature conductors: a solution in the uprating of overhead transmission lines
[M].
Field testing of ACCR conductor
[J].
基于脉动参数热路模型的架空线路动态增容风险评估
[J].
Risk assessment of dynamic overhead lines rating based on thermal circuit model considering pulsating characteristic of parameters
[J].