电气工程学报, 2017, 12(5): 1-7 doi: 10.11985/2017.05.001

分数槽永磁电机的多物理场耦合分析

杨凯, 颜建虎, 张尚坤

南京理工大学自动化学院 南京 210094

Multi-Physics Filed Coupling Analysis of Fractional Slot Permanent Magnet Machine

Yang Kai, Yan Jianhu, Zhang Shangkun

Nanjing University of Science and Technology Nanjing 210094 China

收稿日期: 2016-06-2   网络出版日期: 2017-05-25

基金资助: 国家自然科学基金项目.  51407094
江苏省自然科学基金项目.  BK20140785

Received: 2016-06-2   Online: 2017-05-25

作者简介 About authors

杨 凯 男 1992年生,硕士研究生,研究方向为电机多物理场计算。

颜建虎 男 1983年生,博士,讲师,研究方向为新型永磁电机设计与控制。

摘要

由于电机的运行状态与特性与其电、磁、热等物理场直接相关,因此对电机进行多物理场耦合分析至关重要。本文利用三维有限元法对分数槽永磁电机在运行时的磁场分布进行分析计算,并由磁场分析结果计算出各部分损耗情况,将各部分损耗作为电机运行时的热源,对电机的温度场进行仿真分析,得到电机的温度分布情况。并在此基础上,对一台样机进行实验分析,实验结果与仿真结果一致。从而验证了对该电机的多物理场耦合分析方法的有效性,为后续的电机结构优化奠定了理论基础。

关键词： 永磁电机 ; 分数槽 ; 损耗 ; 多物理场 ; 有限元法

Abstract

Due to the running status and characteristics of the electric machines are directly related to its electrical, magnetic, thermal and other physical fields, multiple physical field coupling analysis is of great importance. In this paper, 3D finite element method is used to research on magnetic field distribution when the fractional slot permanent magnet machine running, and get loss values by magnetic field analysis. Taking each part of the loss as a heat source of the electric machine in the simulation analysis of temperature field of permanent magnet machine and got the temperature distribution of the machine. Then a prototype machine is used to experiment based on this. The validity of the multiple physical field coupling analysis method is confirmed through the comparison of the experimental results with the simulation results, laid a theoretical basis for the subsequent electric machine structure optimization.

Keywords： Permanent magnet machine ; fractional slot ; loss ; multi-physics field ; finite element method

PDF (4615KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杨凯, 颜建虎, 张尚坤. 分数槽永磁电机的多物理场耦合分析. 电气工程学报[J], 2017, 12(5): 1-7 doi:10.11985/2017.05.001

Yang Kai. Multi-Physics Filed Coupling Analysis of Fractional Slot Permanent Magnet Machine. Journal of Electrical Engineering[J], 2017, 12(5): 1-7 doi:10.11985/2017.05.001

1 引言

与传统的电励磁电机相比,稀土永磁电机具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高、电机的形状和尺寸灵活多样等优点,因而广泛应用于航空航天、国防、工农业生产和日常生活等领域。对电机磁场的分析和计算是电机设计的重要环节,然而,永磁电机在运行过程中的温升对运行状态产生较大影响,使永磁体过热而产生不可逆退磁。所以在永磁电机设计和分析中对其热场的分析和计算具有重要的意义[1,2]。

目前对电机物理场的计算和分析主要采用有限元法,分析过程易于实现标准化,可得到通用的计算程序且有较高的计算精度,因此特别适合求解电机这类边界形状复杂、存在材料非线性的磁场问题。要计算电机内的温度场,首先应准确地计算电机内各部分的损耗,确定电机的热源。永磁电机损耗主要包括铁耗、定子绕组铜耗、机械损耗、转子的涡流损耗以及未计入上述损耗的其他附加损耗,这些损耗会转变成热能并经电机冷却系统带走,同时使电机各部件温度升高。因此对永磁电机损耗的精确计算对准备计算和分析电机温度场有着重要意义[3,4]。

目前,国内外采用的电机热计算方法主要有简化公式法、热网络法、温度场法、参数辨识法和基于运行状态参量的电机温度模型[5,6,7]。哈尔滨理工大学的李伟力等人对大型电机定子三维流体场及其对温度场的影响和大型同步发电机定子多元流场与表面散热系数之间的关系进行了数值计算与分析,并将电机内的流体场与温度场进行耦合计算[8]。沈阳工业大学的王凤翔等人基于磁场有限元和3D流体场分析对高速永磁电机进行了损耗计算,并基于流固耦合分析对电机的温升进行了计算[9]。沈阳工业大学的唐任远等人采用三维有限元法对永磁风力发电机进行了三维温度场的计算与分析,验证了采取热源、绕组等效导热系数的计算方法的可行性[10]。悉尼科技大学的D. G. Dorrell等人采用2D有限元分析方法研究了高速无刷永磁电机线圈中的趋肤效应和临近效应[11]。瑞典皇家理工学院的O. Aglen等人对高速发电机进行了损耗计算和热分析,结果表明在转子中加入铜网可以降低损耗值[12]。芬兰阿尔托大学的Z. Kolondzovski采用2D-3D数值相结合的方法对高速永磁电机进行了热分析并采用有限元转子动力学建模的方法对电机进行了机械性能的分析[13]。

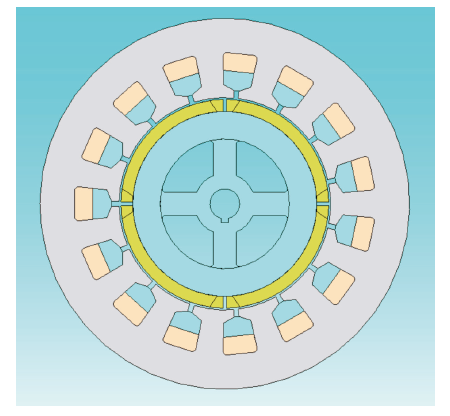
本文以一台额定转速为1 500r/min的4极15槽的永磁同步电机为例,采用三维有限元法对电机的磁场、损耗和温度场进行计算,并对电机在稳定运行时的磁场和温度场进行了分析。在此基础上与样机进行了实验对比,为后续电机的结构优化设计和分析奠定了理论基础。

2 永磁电机的磁场分析

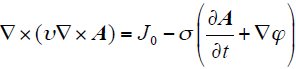
对于永磁电机来说,其磁场的准确计算分析是研究电机性能的重要环节,通常采用磁路法对电机进行简化计算,然而计算精度较差,且无法解决电机内部所有的问题。因此,在进行永磁电机磁场分析时,通常采用有限元法来进行分析和计算。考虑到对电机损耗的准确分析,三维有限元法成为主要的计算和分析方式,用三维有限元分析磁场和涡流场,主要基于A-ϕ法,其基本方程为[14,15]

式中,A为磁矢量位;ϕ为电标量位;σ为电导率;υ为磁阻率;J0为线圈的电流密度。

3 永磁电机温度场分析

3.1 温度场理论分析

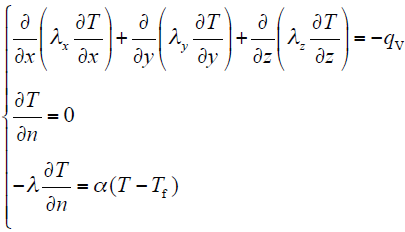
根据传热学的基本理论,在直角坐标系下,电机内的稳态温度场求解可归结为如下的边值问题[9,10]

式中,λx,λy,λz分别为x,y,z方向上的导热系数;qV为热源密度,是电机各部件单位体积产生的损耗;α为对流散热系数;Tf为周围流体的温度。

由变分原理可知,式（1）的等价变分方程为

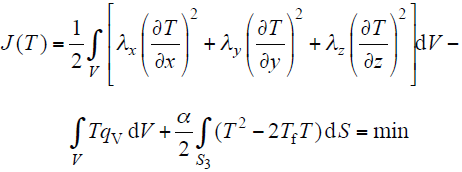
对其作离散化处理后,可得到三维温度场有限元方程

KT=F

式中,T为求解域内全部节点温度所形成的温度阵列;K和F分别为总体系数矩阵和总体右端矢量。

对方程进行求解后可得到求解域内全部节点的温度值。

3.2 电机热源的分析

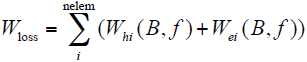
定子铁心的热源主要来自于绕组铜耗和铁心损耗[10,13,15-16]。通过电磁计算可以求得电机铁心中的磁场分布,其铁耗的计算公式为

式中,Whi(B)为单元磁滞损耗;Wei(B)单元焦耳损耗。

由式（5）可以看出,在分析铁耗时,将铁耗分为磁滞损耗和焦耳损耗两部分[17]。铁心各部分磁通密度的准确度对于铁耗计算的准确性有重要影响。由于永磁体上的涡流损耗相较于电机的其他损耗较小,因而在计算中忽略,同时忽略不计转子铁心中产生的铁心损耗。

3.3 电机各部分导热系数及边界条件

电机中的热量传递方式主要有热传导和对流换热,即导热和对流的综合过程[11,19]。由传热的基础知识可知,上述过程与介质的导热系数和表面传热系数直接有关。由傅里叶定律可知,导热系数是当温度梯度为1时,单位时间内通过单位面积的导热量。导热系数的大小与材料的性质有关,同一材料的导热系数随温度、压力、多孔性和均匀性等因素而变化,其中温度是决定性因素。对于绝大多数物质而言,材料温度尚未达到融化或气化以前,导热系数可以近似地认为是线性规律变化,即：λ0 = λ0(1 + bt)。其中,λ0指温度为零时的导热系数;b是由试验确定的常数。本文中永磁电机主要材料的导热系数见表1。

表1   电机主要材料导热系数

Tab.1  Thermal conductivity of main materials

部件名称导热系数/(W/m·K)
定子铁心39
空气0.0305
定子绕组385
永磁体9
转子极靴4.43
转子轭部45

新窗口打开| 下载CSV


计算定转子全域温度场时,需要对气隙进行特殊处理,可以用热方式换热的效果等价气隙中对流方式换热的效果。有效导热系数可按下述方法求取。

假定定子内表面和转子外表面为光滑圆柱面,而气隙中的雷诺数Re可表示为

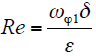
式中,ωϕ1为转子的圆周速度;δ为气隙的长度;ε为空气的运动粘度。

临界雷诺数Recr的表达式为

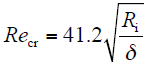
式中,Ri为定子内径。

当Re<Recr时,气隙中的空气流动为层流,有效导热系数λeff等于空气导热系数;当Re>Recr时,气隙中的空气流动为紊流。计算得出

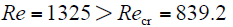
此时,气隙中的空气流动为紊流,气隙的有效导热系数为

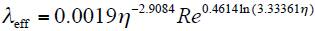
式中,η = ro/Ri;ro为转子外径;Ri为定子内径。

通过计算得出气隙有效导热系数为0.103(W/m·K)。此外,电机温度场计算的边界条件包括：生热边界、散热边界和绝缘边界。

4 模型建立及网格剖分

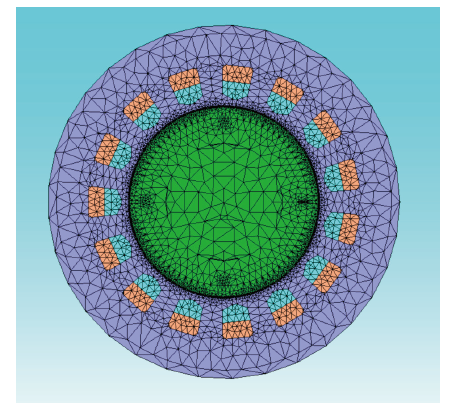
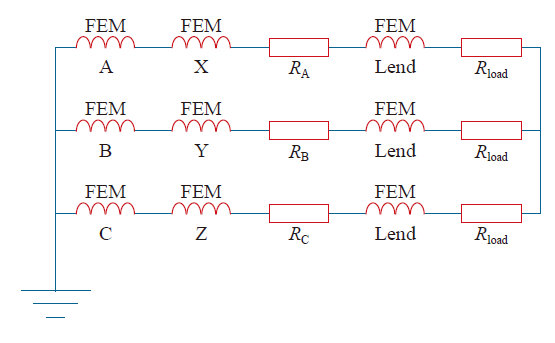
电磁场分析的基本流程,可分为前处理、解算和后处理三个阶段。前处理阶段主要包括建立分析模型（电机磁场有限元模型和功率变换器电路模型）、设定材料属性、边界条件和仿真参数以及网格剖分等几个步骤。在后处理阶段,可以将电机磁场有限元模型中每一个单元或节点的磁场数据以及电路模型中的电流、电压等数据提取出来进行数据分析和处理。

本文中所研究的分数槽永磁电机模型和网格剖分分别如图1和图2所示。图3为电机的外电路模型。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   电机模型

Fig.1   Model of machine


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   网格剖分

Fig.2   Mesh of machine


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   外电路模型

Fig.3   Circuit model


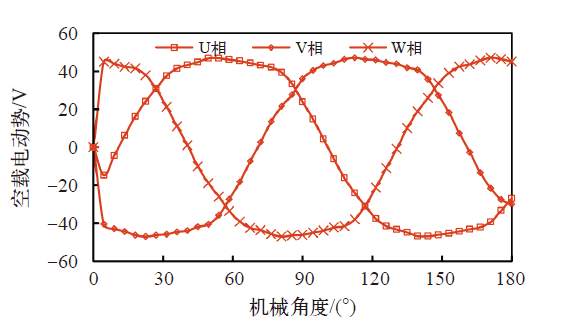
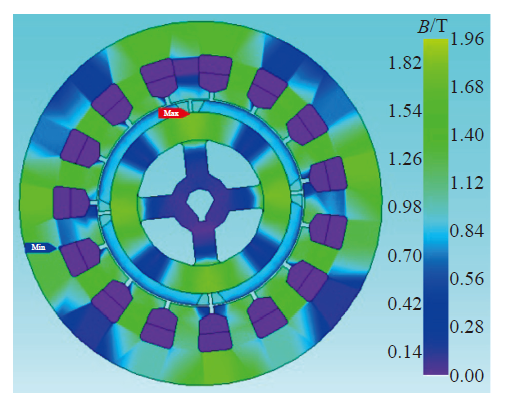
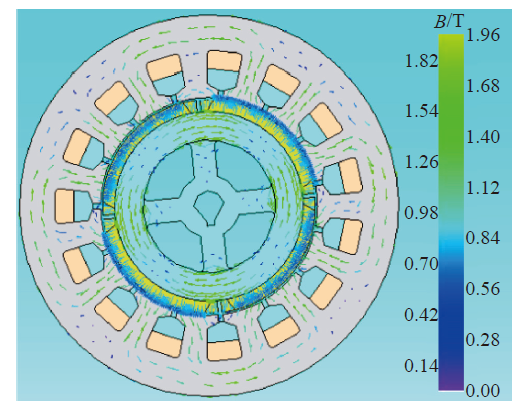
5 电机磁场仿真结果

电机空载电动势及齿槽转矩波形分别如图4和图5所示。由于采用开口槽设计,其空载电动势具有一定程度的齿谐波。齿槽转矩是永磁体不通电时永磁体和铁心之间相互作用产生的转矩,是由永磁体与电枢齿相互作用力的切向分量的波动引起的。齿槽转矩导致转矩波动,影响系统的控制精度,同时产生振动和噪声[2]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   空载电动势

Fig.4   No-load electromotive force


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   齿槽转矩

Fig.5   Cogging torque


图6为电机磁密的整体分布情况,可以看出转子上有部分饱和现象,其中定子铁心的平均磁密为0.87T,转子铁心平均磁密为0.95T。图7为电机定转子磁矢量图,通过图7可以分析电机漏磁分布情况。通过以上对电机磁场的计算分析可以得出,电机的铜耗和铁耗分别为34W和5.77W。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   磁通密度云图

Fig.6   Magnetic flux density


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   磁通密度矢量图

Fig.7   Flux density vector


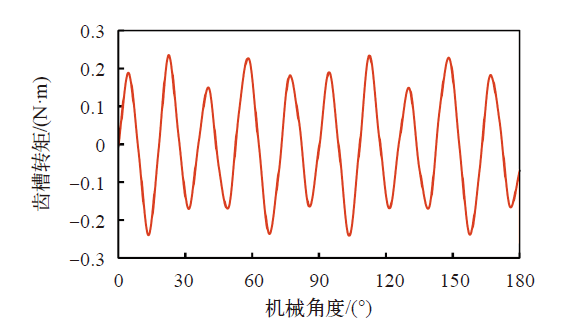
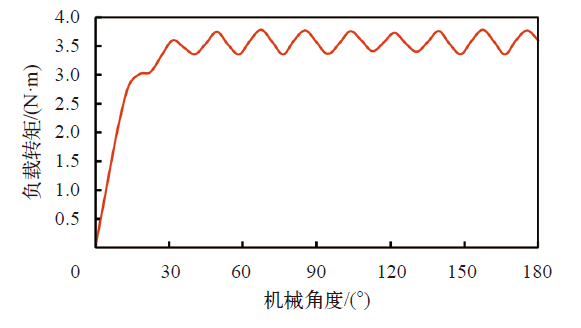
图8为电机额定负载时的输出转矩。此时,电机的输出转矩为3.5N·m,但是存在转矩脉动,该脉动是由于齿槽转矩和控制方式产生的,约为7%。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   负载转矩

Fig.8   Load torque


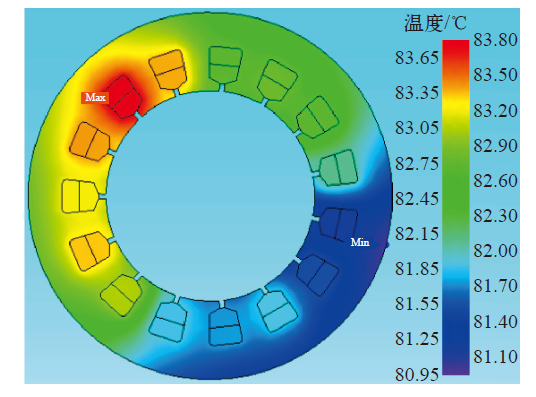
6 永磁电机温度场计算结果分析

通过磁场分析得到的电机损耗作为热源对其温度场进行仿真计算,结果如图9和图10所示。从仿真结果中可以看出,电机的最高温度出现在定子齿部,大约为83.8℃。这是因为绕组绝缘及绝缘介质的导热系数很小,而且线圈绕组也是一个大功率的发热源[20]。具体各部分温升情况在表2中给出。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   定子铁心及绕组温度分布

Fig.9   The temperature distribution of stator core and winding


图10

新窗口打开| 下载原图ZIP| 生成PPT

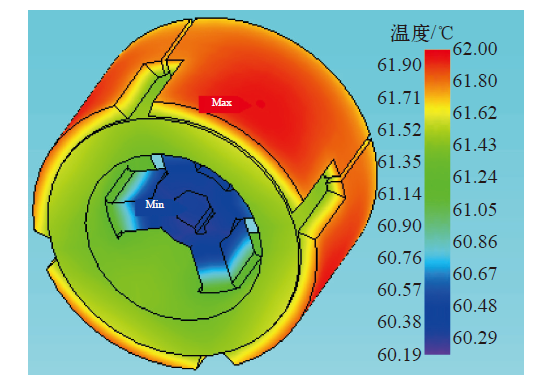
图10   转子及永磁体温度分布

Fig.10   The temperature distribution of rotor and permanent magnet


表2   电机温度场计算值

Tab.2  Thermal field calculation results

区域温升/℃
最高温升62.47
定子绕组最高温升62.47
定子齿部平均温升62.34
定子轭部平均温升61.85
永磁体最高温升41.66
永磁体平均温升41.25
转子轭部平均温升40.60

新窗口打开| 下载CSV


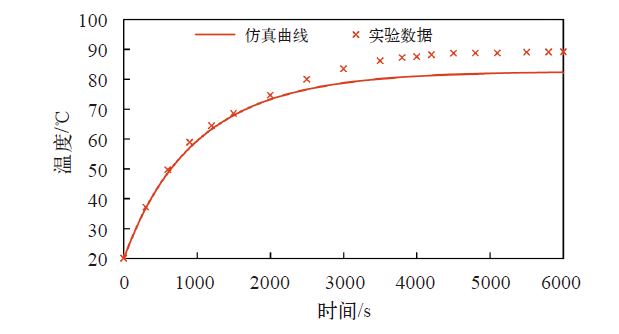
电机运行时发热均来自其损耗。其中定子和绕组既是发热部件也是传热部件,别的部件为传热部件。随着电机温度的升高,它与周围介质之间的温差逐渐增大,散失到周围空间中的热量相应地也逐渐增多,本身温度升高的速度则逐渐变慢,最后电机产生的全部热量都传给周围介质,达到热稳定状态。通常每小时温度变化小于1℃时,即认为已经达到热稳定状态。从图11的电机定子温度变化仿真曲线可以看出,电机运行一段时间后,温度最大值达到了84℃。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   电机定子温度变化仿真曲线和实验数据

Fig.11   Simulation curve of motor temperature and experimental data


图12给出了电机样机模型,通过对样机进行实验得出的定子铁心温度测量数据可知,当电机运行70min后,定子铁心中的平均温度达到了88℃,之后温度基本保持恒定,与计算结果基本一致。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   样机模型

Fig.12   Prototype motor


7 结论

本文通过三维有限元法对分数槽永磁电机的磁场进行了分析与计算,并基于磁场计算推导得出电机损耗分布,利用各部分损耗作为热源对电机的磁热耦合展开分析。在此基础上,对样机进行实验测量,从实验结果看出,电机模型各部分的温度分布趋势与计算数据基本一致,为后续电机的结构优化设计奠定了理论基础。

参考文献

唐任远, 等. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2000.

[本文引用: 1]

王秀和, 等. 永磁电机[M]. 北京: 中国电力出版社, 2011.

[本文引用: 2]

梅凡, 谢宝昌, 高强, 等.

永磁电机分析的场路耦合时步有限元法

[J]. 电机与控制应用, 2012,39(9):5-9.

[本文引用: 1]

Mei Fan, Xie Baochang, Gao Qiang, et al.

Circuit-field coupled time-stepping finite-element method in analysis of permanent magnet motor

[J]. Electric Machines and Control Application, 2012,39(9):5-9.

[本文引用: 1]

刘瑞芳, 严登俊, 胡敏强.

永磁无刷直流电动机场路耦合运动时步有限元分析

[J]. 中国电机工程学报, 2007,27(12):59-64.

[本文引用: 1]

Liu Ruifang, Yan Dengjun, Hu Minqiang.

Field circuit and movement coupled time stepping finite element analysis on permanent magnet brushless DC motors

[J]. Proceedings of the CSEE, 2007,27(12):59-64.

[本文引用: 1]

刘瑞芳.

基于电磁场数值计算的永磁电机性能分析方法研究

[D]. 南京:东南大学, 2002.

[本文引用: 1]

董剑宁, 黄允凯, 金龙, 等.

高速永磁电机设计与分析技术综述

[J]. 中国电机工程学报, 2014,34(27):4640-4653.

[本文引用: 1]

Dong Jianning, Huang Yunkai, Jin Long, et al.

Review on high speed permanent magnet machines including design and analysis technology

[J]. Proceedings of the CSEE, 2014,34(27):4640-4653.

[本文引用: 1]

孔晓光.

高速永磁电机定子损耗和温升研究

[D]. 沈阳:沈阳工业大学, 2011.

[本文引用: 1]

李伟力, 李勇, 杨雪峰, 等.

大型空冷汽轮发电机定子端部温度场与流体场的计算与分析

[J]. 中国电机工程学报, 2009,29(36):80-87.

[本文引用: 1]

Li Weili, Li Yong, Yang Xuefeng, et al.

Temperature and fluid flow field calculation and analysis of stator end of air cooled turbo-generator

[J]. Proceeding of the CSEE, 2009,29(36):80-87.

[本文引用: 1]

孔晓光, 王凤祥, 邢军强.

高速永磁电机的损耗计算与温度场分析

[J]. 电工技术学报, 2012,27(9):166-173.

[本文引用: 2]

Kong Xiaoguang, Wang Fengxiang, Xing Junqiang.

Losses calculation and temperature field analysis of high speed permanent magnet machines

[J]. Transaction of China Electrotechnical Society, 2012,27(9):166-173.

[本文引用: 2]

胡田, 唐任远, 李远, 等.

永磁风力发电机三维温度场计算及分析

[J]. 电工技术学报, 2013,28(3):122-126.

[本文引用: 3]

Hu Tian, Tang Renyuan, Li Yuan, et al.

Thermal analysis and calculation of permanent magnet wind generators

[J]. Transactions of China Electrotechnical Society, 2013,28(3):122-126.

[本文引用: 3]

Popescu M, Dorrell D G.

Proximity losses in the windings of high speed brushless permanent magnet ac motors with single tooth windings and parallel paths

[J]. IEEE Transactions on Magnetics, 2013,49(7):3913-3916.

[本文引用: 2]

Aglen O, Andersson A.

Thermal analysis of a high speed generator

[C]. IEEE Industry Applications Conference, 2003: 547-554.

[本文引用: 1]

Kolondzovski Z.

Thermal and mechanical analyses of high speed permanent magnet electrical machines

[D]. Finland: Aalto University, 2010.

[本文引用: 2]

程志光, 高桥则雄, 博扎德·弗甘尼, 等. 电气工程电磁热场模拟与应用[M]. 北京: 科学出版社, 2009.

[本文引用: 1]

孔晓光, 王凤翔, 徐云龙, 等.

高速永磁电机铁耗的分析与计算

[J]. 电机与控制学报, 2010,14(9):26-30.

[本文引用: 2]

Kong Xiaoguang, Wang Fengxiang, Xu Yunlong, et al.

Analysis and calculation of iron losses of high-speed permanent magnet machines

[J]. Electric Machines and Control, 2010,14(9):26-30.

[本文引用: 2]

Xyptras J, Hatziathanassiou V.

Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect

[J]. IEEE Transactions on Energy Conversion, 1999,14(4):996-1003.

[本文引用: 1]

Munteau G, Blinder A, Schneider T.

Loss measurement of a 40 kW high-speed bearingless PM synchronous motor

[C]. 2011 IEEE Energy Conversion Congress and Exposition. Phoenix, 2011: 722-729.

[本文引用: 1]

林平, 关德林, 王静怡.

13 kW 磁力耦合器试验台直流电动机供电单元的设计

[J]. 电气应用, 2016,35(19):84-87.

魏大勇, 孟大伟, 温嘉斌. 电机内热交换[M]. 北京: 机械工业出版社, 1998.

[本文引用: 1]

高彦骋, 刘卫国.

基于Ansys的11kW无刷直流电动机温度场分析

[J]. 微电机, 2008,41(9):13-15.

[本文引用: 1]

Gao Yancheng, Liu Weiguo.

Analysis of temperature field for BLDCM based on Ansys

[J]. Micromotors, 2008,41(9):13-15.

[本文引用: 1]

/

〈 〉