基于模糊控制与自适应步长相结合的光伏发电系统最大功率点跟踪研究

doi:10.11985/2017.03.005

基于模糊控制与自适应步长相结合的光伏发电系统最大功率点跟踪研究

万庆祝, 张翃帆

北方工业大学电气与控制工程学院北京 100144

Research on Maximum Power Point Tracking of Photovoltaic Generation System Based on Fuzzy Control and Adaptive Step Combination

Wan Qingzhu, Zhang Hongfan

North China University of Technology Beijing 100144 China

收稿日期: 2016-05-16 网络出版日期: 2017-03-25

基金资助:

北京市教委专项基金资助项目. XN097
北京市电力节能协同创新2011研究项目. PXM2016_014212_000016

Received: 2016-05-16 Online: 2017-03-25

作者简介 About authors

万庆祝,男 1975年生,博士,副教授,研究方向为分布式发电。

张翃帆,女 1993年生,硕士研究生,研究方向为分布式发电。

摘要

光伏发电已逐渐得到人们的重视和使用,根据光伏电池输出特性非线性的特点,采用了模糊控制的方法来进行最大功率点的跟踪。本文搭建了光伏发电系统的仿真模型,设计了模糊控制器,并为了弥补传统步长算法在光伏发电系统最大功率点跟踪上的缺陷,采用了自适应步长调整法来自动调整被控量。通过与传统定步长、变步长的仿真结果进行比较,得出了基于模糊控制的自适应步长调整法,可以快速实现光伏发电系统的最大功率点的跟踪控制,并使输出一直维持在稳定值。

关键词： 光伏发电 ; 最大功率点跟踪 ; 模糊控制 ; 自适应步长调整法

Abstract

Solar power generation has been gradually getting people's attention and using, according to the characteristics of the output characteristic of PV cells, the fuzzy control method is used to track the maximum power point, which makes up the deficiency of the traditional control method. The simulation model of the photovoltaic power generation system is built, the fuzzy controller is designed, and in order to make up for the defects of the traditional step size algorithm in the maximum power point tracking of photovoltaic generation system, the adaptive step size adjustment method is adopted to adjust the controlled volume automatically. By comparing the simulation results with the traditional fixed step size and variable step size, the adaptive step size adjustment method based on fuzzy control can realize the maximum power point tracking control of photovoltaic power generation system, and the output value has been maintained at a stable value.

Keywords： Photovoltaic power generation ; maximum power point tracking ; fuzzy control ; adaptive step size adjustment method

PDF (2330KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

万庆祝, 张翃帆. 基于模糊控制与自适应步长相结合的光伏发电系统最大功率点跟踪研究. 电气工程学报[J], 2017, 12(3): 33-40 doi:10.11985/2017.03.005

Wan Qingzhu. Research on Maximum Power Point Tracking of Photovoltaic Generation System Based on Fuzzy Control and Adaptive Step Combination. Journal of Electrical Engineering[J], 2017, 12(3): 33-40 doi:10.11985/2017.03.005

1 引言

太阳能是一种新型的绿色可再生能源,太阳能发电已普遍被人们认为是最清洁的发电方式,光伏发电系统面临的最大问题就是太阳能光伏阵列的光电转换效率太低,只有12%~17%^[1],因此,光伏发电系统的最大功率点跟踪（Maximum Power Point Tracking,MPPT）问题已成为各国研究的焦点。

目前国内外研究主要集中于通过改进光伏发电系统的最大功率点控制算法,来实现光伏发电系统的最大功率输出。知名学者葛丽芳等提出了一种固定电压法来实现光伏发电系统MPPT,其主要原理是基于光伏电池的开路电压与最大功率点之间的耦合关系,来调节系统的工作点电压,达到最大功率输出。其优点是输出电压为固定值,易于控制;但当外界环境发生变化时,却无法实时跟踪光伏电池的输出状态,给光伏发电系统的输出功率造成大量的损失^[2,3]。任玲等提出了一种扰动观察法,该方法操作简单,测量参数少,易于实现,是目前计算光伏发电系统MPPT最常用的方法^[4]。其原理是给系统引入一个小的变化进行观测和比较,以此来判断和调节输出电压的变化方向,使光伏电池达到最大功率点,但是此方法的控制精度相对较低,反应速度比较慢,只适合外界环境变化不大的情况^[5,6]。黄瑶等提出了一种电导增量法来求解光伏发电系统MPPT,该方法是通过光伏阵列输出的动态电导值和静态电导值的负数之间的关系来调整工作电压,实现最大功率点的跟踪。该控制方法能很快地检测到外界环境突然的变化,并进行追踪与调节,保证系统继续稳定运行,但是它的算法结构相对复杂,不易实现^[7,8]。本文采用模糊控制^[9]的方法进行光伏发电系统最大功率点的跟踪,可以弥补上述传统控制方法的缺点,达到比较理想的控制效果。

本文先对光伏电池和光伏发电系统的控制电路进行建模;然后介绍并比较了几种常用的步长算法。选用智能控制中模糊控制的理论,并采取模糊控制与自适应占空比步长相结合的算法,来实现光伏发电系统最大功率点的跟踪控制,设计了模糊控制器,与光伏电池的模型相结合,进行光伏发电系统的建模与仿真。最后对比分析了定步长调整法、变步长调整法以及自适应步长调整法的仿真结果,结果表明自适应步长调整法明显优于其他两种算法的控制效果。

2 光伏发电系统MPPT实验原理及控制电路

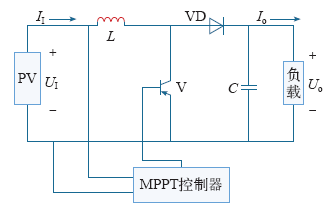
2.1 光伏发电系统原理组成

光伏发电系统主要由光伏电池组件、控制电路、MPPT控制器和负载等组成。光伏电池的作用是将太阳能照射的光能转换为电能;控制电路采用DC-DC变换电路,由升压斩波变换电路构成^[10];MPPT控制器通过模糊控制与自适应步长相结合的算法实现其功能。光伏发电系统的等效电路图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 光伏发电系统原理图

Fig.1 Principle diagram of photovoltaic power generation system

2.2 光伏电池的建模与仿真

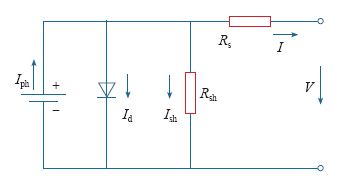
光伏电池模型可等效为一个电压源和一个二极管并联,再串联和并联上其内部的等效电阻,等效电路如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 光伏电池等效模型

Fig.2 Equivalent model of photovoltaic cells

由图2可得出光伏电池的输出电流I与输出电压V的关系为

(1)

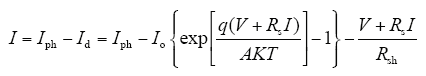
式中,I_ph为光伏电池经由光照射后所产生的电流;I_d为二极管电流;R_sh和R_s分别为材料内部等效的并联和串联电阻;T为电池板表面温度（K）;A为电池板理想因数（A = 1~2）;q为电子所含的电荷量（1.6×10^-19C）;K为波尔兹曼常数（1.38× 10^-23J/K）。

I_o表示光伏电池板的逆向饱和电流,可表示为

(2)

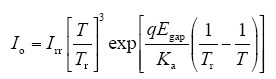
式中,T_r为光伏电池板的参考温度;I_rr为光伏电池在温度临界时的逆向饱和电流;E_gap为半导体材料跨越能带间隙时所需的能量。

当光照较强时,光电流远远大于(V + IR_s)/R_sh,故光伏电池的输出特性方程可简化为式（3）。

(3)

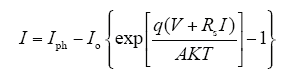
根据光伏电池输出特性的数学模型,本文选择Solarex MSx60 60W光伏电池阵列^[11]进行建模,在Matlab软件中搭建仿真模型。

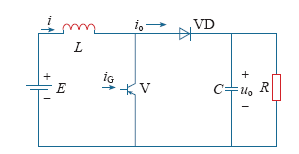
2.3 MPPT控制电路

光伏发电系统的MPPT控制电路引入了DC-DC变换器^[12],采用Boost升压电路来实现光伏发电系统中最大功率点跟踪的功能,Boost电路原理图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 升压斩波电路原理图

Fig.3 Boost chopper circuit schematic

Boost电路由开关V、二极管VD、储能电感L和滤波电容C以及负载R组成。在理想状态下,电路中电感L和电容C均很大。Boost电路的输入输出关系为

(4)

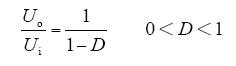
由图3可知输入电阻为

(5)

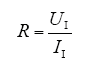
式中,U_I为Boost电路输入电压;I_I为输入电流;U_o为输出电压;I_o为负载电流。

R_L为负载电阻,根据功率平衡,可得

(6)

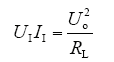
由式（4）~式（6）可得Boost电路的等效输入电阻为

(7)

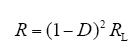
由此可见,通过调节占空比D,即可改变Boost电路的输入电阻R,如果使其刚好等于光伏电池的等效内阻,则光伏电池输出最大功率^[13]。根据以上公式在Matlab中搭建Boost电路的仿真模型。

3 模糊控制与自适应步长相结合的最大功率点跟踪算法

3.1 传统步长算法

在扰动观察法中,可通过改变DC-DC变换器中Boost电路的占空比D对系统进行观测和比较,实现最大功率点的跟踪控制。传统的步长算法有定步长调整法和变步长调整法。定步长调整法是指将步长调整值设为一固定参数,对下一时刻的占空比施加扰动,改变固定的步长值,使光伏电池运行在最大功率点^[14]。这种算法对于扰动步长值的选取比较麻烦,控制精度也不够准确。变步长调整法是根据功率的变化率的几个不同阶段,赋予不同的步长调整值。根据当前时刻与前一时刻的功率变化,决定输出电压的调整方向,并根据功率的变化大小来调整步长的变化,这样可以更快速地跟踪到系统的最大功率点^[15]。

3.2 自适应占空比步长调整法

在传统的变步长调整法中,调整占空比D时会产生如何判断步长调整值大小的问题,若调整值过大,会造成系统稳态误差增大;若调整值过小,跟踪时间就会变长,从而影响系统的动态响应特性。基于此,本文采用一种优化的变步长调整方法,加入一个步长调整值参数a,使系统能自动调整步长选择的大小,改善系统的稳态误差与动态响应问题^[16]。自动调整器如下

(8)

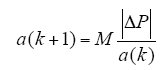
式中,a(k)为占空比D的步长调整值,在0和1之间变化;ΔP是功率的变化量;M为一常数。

当外界环境因素突然变化较大时,一般的扰动观察法会认为是输出电压或电流的增减导致了输出功率的变化,在此情况下调整步长,可能会导致控制器远离最大功率点。式（8）可解决这一问题。当ΔP/a(k)较小时,说明此时只有占空比D的变化来决定输出功率P的大小,因此下一时刻占空比的步长调整值a(k + 1)的变化不应过大;当ΔP/a(k)较大时,表示功率P的变化主要是由温度、光照强度等外界因素造成的,此时应增大a(k + 1)来保证系统快速跟踪到最大功率点。当功率P的波动变小后,调整器会认为系统已达到了最大功率点,将自动减小a(k + 1)的变化来维持系统的稳定输出。由此可见该方法具有很强的自适应性,因此称为自适应占空比步长调整法^[17]。

3.3 与自适应步长相结合的模糊控制器的设计

最大功率点跟踪控制一般是通过检测当前时刻的输出电压、电流值,得出此时的输出功率并与前一时刻比较,以此判断电压的调整方向^[18]。这就需要设计两个控制循环结构来测量两个量。为了减小控制器的设计复杂程度,决定采用改变占空比D的方法来调整系统的输入输出关系,并且为了解决在调节占空比D时存在的调整步长大小的选择问题,本文采取了自适应步长调整法,加入了步长调整值a,使系统通过当前时刻与前一时刻的输出功率的比较,自动调整步长的变化大小。

3.3.1 输入、输出量的选择

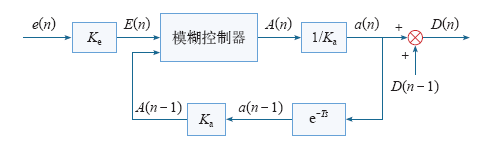
模糊控制器的输入量是第n时刻的功率变化量E(n),和第n-l时刻的占空比步长调整值A(n-l),输出量是第n时刻的占空比步长调整值A(n)。控制原理如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 光伏系统模糊控制器原理图

Fig.4 Fuzzy controller principle of photovoltaic system

其中,K_e、K_a分别为量化因子,是将功率差实际值e和步长实际值a转换到模糊控制器的论域范围内,使其分别变为模糊值;e^-^Ts是一个延迟环节。

3.3.2 输入、输出模糊集的确定

对于输入、输出量的偏差大小,通过定义模糊集来表示。

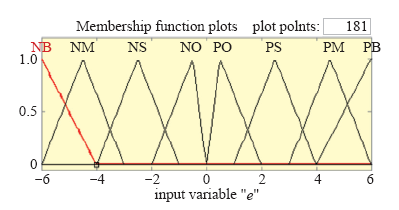
将功率变化量E(n)定义为8个模糊集：E(n) = {NB,NM,NS,NO,PO,PS,PM,PB},取值范围为[-6,+6]。

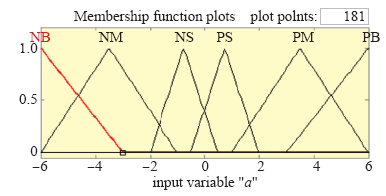
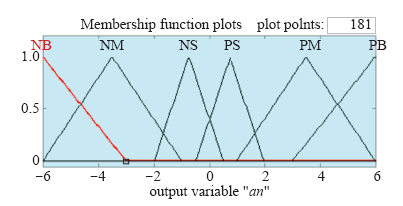
将占空比步长调整值A(n)和A(n-l)定义为6个模糊集：A(n) = {NB,NM,NS,PS,PM,PB},A(n - 1) = {NB,NM,NS,PS,PM,PB},取值范围为[-6,+6]。

NB,NM,NS,NO,PO,PS,PM,PB分别表示负大,负中,负小,负零,正零,正小,正中,正大的模糊概念。

3.3.3 确定与自适应步长相结合的模糊控制规则

光伏电池的输出功率P与占空比D之间的特性关系,跟其与输出电压U之间的关系类似,也呈非线性关系^[19],因此制定如下规则：

（1）若当前时刻的输出功率是增大的,则控制器维持前一时刻的步长调整方向;若当前时刻功率减小,则步长调整值取相反方向。

（2）在离最大功率点较远的地方,选择较大的步长调整值调整;在接近最大功率点处,则采用小步长来进行调整。

另外,考虑到外界条件对系统的影响,还添加了如下规则：

若因外界环境因素变化而引起光伏电池的输出功率发生较大变化时,系统要通过自适应步长调整来自动进行调节。

模糊控制语言规则的一般形式为：如果“前提”,那么“结论”（If…Then…）。

对于光伏系统MPPT的控制,例如当功率变化量E(n)是负大（NB）,前一时刻的占空比步长调整值a(n-1)也是负大（NB）时,说明输出功率在减小,而且离最大功率点较远,则此时占空比的步长调整值应与前一时刻的方向相反,并采取较大步长调整来加快跟踪速度。因此,输出量当前时刻的步长调整值a(n)应是正大（PB）。

用语言规则形式来表示上述规则为：如果功率变化量为负大且前一时刻步长调整值为负大,那么当前时刻步长调整值为正大。

通过定义的输入、输出模糊集数量,共形成了48条规则。

3.3.4 建立模糊控制规则表

根据上文所确定的与自适应步长相结合的模糊控制规则,建立的模糊控制规则表,见表1。

表1 MPPT模糊控制规则表

Tab.1 Fuzzy control rules table of MPPT

A				E
A	NB	NM	NS	NO	PO	PS	PM	PB
NB	PB	PM	PS	PS	NS	NS	NS	NS
NM	PB	PB	PM	PS	NS	NS	NS	NS
BS	PB	PB	PM	PS	NS	NS	NS	NS
PS	NS	NS	NS	NS	PS	PM	PB	PB
PM	NS	NS	NS	NS	PS	PM	PB	PB
PB	NS	NS	NS	NS	PS	PS	PM	PB

新窗口打开| 下载CSV

3.3.5 确定隶属函数

通过Matlab中的Fuzzy工具箱来建立MPPT控制器的隶属函数,选择三角形作为隶属函数的形状^[20]。光伏电池的输出功率在最大点的两侧是不对称的,因此三角形的形状也设置为不对称的。输入量和输出量的隶属函数如图5~图7所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 功率变化量e的隶属函数

Fig.5 Membership function of power variation e

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 n-1时刻步长调整值a(n-1)的隶属函数

Fig.6 Membership function of (n-1) time step adjustment value a(n-1)

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 n时刻步长调整值a(n)的隶属函数

Fig.7 Membership function of (n) time step adjustment value a(n)

4 光伏发电系统的仿真

4.1 光伏系统仿真模型

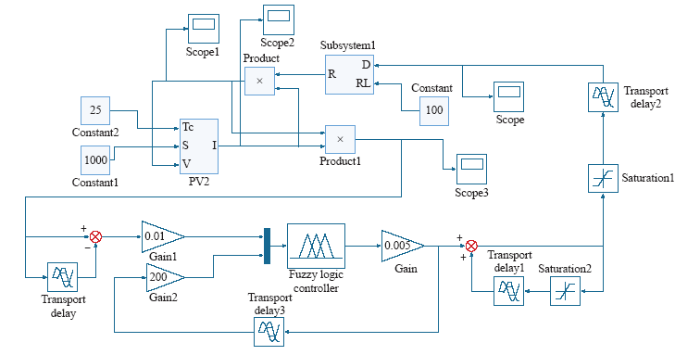
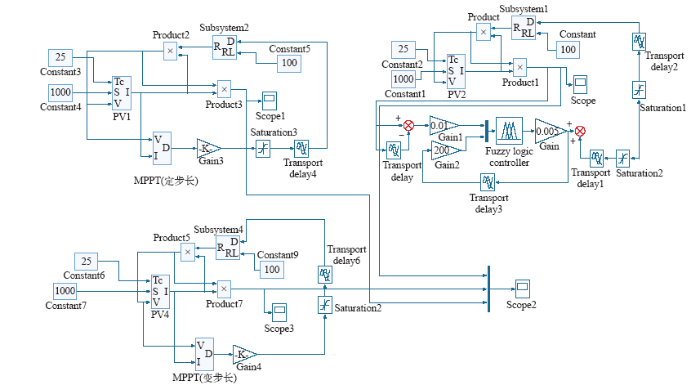
光伏发电系统由PV模块、MPPT模块和控制电路模块三部分组成。仿真电路图如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 光伏系统仿真电路图

Fig.8 Photovoltaic system simulation circuit

图8中,Transport delay为延迟环节,实现系统一个采样周期的延迟。PV模块是由多个光伏电池组成的光伏阵列,本文选择Solarex MSx60 60W光伏电池阵列,在标准测试条件下,即光照强度1 000W/m²,温度为25℃,其基本参数见表2。PV模块与控制电路模块的模型均根据前文的公式搭建。负载为100Ω,量化因子K_e为0.01,K_a为200,用模糊控制器来实现MPPT的控制。

表2 Solarex MSx60 60W标准测试条件下参数

Tab.2 Solarex MSx60 60W parameters under standard test conditions

参数	典型值
最大功率P_m/W	59.9
峰值工作电流I_m/A	3.5
峰值工作电压U_m/V	17.1
短路电流I_sc/A	3.74
开路电压U_oc/V	21.0
短路电流温度系数K_t/(mA/℃)	2.06
开路电压温度系数K_T/(V/℃)	-0.07

新窗口打开| 下载CSV

本文采取的是模糊控制与自适应步长相结合的MPPT算法,为了证明自适应步长调整法比其他方法能更加快速有效地实现光伏发电系统最大功率点跟踪的控制,本文还搭建了定步长调整法以及传统的变步长调整法的仿真模型,在同样的外界环境下（光照强度1 000W/m²,环境温度25℃）,与模糊控制法下的自适应步长调整法进行仿真结果的对比,仿真电路图如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 三种步长算法仿真电路图

Fig.9 Three step size algorithm simulation circuit

4.2 仿真结果分析

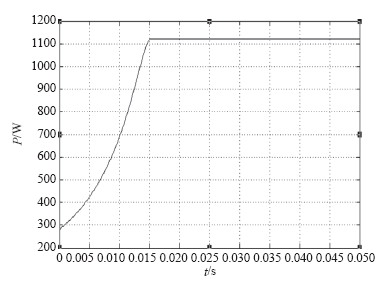
模糊控制与自适应步长相结合算法的输出功率的仿真结果如图10所示。由仿真结果可知,当时间为0.015s时,系统输出最大功率,此时功率值为1 120W左右。这说明经过模糊控制器的控制可使光伏发电系统迅速平稳地跟踪到最大功率点,并且在最大功率点几乎没有波动。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 输出功率P变化曲线

Fig.10 Output power P curve

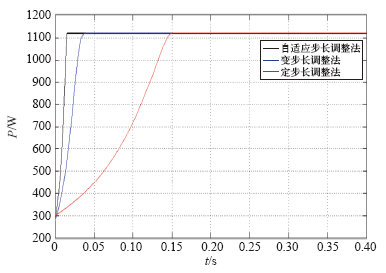
三种步长算法的仿真结果对比如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 仿真结果对比图

Fig.11 Comparison of simulation results

通过图11可知,定步长算法实现的MPPT要经过0.15s才能完成,传统变步长算法要经过0.035s以后可以实现,已经快于定步长算法,而自适应步长调整法仅用了0.015s就实现了系统的最大功率点跟踪控制,明显优于前两种算法,并保证了系统良好的稳定性。

5 结论

光伏发电系统是一个高度非线性系统,也很难用精确的数学模型来描述,因此采用模糊控制的方法进行光伏电池的最大功率点跟踪能有效弥补传统控制方法的不足。

本次设计用MPPT模糊控制器通过控制升压电路的占空比来调节光伏发电系统的输出功率,并采用了自适应步长调整法,使系统可以自动调整步长的变化量,为了证明这种步长算法的优化性,搭建了三种步长调整方法的仿真模型,将定步长调整法、传统变步长调整法以及自适应步长调整法的控制结果进行比较,在同样的外界环境条件下观察系统的输出波形。仿真结果表明,自适应步长调整法能明显优于其他两种算法的控制效果。因此,基于模糊控制的自适应步长调整法的最大功率点跟踪控制能使光伏发电系统快速达到最大功率点,并维持稳定的输出,保证系统一直工作在最佳状态。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

胡海峰

基于模糊PID控制的太阳能光伏发电系统的MPPT研究

[D]. 长沙:湖南大学, 2011.

A				E
A	NB	NM	NS	NO	PO	PS	PM	PB
NB	PB	PM	PS	PS	NS	NS	NS	NS
NM	PB	PB	PM	PS	NS	NS	NS	NS
BS	PB	PB	PM	PS	NS	NS	NS	NS
PS	NS	NS	NS	NS	PS	PM	PB	PB
PM	NS	NS	NS	NS	PS	PM	PB	PB
PB	NS	NS	NS	NS	PS	PS	PM	PB

A				E
A	NB	NM	NS	NO	PO	PS	PM	PB
NB	PB	PM	PS	PS	NS	NS	NS	NS
NM	PB	PB	PM	PS	NS	NS	NS	NS
BS	PB	PB	PM	PS	NS	NS	NS	NS
PS	NS	NS	NS	NS	PS	PM	PB	PB
PM	NS	NS	NS	NS	PS	PM	PB	PB
PB	NS	NS	NS	NS	PS	PS	PM	PB