1 引言
随着分布式电源系统的广泛应用,恒功率负载(Constant Power Load,CPL)在电源系统负载中的比例越来越大,如在未来多电飞机直流配电系统中,75%的负载是CPL[1]。传统直–直变换器优化设计时只考虑恒阻性负载,当带CPL时变换器动态性能和稳定性得不到保证。
CPL的负阻特性会对变换器输出电压稳定产生影响[1,2],因此抑制负阻影响对提高变换器输出电压稳定范围有着重要的意义。增大母线电容可以提高级联系统的电压稳定性[3],但会导致系统动态响应变慢。文献[4,5]利用平均模型和相平面法分析了带CPL的DC-DC变换器的稳定性,如果电路参数全部给定,该方法可以用于验证系统的稳定性,但是计算烦琐,对数学软件依赖性强,一旦负载参数发生变化,需重新计算验证系统的稳定性,在小信号情况下,直流分布式电源系统稳定性可以通过测量阻抗比的奈氏曲线来判断[6],而文献[7]提出一种新颖的基于无源稳定性的判据(Passivity Based Stability Criterion,PBSC)判断系统的稳态性能,PBSC利用阻抗的无源性而不是利用阻抗比判据,可以减少如Middlebrook判据及其扩展判据的人为设计保守性和灵敏性。
本文首先分析CPL的负阻特性,对带CPL的Buck-Boost变换器的稳定性进行了分析,并研究了抑制CPL负阻特性的无源控制策略,仿真结果表明本文所提无源控制策略的可行性。
2 CPL模型
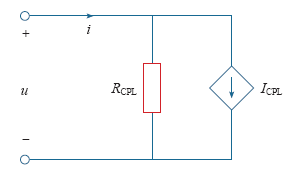
对于图1所示的Buck-Boost变换器,如果变换器的负载为恒阻负载,可获得稳定的输出电压,那么无论输入电压大小,变换器输出功率为一个定值,即P = Uc2/R。如果假定改变变换器的输入电压,且变换器的效率没有明显变化,输入功率就是恒定的,那么在变换器的输入端就相当于CPL。
图1
使用线性控制方法来研究CPL的问题,它需要在稳定运行点处建立CPL线性方程模型。对于CPL,可以写为
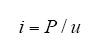
式中,i为流过CPL的电流;u为CPL两端的电压;P为CPL的功率。
在给定的稳定工作点(U,I)附近有
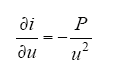
其特性曲线可近似于一条与该曲线相切的直线,设直线公式为i = au + b,则由式(2),有a = -P/U2,将点(U,I)带入直线中可求b = 2P/U,于是该切线公式为
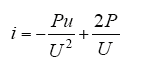
于是CPL可近似等效于一负阻RCPL = -U2/P与一受控电流源ICPL = 2P/U的并联电路,如图2所示。
图2
3 带CPL的Buck-Boost变换器稳定性
对于单端口网路,当且仅当网路从外界吸收功率,则该网络是无源的,网络就是稳定的。即在所有时间段T内
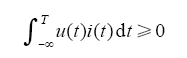
式中,u(t)、i(t)分别为单端口网络两端电压和流过网络的电流。
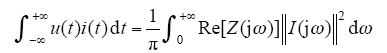
式中,I*(jω) = I(-jω),I*(jω)为I(jω)的共轭复函数,I(jω)为i(t)的连续傅里叶变换;U(jω)为u(t)的连续傅里叶变换;Re[Z(jω)]为Z(jω)的实部。
由式(5)可知,当阻抗实部正定时,网络吸收的功率恒大于零,则单端口网络是无源的。
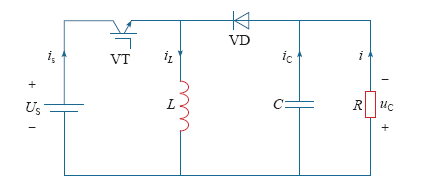
Buck-Boost变换器带恒阻负载如图3所示。
图3
图3
Buck-Boost变换器带恒阻负载
Fig.3
Buck-Boost converter with constant resistance load
由文献[9]可得Buck-Boost变换器工作在连续导电模式(Continuous Conduction Mode,CCM)情况下的状态方程为
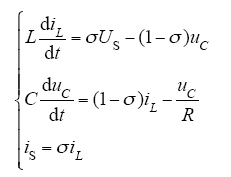
式中,L、C分别为电感和电容值;σ为驱动信号。
Buck-Boost变换器开环输入阻抗为
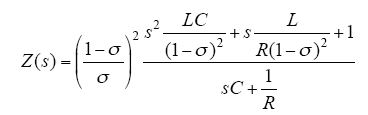
其实部为
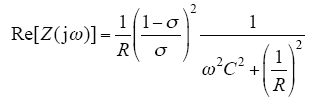
由式(8)可知,阻抗实部正定还是负定取决于R的正负,因此,当R为正时,阻抗实部正定,反之亦然。由CPL的负阻特性可知,R = RCPL = -UC2/P,即带CPL的Buck-Boost变换器输入阻抗实部负定,由实部负定可得带CPL的Buck-Boost变换器为非无源的,可导致其不稳定。
4 基于PCHD模型的无源控制
对于非无源Buck-Boost变换器,要保证其具有稳定性和优秀的稳态和动态性能,需设计无源控制器(Passivity Based Controller,PBC),使变换器变为无源的。对此,本文基于端口受控的耗散哈密顿(Port Controlled Hamiltonian with Dissipation,PCHD)系统模型设计PBC,克服CPL负阻特性影响。
4.1 端口受控耗散哈密顿系统
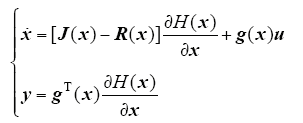
式中,x∈Rn为状态矢量;u,y为输入和输出矢量;R(x)为光滑依赖于x的半正定对称矩阵,R(x) = RT(x)≥0反映了端口上的附加阻性结构,表示系统的耗散;J(x)为n×n反对称矩阵,J(x) = -JT(x)反映了系统内部的互联结构。
在这种情况下,Buck-Boost能量平衡变成如下形式
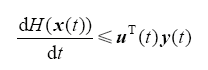
式(10)表明,如果哈密顿函数有下界,PCHD系统是严格无源的。
4.2 基于无源性PCHD系统控制思想
本文基于PCHD模型,采用互联和阻尼分配无源控制(Interconnection and Damping Assignment Passivity Based Control,IDA-PBC)方法进行PBC设计。
PCHD系统控制基本思想是为了使系统稳定在期望平衡点x*,保证系统的输出误差接近于零。给系统能量函数H(x)注入加入反馈控制后的能量函数Ha(x),生成新的期望能量函数Hd(x):Hd(x) = H(x) + Ha(x)。如果能够保证期望能量函数Hd(x)在平衡点x*处取极小值,即x* = argminHd(x),则这个状态的控制律u就能使系统工作在平衡点x*附近[11]。
IDA-PBC的控制思想是确定一个控制律u,使系统的闭环PCHD模型为
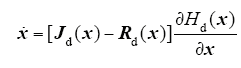
式中,Jd(x) = J(x) + Ja(x)和Rd(x) = R(x) + Ra(x)分别是新的互联和耗散矩阵;Ra(x)为阻尼注入矩阵;Hd(x) = H(x) + Ha(x)为总能量存储函数。
不失一般性,给定u,Ja(x),Ra(x)和矢量函数
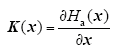
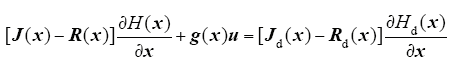
且使
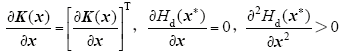
如果包含在集合A中的闭环系统最大不变集等于{x*},则系统将是渐进稳定的。
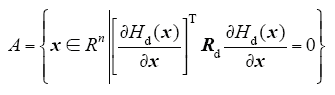
4.3 带CPL的Buck-Boost变换器PCHD模型
取电感磁链ϕL和电容电荷qC作为状态变量,即x = [x1,x2]T = [ϕL,qC]T。变换器的动态方程为
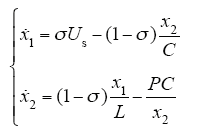
设变换器能量存储函数为
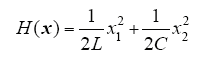
根据式(14)可得变换器的PCHD模型
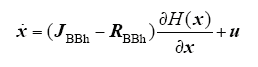
式中,JBBh,RBBh, 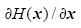
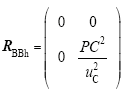
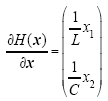
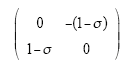
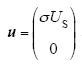
4.4 基于PCHD模型的Buck-Boost型变换器PBC设计
(1)期望平衡点的确定。根据动态方程式(14)可得期望平衡点
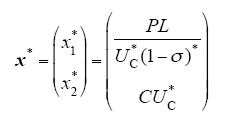
式中,UC*为满足CPL所需电压;σ*为期望驱动信号, 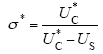
(2)PBC设计。设闭环系统形成的能量函数为
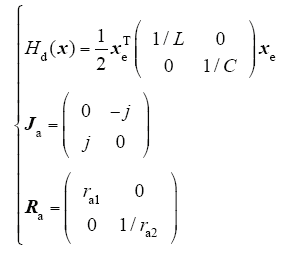
式中,j,ra1,ra2分别为系统的新增互联及阻尼注入参数;xe为误差。由式(18)可知,系统在x*处Hd(x)具有最小值。
根据IDA-PBC算法,K(x)满足
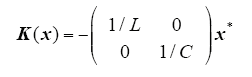
显然,满足可积性条件。
根据Hd(x) = H(x) + Ha(x)、Jd(x) = J(x) + Ja(x)、Rd(x) = R(x) + Ra(x),式(12)可变为
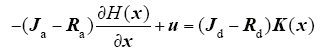
根据式(20)可得
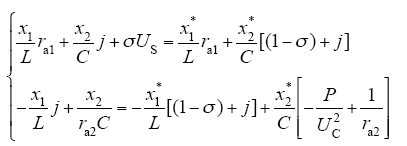
同时可得
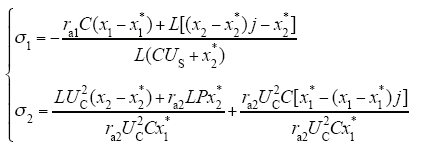
5 稳定性分析
结合无源控制律得到闭环控制输入阻抗为
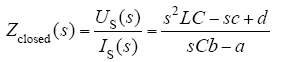
其阻抗实部为
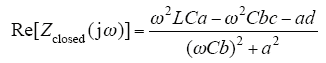
式中,a,b,c,d分别为
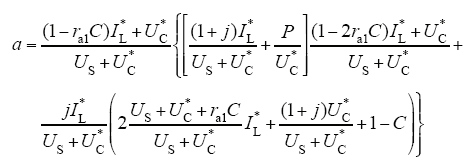
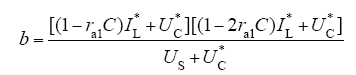
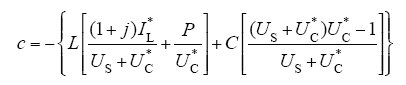
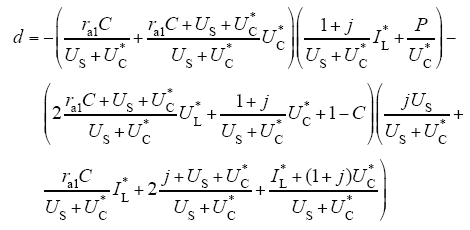
式(25)〜式(28)中,IL*、UC*分别为电压电流期望值;US为变换器输入电压;j为互联系数;ra1为阻尼系数。通过选择合适的j和ra1,可得a>0,b>0,c<0,d<0,得Re[Zclosed(jω)]>0,故阻抗实部正定,使施加PBC的带CPL的Buck-Boost变换器无源稳定。
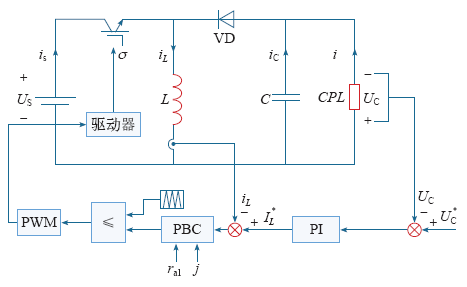
综上所述,构建Buck-Boost带CPL闭环控制原理框图,如图4所示。
图4
图4
Buck-Boost带CPL闭环控制框图
Fig.4
The closed loop control block diagram of Buck-Boost converter with CPL
6 仿真验证
表 仿真参数
Tab
| 参数 | 数值 | 参数 | 数值 | |
|---|---|---|---|---|
| Us/V | 200 | ra1 | 2 200 | |
| UC*/V | 200 | j | 80 | |
| L/mH | 500 | kp | 0.56 | |
| C/μF | 47 | ki | 120 | |
| P/kW | 1 | f/kHz | 10 |
图5
图5
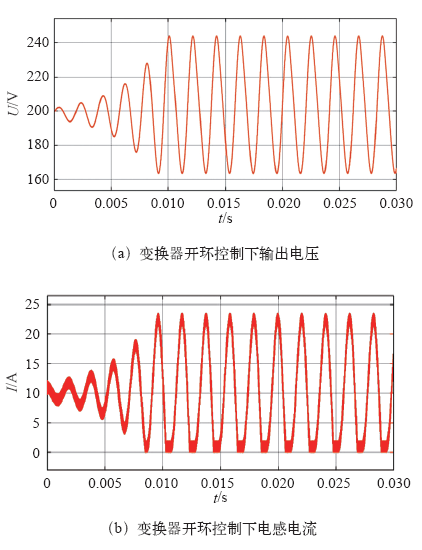
Buck-Boost带CPL开环控制状态
Fig.5
The open loop control state of Buck-Boost converter with CPL
图6
图6
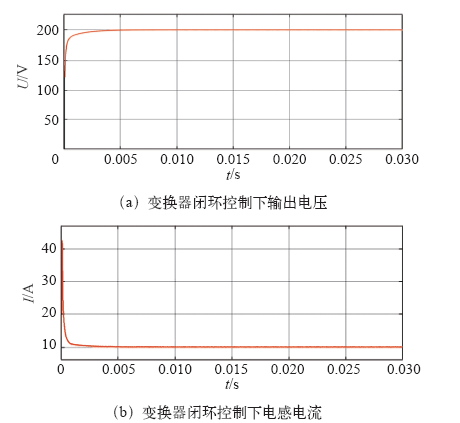
Buck-Boost带CPL闭环控制状态
Fig.6
The closed loop control state of Buck-Boost converter with CPL
7 结论
本文给出了CCM模式下Buck-Boost变换器带CPL的小信号模型,分析得出CPL的负阻特性使得变换器非无源的且可导致不稳定,因此本文利用无源控制来抑制CPL的负阻影响,使变换器无源和稳定。仿真结果表明,采用PBC可以使带CPL的Buck-Boost变换器输出稳定电压,可以有效地保证系统的动态响应和稳态运行。
参考文献
Modeling and analysis of a DC power distribution system in 21st century air lifters[D]. Department and Computer Engineering, Virginia Tech, Blacksburg,
Dynamics of a buck converter with a constant power load
[C].
An analytical investigation of DC/DC power electronic converters with constant power loads in vehicular power systems
[J].DOI:10.1109/TVT.2008.2010516 URL [本文引用: 1]
A Large-signal analysis of a DC-DC Buck power converter operating with constant power load
[C].
Global behavior analysis of a DC-DC boost power converter operating with constant power load
[C].
航天器直流电源系统稳定性分析方法研究
[J].
Research on the stability analysis strategy for spacecraft DC power system
[J].
A novel passivity-based stability criterion (PBSC) for switching converter DC distribution systems
[C].
DC/DC开关变换器的无源控制方法
[J].
Investigation of passivity-based control of DC/DC converter
[J].
基于DSP的能量双向流动交直流电源变换器
[J].