IGBT模块综合了MOSFET和双极性晶体管的优点,是目前轨道交通车辆变流器的核心器件。根据失效机理研究可知,由于封装中各层材料热膨胀系数不一致,IGBT模块在长期热循环冲击下可发生铝键合线断裂或脱落、焊料层老化、栅极氧化层损坏和芯片失效等^[1]。IGBT模块的失效可导致车辆机破事故而引起重大经济损失和不良社会影响,因此,IGBT模块的可靠性问题至关重要。

为预测IGBT模块的疲劳寿命,文献[2]基于模块各层材料变形量与结温波动的关系,得到了失效循环次数与结温波动的函数;文献[3,4,5,6]基于功率循环测试积累的参数,对不同影响因素进行分析,提出了相应的模块疲劳寿命模型。上述研究结果为计算IGBT模块疲劳寿命提供了数据基础,且使问题聚焦在获取IGBT模块工作过程中的瞬态结温波动曲线上。已有部分研究者将瞬态温升曲线与模块疲劳寿命模型相结合,应用于机车^[4,7]、电动汽车^[8,9,10]、风电^[11,12]等领域。

由于地铁线路的站点多、站间距短,车辆启停频繁,牵引逆变器的电气参数在不断变化,导致IGBT模块的损耗也在实时改变,加之走行风速有快有慢,热管散热器的散热能力相应发生变化,诸多因素使得地铁车辆牵引逆变器的IGBT模块结温波动非常复杂,给IGBT模块的疲劳寿命带来了严峻考验。为分析该问题,基于列车牵引、损耗、瞬态温升和疲劳寿命等理论方法进行了计算程序模块的实现,对北京地铁7号线牵引逆变器进行了IGBT模块的结温与疲劳寿命计算,并探讨了不同牵引策略、载荷工况、环境温度、接触热阻和疲劳寿命模型参数等因素对IGBT模块疲劳寿命的影响。

列车牵引计算研究作用在列车上的、和列车运行方向相平行的各种外力,如机车牵引力、列车阻力、列车制动力等与列车运行的关系^[13]。本文采用准确性高的多质点模型,先将每节车辆分别简化为一个质点再构成一个质点链,考虑列车编组对受力和牵引运行的影响。牵引策略可以决定列车运行的过程,列车牵引计算中较为常用的有最快速策略和最经济策略。最快速策略是列车尽可能地发挥其牵引性能和制动性能,限速路段采用限速匀速行驶,以最少的运行时间完成运行任务。最经济策略综合考虑实际运营对运行速度和时间的要求,在给定运行时分内采用最大牵引力加速至某一速度匀速运行,时间足够时惰行至终点,时间不够时惰行一段距离再用最大制动力制动。

列车牵引力通过电机提供的转矩经齿轮箱传递到列车轮对来驱动列车前进,阻力包括基本阻力、曲线阻力和坡道阻力,计算公式可见文献[13,14]。设电机功率因数为cosϕ,电机效率为η_m,逆变器效率为η_i,一台牵引逆变器给四台牵引电机供电,根据功率平衡关系和电机学知识计算电气参数为

电机输出功率

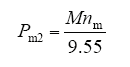
电机输入功率

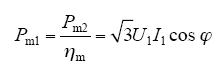
电机输入电流

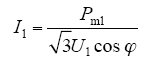
逆变器输出功率

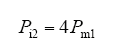
逆变器输入功率

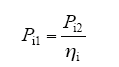
逆变器电流

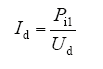
式中,M为牵引转矩;n_m为电机转速;U_d为中间电压。

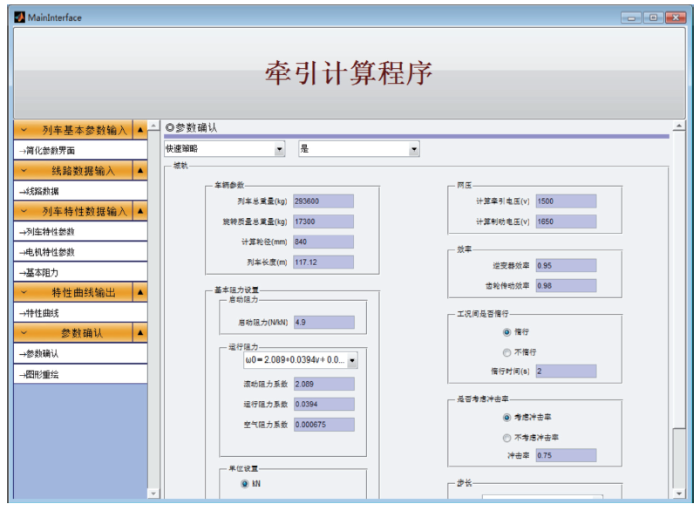
利用Matlab软件的M语言和GUI功能编写的牵引计算程序,如图1所示。车辆类型涵盖机车、动车组和地铁车辆,运行阻力包含了文献中已有的不同车型经验公式。

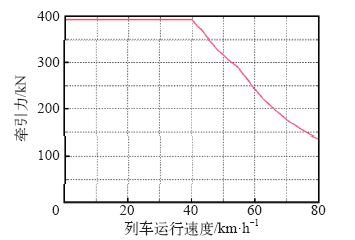
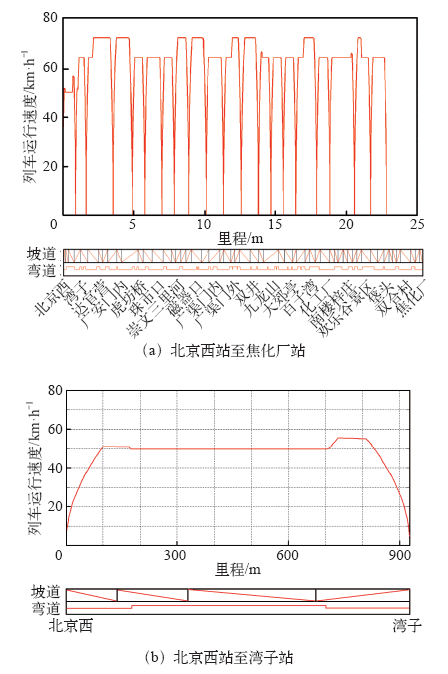
北京地铁7号线由北京西站至焦化厂站,全长约22.8km,共设车站21座。采用最大运行速度100km/h的车辆,车辆编组为Tc-M-M-M-M-Tc,Tc车质量为33t,M车质量为35t,整列车长度为117.12m,新轮直径为840mm,半磨耗轮径为805mm,齿轮传动比为6.312 5。座位坐满的载荷工况（AW1）为14.4t;额定载荷工况（AW2）是座位坐满及每平方米站6人（人均质量60kg）,为87.6t;超载工况（AW3）是座位坐满及每平方米站9人,为123.72t。额定载荷工况下,车轮在半磨耗状态,列车在干燥、清洁的平直轨道和额定网压下,列车牵引特性曲线如图2所示。

图3为二电平地铁车辆电气牵引系统的主电路原理图。电气牵引系统按照功能大致可分为高压电器及能量释放单元（1F01、QS₁、1Q02、F₁、VD₁和R₂）、电容器充放电单元（KM₁、KM₂、QS₁₁、R₁、R₃和R₄）、滤波单元（L和C）、电阻制动斩波及过电压抑制单元（斩波IGBT模块、1R01和1R02）、逆变器单元（变流器模块1和变流器模块2）、异步牵引电动机（1M01〜1M04）及检测单元（LH1〜LH8、VH1和VH2）等。这些功能单元基本上分属于高压电器箱、线路电抗器箱、制动电阻箱、牵引逆变器箱、牵引电机等不同设备中。图4为牵引逆变器结构示意图,可看出变流器模块在牵引逆变器箱中的位置。

利用牵引计算程序,依次设置车辆、线路数据和AW2载荷工况,计算步长取1m,旅行速度设为40km/h,选择最快速牵引策略,得到速度–里程曲线如图5所示。其中,图5a为北京西站至焦化厂站的速度–里程曲线,因站间距和不同里程上的坡道、弯道及限速有差异,导致不同里程上的列车速度有差异;图5b为北京西站至湾子站的速度–里程曲线,北京西站至湾子站的距离为927.3m,0~179.26m区间的限速为64km/h,179.26~674m区间的限速为49.9km/h,674~927.3m区间的限速为64km/h,列车先是加速启动,49.9km/h限速度段匀速运动,再加速和匀速运动,最后减速停靠湾子站。

图6为不同时刻对应的电气参数。其中,图6a为由北京西站至焦化厂站上行过程的电气参数曲线,整个上行时间需要2 335s（约39min,其中包含了各站点的停站时间30s）,该时间与北京地铁7号线实际运行时间40min较为接近;图6b为北京西站至湾子站的电气参数曲线,行驶过程耗时80s。牵引时的直流母线电压为1 500V,制动时因能量向电网回馈而导致直流母线电压为1 650V。列车加速与减速阶段的电机电流大,列车匀速运行时的电机电流小。IGBT模块的输出频率随电机转速而变化,即随列车速度的大小而相应变化。

IGBT模块由IGBT芯片和反并联快速恢复二极管芯片组成,其损耗为二者的导通损耗与开关损耗之和。目前,二电平变流器的损耗计算方法较为成熟且统一,许多半导体器件厂商开发了易于使用的损耗计算工具,如Infineon公司的IPOSIM、ABB公司的Simulation-Tool、Semikron公司的SemiSel、Mitsubishi公司的Melcosim和Fuji公司的IGBTSim等。IPOSIM软件采用的假设及处理方式具体为：①电路为上下桥臂对称的三相桥式拓扑结构;②输出电流为正弦波;③采用SPWM双极性调制;④输出特性采用线性化近似;⑤IGBT芯片开通和关断一次损失的能量基本与电流和直流母线电压成正比;⑥忽略二极管芯片的开通损耗;⑦利用电流和直流母线电压修正二极管芯片关断一次损失的能量;⑧利用产品数据手册提供的结温25℃和结温125℃的参数进行插值处理来考虑结温对损耗的影响。二电平变流器的IGBT模块损耗计算公式可见文献[15]。

针对三电平变流器的IGBT模块损耗计算,可根据开关状态和换流路径得到中性点钳位（Neutral Point Clamped,NPC）和有源钳位（Active Neutral Point Clamped,ANPC）等主电路拓扑的损耗计算公式^[16]。利用Matlab软件的M语言编写损耗计算模块,集成封装了文献中的计算公式和半导体器件厂商提供的大部分IGBT模块数据手册参数。

以图6所示的电气参数为输入,IGBT元件的开关频率取500Hz,利用损耗计算模块可以得到不同时刻的损耗数据,如图7所示。其中,图7a为北京西站至焦化厂站的IGBT模块损耗曲线;图7b为北京西站至湾子站的IGBT模块损耗曲线。列车加速时,IGBT损耗大;列车减速时,二极管损耗大;列车匀速时,IGBT损耗和二极管损耗均较小。

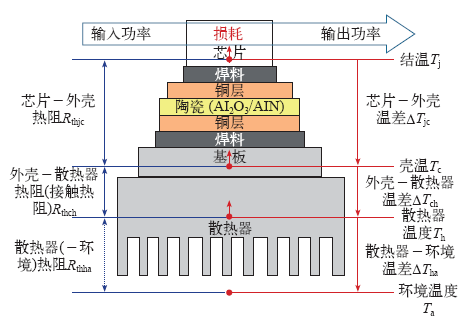
为保证IGBT模块的工作可靠性,实际工程应用中的IGBT模块会被安装在某种类型（如翅片风冷、水冷、热管冷却、冷媒等）的散热器上,相应的传热模型如图8所示。由芯片损耗产生的热量依次通过封装材料和散热器传递到空气中,最终达到热平衡。利用热阻和损耗计算公式,可以得到相应的稳态温度。

利用热阻抗,可以计算t时刻的散热器瞬态温度为

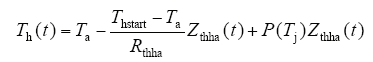
式中,T_a为环境温度;T_hstart为散热器初始温度;R_thha为散热器热阻;Z_thha(t)为t时刻的散热器热阻抗;P(T_j)为结温为T_j时IGBT芯片和二极管芯片的损耗之和。

瞬态平均结温为

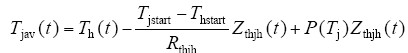
式中,T_jstart为芯片结温初始温度;R_thjh为芯片至散热器的热阻;Z_thjh(t)为t时刻芯片至散热器的热阻抗。

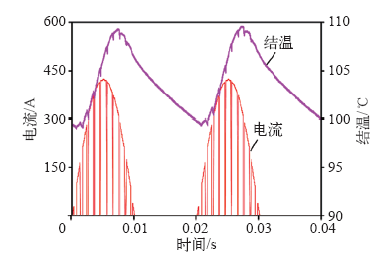
实际上,输出电流的正半周通过IGBT芯片时,IGBT芯片损耗近似为半正弦波,而二极管芯片的损耗为0;输出电流的负半周通过二极管芯片时,二极管芯片损耗亦近似为半正弦波,而IGBT芯片的损耗为0,这种损耗的特性会使得芯片结温产生波动,如图9所示,锯齿的产生由脉宽调制引起。输出频率较低时（如小于5Hz时）,结温波动的影响将变得很明显。

考虑损耗波形和输出频率对结温波动的影响,采用半正弦波损耗的假设进行修正后的瞬态最大结温为

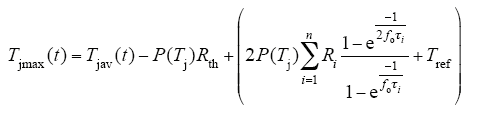
式中,f_o为输出频率;T_ref为参考温度（IGBT模块无基板封装时,T_ref等于散热器温度;IGBT模块有基板封装时,T_ref等于IGBT模块壳温）;R_th为芯片至散热器的热阻（IGBT模块无基板封装时）或芯片至壳的热阻（IGBT模块有基板封装时）。

因采用了半正波损耗的假设,会将原有两个时刻之间分成与输出频率相关的多个时间子步,弥补了因电流基波平均损耗而丢失的大量结温波动信息,此过程需要消耗较长的计算时间。又因损耗与温度互相耦合,需要对上述公式进行大量的迭代计算,才能得到相应的结果^[17]。利用Matlab软件的M语言编写了瞬态温升计算模块,可以迭代调用损耗计算模块。

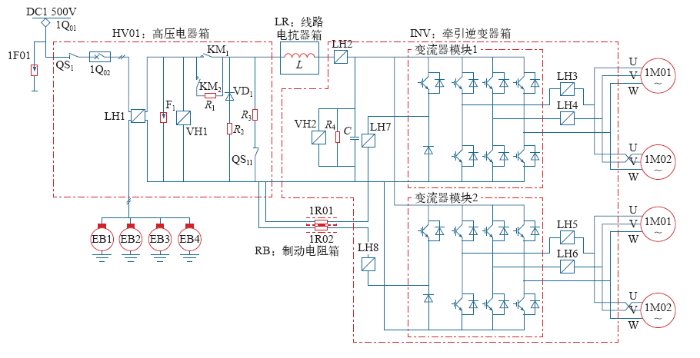
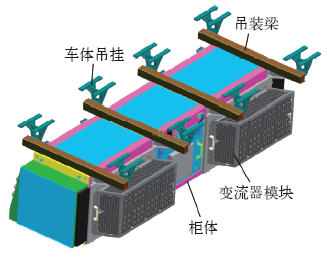
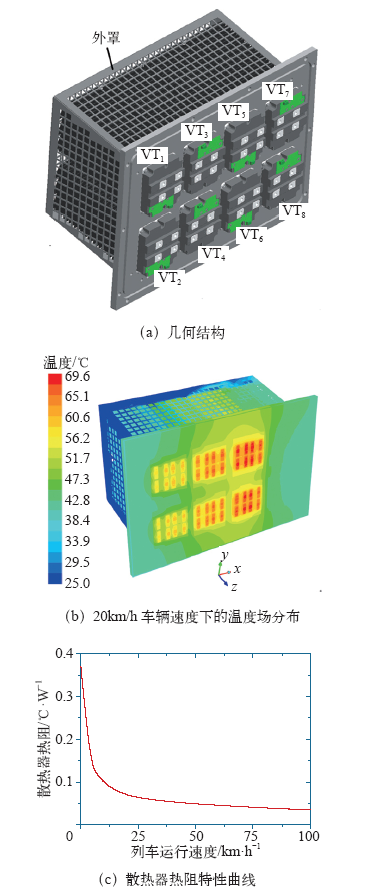
北京地铁7号线地铁车辆牵引逆变器采用热管散热器加走行风冷方式进行散热,如图10所示。其中,图10a为热管散热器的几何结构,热管散热器上安装了8个IGBT模块,VT₁~VT₆实现三相逆变功能,VT₇和VT₈实现过电压抑制斩波功能。由于斩波是在网压高于规定值时工作,产生的短时间损耗会对其他IGBT模块的结温有不同程度的影响,为简化具有较大随机性的斩波行为带来的复杂问题,假设斩波相一直处于不工作状态。通过数值模拟方法^[18]可以得到如图10b所示的某一车辆速度下的热管散热器温度场分布,不同的IGBT模块因所处位置散热性能差异而导致热阻值有所不同。为简化分析,取温度最高的VT₅元件进行研究,以环境温度、VT₅元件的发热量及对应热管散热器安装面上的温度来计算该IGBT模块的散热器热阻。通过提取不同车辆速度下的数值模拟结果可绘制出如图10c所示的散热器热阻特性曲线。列车速度为0时,热管散热器处于自然对流状态,随着车辆速度的增加,散热器热阻下降特点为先急剧后缓慢。由于散热器热阻特性曲线表现出明显的非线性,式（7）~式（9）中的散热器热阻应依据不同时刻的车辆速度所对应的散热器热阻值来计算。散热器时间常数可根据瞬态数值模拟得到的温升曲线或温升试验来确定。

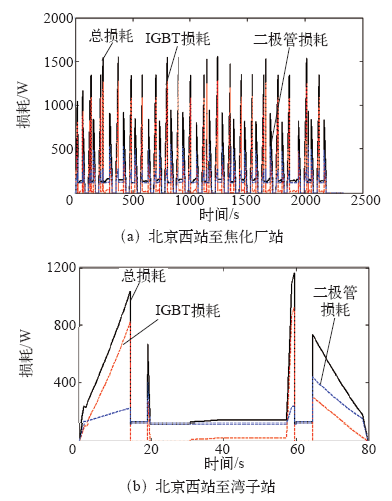
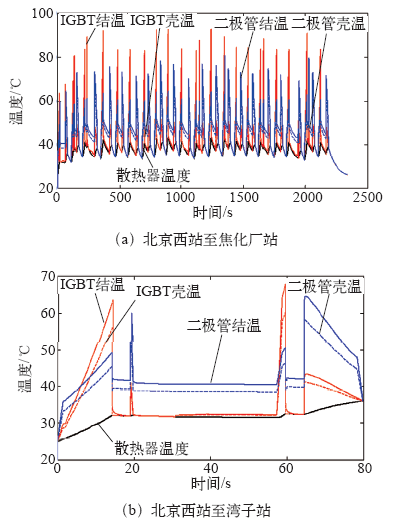
图11为环境温度设置为25℃、IGBT模块与散热器之间的接触热阻为0.02W/K时,通过瞬态温升计算模块得到上行过程中不同时刻的IGBT结温、二极管结温、IGBT壳温、二极管壳温和散热器温度。其中,图11a为北京西站至焦化厂站的温升曲线,因列车加速和减速阶段的损耗大,IGBT结温和二极管结温的数值较大。列车运行过程中,IGBT结温和二极管结温相对于环境的最大温升值分别为67.69℃和56.01℃;图11b为北京西站至湾子站的温升曲线,可以清楚地看出IGBT结温、二极管结温、IGBT壳温和二极管壳温的变化受损耗的影响非常大,损耗增大时的温度迅速升高,损耗减小时的温度迅速降低,散热器温度的变化则因距离芯片较远且时间常数较大而波动较小。

在得到不同时刻的IGBT结温、IGBT壳温、二极管结温、二极管壳温、焊料层温度和散热器温度的基础上,结合IGBT模块疲劳寿命模型、雨流计数法和线性累积损伤理论进行叠加,最终可以得到循环载荷产生的总损伤。雨流计数法和线性累积损伤理论相对简单,准确计算IGBT模块疲劳寿命的关键是确定合适的疲劳寿命模型与参数。

疲劳寿命模型可分为解析模型和物理模型两大类。解析模型由老化数据的拟合得到,表达直观,但没有体现老化试验变量的物理关系,主要有简单Coffin-Manson模型、LESIT模型、Norris-Landzberg模型、Bayerer模型等;物理模型通过材料应变分析和老化数据结合得到,可深层次地反映影响疲劳寿命的物理机理,但表达式复杂且难于获取,主要有基于应变的模型、基于开裂机理的模型和基于能量的模型等。

简单Coffin-Manson模型只考虑了循环中结温波动量ΔT_j的影响,只适用于温度波动小于120℃的情况,且精度不高。

对不同厂家采用标准工艺封装的模块进行大量试验测试,在同时考虑结温波动量和温度平均值情况下总结出的LESIT模型为

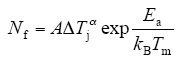
式中,A和α为常数;E_a为激活能;k_B为波尔兹曼常数;T_m为温度循环的平均温度,K。

Norris-Landzberg模型认为焊料层的疲劳受周期时间和形状（温度保持时间、上升下降时间）的影响,可将式（10）修正为

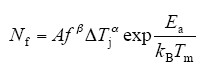
式中,f为循环频次;β为试验数据拟合的常数。

Bayerer模型除考虑最大温度与温度波动量,还考虑了升温时间、负载直流电流、键合线直径和模块的耐压值等,是目前考虑变量最多的解析模型,然而该模型的参数只适用于绝缘基片（substrate）材料为Al₂O₃的模块,而不适用于绝缘基片材料为AlN和AlSiC的模块。本文利用Matlab软件的M语言编写了集成不同疲劳寿命模型的疲劳计算模块。

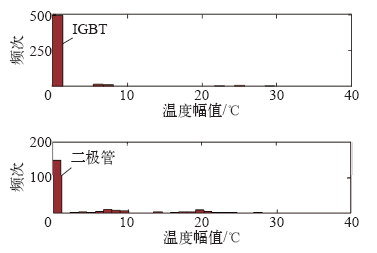
根据图11a所示的北京西站至焦化厂站温升曲线,选择LESIT模型及一组参数：A = 640,α = -5,E_a/k_B = 9 381.8,利用疲劳寿命计算模块进行计算得到雨流幅值循环分布如图12所示,可以看出不同温度幅值对应的频次。经过计算可知,单次上行的IGBT芯片平均温度为41.77℃,疲劳损伤为5.316×10^-8,二极管芯片平均温度为46.41℃,疲劳损伤为2.263×10^-8。尽管IGBT芯片平均温度低于二极管芯片,但IGBT芯片结温的波动幅度要大于二极管芯片结温,使得IGBT芯片的损伤比二极管芯片大。按照上述方法,计算从焦化厂站到北京西站的下行工况,所需时间为2 338s,芯片平均温度与损伤基本一致。地铁车辆折返时间为120s,每天上下行次数取11次,按运行20年、每年365天来计算,可知IGBT芯片总体疲劳损伤为0.008 5,二极管芯片总体疲劳损伤为0.003 6,这些值均远小于1,较大程度上得益于芯片平均温度较低,由此可知IGBT模块的疲劳寿命裕量大。文献[7]将HXD1C机车一天的运行周期等效为启动加速、恒速、重载爬坡、爬坡和停车等工况,分别利用LESIT模型、Norris-Landzberg模型和ABB模型进行了疲劳寿命预估,认为ABB模型增加了环境温度的影响,其预测值与实际工作寿命更加接近。文献[9]结合大量功率循环测试的数据,将某混合动力电动汽车在运行曲线下的瞬态温升数据转换为任务循环的次数,进而计算出IGBT模块的使用年限。文献[12]利用马尔可夫链模型处理风电变流器的随机工作过程,再利用雨流计数法对IGBT模块瞬态结温数据进行疲劳寿命预估。由于地铁车辆运行具有正点率高的特点,基于牵引计算获得的电压、电流、输出频率和功率因数等电气参数比等效运行周期和随机工作过程更加符合实际情况,因此,本文的计算过程更为合理。同时,图12为地铁车辆在线路上运行时表现出的IGBT和二极管芯片温度幅值分布,其特点较图6、图7和图11更为简洁明了,有利于用简单的数据描述复杂的现象,后续可以针对地铁车辆在不同线路、不同条件下得到的IGBT和二极管芯片温度幅值分布总结其变化特点及规律。

上述计算的最快速牵引策略最大化利用了牵引力与制动力,IGBT模块的损耗大,温升相应较大。采用最经济策略进行计算时,设置旅行速度为35km/h,上行需要2 348s。环境温度设置为25℃,接触热阻设置为0.02W/K,选择LESIT模型计算出IGBT芯片平均温度为41.06℃,疲劳损伤为5.06×10^-8,二极管芯片平均温度为46.18℃,疲劳损伤为2.047×10^-8。这是由于最经济策略尽可能利用了惰行,IGBT模块的损耗有所降低,使得芯片平均温度与损伤小于最快速牵引策略的计算结果。

采用AW3工况和最快速牵引策略,环境温度为25℃,接触热阻为0.02W/K,选择LESIT模型计算可知IGBT芯片平均温度为43.35℃,疲劳损伤为1.444×10^-7,二极管芯片平均温度为47.63℃,疲劳损伤为3.213×10^-8。随着载客人数的增加,牵引逆变器需输出更大的电流,导致IGBT模块损耗相应增加,芯片平均温度和疲劳损伤也相应增大。

采用AW3工况和最快速牵引策略,接触热阻为0.02W/K,环境温度由25℃改为40℃,通过LESIT模型计算可知,IGBT芯片平均温度为58.36℃,疲劳损伤为5.532×10^-7,二极管芯片平均温度为62.63℃,疲劳损伤为1.19×10^-7。随着环境温度的提高,芯片平均温度提高,IGBT模块损耗稍有增加,而芯片的疲劳损伤则有较大幅度增大,这说明了IGBT模块的散热条件对疲劳寿命有很大影响。

采用AW3工况和最快速牵引策略,环境温度为40℃,IGBT模块与散热器之间的接触热阻由0.02W/K改为0.2W/K,通过LESIT模型计算可知,IGBT芯片平均温度为95.51℃,疲劳损伤为0.162,二极管芯片平均温度为129.36℃,疲劳损伤为0.285。随着接触热阻的增大,芯片平均温度大幅度提高,芯片的疲劳损伤急剧增大,说明接触热阻对IGBT模块的散热与疲劳寿命有非常大的影响,实际应用中需要特别注意导热硅脂干涸和性能恶化的情况。

文献[19]认为不同的厂家和类型的IGBT模块测试参数有差异,得到一款IGBT模块疲劳寿命模型参数为：A = 12.880 4,α = -2.529 5,E_a/k_B = 6 022.9。采用AW3工况和最快速牵引策略,环境温度为40℃,接触热阻为0.02W/K,通过计算可知IGBT芯片平均温度为58.36℃,疲劳损伤为1.396×10^-4,二极管芯片平均温度为62.63℃,疲劳损伤为5.482×10^-5,均高出前一组疲劳寿命模型参数计算出的IGBT芯片和二极管芯片损伤两个数量级。说明IGBT模块的疲劳寿命模型参数发生变化时,计算出的疲劳寿命结果也会发生较大变化,选择合适的疲劳寿命模型与参数是准确预估IGBT模块疲劳寿命的关键。

本文提出了一种计算地铁车辆牵引逆变器IGBT模块结温与疲劳寿命的方法,进行了列车牵引、损耗、瞬态温升和疲劳寿命等计算程序模块的开发。以北京地铁7号线为例进行计算与分析,发现电气参数的变化与线路条件、牵引策略等有很大的关系,IGBT模块的损耗和结温变化情况非常复杂,进而影响到IGBT模块的疲劳寿命。

不同的运行策略对列车的电气参数影响很大;停站时间和惰行时间会对温升变化曲线产生一定影响;斩波制动时斩波相的元件会产生热量,导致散热器上的温度分布明显不均;热管性能、散热片积灰、导热硅脂老化和安装紧固状态的好坏会严重影响散热性能;不同的主电路方式、控制策略、网压波动、电流谐波会导致损耗波形并非光滑的半正弦波;现有的结温进行了平均化处理,实际的芯片温度场分布是不均匀的,采用模型降阶法计算瞬态温度场的精度接近有限元法,效率高出有限元法数百至数千倍,使得快速准确计算实际几何结构不同部位的瞬态温升结果成为可能^[20];IGBT模块失效主要有键合线断裂或脱落、焊料层老化和芯片失效等,现有IGBT模块的疲劳寿命模型在精度与通用性上存在一定局限性,利用不同IGBT模块疲劳寿命模型及参数计算出的结果有较大差异;动车组和电力机车与地铁车辆的运行机制大致相同,可应用列车牵引计算程序模块得到随运行条件变化的电气参数,进而计算IGBT模块的损耗、瞬态温升和疲劳寿命。以上诸多复杂的因素及问题,均可结合本文所述方法进一步开展相关研究。