1 引言
国家经济的稳步发展,离不开电力系统的支持。社会生活的方方面面也与电力系统息息相关。在电力行业“十二五”规划的指导下[1],现有电网的电压等级不断提高,装机容量持续增长。伴随而来的,是用户对用电可靠性的进一步要求,这也给电力设备的运行管理提出了更高的要求。
高压断路器作为电网中起保护和控制作用的设备,其运行状态将直接影响整个电力系统的稳定性和供电的可靠性。断路器的故障失效,使得本应由其保护的线路或设备面临严重损坏的风险。而且由于断路器未及时发挥其保护作用,很可能使电网事故扩大,造成大面积停电,给生产、生活带来重大的经济损失[3]。现有确保断路器稳定运行的手段就是检修,但是频繁的检修不仅会使设备维护的人力成本大大增加,而且会带来不必要的停电,在不规范的解体组装操作中还极易引入二次损坏。因此,如何在保证断路器正常运行的前提下,实时掌握断路器的健康状态,尽可能地减少检修次数,是设备管理单位关心的内容。
2 基准态评估
为了更好地掌握设备的运行状态,需要有一个指标客观地反映设备当前的健康情况是否能满足所处电网的要求。本文及文献《输变电设备智能化运维系统研究与应用》[1]均为深圳供电局有限公司及国网电力科学研究院武汉南瑞有限责任公司基于项目“全维度设备状态监测中心关键技术研究”的研究成果。本文作为前文研究的延续,基于前文中提到的“基准态”概念,构建出针对在运设备全方位多角度的评价体系。
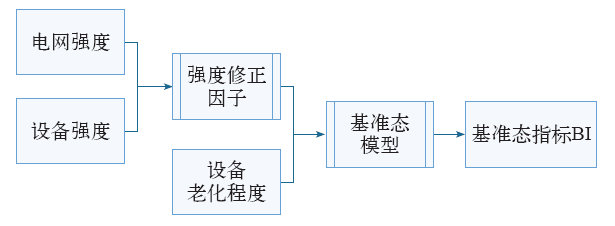
所谓基准态是指设备在电网及自身的强度要求下,指定的设备所有规定性能均维持正常运行的状态。本定义有以下方面的涵义:一是“强度要求”包括电网强度和设备强度,即“通过设计参数、结构特点和制造工艺等评估设备强度,利用过电压、过负荷和短路冲击等不良工况评估电网强度”;二是“所有规定性能维持正常运行”包括高压断路器机械性能、电气性能、绝缘性能和附件性能[4]都能维持正常运行;三是前两个条件对基准态来说,缺一不可,互为补充,但设备基准态并不是固定不变的,当强度提高要求到一定程度,或设备部分规定性能并不能维持正常运行时,其基准态也会随之而变。为了对设备进行可靠性分析,首要步骤就是利用基准态的概念评估设备当前状态,基准态评估流程如图1所示。
图1
2.1 状态量分析
(1)电网强度。所谓电网强度,即指设备在电网中所处位置的环境及运行条件的情况。其中,环境条件如温度和湿度等,过高的温度或高湿的环境都会减少断路器的运行寿命;运行条件如变电站中性点接地情况的不同,导致线路在发生接地故障时的短路电流的大小,从而也会影响断路器的运行寿命。以基准态为核心的可靠性分析的目的就是要确保设备状态高于设备所在地电网强度的要求,并通过有效的手段,调节设备与电网强度之间的关系。表1中给出了反映电网强度的状态量指标及其评估依据。
表1 电网强度状态量评价
Tab.1
| 序号 | 类别 | 状态量 | 评估依据 | 权重k | 评分s |
|---|---|---|---|---|---|
| 1 | 环境 因素 | 温度 | 年平均气温,极热/极寒天数 | 2 | 1,2,3 |
| 2 | 湿度 | 空气湿度百分比 | 2 | 1,2,3 | |
| 3 | 污秽度 | A、B、C、D级 | 3 | 1,2,3 | |
| 4 | 安装位置 | 室外或室内 | 1 | 1,3 | |
| 5 | 距海岸距离 | 考虑海滩与非海滩的区别 | 3 | 1,2,3 | |
| 6 | 雷电密度 | 区域落雷情况,次/(km2·年) | 3 | 1,2,3 | |
| 7 | 环境种类 | 是否靠近工业区、坟场、发电厂等 | 1 | 1,2,3 | |
| 8 | 运行 因素 | 中性点接地情况 | 直接接地、低阻接地、非有效接地 | 3 | 1,2,3 |
| 9 | 计算短路电流 | 额定开断短路电流值是否满足安装地点最大运行方式下短路电流,以及是否采取了防范措施 | 5 | 1,2,3 | |
| 10 | 是否开合空载长线 | 是或否 | 2 | 1,3 | |
| 11 | 是否有人值守 | 是或否 | 1 | 1,3 |
其中,评分s为状态量依据评估条件进行的评级,分为1,2,3三种情况,3分表示情况最好,1分表示情况最差。权重k为该状态量的加权程度,依据影响程度分为1~5五个等级,5分表示影响最大,1分表示影响最小,具体分值可依据供电局实际检修记录资料统计和专家经验得出。从而,某设备的电网强度指标Igrid定义为各状态量评分的加权和,即
(2)设备强度。设备强度综合从设备在线监测装置安装情况、缺陷故障因素和自然因素角度评价在运设备的抗风险能力,具体的状态量指标及其评估依据见表2。
表2 设备强度状态量评价
Tab.2
| 序号 | 类别 | 状态量 | 评估依据 | 权重k | 评分s |
|---|---|---|---|---|---|
| 1 | 在线监测装置安装 | 在线监测装置安装情况 | 共安装几类,是否正常运行 | 1 | 1,2,3 |
| 2 | 缺陷故障因素 | 历史缺陷记录 | 发生次数,是否处理 | 4 | 1,2,3 |
| 3 | 历史故障记录 | 发生次数 | 5 | 1,2,3 | |
| 4 | 家族性缺陷 | 是否存在,缺陷级别,是否整改 | 3 | 1,2,3 | |
| 5 | 同型设备缺陷情况 | 是否存在,缺陷级别 | 3 | 1,2,3 | |
| 6 | 自然因素 | 地震 | 是否发生过 | 2 | 1,3 |
| 7 | 受潮 | 是否发生过 | 2 | 1,3 |
同上,该设备的设备强度指标Idevice为各状态量评分的加权和。
(3)设备老化程度。设备老化程度从设备的机械、电气和绝缘性能评估设备本体,再辅以附件性能评估,综合得到设备的老化程度,具体的状态量指标及其评估依据见表3。
表3 设备老化程度状态量评估
Tab.3
| 序号 | 类别 | 状态量 | 评估依据 | 权重k | 评分s |
|---|---|---|---|---|---|
| 1 | 机械性能 | 运行年限 | 投运年限 | 3 | 1,2,3 |
| 2 | 时间速度特性曲线 | 合(分)闸时间、合(分)闸同期、合(分)闸速度等 | 5 | 1,2,3 | |
| 3 | 触头机械寿命 | 故障分闸次数、正常分闸次数 | 5 | 1,2,3 | |
| 4 | 电气性能 | 分合闸线圈 | 合(分)闸线圈电流波形、合(分)闸线圈直流电阻、操作电压 | 5 | 1,2,3 |
| 5 | 触头电寿命 | 触头相对磨损量 | 5 | 1,2,3 | |
| 6 | 静态回路电阻 | 主回路电阻值 | 5 | 1,2,3 | |
| 7 | 动态回路电阻 | 计算弧触头长出主触头的长度 | 5 | 1,2,3 | |
| 8 | 绝缘性能 | 局部放电 | 是否发生、发生次数 | 3 | 1,2,3 |
| 9 | 绝缘介质状态 | SF6气体的成分、密度、湿度 | 4 | 1,2,3 | |
| 10 | 一次回路对地绝缘电阻 | 阻值是否过小 | 5 | 1,2,3 | |
| 11 | 辅助和控制回路绝缘电阻 | 阻值是否过小 | 4 | 1,2,3 | |
| 12 | 附件性能 | 操作机构 | 储能机构、二次元件、脱扣器、加热除湿装置、排污装置等 | 3 | 1,2,3 |
| 13 | 合闸电阻 | 阻值、温度、外绝缘情况等 | 5 | 1,2,3 | |
| 14 | 均压电容 | 介损、电容量、温度、外绝缘情况等 | 5 | 1,2,3 |
同上,该设备的设备老化程度指标Iage为各状态量评分的加权和。
2.2 基准态计算
(1)强度修正因子。考虑到处于同一老化程度的设备,在不同的电网强度及设备强度的要求下,其可靠性评估的程度也不一样。为了解决上述问题,通过电网强度和设备强度的评估结果,构建了强度修正模型,得到设备的强度修正因子F。通过强度修正因子F不仅可以对设备的老化评估进行修正,同时还可以根据强度修正因子的大小排序,挑选出强度修正因子较大设备进行重点关注。
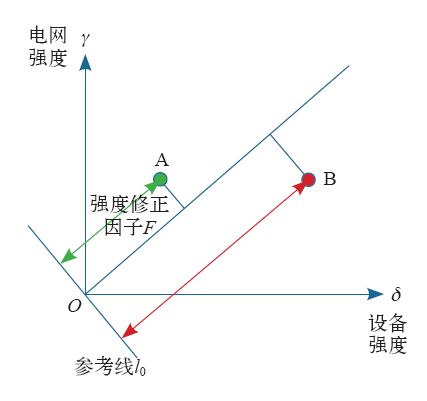
强度修正模型如图2所示。规定参考线l0的方程式为:x + y = 0;γ、δ为断路器的电网强度和设备强度评分的归一化结果(由实际得分除以最大的条件得分而来),则某断路器A在δ - γ坐标系中的坐标为(δA,γA),其中0≤δA≤1、0≤γA≤1;定义断路器A的强度修正因子F为该点到参考线的距离,即
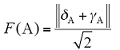
图2
对式(2)进一步归一化得到
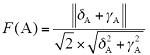
归一化后 的取值范围是[0,1],当设备电网强度和老化强度得分较高时,F趋近于1,利用其对设备的老化评估结果进行修正时,将不会产生较大的影响。反之,设备电网强度和老化强度得分较低时,F趋近于0,修正后的老化评估分数将大为降低。
(2)基准态模型。在计算设备基准态前,首先需要先将设备的老化程度指标映射到百分制,以方便将设备进行横向对比,映射公式为
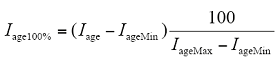
式中,Iage100%为百分制的老化程度指标;IageMin为老化程度指标理论最小值;IageMax为老化程度指标理论最大值。
随后,将百分制指标Iage100%乘以强度修正因子F,即可得到设备基准态值BI = Iage100%×F。BI也为百分制指标,100分代表设备当前状态非常好,0分表示设备已经报废。
3 基准态预测
在基准态分析中对设备进行了参数归类、分性能评估,根据分性能评估结果之间的逻辑关系,对各分性能基准态值进行综合计算,从而得出能够表征断路器整体状态的、单一的设备基准态值BI。BI能全面、有效地衡量当前设备的运行状态,可以为检修决策提供依据。
但从数据的监测或检测到计算出设备基准态值存在一定的时间滞后。于是,当发现设备基准态值发生偏移,然后再采取相应的检修或更换措施,很有可能设备已经出现明显缺陷,甚至发生故障,这不但影响设备的使用寿命,还会给电力系统带来潜在的危险。如果能对不同寿命阶段设备基准态值BI进行预测,就能知道设备状态在设备全寿命周期内的变化趋势,在缺陷、故障发生之前就能提前对它采取预防措施,这不仅能延长设备的使用寿命,还能大大提高整个电力系统的运行可靠性。
基准态预测就是在设备基础态分析的基础上,对设备基准态值BI与设备运行年限的关系进行分析,建立相应的数学模型,得到设备状态轨迹。根据调研及统计分析可知,设备基准态随着服役年限的增加呈下降趋势,刚投入运行时的状态最好,随着时间推移,状态越来越差,整体变化基本上呈指数分布的形式。本文参考英国EA公司的健康指数计算公式的原理,引入状态衰减系数,提出基于基准态的设备健康水平指数随时间变化过程的一个经验公式,即
式中,BIt1为设备在未来t1时刻的基准态指标值;BIt0为设备t0时刻的基准态指标值;h为状态衰减系数;B为老化系数;t1为所要计算的BIt1对应的年份,可为当前年份,也可为未来年份;t0为全新设备BIt0对应的年份,一般为设备投运年份。
4 可靠性分析
4.1 故障率模型
从基准态的定义可知,一旦BI值较低,设备出现故障的概率就会增加。设备故障的发生概率直接反映出设备运行的可靠程度,因此对设备进行可靠性分析的首要一步就是确定设备故障率。
本文参考相关资料,认为当设备状态恶化时,设备发生故障的概率会以指数级增加[7],这趋势也与现场经验相一致。因此,提出如下概率模型
式中,BI为本文所提到的设备基准态值,代表设备状态的量化指标;故障模型中所述之概率,含义为“在某个时间点t后的单位时间Δt内,由于设备状态的改变,设备发生故障的概率”,这与故障概率密度的经典定义相一致,因此P表示的概率即为故障概率密度(取值范围0~1);K与C分别为比例系数和曲率系数,是与设备种类、运行环境等诸多因素有关的常量,没有明确的直接获取方法,通常可通过反演计算得出;假设当前有一批状态和故障样本数据,其中基准态分类BI有1~N种,对应的设备台数为M1~Mn,在一个历史评估周期内故障台数为Q,则根据上述公式,应满足
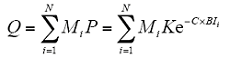
这样就得到了关于K和C的一个方程。如果有两年以上的数据,即该方程已知两组以上的解,就可以通过最小二乘法等算法拟合方程,从而求得K和C。
4.2 可靠性模型
在计算得到设备故障率后,要计算设备的可靠性,首先需明确可靠性函数R(t)和累积故障分布函数F(t)的定义[8]:R(t)指在时刻t还没有故障的产品数除以总数;F(t)指在时刻t已经故障的数目除以总数。根据以上定义可知
对F(t)求导,就能得到“在某一时刻t后的单位时间Δt内故障发生概率,也就是Δt内故障数除以总数”[9],定义为故障密度f(t)。即
f(t)反映了故障概率密度,即相对于产品总体数量,在其中某一年发生的故障多少,即等同于上节中的故障概率密度P。因此,可靠性函数与故障概率密度之间的关系为
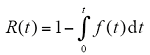
代入4.1节中得到的可靠性模型有
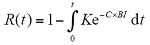
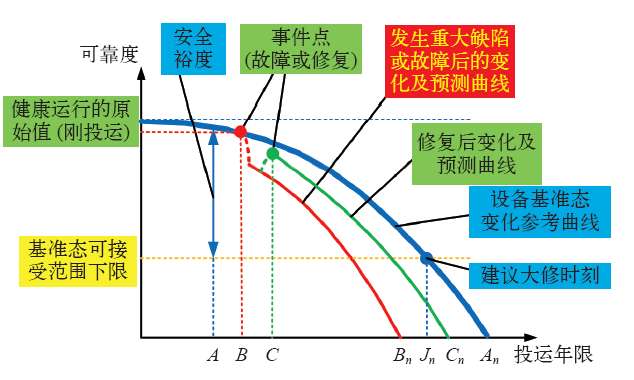
图3
(1)蓝色为参考曲线,为该划分类中设备的基准态变化规律。其中,任何投运年的基准态分析结果与基准态可接受范围下限的差值表示该设备安全运行裕度,当设备的安全裕度为0时,该下限与设备基准态变化曲线的交点所在的年份(如图中Jn点)即为设备大修或更换时间点。
(2)红色曲线为假设某设备发生某故障或缺陷后,从事件点(B时刻)开始其基准态变化曲线的突变情况,以及因此对其寿命、大修时刻等的影响。
(3)绿色曲线为假设C时刻对设备进行检修,使得其基准态分析结果跃升一定的水平,并由此对设备的未来状况进行预估。
(4)An、Bn、Cn分别为设备通常的使用寿命、经历故障或缺陷后的使用寿命与检修恢复后的使用寿命。
5 方法实践
统计某一型号断路器在不同运行年限和对应的设备基准态值BI见表4。
表4 设备基准态值
Tab.4
| 运行年限 | BI |
|---|---|
| 1 | 94.7 |
| 2 | 94.3 |
| 5 | 93.2 |
| 8 | 91.7 |
| 10 | 90.5 |
| 15 | 86.3 |
| 18 | 81.7 |
| 20 | 77.2 |
| 22 | 71.8 |
| 25 | 62.3 |
| 27 | 56.8 |
| 30 | 49.7 |
结合表4中数据,拟合式(5)所述曲线,得出状态衰减系数h = 0.045 37,老化修正系数B = 0.053 63。在这里定义全新设备(刚投运t0 = 0)的性能指标值为95,即BIt0 = 95,则最终确定该设备基准态预测模型为
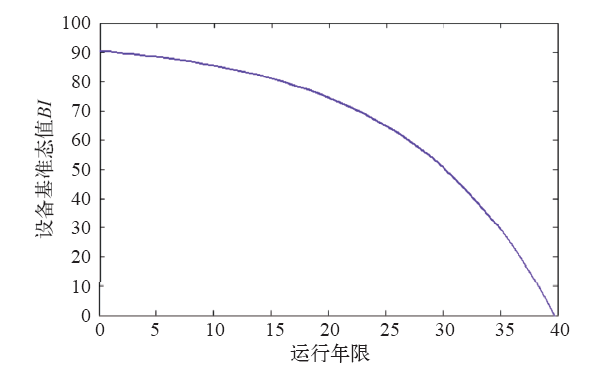
设备基准态轨迹如图4所示。
图4
表5为该型号断路器两年的设备基准态指标BI分布表,将设备基准态指标BI分为8段,通过现场统计得到设备台数。
表5 设备基准态值分布表
Tab.5
| 分类 | 基准态 | 设备数/台 | |
|---|---|---|---|
| 第一年 | 第二年 | ||
| 1 | 95〜100 | 64 | 62 |
| 2 | 85〜95 | 44 | 43 |
| 3 | 75〜85 | 18 | 19 |
| 4 | 60〜75 | 8 | 9 |
| 5 | 45〜60 | 7 | 8 |
| 6 | 30〜45 | 5 | 4 |
| 7 | 15〜30 | 3 | 4 |
| 8 | 15以下 | 0 | 0 |
| 设备总数/台 | 149 | 149 | |
| 故障设备数/台 | 2 | 3 | |
则依据式(7)所述,利用两年的统计数据,通过最小二乘法,计算得设备故障率模型中的比例系数和曲率系数,见表6。
最终得到设备故障率模型为
接着,利用4.2小节中的结论,将式(12)和式(13)代入式(11),最终得到设备的可靠性模型为
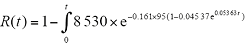
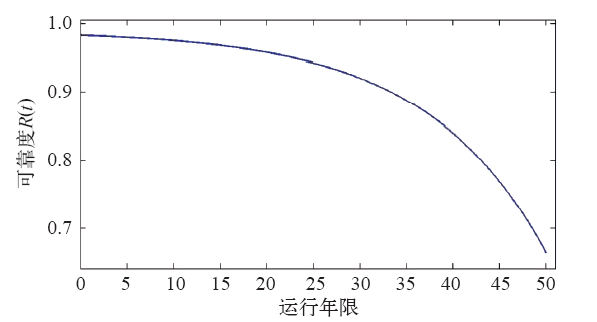
由上式得出的设备可靠性曲线如图5所示。
图5
由图5可以看出,设备的可靠性随着运行时间的增加呈下降趋势,在投运前期可靠性相对稳定,下降趋势平缓;到达后期设备可靠性下降速度会加快。
6 结论
本文基于基准态的概念,提出了一种利用电网强度、设备强度及设备老化程度综合评价高压断路器运行状态的方法。作为基准态分析的延续,利用数理统计的结论,构建了基准态预测模型,预测设备基准态发展趋势。最后,利用文章提出的故障率模型及可靠性模型,计算及预测设备当前或未来的可靠度指标,为用户的运维及检修工作提供决策支持。
参考文献
输变电设备智能化运维系统研究与应用
[J].
Study on power transmission and transformation equipment intelligent operation and maintenance system and its application
[J].
展望“十二五”电力发展战略
[J].
Outlook "Twelve five" power development strategy
[J].
输变电设备故障率的估算方法
[J].
Estimation method for the failure rate of transmission and transformation equipments
[J].
状态检修决策中的电气设备故障率推算
[J].
Prediction of electrical equipment failure rate for condition-based maintenance decision-making
[J].
输变电设备状态故障率模型改进分析
[J].提出了以设备健康状态模型为基础,模型参数随时间变化的输变电设备故障率模型改进方案。还为改进模型的参数求解提出了新方法———全状态集成法。全状态集成法是对设备带有时间标签的完整健康过程进行研究,跟踪利用全过程的状态信息,因此得到的模型参数都带有役龄标记。最后通过实例,运用全状态集成法计算了改进模型中不同役龄设备的模型参数值和故障率,与原模型及反演法计算的结果相比,更接近实际统计到的故障率数值。
Improvement of state failure rate model for power transmission and transforming equipment
[J].提出了以设备健康状态模型为基础,模型参数随时间变化的输变电设备故障率模型改进方案。还为改进模型的参数求解提出了新方法———全状态集成法。全状态集成法是对设备带有时间标签的完整健康过程进行研究,跟踪利用全过程的状态信息,因此得到的模型参数都带有役龄标记。最后通过实例,运用全状态集成法计算了改进模型中不同役龄设备的模型参数值和故障率,与原模型及反演法计算的结果相比,更接近实际统计到的故障率数值。