1 引言
国内外对电弧诊断的研究大致包括:①建立电弧模型,通过模型参数研究故障电弧,目前主要停留在仿真分析阶段。②根据电弧发生时所产生的物理现象,如弧声、弧光、辐射及温度变化等物理量检测电弧。③根据线路电流和电压波形检测电弧。
文献[3]从故障电弧产生的声、光、磁等物理现象角度对故障电弧的检测方法进行了研究。但由于故障电弧的不确定和多样性,故障电弧所表现的特征也并非单一固定不变,基于检测固定位置的声、光、辐射等信号和研究电弧模型等方法存在较大的局限性,因此根据线路电流和电压波形检测电弧是比较好的选择。
文献[4,5]根据电弧电流波形畸变,选取了电弧电流的平均值或者峰值作为特征值进行比较;文献[6]以燃弧前后电流信号为研究对象,提出了基于差值–均方根法的故障电弧检测方法。文献[7]中,TI公司将三周期法(Three Cycle Algorithm,TCA)引入电弧检测,该算法可以强烈凸显电弧引起的电流突变。文献[8,9]发现发生故障电弧时,电流的高次谐波含有率急剧上升。文献[10]将小波分解后的各层信号能量的平均值和标准差作为识别故障电弧的有用信息。文献[11]将小波变换后各频段细节信号的模极大值作为特征向量,利用神经网络构建特征向量与电弧故障之间的映射关系进行电弧故障诊断。虽然串联型故障电弧的研究工作取得了一些研究成果,但目前已有的电弧时域特征的研究主要集中在电流峰值、有效值和斜率等方面,这些特征值虽然计算量小,却容易受到负载类型和电流大小变化等因素的影响。神经网络等方法需要对大量样本进行训练,计算量相对较大。而频域方法在故障电弧在线检测方面取得了较好的效果[12]。
本文通过开展不同类型负载线路的航空交流系统串联型故障电弧模拟试验,利用小波包技术和信息熵理论选择最优的小波母函数和分解层数对发生故障电弧前后的电流信号进行特征频段的提取。进而,比较特征频段下故障电弧发生前后电流信号的间谐波特征。结果表明该方法使得电弧发生前后间谐波特征量的差值提高了2倍,更容易将故障电弧电流与正常电流区分开。
2 试验
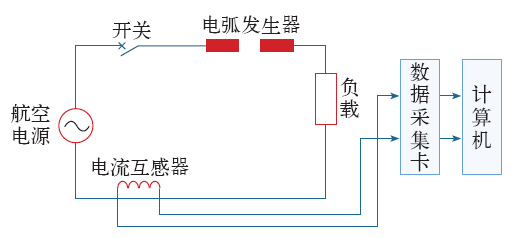
参照标准[13]搭建了串联型故障电弧试验平台,模拟航空交流系统串联型故障电弧的发生。
图1
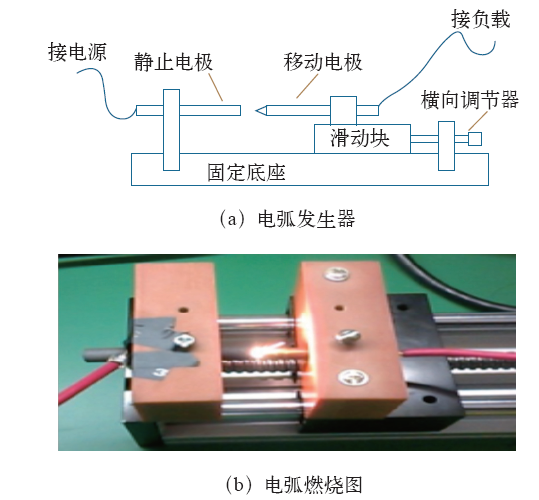
图2
试验中电源电压为交流115V/400Hz;数据采集卡的采样频率fs设置为400kHz。
为了增强电弧检测方法的普适性,本文分别选取了纯组性、阻容性和阻感性负载进行故障电弧模拟试验,将试验方案及负载统计于表1。
表1 试验电路负载统计
Tab.1
| 序号 | 负载类型 | 正常周期数/组 | 故障周期数/组 | 组数 |
|---|---|---|---|---|
| 1 | 230Ω | 10 | 10 | 10 |
| 2 | 230Ω+4.7μF | 10 | 10 | 10 |
| 3 | 230Ω+10mH | 10 | 10 | 10 |
本文以5个周期作为一个信号分析单元。每组数据中截取故障电弧发生前后各10个周期的电流信号。这样,每组数据各含有2个正常信号分析单元、2个故障信号分析单元。每种负载共包含10组数据,40个信号分析单元。整理好的数据留以备用。
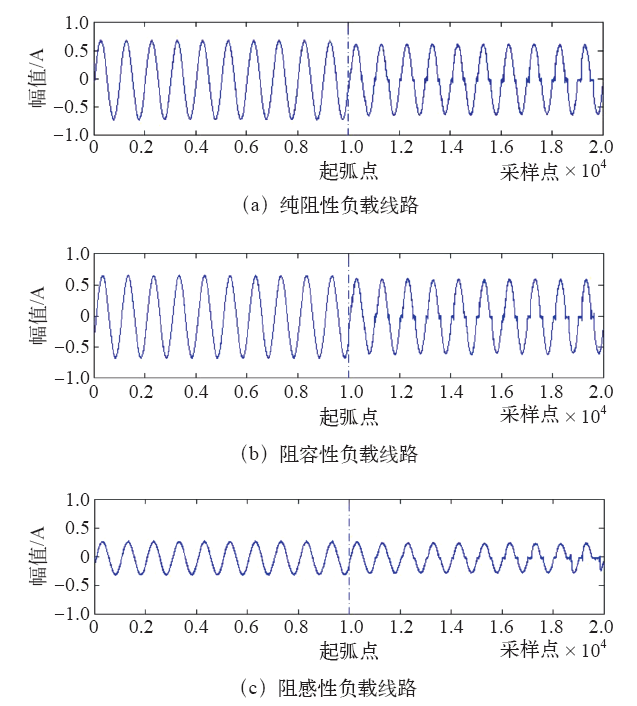
分别从3种负载线路的10组试验数据中随机地选择一组数据,其波形如图3所示。
图3
图3
不同负载线路故障电弧发生前后电流波形图
Fig.3
The current waveforms before and after the arcing of different experimental loads
3 特征频段的提取
3.1 小波包理论
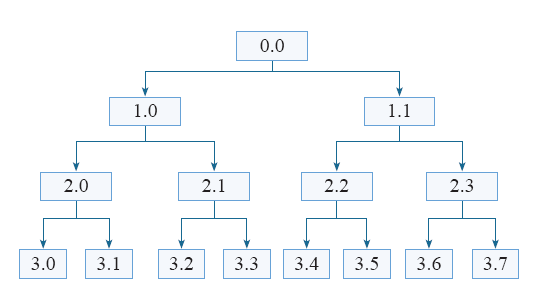
图4
其中,节点(0,0)为原信号。节点(m,n)表示信号经m层小波包分解得到的第n + 1个子频段。三层小波包分解结构中各节点系数与各个子频段的对应关系见表2。
表2 三层小波包分解节点与子频段对应关系表
Tab.2
| 节点 | 子频段 | 节点 | 子频段 |
|---|---|---|---|
| (0,0) | [0, fs/2] | (3,1) | [fs/24, 2fs/24] |
| (1,0) | [0, fs/22] | (3,2) | [2fs/24, 3fs/24] |
| (1,1) | [fs/22, fs/2] | (3,3) | [3fs/24, 4fs/24] |
| (2,0) | [0, fs/23] | (3,4) | [4fs/24, 5fs/24] |
| (2,1) | [fs/23, 2fs/23] | (3,5) | [5fs/24, 6fs/24] |
| (2,2) | [2fs/23, 3fs/23] | (3,6) | [6fs/24, 7fs/24] |
| (2,3) | [3fs/23, 4fs/23] | (3,7) | [7fs/24, 8fs/24] |
| (3,0) | [0, fs/24] |
表中节点(m,n)对应子频段[nfs/2(m+1),(n+1)fs/2(m+1)]。由此可见,小波包技术实现了对信号的精细分解,而且这种分解既无冗余,也无遗漏。信号经小波包分解后形成小波包基库,此基库由许多不同正交小波包基组成。不同的小波包基包含不同的频带,能够反映信号在相应频段上的特征。
3.2 参数选择
小波母函数和分解层数共同决定了小波包分解效果的好坏,进而影响了对故障电弧特征频段的提取。因此本文将小波母函数和不同分解层数结合起来对故障信号进行处理,然后分析处理后的结果得出最优母函数和最佳分解层数。3.2.1 小波母函数的选择一般来说,选择小波母函数主要考虑的特性有正交性、紧支性、对称性和消失矩。(1)正交性。由多尺度分解得到的各子频带数据分别落在相互正交的子空间中,使各子频带数据相关性减小。但是能准确重建的、正交的、线性相位和有限冲击响应滤波器组是不存在的,此时一般放宽正交性条件为双正交。(2)紧支性。紧支性是小波的重要性质之一,若函数Ψ(t)在区间[a,b]外恒为零,则称[a,b]为Ψ的支撑,[a,b]的长度为Ψ的支撑长度,[a,b]越小,支撑越小,其局部化能力越强,定位精度越高。(3)对称性。小波母函数的对称性直接影响信号的重构。如果具有对称性,则在重构算法中,就能避免失真,给出原始信号的一个很好逼近。(4)消失矩。小波函数应满足
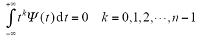
式中,Ψ(t)有n个连续的零点,则Ψ(t)的消失矩为k。消失矩的大小决定了用小波逼近光滑函数的收敛率。当k = 0时,表明Ψ(t)是一个迅速衰减且平均值为0的波。为了可以有效地检测出奇异点,分析突变信号时所选的小波母函数必须具有足够高的消失矩。然而,Daubechies已经证明,除了haar小波基,不存在对称的紧支正交小波基。而对于双正交小波基,可以合成具有对称或反对称的紧支小波基。因此,对于具有双正交性的母函数,其对称性对小波包分解结果的影响程度就减小了。现将常用的小波母函数类型和性质列入表3中。
表3 常见小波母函数及性质表
Tab.3
| 类别 | 双正交 | 紧支 | 对称 | 消失矩 |
|---|---|---|---|---|
| haar | 有 | 有 | 对称 | 1 |
| dbN | 有 | 有 | 近似对称 | N |
| biorNr.Nd | 有 | 有 | 不对称 | Nr - 1 |
| coifN | 有 | 有 | 近似对称 | 2N |
| symN | 有 | 有 | 近似对称 | N |
| meyr | 有 | 无 | 对称 | — |
通过观察表3中几个常用小波母函数及性质可知,haar、meyr这两种母函数的消失矩不存在或太小,biorNr.Nd小波不具有对称性,都不适合用于本文对特征频段提取的研究;因此,本文将从coifN(N = 1,2,…,5)、symN(N = 2,3,…,8)、dbN(N = 1,2,…,10)小波中选取最优的母函数,用以小波包分解。
3.2.2 分解层数的选择
考虑到对信号进行划分时,若划分的子频带数量过少,实现不了对频段的细致划分,使特征差异不明显;若划分的子带数量过多,则容易造成特征差异不稳定,同时会增加计算量和特征的冗余量。因此,在对信号进行小波包分解时,需要合理地选择小波包分解层数。如果对信号进行Level层小波包分解,那么频率分辨率df = fs/2(level+1),这里采样频率fs为400kHz,当分解层数Level取17时,频率分辨率df = 400kHz/218 = 1.53Hz。因此,要选用的分解层数Level≤17。
3.2.3 小波奇异熵
需要寻找一个在整体上衡量故障信号不确定性程度的指标。当该指标达到最大时,所采用的小波母函数和分解层数就是最优组合。本文选用的指标为小波奇异熵(Wavelet Singularity Entropy,WSE)增量。设信号s经m层小波分解的结果为一个m×n的矩阵Dm×n,根据信号奇异值分解理论,对于一个m×n的矩阵D,必然存在一个m×l维的矩阵U和一个l×n维的矩阵V,和一个l×l维的矩阵Λ,使得矩阵D分解为
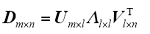
式中,对角矩阵Λ的主对角线元素λi(i = 1,2,…,l)是矩阵Dm×n的奇异值。则WSE定义为
式中,pi为第i阶小波奇异熵。
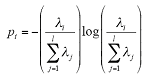
对小波分解结果矩阵进行奇异值分解相当于将彼此存在关联的小波空间映射到线性无关的特征空间。小波空间的奇异熵,在综合冗余信息的基础上,直接反映了被分析信号时–频空间中特征模式能量的分布不确定性。不同的小波母函数和分解层数组合,会得到不同的小波奇异熵值。当选用的小波母函数和分解层数组合为最优组合时,小波奇异熵值增量达到最大。因此,小波奇异熵的增量可以作为衡量故障信号复杂性或不确定性程度的指标。
分别从3种负载线路的10组试验数据中随机地选择1个故障电弧电流的分析单元。对这3个故障电弧信号进行归一化处理。然后分别采用不同的小波母函数和分解层数组合,按照式(3)和式(4)计算小波奇异熵值。最后计算采用不同小波母函数时,小波奇异熵增量随分解层数增加的变化情况。其中,小波母函数对应序列号见表4。
表4 小波母函数排序表
Tab.4
| 小 波 | 序 号 | 小 波 | 序 号 | |
|---|---|---|---|---|
| db1 | 1 | sym3 | 12 | |
| db2 | 2 | sym4 | 13 | |
| db3 | 3 | sym5 | 14 | |
| db4 | 4 | sym6 | 15 | |
| db5 | 5 | sym7 | 16 | |
| db6 | 6 | sym8 | 17 | |
| db7 | 7 | coif1 | 18 | |
| db8 | 8 | coif2 | 19 | |
| db9 | 9 | coif3 | 20 | |
| db10 | 10 | coif4 | 21 | |
| sym2 | 11 | coif5 | 22 |
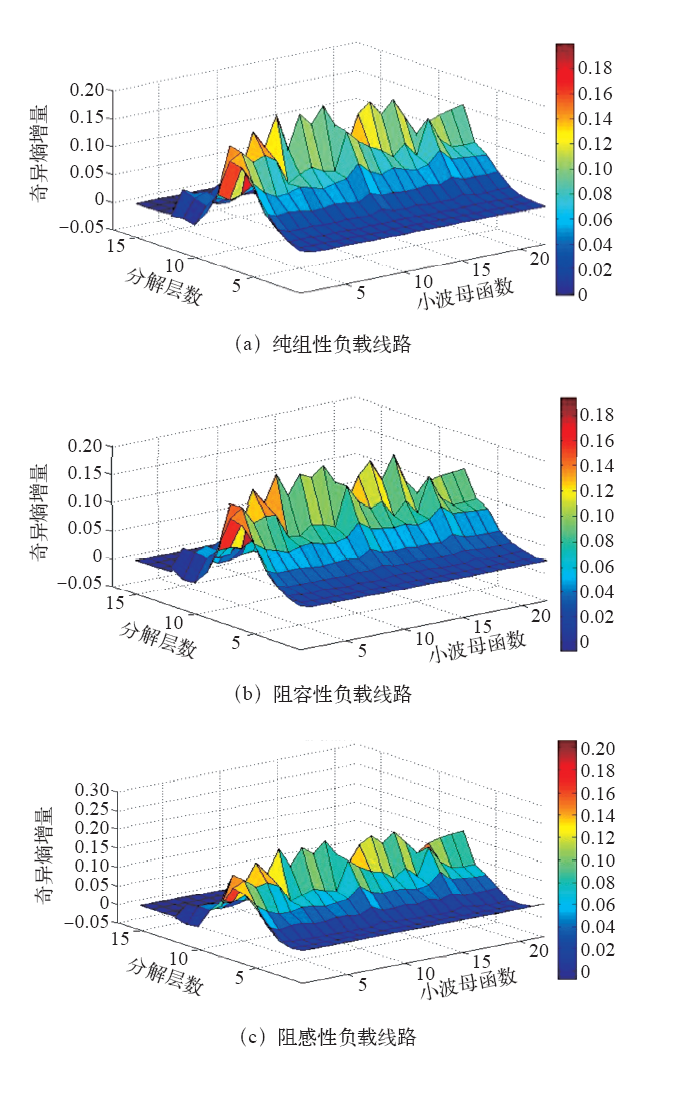
为了直观地观察不同参数组合的效果,将所得小波奇异熵增量数据绘制成带填充色的二维等高线,如图5所示。
图5
图5
小波母函数和分解层数对电弧电流奇异熵增量的影响
Fig.5
The effect of mother wavelet and decomposition levels on the increment of the arc current singular entropy
图6
图6
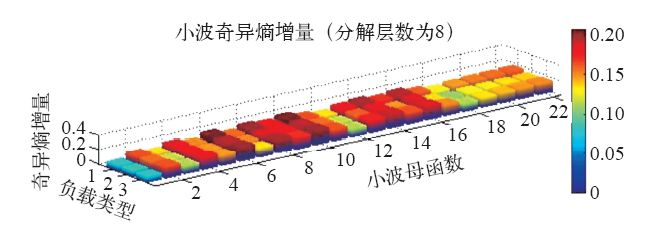
小波母函数对电弧电流奇异熵增量的影响
Fig.6
The effect of mother wavelet on the increment of the arc current singular entropy
综上,当小波母函数选db6、db8、db10、sym5或sym7,分解层数为8时,通过小波包技术提取故障电弧电流信号的特征频段最准确。
3.3 提取特征频段
通过试验得到了3种负载线路的电流信号数据各10组,每组包含2个正常电流信号分析单元和2个电弧电流信号分析单元,即每种负载都对应有20个正常电流的信号分析单元和20个电弧电流的信号分析单元。3种负载共有60个正常电流的信号分析单元和60个电弧电流的信号分析单元。
首先,分别对每个信号分析单元采用db6、db8、db10、sym5、sym7小波进行8层小波包分解与重构,并对重构后的信号进行归一化处理;然后再根据式(5)计算信号经归一化后的信息熵;最后,计算故障电流信号分析单元与正常电流单位分析信息熵的比值。根据信息熵的负熵理论,熵值减小量越大,则系统包含的信息量越大,对于重构后的故障电弧电流信号来说,某一频段故障电弧电流信号与正常电流信号相比信息熵值的减小量越大,那么此频段存在的故障电弧的影响因素也就越多,也就是故障电弧发生时的特征频段。
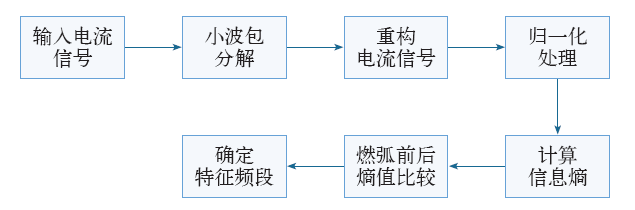
利用信息熵理论提取故障电弧的特征频段。特征频段的提取过程如图7所示。
图7
图7
特征频段提取过程示意图
Fig.7
The schematic diagram of feature frequency extraction process
小波包分解和重构实现了对原始信号的频域抽取;不同负载电流幅值不同,同一负载在不同时刻电流幅值也不同。因此,对重构后的电流信号进行归一化处理。使电流信号各子频段的特征量具有可比性。信息熵为
式中,n为采样点数;x(ti)为电流信号的时间序列。
根据式(5)计算,得到采用4种不同小波母函数时,每种小波母函数对应有60个正常电流的信息熵和60个电弧电流信息熵。对来自同一组数据的信号分析单元计算故障电流信号分析单元与正常电流分析单元的信息熵比值。并计算每种小波母函数对应的60个信息熵比值的平均值。本文对信号进行了8层小波包分解,共得到28个频段的信息,子频段带宽dw = fs/(29) = 781.25Hz。信息熵比值平均值较小的前10个值见表5。
表5 信息熵比值平均值
Tab.5
| 序号 | db6 | 子频段 | db8 | 子频段 | db10 | 子频段 | sym5 | 子频段 | sym7 | 子频段 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 1 | 1.0 | 1 | 0.9 | 1 | 0.9 | 1 | 1.0 | 1 |
| 2 | 1.1 | 69 | 1.1 | 77 | 1.1 | 69 | 1.1 | 2 | 1.2 | 77 |
| 3 | 1.4 | 205 | 1.5 | 197 | 1.5 | 205 | 1.3 | 69 | 1.5 | 69 |
| 4 | 1.5 | 77 | 1.5 | 69 | 1.6 | 77 | 1.3 | 77 | 1.5 | 197 |
| 5 | 2.0 | 2 | 1.8 | 205 | 1.8 | 197 | 1.5 | 205 | 1.8 | 205 |
| 6 | 2.1 | 197 | 3.6 | 2 | 4.4 | 206 | 1.6 | 197 | 2.7 | 2 |
| 7 | 4.3 | 17 | 4.2 | 78 | 4.5 | 208 | 3.8 | 109 | 3.6 | 206 |
| 8 | 4.3 | 75 | 4.6 | 203 | 4.6 | 79 | 4.3 | 110 | 4.3 | 75 |
| 9 | 4.4 | 80 | 4.7 | 210 | 4.7 | 198 | 4.4 | 223 | 4.5 | 49 |
| 10 | 4.5 | 223 | 4.8 | 204 | 4.8 | 207 | 4.5 | 49 | 4.7 | 78 |
4 谐波特征
表6 间谐波均值的差值对比
Tab.6
| 信号类型 | 纯阻性 | 阻容性 | 阻感性 |
|---|---|---|---|
| S1 | 10.2 | 9.1 | 8.3 |
| S2 | 5.1 | 3.4 | 3.0 |
| Ratio | 2.0 | 2.7 | 2.8 |
观察表6数据可知,S1信号计算得到的差值大于S2信号计算得到的差值。当线路负载分别为纯阻性、阻容性和阻感性时,S1信号计算得到的差值与S2信号计算得到的差值的比值Ratio分别为2.0、2.7、2.8。因此,先提取特征频段上的信号,然后再计算间谐波均值特征向量到参考点的距离比没有经过特征频段的提取直接进行计算得到的结果更容易将故障电弧电流与正常电流区分开。
5 结论
本文通过对电弧电流和正常电流的研究,得到以下3个结论:
(1)当小波母函数采用sym5,分解层数取为8层时,故障电弧特征频段的提取结果最好。
(2)航空交流系统串联型故障电弧电流信号的特征频段为0~1 562.5Hz;特征频段上的间谐波特征可以作为故障电弧识别的依据。
(3)先提取信号特征频段上的信号,然后再计算间谐波均值比没有经过特征频段的提取直接进行间谐波均值计算的得到结果更容易将故障电弧电流与正常电流区分开。
参考文献
More about arc-fault circuit interrupters
[C].
Arc fault detection and discrimination methods
[C].
Design of arc flash protection system using solid state switch, photo detection, with parallel impedance
[C].
基于差值-均方根法的故障电弧检测的研究
[J].
Research on arc-fault detection based on difference-root mean square method
[J].
低压串联故障电弧电流高次谐波含有率试验
[J].
Experiment on current high order harmonic ratio for series low voltage arc fault
[J].
低压串联故障电弧的识别方法
[J].
Identification method of low voltage series arc fault
[J].
一种基于小波变换能量与神经网络结合的串联型故障电弧辨识方法
[J].针对交流串联型故障电弧发生时回路电流幅值较小、传统线路保护装置不能有效检测的问题,提出一种基于小波变换能量与神经网络结合且适用于多种典型负载的串联型低压交流故障电弧辨识方法。利用自制的电弧发生装置模拟产生低压交流故障电弧,获取了6种典型家用负载情况下电路正常运行及产生串联型故障电弧时回路的电流信号。对采集的信号进行小波分解,将各层细节信号能量的平均值和标准差输入BP神经网络后构成小波神经网络,实现对不同负载测试样本的辨识。采用粒子群优化算法计算神经网络训练初始值,利用自适应学习率方法提高了训练速度。算法输出结果含义明确,输入层特征量选取合理。实验结果表明,采用该方法进行故障电弧辨识的准确率达到95%以上。
Series arc fault identification method based on energy produced by wavelet transformation and neural network
[J].针对交流串联型故障电弧发生时回路电流幅值较小、传统线路保护装置不能有效检测的问题,提出一种基于小波变换能量与神经网络结合且适用于多种典型负载的串联型低压交流故障电弧辨识方法。利用自制的电弧发生装置模拟产生低压交流故障电弧,获取了6种典型家用负载情况下电路正常运行及产生串联型故障电弧时回路的电流信号。对采集的信号进行小波分解,将各层细节信号能量的平均值和标准差输入BP神经网络后构成小波神经网络,实现对不同负载测试样本的辨识。采用粒子群优化算法计算神经网络训练初始值,利用自适应学习率方法提高了训练速度。算法输出结果含义明确,输入层特征量选取合理。实验结果表明,采用该方法进行故障电弧辨识的准确率达到95%以上。
基于小波变换的交流系统串联电弧故障诊断
[J].为实现对用电系统低压用户端中串联电弧故障的准确诊断,根据交流系统中低压串联电弧故障特性,通过自主搭建的电弧故障模拟实验平台及不同负载下的串联电弧故障模拟实验,本文提出一种基于小波变换的串联电弧故障诊断方法。该方法首先采用极大极小原理对信号进行降噪处理,并结合小波变换模极大值对信号进行多分辨分析;将三阶Daubechies小波基函数提取出的各频段细节信号模极大值作为网络输入的特征向量,利用基于阻尼最小二乘法改进的多层前馈(Back Propagation,BP)神经网络构建特征向量与电弧故障之间的映射关系进行故障诊断分类。测试结果表明,该方法可有效实现交流系统中串联电弧故障的诊断分类。
Series arc fault diag-nosis based on wavelet transform in AC system
[J].为实现对用电系统低压用户端中串联电弧故障的准确诊断,根据交流系统中低压串联电弧故障特性,通过自主搭建的电弧故障模拟实验平台及不同负载下的串联电弧故障模拟实验,本文提出一种基于小波变换的串联电弧故障诊断方法。该方法首先采用极大极小原理对信号进行降噪处理,并结合小波变换模极大值对信号进行多分辨分析;将三阶Daubechies小波基函数提取出的各频段细节信号模极大值作为网络输入的特征向量,利用基于阻尼最小二乘法改进的多层前馈(Back Propagation,BP)神经网络构建特征向量与电弧故障之间的映射关系进行故障诊断分类。测试结果表明,该方法可有效实现交流系统中串联电弧故障的诊断分类。
用于交流电弧故障检测的间谐波分析方法
[J].
A method for the detection of AC arc faults by the analysis of interharmonic
[J].
基于小波包能量谱和NPE的模拟电路故障诊断
[J].
Analog circuit fault diagnosis based on wavelet packet energy spectrum and NPE
[J].
Characteristics of series and parallel low current arc faults in the time and frequency domain
[C].