1 引言
二极管钳位型(Neutral Point Clamped,NPC)三电平逆变器由于其输出电压谐波含量小、耐压等级高、开关损耗小等优点,被广泛应用于各种容量的电能变换领域。但三电平逆变器控制目标多,如电流控制、中点平衡控制、共模电压控制等,控制复杂[1]。
有限控制集模型预测控制(Finite Control Set Model Predictive Control,FCS-MPC)根据电力电子系统开关状态有限的特点,构建一个含有多个控制目标的价值函数,然后以价值函数为评判依据,通过在线滚动寻优计算出最佳开关状态[2,3]。由于该方法控制结构简单,动态响应快,可以多目标优化处理,使其在三电平并网逆变器中成为研究热点。但该方法需要给价值函数中每个控制目标分配一个权重系数以代表其重要程度,权重系数越大代表其越重要。其中权重系数的选取对系统控制性能影响很大,且权重系数的整定比较困难[4]。基于FCS-MPC的滞环模型预测控制(Hysteresis Model Predictive Control,HMPC)将滞环控制思想引入到预测控制中,为各控制目标设立不同的控制优先级,通过滚动优化,最终得到最优的开关状态,避免了权重系数的整定过程,同时保留了FCS-MPC动态响应快、多目标优化处理的优点[5]。但FCS-MPC和HMPC系统的开关频率不固定,且开关频率波动范围大,导致逆变器输出电流频谱分布比较分散,不便于系统滤波器的设计。
针对上述问题,为了在改善电流频谱分布的同时,保留MPC多目标优化处理的能力,本文在HMPC基础上提出一种环宽自适应滞环模型预测控制(Adaptive Hysteresis Band Hysteresis Model Predictive Control,AHB-HMPC)方法,将系统的平均开关频率和开关频率波动范围也作为控制目标,引进滞环控制思想,并可在线调整电流滞环大小,实现了系统平均开关频率可控,且开关频率能稳定在以系统平均开关频率为中心的滞环内,使电流的频谱分布集中在系统平均开关频率周围,方便了系统滤波器的设计,同时保留了传统MPC动态响应快、多目标优化处理的优点。
2 HMPC基本原理
2.1 三电平逆变器模型预测数学模型
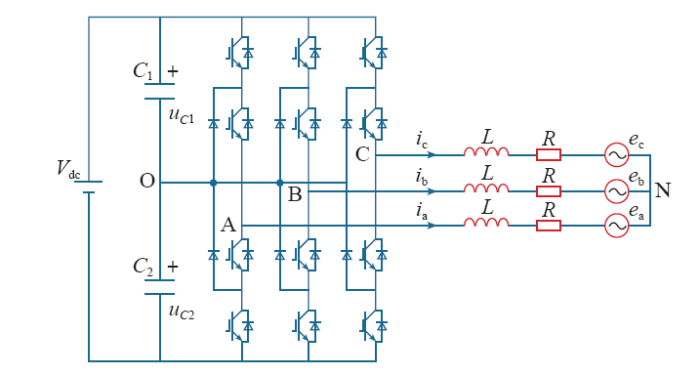
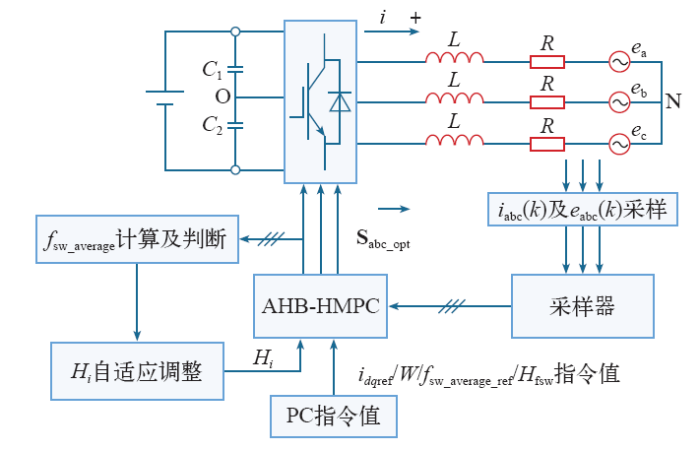
三电平逆变器的拓扑结构如图1所示,其中ea、eb、ec为网侧电网相电压,L为滤波电感,R为寄生电阻,C1、C2为直流侧电容,uC1、uC2分别为C1、C2电压。
图1
在两相同步旋转dq坐标系下,三电平逆变器系统的数学模型为
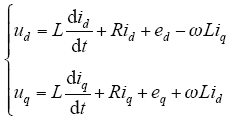
式中,ed、eq为电网电压在d、q坐标系下的分量;ud、uq为逆变器输出电压在d、q坐标系下的分量;id、iq为网侧电流在d、q坐标系下的分量;ω为电网电压角频率。
根据式(1)可得
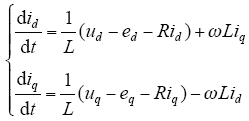
设中点电位u0 = uC1 - uC2,则中点电位数学模型为
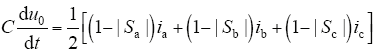
式中,Sj(j = a,b,c)代表各桥臂的开关状态,Sj = 1表示1、2管导通,3、4管关断;Sj = 0表示2、3管导通,1、4管关断;Sj = -1表示1、2管关断,3、4管导通,共有27种开关状态组合。
为了得到系统预测数学模型,对式(1)、式(3)进行离散化处理。将式(1)、式(3)中的微分项进行如下近似处理,即
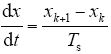
式中,x代表微分变量;xk代表系统第k次采样值;Ts为系统控制周期。
将式(4)代入式(2)可得系统电流预测数学模型为
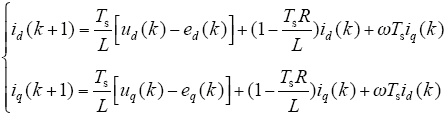
将式(4)代入式(3)可得系统中点电位预测数学模型为
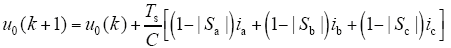
由式(5)、式(6),可根据系统第k次采样值及27种开关状态预测系统第k + 1次网侧电流和中点电位值。
2.2 三电平逆变器HMPC
(1)考虑开关状态硬约束。这部分主要考虑共模电压抑制及保证系统安全。
系统共模电压可表示为
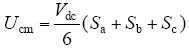
所以,27种开关状态中(1 1 1)、(-1 -1 -1)两种开关状态所产生的共模电压最大,在系统的优化控制中直接排除这两个开关状态,即零矢量只考虑(0 0 0)。
系统安全要求三电平逆变器输出电压不能跳变过大,因为这容易损坏开关器件,即不允许开关状态在1和-1之间切换,只允许在1和0或-1和0之间切换。例如,如果k时刻的开关状态是(1 0 -1),则(-1 x -1)、(1 x 1)、(-1 x 1)几种开关状态在k+1时刻不允许使用(x = 0或1或-1)。考虑系统安全和共模电压抑制后,可选的开关状态标记为备选开关集合Sop1(n),n为27种开关状态对应的编号(n = 1,2,…,27)。
(2)考虑电流跟踪控制。电流控制具有最高控制优先级。电流控制的目标是保证电流在给定的电流环宽Hi内运行。根据k时刻的电流采样值idq(k)及式(5)可以预测k + 1时刻Sop1(n)内每种开关状态作用下对应的电流值idq(n)(k + 1),所有满足式(8)的idq(n)(k + 1)对应的n号开关状态标记为备选开关集合Sop2(n),继续参与后面的控制,非备选开关状态则被排除。即
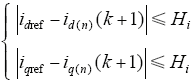
式中,idref为系统有功电流指令值;iqref为系统无功电流指令值。为了使系统工作在单位功率因数条件下,通常取iqref = 0。
(3)考虑中点电位平衡控制。中点电位平衡控制是仅次于电流控制的主控目标。中点电位平衡控制的目标是保证中点电位在给定的中点电位环宽Hu0内运行。根据k时刻的中点电位采样值u0(k)及式(6)可以预测k + 1时刻Sop2(n)内各开关状态作用下对应的中点电位值u0(n)(k + 1),所有满足式(9)的u0(n)(k + 1)对应的开关状态被标记为备选开关集合Sop3(n),参与最后的开关频率抑制,非备选开关状态则被排除。即
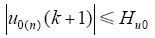
(4)考虑开关频率抑制。开关频率抑制旨在降低系统开关频率,以降低系统开关损耗,提高系统效率。根据式(10),在Sop3(n)中选择具有最小开关切换量Sswitch的开关状态Sjn( j = a,b,c)作为最终的最优开关状态Sabc_opt。即
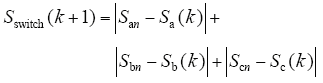
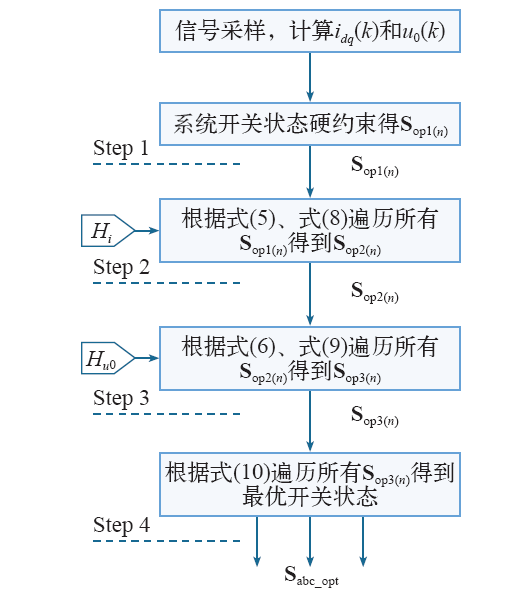
如上所述,三电平逆变器HMPC算法流程框图如图2所示。
图2
3 AHB-HMPC
3.1 三电平逆变器输出电流频谱分析
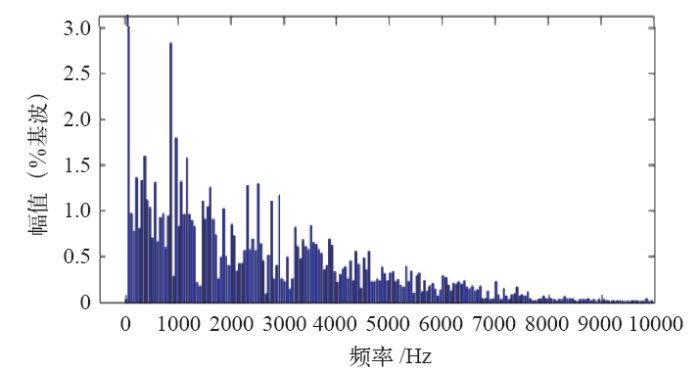
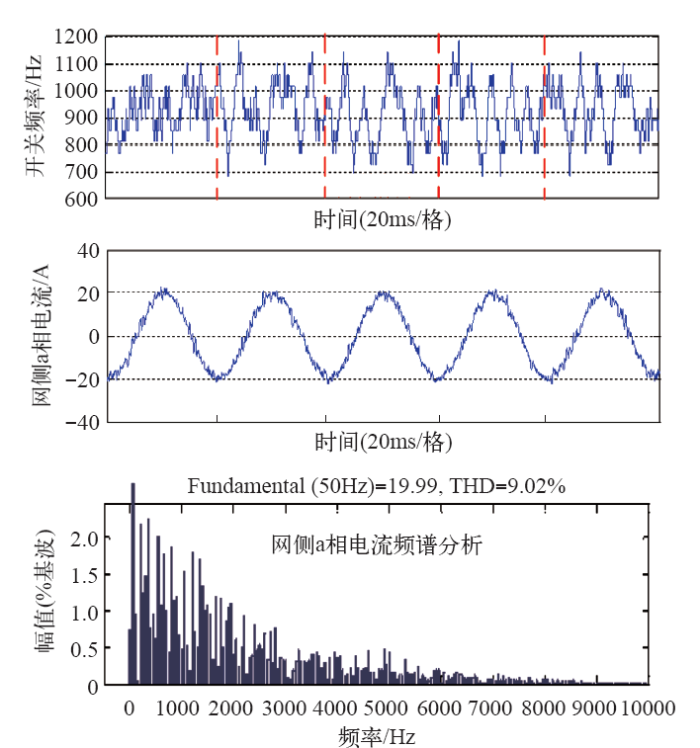
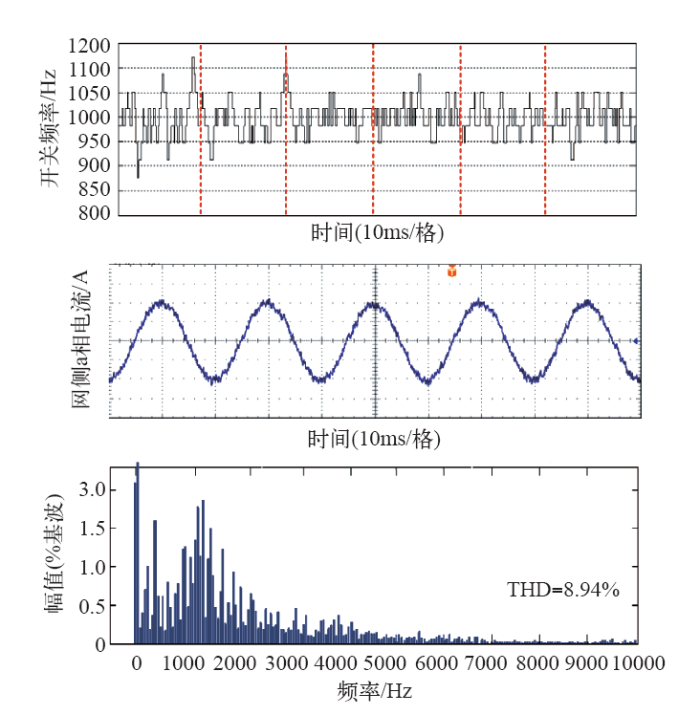
HMPC应用在三电平逆变器中,虽然能够将电流和中点电压控制在所给定的滞环环宽内,但其最后的开关频率抑制旨在降低系统开关频率,以开关状态切换量最小为原则,输出的开关状态没有规律,开关频率波动范围大,最终使得系统输出电流频谱分布分散,给系统滤波器的设计带来困难。HMPC系统输出电流频谱分布如图3所示。
图3
3.2 三电平逆变器AHB-HMPC
AHB-HMPC应用在三电平逆变器上,控制目标包括电流跟踪控制、中点电压平衡控制、共模电压控制、系统平均开关频率大小及开关频率波动范围控制。AHB-HMPC控制流程类似传统HMPC,不同的是AHB-HMPC对开关频率的控制不再一味追求开关状态切换量最小化,而是综合考虑系统的平均开关频率大小和开关频率的波动范围两个指标,其中开关频率的波动范围直接和输出电流频谱分布相关,最终实现开关频率和电流频谱分布的协调控制。
系统平均开关频率大小和系统的开关损耗相关,其值越大,系统开关损耗越大。平均开关频率定义为
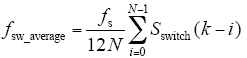
式中,fs为采样频率,N = fs /fi(fi为基波频率)。Sswitch(k - i)可由式(10)计算获得。
系统开关频率波动范围指的是瞬时开关频率相对系统平均开关频率的偏移量,反映的是开关频率的变化率,定义瞬时开关频率为
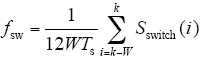
式中,Ts为控制周期;W为瞬时开关频率统计窗口大小,即计算瞬时开关频率大小所用的控制周期数。Sswitch(i)可由式(10)计算获得。
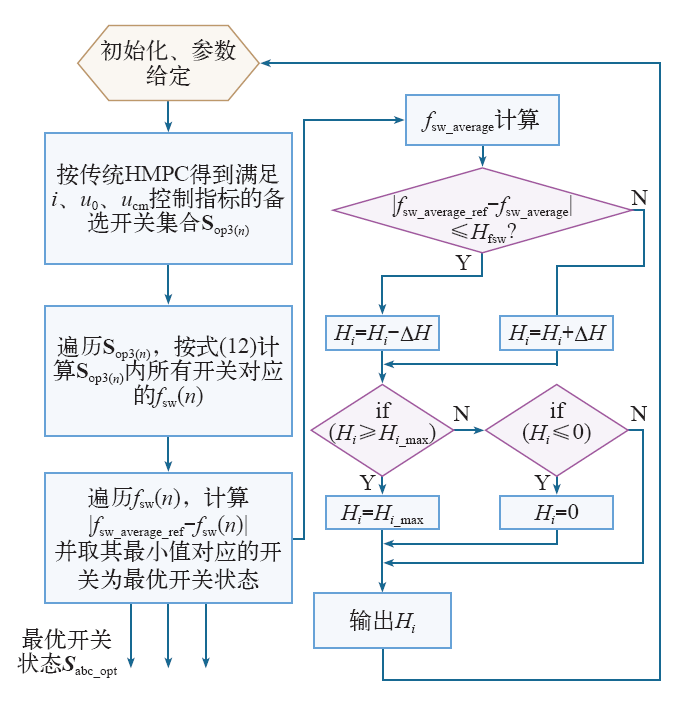
AHB-HMPC算法流程如图4所示。
图4
流程中有两点需要说明:
(1)传统HMPC最后开关频率优化追求的是相邻两个控制周期的开关切换量最小化,以实现开关频率的最小化,而AHB-HMPC在开关频率优化时,选择的标准是选择距离fsw_average_ref(系统平均开关频率指令值)最近的fsw(n)对应的开关状态为最优开关状态,以实现平均开关频率跟踪控制并减小开关频率的波动范围。
(2)传统HMPC中电流的环宽是固定的,导致系统稳态时平均开关频率不可调,且环宽的大小不好整定。AHB-HMPC中电流环宽采用的是自适应策略,以实时增加或减小开关频率控制自由度,同时电流环宽设定只需要根据系统最大纹波电流要求设定一个最大电流环宽Hi_max以及最小值0。控制过程为:首先,设定一个合适的平均开关频率指令值fsw_average_ref以及允许平均开关频率偏离fsw_average_ref的滞环环宽Hfsw;其次,实时按式(11)计算系统平均开关频率fsw_average,当fsw_average在以fsw_average_ref为中心、Hfsw为环宽的滞环内时,认为开关频率处于可控状态,且控制具有冗余自由度,此时以步长∆H为单位逐步减小电流环宽Hi,以减小电流纹波大小;当fsw_average处于滞环之外时,认为开关频率控制缺少自由度,此时以步长∆H为单位逐步增加电流环宽Hi,以增大开关频率控制自由度;最后,判断Hi大小是否处于最大值和最小值之间,否则取最大值或最小值。三电平逆变器AHB-HMPC系统控制框图如图5所示。
图5
图5
三电平逆变器AHB-HMP系统控制框图
Fig.5
Control block diagram of the three-level inverter AHB-HMPC system
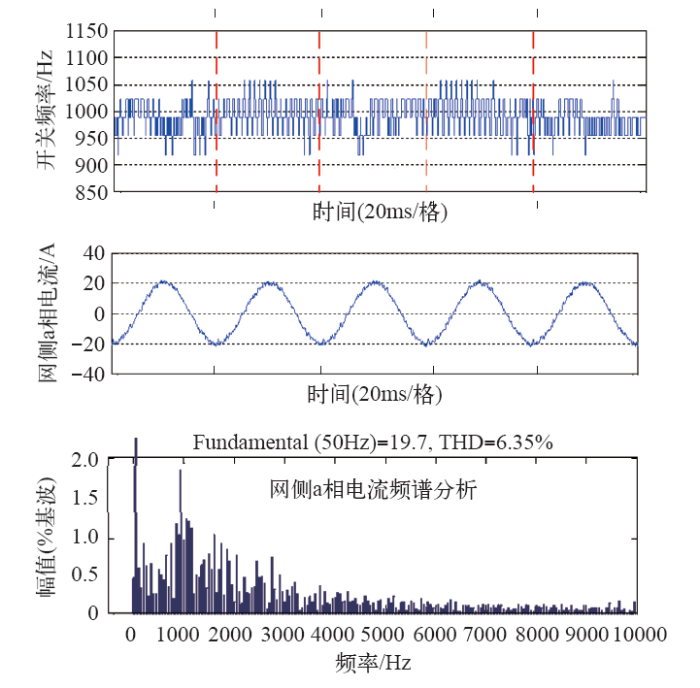
4 仿真验证
图6
图7
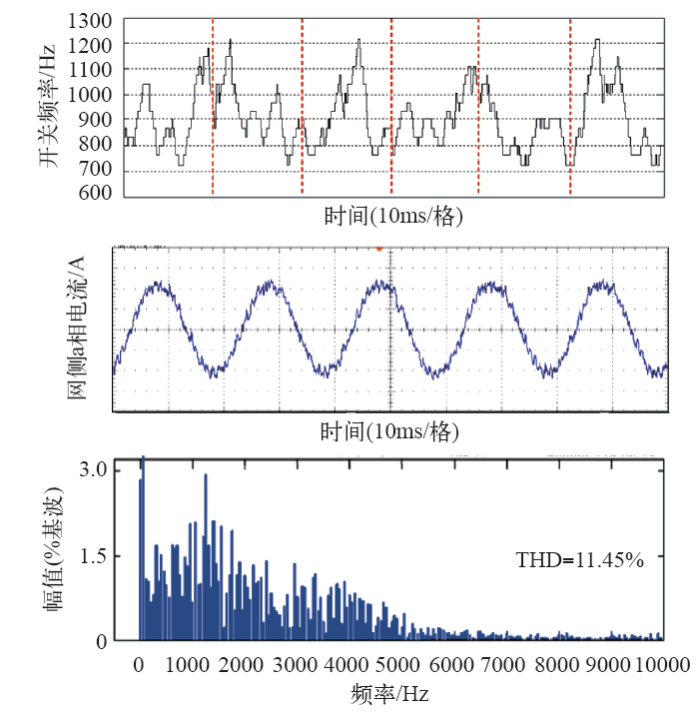
5 实验验证
表1 实验平台参数和实验软件参数(没有1)
Tab.1
| 参 数 | 数 值 |
|---|---|
| 并网相电压峰值/V | 50 |
| 直流侧总电压/V | 200 |
| 网侧滤波电感/mH | 1.5 |
| 直流侧电容C1和C2 /μF | 1 680 |
| 寄生电阻R /Ω | 0.01 |
| 控制周期Ts /μs | 120 |
| fsw_average_ref /Hz | 1 000 |
| 开关频率滞环环宽Hfsw /Hz | 50 |
| 瞬时开关频率统计窗口W | 20 |
| 仿真/实验电流指令值idref/A | 20/10 |
| 最大电流环宽Hi_max /A | 3.5 |
图8
图9
6 结束语
传统HMPC因其控制结构简单、容易实现多目标优化控制而得到广泛关注,但其存在开频率不固定且变化范围大、电流频谱分布比较分散的缺点,导致系统滤波器设计困难。本文在传统HMPC的基础上,将系统平均开关频率大小及开关频率波动范围作为控制目标,并在线调整电流环宽大小,以增加开关频率控制自由度,实现了开关频率的准定频控制,改善了电流频谱分布。仿真和实验结果均证明了所提控制方法的正确性。
参考文献
Predictive current control of a voltage source inverter
[J].
DOI:10.1016/j.isatra.2015.10.007
URL
PMID:26549566
[本文引用: 1]

Due to its fault tolerance, a multiphase brushless direct current (BLDC) motor can meet high reliability demand for application in electric vehicles. The voltage-source inverter (VSI) supplying the motor is subjected to open circuit faults. Therefore, it is necessary to design a fault-tolerant (FT) control algorithm with an embedded fault diagnosis (FD) block. In this paper, finite control set-model predictive control (FCS-MPC) is developed to implement the fault-tolerant control algorithm of a five-phase BLDC motor. The developed control method is fast, simple, and flexible. A FD method based on available information from the control block is proposed; this method is simple, robust to common transients in motor and able to localize multiple open circuit faults. The proposed FD and FT control algorithm are embedded in a five-phase BLDC motor drive. In order to validate the theory presented, simulation and experimental results are conducted on a five-phase two-level VSI supplying a five-phase BLDC motor.
Predictive control of a three-phase neutral-point- clamped inverter
[J].
DOI:10.1016/j.isatra.2017.07.027
URL
PMID:28823416
[本文引用: 1]

This paper presents a new control strategy based on finite-control-set model-predictive control (FCS-MPC) for Neutral-point-clamped (NPC) three-level converters. Containing some advantages like fast dynamic response, easy inclusion of constraints and simple control loop, makes the FCS-MPC method attractive to use as a switching strategy for converters. However, the large amount of required calculations is a problem in the widespread of this method. In this way, to resolve this problem this paper presents a modified method that effectively reduces the computation load compare with conventional FCS-MPC method and at the same time does not affect on control performance. The proposed method can be used for exchanging power between electrical grid and DC resources by providing active and reactive power compensations. Experiments on three-level converter for three Power Factor Correction (PFC), inductive and capacitive compensation modes verify the good and comparable performance. The results have been simulated using MATLAB/SIMULINK software.
Guidelines for weighting factors design inmodel predictive control of power converters and drives
[C].
Hysteresis model predictive control for high-power grid-connected inverters with output LCL filter
[J].DOI:10.1109/TIE.2015.2477060 URL [本文引用: 2]
Predictive current control strategy with imposed load current spectrum
[J].
DOI:10.1109/TIP.2013.2288004
URL
PMID:24196861
[本文引用: 1]

In many signal processing applications, one wishes to acquire images that are sparse in transform domains such as spatial finite differences or wavelets using frequency domain samples. For such applications, overwhelming empirical evidence suggests that superior image reconstruction can be obtained through variable density sampling strategies that concentrate on lower frequencies. The wavelet and Fourier transform domains are not incoherent because low-order wavelets and low-order frequencies are correlated, so compressive sensing theory does not immediately imply sampling strategies and reconstruction guarantees. In this paper, we turn to a more refined notion of coherence-the so-called local coherence-measuring for each sensing vector separately how correlated it is to the sparsity basis. For Fourier measurements and Haar wavelet sparsity, the local coherence can be controlled and bounded explicitly, so for matrices comprised of frequencies sampled from a suitable inverse square power-law density, we can prove the restricted isometry property with near-optimal embedding dimensions. Consequently, the variable-density sampling strategy we provide allows for image reconstructions that are stable to sparsity defects and robust to measurement noise. Our results cover both reconstruction by ℓ1-minimization and total variation minimization. The local coherence framework developed in this paper should be of independent interest, as it implies that for optimal sparse recovery results, it suffices to have bounded average coherence from sensing basis to sparsity basis-as opposed to bounded maximal coherence-as long as the sampling strategy is adapted accordingly.
静止坐标系下基于最优时间序列的电压型PWM 整流器电流预测控制
[J].有限状态预测控制能够实现静止坐标系下电压型PWM整流器的电流控制, 但开关频率及稳态控制精度方面的缺陷限制了其进一步发展。针对这一问题, 提出了基于最优时间序列的电压型PWM整流器电流控制策略。根据电网电压相位信息筛选非零矢量, 基于电流变化特性预测模型得出不同矢量作用下的电流变化特性, 结合电流给定值构建基于α、β 轴电流误差的价值函数, 以单个采样周期内电流误差最小为约束条件确定非零矢量作用时间。实验结果表明, 本文提出的基于最优时间序列的预测控制策略能够有效弥补有限状态预测控制在开关频率及稳态控制精度方面的缺陷, 在保证稳态控制精度的同时, 实现静止坐标系下电流的准确、快速调节。
Stationary frame current regulation of PWM rectifiers based on predictive control
[J].有限状态预测控制能够实现静止坐标系下电压型PWM整流器的电流控制, 但开关频率及稳态控制精度方面的缺陷限制了其进一步发展。针对这一问题, 提出了基于最优时间序列的电压型PWM整流器电流控制策略。根据电网电压相位信息筛选非零矢量, 基于电流变化特性预测模型得出不同矢量作用下的电流变化特性, 结合电流给定值构建基于α、β 轴电流误差的价值函数, 以单个采样周期内电流误差最小为约束条件确定非零矢量作用时间。实验结果表明, 本文提出的基于最优时间序列的预测控制策略能够有效弥补有限状态预测控制在开关频率及稳态控制精度方面的缺陷, 在保证稳态控制精度的同时, 实现静止坐标系下电流的准确、快速调节。
三相PWM整流器模型预测虚拟电压矢量控制
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.18.008
URL
[本文引用: 1]

传统的模型预测控制(model predictive control,MPC)在一个控制周期内仅可输出单一的离散电压矢量,考虑到变流器拓扑可提离散电压矢量的局限性,三相脉宽调制(pulse width modulation,PWM)整流器存在较大的稳态功率脉动。在分析三相PWM整流器离散预测模型的基础上,提出一种模型预测虚拟电压矢量(model predictive virtual voltage vectors,MPV3)控制方法,通过构建6个虚拟的电压矢量代替传统MPC中的8个离散电压矢量,旨在拓展系统的控制集覆盖范围。首先,根据最近三矢量原则确定构建虚拟电压矢量所需的离散电压矢量,接着以功率无差拍跟踪控制为指标在线求取各离散电压矢量作用时间。为了保证虚拟电压矢量的可实现性,构建相应的目标函数进行矢量作用时间的可行性判断和动态修正。最后,为验证所提MPV3方法的可行性和有效性,分别与传统MPC和占空比优化进行仿真和实验的对比分析,并进一步归类总结出各方法的优缺点及适用范围。
Model predictive virtual voltage vector control for three-phase PWM rectifiers
[J].
DOI:10.13334/j.0258-8013.pcsee.2014.18.008
URL
[本文引用: 1]

传统的模型预测控制(model predictive control,MPC)在一个控制周期内仅可输出单一的离散电压矢量,考虑到变流器拓扑可提离散电压矢量的局限性,三相脉宽调制(pulse width modulation,PWM)整流器存在较大的稳态功率脉动。在分析三相PWM整流器离散预测模型的基础上,提出一种模型预测虚拟电压矢量(model predictive virtual voltage vectors,MPV3)控制方法,通过构建6个虚拟的电压矢量代替传统MPC中的8个离散电压矢量,旨在拓展系统的控制集覆盖范围。首先,根据最近三矢量原则确定构建虚拟电压矢量所需的离散电压矢量,接着以功率无差拍跟踪控制为指标在线求取各离散电压矢量作用时间。为了保证虚拟电压矢量的可实现性,构建相应的目标函数进行矢量作用时间的可行性判断和动态修正。最后,为验证所提MPV3方法的可行性和有效性,分别与传统MPC和占空比优化进行仿真和实验的对比分析,并进一步归类总结出各方法的优缺点及适用范围。
基于满意优化的三电平PWM整流器瞬时开关频率抑制方法
[J].DOI:10.13334/j.0258-8013.pcsee.2014.24.009 URL [本文引用: 1]
Instantaneous switching frequency suppression method for three-level PWM rectifier based on satisfactory optimization
[J].DOI:10.13334/j.0258-8013.pcsee.2014.24.009 URL [本文引用: 1]