晶闸管作为高压直流输电、柔性交流输电等大功率电力电子装置的关键器件,其可靠性直接影响到电力系统的安全稳定运行。半导体理论及试验研究表明,晶闸管的电气特性和使用寿命与结温及其变化有很大关系^[1,2]。因此,研究晶闸管结温或整体温度场的瞬态变化,对提高器件应用的可靠性具有非常重要的意义。

目前,对于晶闸管瞬态热分析和建模的方法主要有试验方法和仿真方法。试验方法需要准确测量结温并进行数据分析,然而芯片内部温度直接测量技术的难度太大,通过通态压降、漏电流或转折电压等参数进行间接测量存在操作不便、参数温度敏感系数低等缺陷,不仅测试成本高且准确性受限制^[3]。仿真方法可分为热阻抗网络法、有限元法和有限体积法。热阻抗网络法将晶闸管每层导热物体视为热阻和热容串级连接而成的热阻抗网络模型,简便易用,但准确性依赖于暂态热阻抗曲线描绘的精确度^[4,5,6]。有限元法需要对晶闸管几何结构划分网格,可将与散热器接触的晶闸管安装面设置为等效对流换热系数,亦可将散热器与冷却介质接触面设置为等效对流换热系数,通过设置较小的时间步长才能得到较为准确的瞬态温度场计算结果,对计算机资源要求高且求解速度慢,瞬态温度场计算的工程应用较少。有限体积法需要对晶闸管、散热器和冷却介质划分网格,流–固耦合面的对流换热系数通过流–固耦合计算自动获得,计算结果比有限元法中直接假定某一等效对流换热系数值的方法更符合实际情况,然而为了准确反映边界层的影响,需要选择较小的网格尺寸,导致网格规模庞大,与此同时,流体区域的压力与速度耦合、迭代计算消耗的资源与时间远远超出有限元法,使得瞬态温度场计算的工程应用相当少。

本文根据晶闸管和水冷散热器的几何结构、各层材料的热物理参数,提出了先基于有限体积法进行精细网格的稳态计算,获取水冷散热器内部流道的对流换热系数分布,然后将对流换热系数分布映射到粗糙网格的有限元模型中提取热传导矩阵和热容矩阵,最后对基于Krylov子空间法的降阶模型进行快速瞬态计算。采用该方法及开发的快速计算程序快速得到了晶闸管组件在复杂损耗波形下的瞬态温度场及管芯最高温度变化曲线。

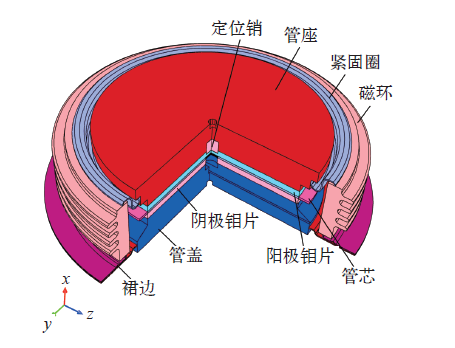
图1为晶闸管的结构示意图,主要由管座、管盖、管芯、阳极钼片、阴极钼片、瓷环等部件组成,这些部件采用的材料名称及热物理参数见下表。管芯产生的热损耗功率通过多层材料的热传导至管座与管盖的外表面,再通过与之接触的水冷散热器中的冷却介质带走。晶闸管组件是包含了晶闸管、水冷散热器、驱动保护模块等部件的集成产品单元,在进行热设计与仿真分析时,需要对晶闸管和水冷散热器这两个最主要的部件进行研究。

采用有限体积法进行晶闸管组件的热仿真时,除考虑各固体材料中的热传导外,还需要考虑流–固耦合面的传热,以及冷却水在水冷散热器内部流道中的流动与换热等。流体流动与换热问题需要满足质量守恒、动量守恒和能量守恒,稳态计算的控制方程可表示成通用形式,即

（1）

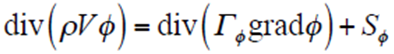
式中,φ、V为通用变量;ρ为密度;Γ_φ为广义扩散系数;S_φ为广义源项。

上述偏微分方程无法直接求解,只能借助诸如有限体积法、有限差分法等数值方法进行计算。有限体积法的基本思路为：首先通过网格划分将计算区域变为一系列不重复的控制体积;然后结合相应的边界条件,将待求解的微分方程对每个控制体积积分,得出一组离散方程;最后通过循环迭代得到计算区域的数值计算结果。有限体积法的典型软件有FLUENT、PHOENICS、Star CCM+、FloTherm等。

在利用FLUENT软件进行稳态计算之前,需要建立晶闸管和水冷散热器的网格模型。考虑到晶闸管内部材料层厚度较小,且水冷散热器内部流道边界层对流动与换热的影响显著,网格尺寸选取0.5mm。仿真对象选取一个晶闸管和两个水冷散热器,利用HyperMesh软件划分出以六面体为主、极少量棱柱体的高质量网格模型,划分后的网格数量为1 018万。

晶闸管工作在正弦电流时的平均损耗功率为

（2）

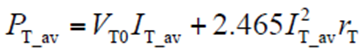
式中,V_T0为导通门槛电压;I_{T_av}为通态平均电流;r_T为通态斜率电阻。

通过电气参数估算出晶闸管芯片在额定工况下的平均损耗功率为6 000W。冷却介质采用40℃去离子水,每个水冷散热器的入口流量为20L/min。冷却水的热物理参数为：密度992.2kg/m³;比热容4 174J/(kg·K);导热系数0.635W/(m·K);动力粘度6.533×10^-4kg/(m·s)。通过手工计算可知水冷散热器入口的Re数为36 160,大于10⁴,可认为是完全湍流,故采用标准k-ε湍流模型进行流动状态的模拟。

利用FLUENT软件针对网格数量多的模型进行流场与温度场计算时,需要不断地迭代计算而消耗大量的计算时间。采用DELL T7600台式工作站进行8处理器并行计算,迭代4 300步消耗时间约为13h后,达到所有残差为10^-6的收敛准则,监控点的温度完全稳定。利用有限体积法进行瞬态计算时,式（1）左边将包含瞬态项,需要对时间积分,计算时间远远大于稳态计算,严重制约了实际工程中的应用,故本文不采用FLUENT软件计算复杂工况的瞬态问题。

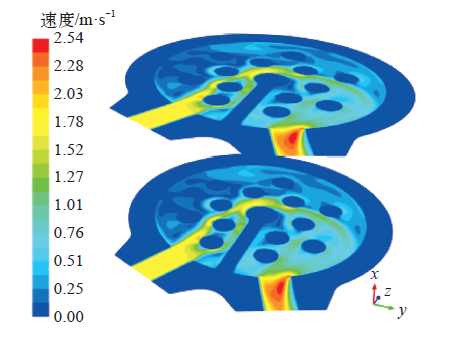
图2为两个水冷散热器中间截面的流速分布,冷却水从入口流入,在流道中受圆柱形翅柱的影响而改变了流动方向。冷却水绕过圆柱形翅柱后,大部分沿着一条流动阻力小的路径流向了出口,出现了水冷散热器内部流速不相等的情况。出口的局部位置流速达到最大值,为2.54m/s。

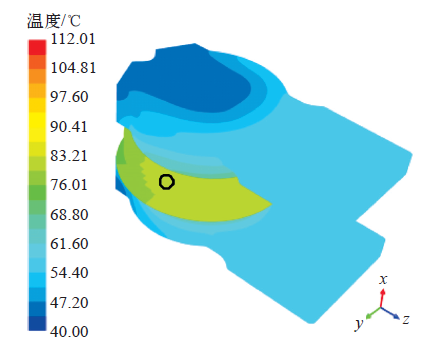
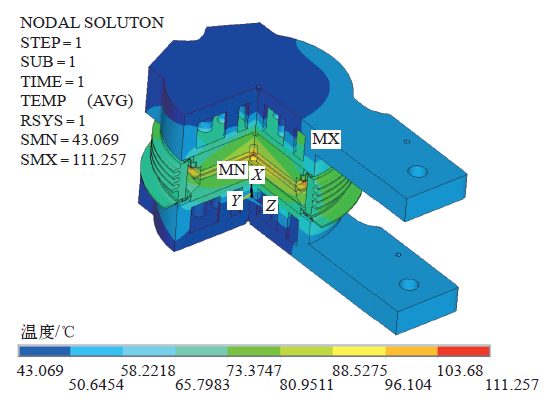
图3所示为晶闸管组件的温度场分布,可以看出晶闸管与两个水冷散热器的外表面温度分布情况,还可从温度标尺看出最高温度为112.01℃,晶闸管磁环上标记点的温度为81.17℃,温升为41.17K。为验证有限体积模型的准确性,对晶闸管组件实物进行了额定工况的温升试验,冷却水温度与环境温度均为30.1℃,测得温度稳定后标记点的温升为39.3K。试验数据低于仿真结果的原因在于仿真模型中未考虑热辐射效应以及热物理参数与实际情况有差异等,然而从温升的相对误差小于5%可知仿真方法是可行的。

牛顿冷却公式引入了对流换热系数（又称表面传热系数）的概念,简化了对流换热的计算,然而对流换热系数的大小与换热过程的许多因素有关,不仅取决于流体的热物理性质以及换热表面的形状、大小与布置,还与流速密切相关。图4为两个水冷散热器内部流道的对流换热系数分布,可以看出不同部位的对流换热系数是有差异的,流速大的部位具有高的对流换热系数,局部的最高对流换热系数可达2.83×10⁴W/(m²·K)。从图4各部位具有不相同的对流换热系数,可以推断将有限元模型流–固耦合面设置为某一定值的对流换热系数,会因边界条件不符合实际情况而存在较大的误差。

利用有限元法计算固体区域的温度场时,瞬态导热问题的微分方程为

（3）

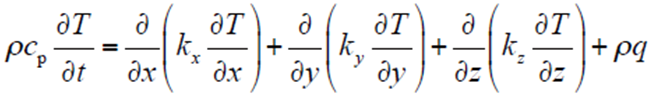
式中,c_p为比热容;T为温度;t为时间;k_x、k_y、k_z分别为x、y和z方向的导热系数;q为物体内部的热源密度。

上述微分方程包含三类边界条件：①规定温度值;②规定热流密度;③规定物体与周围流体间的对流换热系数及周围流体的温度。包含边界条件的微分方程等效积分形式,通过伽辽金提法在空间域有限元离散,可得到n个节点温度T_e（e = 1,2,…,n）的一阶常微分方程组。即

（4）

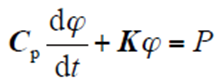
式中,C_p为热容矩阵;K为热传导矩阵;P为温度载荷列阵;φ为节点温度列阵;dφ/dt为节点温度对时间的导数列阵。

在利用有限元法进行稳态计算时,因温度场是标量场,每个节点上只有一个温度未知数,计算较为简单。进行瞬态计算时,不能对n个节点温度的一阶常微分方程组直接求解,需要借助数值求解方法。由于有限元离散使原本具有无限个自由度的问题转变为有限自由度问题,得到的方程具有一定的刚性,对热载荷的响应速度有限,当热载荷变化速度很快时可能出现某些节点上的热量积聚或骤减,从而导致计算结果的数值振荡。为获得稳定解,需要选择较小的时间步长。此外,节点数目n随着模型的复杂程度而增加,矩阵维度会变得非常庞大,因此,求解瞬态温度场问题需要消耗大量的计算资源。

从有限元法的理论基础可知,计算晶闸管组件温度场时,不必对水冷散热器内部的冷却水划分网格与计算,只需在流–固耦合面上施加对流换热系数。其次,有限体积模型选择小尺寸网格的原因主要在于流体边界层效应会对流体区域的流动与换热产生很大的影响,而有限元模型不必考虑流体边界层效应的影响,因此,有限元模型的网格尺寸可以选择大一些。将网格基本尺寸设置为4mm时,利用HyperMesh软件划分出以六面体为主、极少数为棱柱体的有限元网格,如图5所示,并导出有限元网格文件。其中有限元模型的单元数量为46 888,节点数量为50 263。

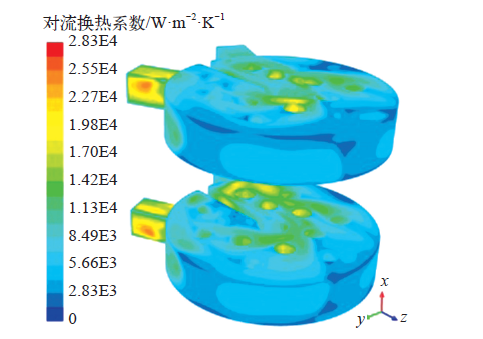
为保证粗糙网格的有限元模型计算结果与精细网格的有限体积模型基本一致,关键在于第三类边界条件的设置需要保持相同。FLUENT软件在载荷映射时提供了整体守恒插值法和图形保留插值法,其中整体守恒插值法可以保证流–固耦合面上总热率平衡,选择该方法可以从精细网格的对流换热系数分布得到粗糙网格的对流换热系数载荷文件。

在ANSYS软件中分别读取有限元网格文件和对流换热系数载荷文件,设置环境温度40℃和管芯损耗6 000W,可在数十秒内计算出稳态温度场结果。为便于查看晶闸管和水冷散热器内部的温度分布情况,隐藏1/4模型后显示出如图6所示的温度场分布,可看出管芯的温度最高,为111.257℃。图6与图3相比,温度场分布基本一致,最高温度值约低0.7%,如此小的误差可说明精细网格的对流换热系数分布向粗糙网格插值处理的有效性,从边界条件的一致性上保证了有限元模型仿真结果的准确性。由于有限元模型的网格数量仅为有限体积模型的4.6%,且不用对耦合的速度与压力迭代求解,使得计算效率提升了700余倍。

在建立的有限元模型基础上,可以利用ANSYS软件提供的HBMAT命令输出热传导矩阵和热容矩阵文件,为深入研究式（4）的快速求解提供数据基础。

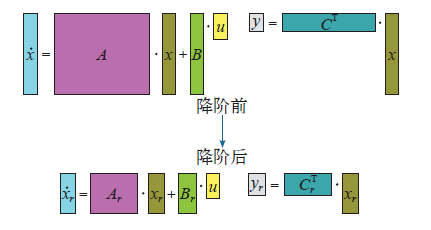
当描述物理场的偏微分方程离散为一组常微分方程时,线性系统的时域问题求解可以转化为状态空间的形式^[7],即

（5）

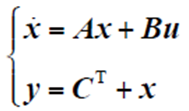
式中,A为n×n矩阵;B、C为n维矢量;u为系统输入;x为状态变量;y为系统输出。

式（5）经拉普拉斯变换后可以得到传递函数G(s),再对传递函数进行泰勒展开。模型降阶的思想是将物理模型的大规模状态空间投影到以一组基矢量为特征的低维空间,借助少量的状态量表示原物理场。基于模型降阶法中最基本和最重要的Krylov子空间法可以确定下式中的A_r、B_r和C_r,建立一个近似原系统的r（rn）维降阶模型^[8,9,10,11]。即

（6）

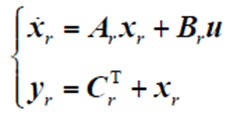
图7为Krylov子空间法进行模型降阶的过程^[7,8],可以较为直观地看出矩阵的维度有大幅度降低,计算模型的复杂度为O(2r²n + 2rN_z(A)),其中N_z(A)为矩阵A的非零单元数。

通过相邻维度降阶模型的传递函数定义相对频率响应误差

（7）

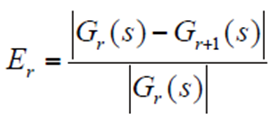
式中,G_r(s)和G_r+1(s)分别为r维和r+1维降阶模型的传递函数。

可以通过程序判断相对频率响应误差小于某一规定值,进而自动获得最小降阶维度,也可通过时间步长选择合适的降阶维度^[10]。Krylov子空间法能很好地解决直接矩匹配方式存在数值不稳定性的问题,计算精度和效率都很高。文献[11]基于ANSYS软件和Krylov子空间法开发了模型降阶计算程序mor4ansys,并应用于微电子和电子产品的瞬态温度快速计算,不足在于未考虑有限元模型中对流换热系数的选取问题,且封装的程序不便于物理场计算结果的提取。许多商业化软件中包含了降阶模型的接口或模块,可实现多个软件的联合仿真,如Simplorer软件向Icepak、Mechanical、Maxwell等软件提供了输出与输入之间建立传递函数关系的模型降阶功能;Comsol软件可以将简化后的模型导出至Matlab/Simulink,作为S函数来调用。这些工具软件为保证计算效率,输出结果是几个探测点的变量变化曲线,很难输出和云图显示整个物理场的数据,不能完全满足实际的应用需求,因此,有必要综合应用有限体积法、有限元法和模型降阶法的优点来解决复杂的实际问题。

为实现瞬态问题的快速准确计算,提出了一种新的方法。首先通过FLUENT模型的稳态计算得到对流换热系数分布,为ANSYS热传导有限元模型提供准确的边界条件;再从ANSYS有限元模型中提取热传导矩阵和热容矩阵文件;然后在Matlab软件中设置热源参数,使用常微分方程求解器对基于Krylov子空间法得到的降阶模型求解;最后将结果投影到原模型上。FLUENT软件的稳态计算和ANSYS有限元模型的矩阵文件提取只需进行一次,Matlab软件中热源设置、降阶模型求解和结果投影等功能与算法可以用m语言开发成快速计算程序,通过循环命令重复执行快速计算程序中的步骤,自动实现热源不断改变条件下的计算^[12]。

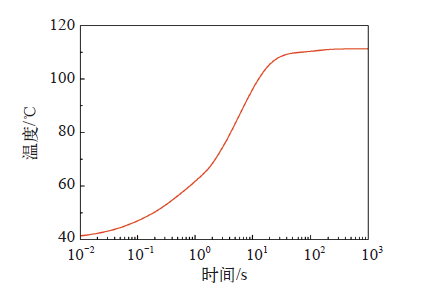
以额定工况的平均损耗功率为输入,利用快速计算程序计算0.01~1 000s时间段的瞬态问题,由于损耗保持不变,降阶阶数可取较小值（如r = 5）^[10],时间步长可取较大值且用对数方式,经过数十秒的计算即可得到有限元模型每个节点在不同时刻的温度结果。在说明瞬态计算结果时,温度场云图只能表示某一时刻不同部位的温度场分布特点,不能表示随时间变化的规律,而曲线可以表示出变量随时间变化的趋势。为便于计算结果的对比,提取了晶闸管组件上的最高温度,绘制而成的温升曲线如图8所示。由图8可知,0.01~20s内的温度迅速上升,之后的温度上升速度变缓,最终完全稳定的温度为111.257℃,该值与ANSYS稳态计算结果完全一致。为考察Matlab软件中模型降阶计算的准确性与效率,利用ANSYS软件计算该工况下的瞬态问题,大约需要23min,快速计算程序计算所得最高温度曲线与ANSYS计算结果完全吻合,可以说明快速计算程序不仅可保证计算结果的准确性,还可使计算效率提升百余倍。

晶闸管组件在众多实际应用中,工况、电气参数、控制策略和负载等是有差异的,导致管芯的损耗会随时间发生变化,属于典型的瞬态问题。流过晶闸管的电流为非正弦波时,根据晶闸管生产厂家提供的通态伏安特性曲线可知通态压降V_T与通态电流I_T的关系

（8）

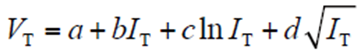
式中,a、b、c、d为通态伏安特性曲线拟合系数。

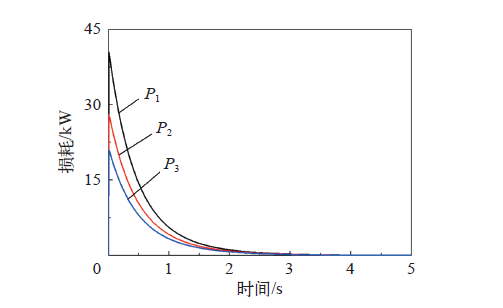
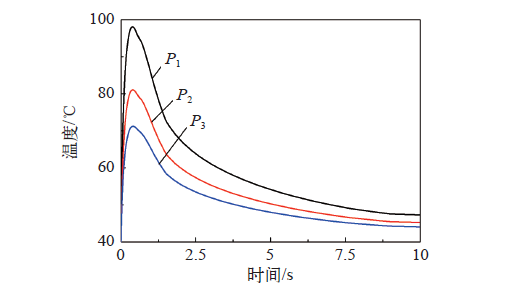
晶闸管的损耗功率可以根据通态压降与通态电流乘积进行计算。晶闸管组件应用于脉冲功率电源时,会在极短的时间快速压缩转换或直接释放电能,电流会突然上升后较为快速的下降。图9为不同的通态电流流过晶闸管时产生的脉冲波形损耗（P₁、P₂和P₃）,损耗从最大值迅速下降至0。由于损耗下降速度很快,需要设置较大的降阶阶数（如r = 30）与较小的时间步长（如Δt = 1ms）^[10],图10是利用快速计算程序得到的三种工况下的最高温度变化曲线,最高温度均表现出先迅速上升再迅速下降,最后缓慢下降的变化趋势。三种损耗中,P₁>P₂>P₃,大的损耗会引起高的温度上升幅度,因此,P₁的温度上升幅度最大,P₃的温度上升幅度最小。

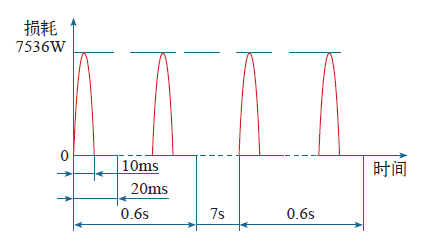
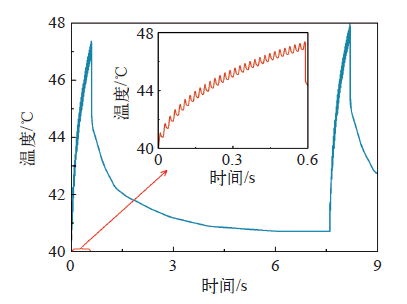
晶闸管采用过零触发方式时,正半周期的正弦波电流流经晶闸管时产生损耗,而负半周期的损耗为0。图11所示为一种半正弦波形损耗的工况：0~0.6s,有30个半正弦损耗波形;0.6~7.6s,没有电流流过,损耗均为0;后续时间里按此规则周而复始。由于一个半正弦波的时间为10ms,需要将半正弦波分成多个时间子步才能体现出波形的特点,因此,时间步长需要选取得相当小（如Δt = 0.2ms）,同时为保证计算的稳定性,降阶阶数需要尽可能大一些（如r = 50）。图12为快速计算程序计算得到的最高温度变化曲线,在0~0.59s,最高温度整体上表现出逐步上升的变化趋势,以20ms为一个周期来看,最高温度则表现出先上升后下降的变化特点;在0.6~7.6s,最高温度下降的特点是先迅速后缓慢;在7.6s时刻,最高温度并未下降至环境温度40℃,因此,新的损耗周期开始时,最高温度是以前一步计算结果为基础叠加。

本文结合晶闸管组件结构及换热机理,讨论了有限体积法与有限元法的特点,提出了一种综合利用有限体积、有限元与模型降阶等方法的优点进行晶闸管组件瞬态温度场快速计算的方法,并开发了快速计算程序,可以在保证边界条件一致性基础上最大程度地提高计算效率来解决多种复杂条件下的瞬态计算问题。该方法可在电力电子器件瞬态温升计算以及疲劳寿命预估分析中推广应用。