1 引言
现如今商用的风电场功率预测系统大都运用组合预测模型,但是由于所有组合预测模型都是在单一预测模型基础上进行的,所以对单一预测模型方法的研究仍是基础和重点。当前在风电功率预测中采用较多的模型有持续模型、物理模型、统计模型和学习模型。在运用学习方法进行短期风电功率预测中,为提高短期风电功率预测精度,人们都将目光放在了对于前期输入数据的处理和对模型本身的优化两方面。目前多采用将统计方法和学习方法结合的功率预测方法,其中前端数据处理用统计方法中的数据挖掘法,后端预测中用各种学习方法。其中比较常见的学习方法有BP神经网络模型和支持向量机(Support Vector Machine,SVM)模型。
在众多学习方法中,SVM法在风电功率预测中对解决小样本、非线性和高维等问题较为有效。但是SVM模型也存在模型参数如何确定的难题。一般来说,SVM模型参数取值没有先验信息,参数选取过于依赖经验判断,存在着一定的随意性,因此需要对SVM模型建立过程中随机生成的参数进行优化。本文采用人工鱼群算法优化SVM模型参数,以建立比较准确的预测模型进行风电功率预测;对于输入数据,本文采用了按天聚类的方法进行处理,最后通过仿真实验验证了该优化算法的可行性。
2 支持向量机
3 聚类分析
聚类分析是一个在数据集中寻找相似元素集合的无监督学习过程[11],是一种多元统计分析方法。聚类分析的基本思想就是把全部需要分类的样本尽可能地分到指定的不同的组中,避免相似的样本分到不同的类中。本文主要运用了K均值聚类与模糊减法聚类两种数据处理方法。运用K均值聚类对数据聚类时需要预先知道数据需要聚类的种数,而本文中NWP数据的分类数不可能预先知道。所以,本文先采用模糊减法聚类来确定其分类数,其特点是对没有先验信息的数据可以确定相应的分类数。
4 人工鱼群算法基本原理
4.1 人工鱼群算法定义
设人工鱼个体状态为X = {xi,i = 1,2,…,n},其中xi为待寻优的控制变量,n为待寻优变量的个数。
设Yi = f(xi)为第i条人工鱼当前所在位置的食物浓度,Yi为目标函数。
设di,j = ||xi - xj||为人工鱼个体之间的距离,人工鱼的感知距离为Visual,人工鱼移动的最大步长为Step,拥挤度为delta,觅食行为尝试最大次数为try_number,当前觅食行为次数为n,最大迭代次数为maxgen。
4.2 人工鱼群算法实现
人工鱼群算法的一般实现步骤为:
(1)初始迭代次数,随机产生初始化人工鱼群。
(2)计算每条人工鱼的食物浓度值,并取最大值。
(3)每条人工鱼按照算法的行为移动,再进行食物浓度值的计算,取最大值,并与步骤(3)的最大值比较,如若优于步骤(2)的最大值,则取而代之。
(4)迭代次数加1并判断是否达到预置迭代次数最大值,如若达到则输出最大值,否则转到步骤(3)。
人工鱼群算法主要包括觅食行为、聚群行为、追尾行为和随机行为。
1)觅食行为。觅食是鱼的基本行为。鱼一旦发现食物会向食物多的地方游去。
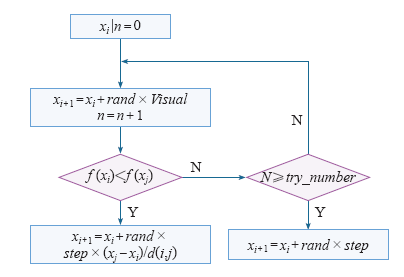
人工鱼个体的当前位置设为xi,在其当前视野范围内(di,j≤Visual)随机选择一个状态xj,当求极大值时,若f(xi)<f(xj),则xi按式(1)向xj移动一步,反之则重新选择状态,观察是否满足前进条件,尝试try_number次后,如若仍不满足条件,则按式(2)随机移动一步。流程如图1所示。
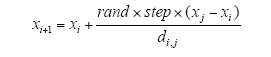
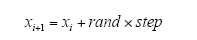
图1
2)聚群行为。聚群行为是鱼类集体觅食和躲避敌害的较常见现象。
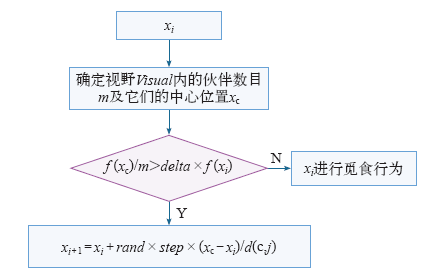
人工鱼个体所处位置为xi,距离其Visual范围内的伙伴数目为m,中心位置为xc,如果f(xc)/m>delta×f(xi),表明中心有较多的食物且不太拥挤,则xi按式(3)向位置xc移动一步,若f(xc)/m<delta×f(xi),则实施觅食行为。同样,如果没看到其他伙伴,也执行觅食行为。聚群行为流程如图2所示。
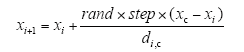
图2
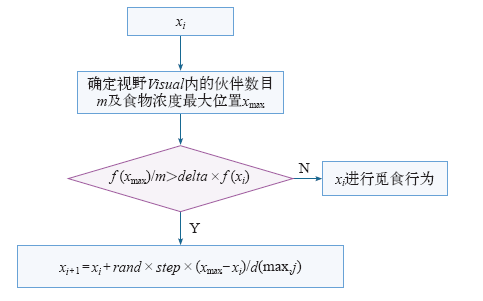
3)追尾行为。人工鱼个体所处位置为xi,距离其Visual范围内所有伙伴中食物浓度值最大的位置为xmax,伙伴数目为m,如果f(xc)/m>delta×f(xi),表明伙伴xj有较多的食物且不太拥挤,则xi按式(4)向位置xmax移动一步,若f(xc)/m<delta×f(xi),则实施觅食行为。同样,如果没看到其他伙伴,也执行觅食行为。
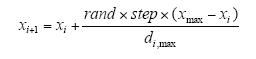
追尾行为流程如图3所示。
图3
4)随机行为。为在更大范围内寻找食物和同伴,鱼类在水中自由游动,人工鱼的随机行为表示为在某一位置内随意朝某一方向移动,即
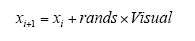
5 基于AFSA-SVM建立模型
5.1 训练数据的选择和归一化处理
风电场所处位置的风速、风向、温度、气压等参数对功率预测的结果都有很大影响。本文以风电场NWP数据中的风速,风向的正弦和余弦值、温度、气压作为支持向量机回归预测的输入数据,以风电场的实测功率作为输出。
为减小某些偏差数据对预测效果的影响,需要采用式(6)的方法,对NWP数据的风速、温度、气压和实际功率等输入、输出数据进行归一化处理。
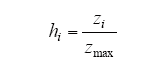
式中,hi为训练样本中某一变量数据zi归一化后的数据;zmax为风电场某一变量数据zi的历史最大值。
5.2 训练数据按天聚类
本文将每天作为一个数据进行处理,用一个7维向量表示为X = [Vmin, Vmax, Dcos, Dsin, Tmax, Tmin, Pav],X中各分量分别表示当天风速最大值、风速最小值、风向正弦平均最大值、风向余弦平均值、气温最大值、气温最小值和气压平均值。本文对这些天的数据运用模糊减法聚类和K均值聚类进行聚类分析。
5.3 AFSA-SVM预测模型的建立
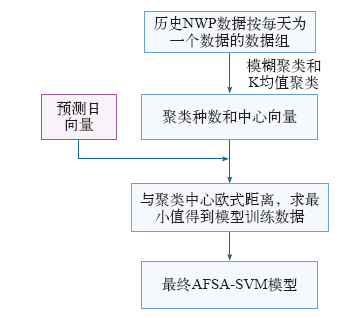
基于AFSA-SVM风电功率预测的流程如图4所示,其中目标函数是平均方均根误差的倒数。
图4
具体建模步骤如下:
(1)首先选取训练样本并进行归一化处理,对训练数据进行按天聚类,得到其分类和聚类中心。运用预测日向量与聚类中心欧氏距离最短判定预测日属于哪一类,取出这类数据作为下面模型的训练数据。
(2)初始化人工鱼群算法和支持向量机回归的各项参数。
(3)以支持向量机回归的平均方均根误差倒数为适应度,根据本文第3.2节中AFSA算法步骤对SVM模型参数进行优化。
(4)利用步骤(2)中优化的模型参数对支持向量回归机模型进行重新训练。
(5)根据预测日的数值天气预报和训练好的回归模型进行风电功率的预测。
6 仿真实验与分析
对我国某风电场2012年2月4日以前20天的NWP数据和实测功率数据进行分析、建模和预测,NWP数据的时间间隔为15min。以2012年2月4日作为预测日,预测步长为一天(96个点)。NWP数据提供了风电场单位置的风速、风向、气温和气压四个信息。首先对于训练数据运用模糊减法聚类按天确定其聚类种数为三类,然后运用K均值聚类进行按天聚类。得其聚类中心分别为:
第1类:[0.986 7 0.244 7 0.545 3 -1.094 4 -0.7852 0.1702 0.1173];
第2类:[0.989 3 0.184 7 0.412 6 -1.181 8 -0.845 9 -0.093 5 -0.006 5];
第3类:[0.992 3 0.047 5 0.251 7 -0.895 4 -0.581 8 -0.008 3 -0.089 0]。
样本所属类别见表1。
表1 样本所属类别
Tab.1
| 样本日 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 类别 | 1 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 2 | 1 |
| 样本日 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 类别 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 1 |
预测日NWP向量为[0.980 8 0.340 0 0.800 9 -0.932 3 -0.579 5 0.112 7 -0.052 1],其与三个聚类中心的距离分别为0.418 4、0.594 0和0.636 2。所以本文中的模型训练数据选用第1类数据。
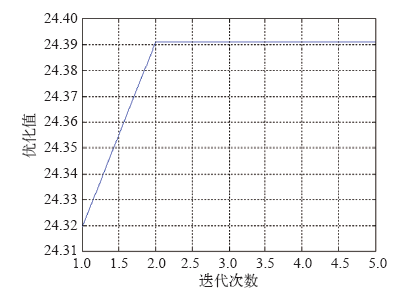
对于第1类数据,为方便处理,每个点的数据对象用5维向量表示为X = [V, Dcos, Dsin, T, P],其中的变量依次为每天每15min一个点的NWP数据归一化后的风速、风向余弦值、风向正弦值、气温、气压值。此处取支持向量机的核函数为RBF核函数,选取平均均方根误差的倒数为目标函数,以本文第5.3节中所述步骤进行AFSA-SVM预测模型建模,经人工鱼群算法优化后得到的支持向量机回归的参数为:惩罚参数C = 0.472 0;RBF核函数的参数r = 30.760 5。人工鱼群算法迭代过程中的最佳适应度曲线如图5所示。
图5
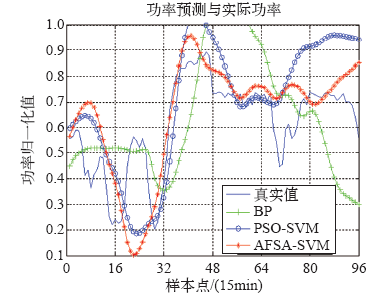
利用上述训练所得的AFSA-SVM模型和2012年2月4日的NWP提供的归一化后的数据进行风电功率预测,并与BP神经网络和粒子群算法(Particle Swarm Optimization,PSO)优化的SVM方法进行比较。图6为利用AFSA-SVM、PSO-SVM和BP三种模型进行风电功率预测时,实际值与预测值的基本趋势。
图6
表2 各种模型的MAE和RMSE对比
Tab.2
| 预测模型 | NMAE(%) | NRMSE(%) |
|---|---|---|
| BP神经网络模型 | 18.80 | 22.85 |
| PSO-SVM模型 | 15.26 | 18.27 |
| AFSA-SVM模型 | 11.34 | 15.73 |
7 结束语
针对风电功率预测精度有待提高的问题,采用风电场单位置历史NWP数据作为实验数据;考虑到SVM核函数参数r和错误惩罚因子C难以确定,提出了基于AFSA优化的SVM预测模型。结合实际风电场数据进行仿真实验验证,并与传统BP神经网络方法和PSO-SVM预测方法比较。实验结果表明,与PSO优化方法相比,FASA优化方法的学习能力更好;AFSA优化的SVM模型相比传统BP神经网络,其MAE降低了7.46%,RMSE降低了7.12%;与PSO-SVM模型相比,MAE和RMSE也分别下降了3.92%和2.54%。实验验证了AFSA优化的SVM模型有更好的预测效果。
参考文献
大规模风电并网对电力系统的影响及应对措施
[J].
Impact of large scale grid-connected wind power on power system and counter measures
[J].
考虑风电场布局以及风向角的风电功率预测
[J].
Wind power prediction considering wind farm layout and wind direction
[J].
基于相似日聚类的支持向量机风电功率预测方法
[J].
Wind Power Forecasting method based on similar day clustering of support vector machines
[J].
基于相似日聚类的神经网络风速预测
[C].
Neural network wind speed forecast based on similar day clustering
[C].
基于多位置NWP与主成分分析的风电功率短期预测
[J].
Wind power short-term prediction based on principal component analysis of multiple locations
[J].
基于遗传算法优化BP神经网络的风电功率预测
[J].
Wind power prediction based on genetic algorithm for optimization of BP neural network
[J].
基于改进粒子群优化算法的短期风电功率预测
[J].
Short term wind power prediction based on improved particle swarm optimization algorithm
[J].
基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测
[J].
Short term wind power prediction of the support vector regression based on the parameter optimization of the adaptive quantum behaved particle swarm optimization algorithm
[J].
支持向量在模式识别中的核函数特性分析
[J].
Support vector machine and kernel function characteristic analysis in pattern recognition
[J].
聚类分析中的若干问题
[J].
Some problems in cluster analysis
[J].
基于最小二乘支持向量机和人工鱼群算法的预应力锚杆布置间距优化
[J].
Range interval optimization of prestressed anchors based on the least squares support vector machine and artificial fish swarm algorithm
[J].