1 引言
在局部阴影条件下,光伏阵列的P-U曲线由单峰值变为多峰值,传统的最大功率点跟踪(Maximum Power Point Tracking,MPPT)方法因只能追踪到其中一个局部极值点而失效。局部阴影随时可能发生,大大降低了系统效率,因此,必须提出有效的多峰值情况下的全局MPPT方法。
针对该问题,国内外学者提出了多种多峰值情况下的MPPT方法,文献[3]采用并联功率补偿法,通过增加功率补偿单元消除多峰值现象,该方法简单可行,但系统结构复杂,成本较高。文献[4]采用复合MPPT算法,即先利用等效负载对最大功率点进行粗略定位,再利用传统单峰值MPPT方法进行精确跟踪。但等效负载法需要在线测量开路电压和短路电流,对光伏组件的参数依赖性较大,而传统单峰值MPPT方法稳态时功率振荡,增加功率损失。文献[5]采用斐波那契(Fibonacci)搜索法,该方法收敛速度较慢,实用性不强。近年来,粒子群优化(Particle Swarm Optimization,PSO)算法因算法简单,无需进行交叉和变异,在最大功率跟踪控制中得到应用[6,7,8,9],但传统粒子群优化算法搜索速度慢,随机参数多,存在陷入局部极值点的可能,应用过程中需要合理控制相关参数。
针对以上问题,本文提出了改进的粒子群(Improved Particle Swarm Optimization,IPSO)算法,该算法以占空比为粒子,初始化将粒子均匀分散在可能的功率极值点处,缩小搜索范围,防止陷入局部极值点。本算法对传统的PSO进行了三点改进:
(1)传统的PSO目标函数是固定阴影模式下的功率表达式,适用条件有限,本算法目标函数是根据实时电压电流计算的功率,不需要温度传感器和光照传感器,也不需提前了解光伏系统的阴影情况,适合任何阴影条件下的光伏阵列。
(2)根据迭代次数线性调整惯性权重和学习因子,加强算法的全局搜索能力,使收敛更加平稳。
(3)将反正切函数应用到粒子的速度更新中,单独限制每个粒子的速度,减小迭代过程中的振荡,加快收敛速度。改进后的粒子群算法能对参数进行合理调节,提高跟踪效率和算法的有效性。
2 光伏阵列的多峰值特性分析
光伏系统的安装架构有很多种,集中式结构由于电路成本低而得到广泛应用。但集中式结构光伏电池板面积较大,较容易受外界遮挡出现局部阴影问题,影响光伏发电的效率。
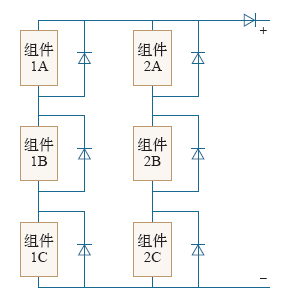
图1
表1 四种不同的工作模式
Tab.1
| 模式 | 组件1A | 组件1B | 组件1C | 组件2A | 组件2B | 组件2C |
|---|---|---|---|---|---|---|
| 光照强度/(W/m2) | ||||||
| 模式1 | 1 000 | 400 | 200 | 1 000 | 800 | 600 |
| 模式2 | 1 000 | 400 | 200 | 1 000 | 1 000 | 1 000 |
| 模式3 | 1 000 | 1 000 | 200 | 1 000 | 1 000 | 1 000 |
| 模式4 | 1 000 | 1 000 | 1 000 | 1 000 | 1 000 | 1 000 |
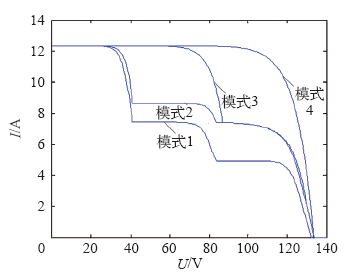
图2
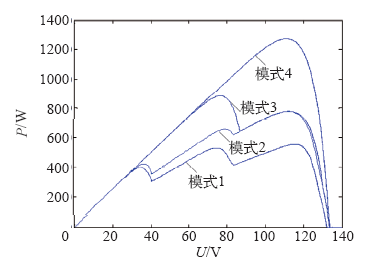
图3
(1)阴影条件下,对于m个串联模块的光伏阵列,最多存在m个最大功率峰值点。
(2)光伏阵列串联子列局部阴影会导致功率多峰值点,并联子列不会引起多峰值现象,只会引起功率损失。
(3)光伏阵列的P-V曲线的多峰值发生在0.8倍的光伏组件开路电压的整数倍,即0.8Uoc_moudle。
以上述结论为依据,提出了改进的粒子群算法。
3 IPSO算法在MPPT中的应用
3.1 粒子群算法
粒子群算法是启发式算法的一种,有较强的全局搜索能力。将每个可能最优结果产生的解表述为群体中的一个粒子,每个粒子都有速度矢量、位置矢量和由目标函数决定的适应度。在每次迭代过程中,通过计算目标函数并进行比较,进而确定当前时刻每个粒子的个体最优值Pi和全局最优值Pg,按照式(1)确定下一时刻粒子的位置,按照式(2)确定下一时刻粒子的速度[10]。
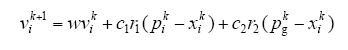
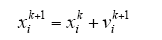
个体最优值更新的计算式为
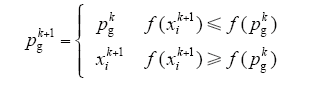
全局最优值更新的计算式为
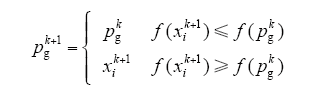
式中,w是惯性权重,保持运动惯性;c1、c2是学习因子;r1、r2是相互独立的随机数,服从[0 1]上均匀分布;i是第i个粒子;k是迭代次数;xik是第k次循环中第i个粒子的位置;pgk第k次循环的全局最优值;pik第k次循环的第i个粒子的个体最优值。
3.2 改进的PSO算法的MPPT
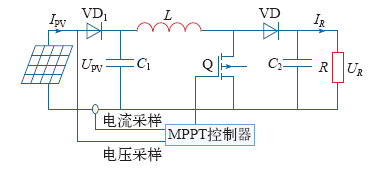
由Boost变换器的输入输出关系可知
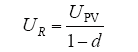
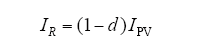
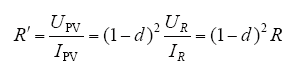
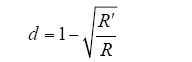
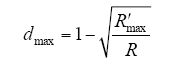
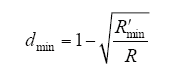
式中,R′为Boost电路的等效电阻;R为负载电阻;dmin、dmax分别为变换器的最小和最大占空比。
图4
由式(7)可知,通过调节占空比d可使Boost电路的等效电阻与光伏等效电阻相匹配,从而实现最大功率跟踪。将占空比直接作为粒子,则式(2)变为
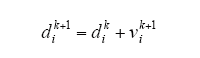
为使粒子位置不超过占空比d可调的区间[0 1],通常对速度参数vi进行控制。在文献[11]中,限制粒子速度的最大阈值为0.035,但这种方法不能区分不同粒子,将导致较长的跟踪时间。本文采用反正切函数来保证粒子速度在安全阈值范围内,同时粒子具有更高的速度。反正切函数描述的粒子速度公式为
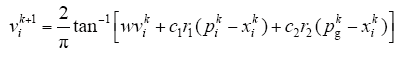
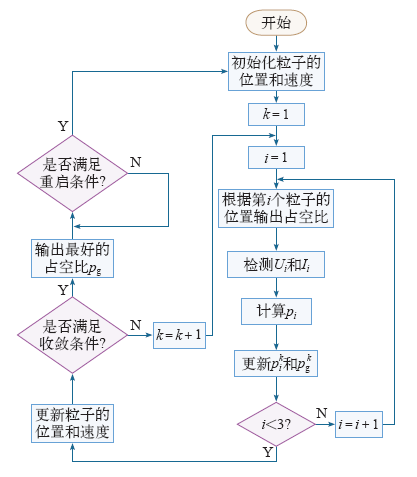
本文提出的改进型PSO算法的流程图如图5所示,算法的具体设置如下:
(1)粒子数目的选择。选择占空比d直接作粒子,由于粒子数目多少直接影响算法的收敛速度和求解精度,为了提高算法的有效性,必须合理设置粒子数目。经文献和仿真验证,对于m个串联模块的光伏阵列,最多存在m个功率极值点,因此粒子的个数设置为光伏阵列的串联支路数m。
图5
(2)初始粒子位置的选择。粒子的初始位置可以随机分布也可以放置在固定位置,在初始阶段如果将粒子的位置设定在理论的最大功率极值点,将会大大缩短搜索时间。仿真证明功率峰值点对应的电压值间隔约为0.8Uoc_module,光伏阵列可能的极值点对应的最小和最大电压近似0.8Uoc_module和0.8Uoc_array.,对应的Boost电路的等效电阻为R′min和R′max,根据式(9)、式(10),可以确定dmin和dmax。粒子的初始位置等间距放置在[dmindmax]区间。
(3)适应度函数。选择光伏阵列总功率为适应度函数,通过采样粒子的电压、电流计算适应度P = UI,为保证准确采样,粒子估计的时间间隔应大于变换器的稳定时间。
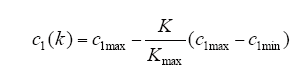
(4)参数调整。惯性权重w、自身认知因子c1、社会认知因子c2的选择对算法的计算过程影响很大,w决定粒子继承飞行速度,影响算法的收敛。为加快算法收敛速度,w应随着迭代的进行对速度的影响越来越小。在算法的初始阶段,设置较大的惯性权重w,使算法不容易陷入局部最优,随着迭代的进行,逐渐减小w使算法具有较强精准搜索能力。自身认知因子c1和社会认知因子c2决定了粒子飞行的方向。当c1>c2时,向个体最优的方向靠近,而c1<c2时,向全局最优值的方向靠近。本算法中,c1、c2分别定义为线性递减和线性递增的函数,本文通过迭代次数线性调整w、c1、c2,即
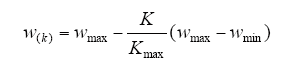
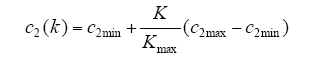
(5)终止条件。使用双收敛准则避免多次迭代带来的最大功率点附近振荡问题。初始时粒子位置比较分散,当追踪到最大功率点,所有粒子位置比较集中,粒子的位置标准差比较小,或如果达到最大迭代次数,则MPPT算法停止,并输出最优解。判断条件为
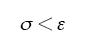
式中,σ为粒子位置标准差;ε为设定的阈值。
(6)重启条件。最大功率点随着外界条件的变化而变化,当阴影状况发生变化时,终止的算法需要重新启动,以便追踪到新的最大功率点。重新初始化条件为
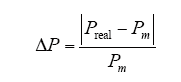
4 仿真分析
为了证明所提算法的有效性,在Matlab/Simulink环境搭建光伏阵列MPPT控制的仿真模型,MPPT模块使用S-Function函数编写,其输入为光伏阵列的输出电压U和电流I,输出为占空比d。仿真时以调用M文件的方式调用粒子群算法程序,并通过改变光照条件模拟阴影遮挡情况。设占空比d为粒子的位置,变化量Δd为粒子的速度,占空比d和变化量Δd按照式(11)、式(12)更新,根据适应度函数找出最优占空比dbest,进而找到最大功率点。
仿真模型的参数设置为:C1 = 200μF,C2 = 200μF,L = 0.15mH,Boost电路的开关频率取50kHz,改进型粒子群算法实现MPPT功能的参数设置见表2。
表2 IPSO的参数设置
Tab.2
| 参数 | 取值 | 参数 | 取值 | |
|---|---|---|---|---|
| 粒子个数 | 3 | wmax | 1 | |
| 占空比最小值 | 0.1 | wmin | 0.1 | |
| 占空比最大值 | 0.9 | c1min | 2 | |
| 采样时间 | 0.04 | c1max | 1 | |
| 迭代次数 | 30 | c2min | 2 | |
| 收敛条件ε | 0.002 | c2max | 1 |
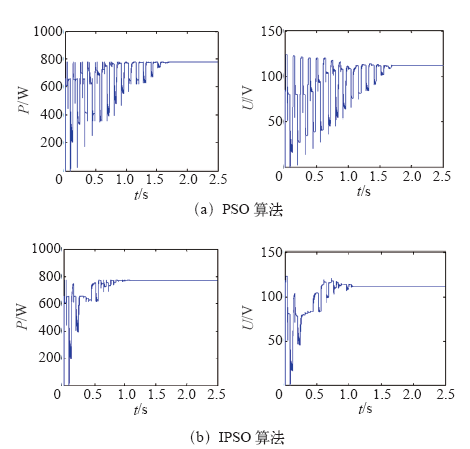
(1)阴影不变情况下的仿真。为了对比基本PSO算法与IPSO算法,当光伏阵列处于工作模式2时,仿真结果如图6所示。
图6
图6
传统粒子群算法和改进粒子群算法的对比
Fig.6
Comparison of the traditional PSO algorithm and IPSO algorithm
图6表明,针对部分阴影条件下的光伏阵列,两种算法均能有效追踪到全局最大功率点并稳定下来,IPSO算法的跟踪速度快,动态响应振荡较小。改进后的粒子群算法在1.04s时跟踪到最大功率点为774.7W,基本粒子群算法在1.68s时,跟踪到最大功率点为773.3W,通过对比发现,IPSO算法的追踪时间缩短了0.64s。
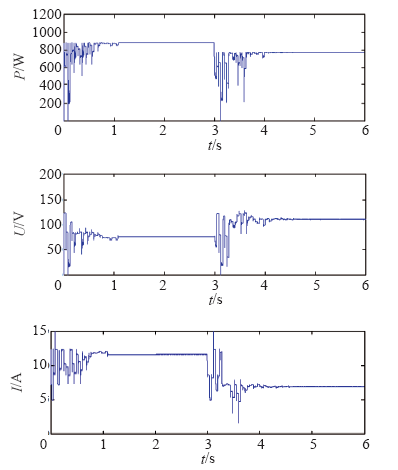
(2)阴影突变情况下的仿真。当阴影情况发生变化时,需要重新启动粒子群算法使系统稳定在新的最大功率点,图7为阴影情况从工作模式3突变为工作模式2改进型粒子群算法的仿真结果,粒子在1.08s找到工作模式3下的最大功率点882.76W,算法终止迭代稳定输出追踪到的最大功率,3s时阴影情况发生变化,满足式(14),算法重启,在4.68s时稳定工作在新的最大功率点为774.98W,成功实现阴影突变情况下的最大功率点跟踪。
图7
图7
阴影突变情况下光伏阵列的输出特性曲线
Fig.7
Output waveforms of PV array under changed shading case
5 结束语
本文提出了一种改进型粒子群算法,以变换器的占空比为粒子,初始化将粒子均匀分散在可能的极值点处,线性调整惯性权重、学习因子,并通过引入反正切函数,对传统的粒子群速度更新进行修改,单独限制每个粒子的速度。改进后的粒子群算法收敛速度快,跟踪过程的振荡较小,阴影变化时能快速跟踪到新的最大功率点。
参考文献
部分遮蔽光伏发电系统的建模及MPPT控制
[J].
Analytical modeling and maximum power point tracking control of partially shaded photovoltaic generation system
[J].
考虑局部阴影条件下光伏系统MPPT控制研究
[D].
A study on a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions
[C].
Control characteristics of a Fibonacci search based maximum power point tracker when a photovoltaic array is partially shaded
[C].
基于改进PSO的复杂环境下光伏MPPT控制
[J].
PVMPPT control in complex environment based on improved PSO algorithm
[J].
基于改进PSO算法的光伏阵列MPPT研究
[J].
Research on MPPT control for PV array based on promoted PSO algorithm
[J].
A particle swarm optimization-based maximum power point tracking algorithm for PV systems operating under partially shaded conditions
[J].
Maximum power point tracking of multiple photovoltaic arrays: a PSO approach
[J].
A deterministic particle swarm optimization maximum power point tracker for photovoltaic system under partial shading condition
[J].