电气工程学报, 2015, 10(9): 35-40 doi: 10.11985/2015.09.006

电气工程新技术专刊——本专刊由沈阳工业大学电气工程学院供稿，组稿人为张凤阁教授

基于模糊控制的无刷双馈发电机直接功率控制策略

金石, 任新凯

沈阳工业大学电气工程学院 沈阳 110870

Direct Power Control Strategy Based on Fuzzy Control of Brushless Doubly-Fed Generator

Jin Shi, Ren Xinkai

Shenyang University of Technology Shenyang 110870 China

责任编辑: 崔文静

收稿日期: 2015-07-28   网络出版日期: 2015-09-25

基金资助: 国家自然科学基金项目.  51277124
国家自然科学基金项目.  51537007
高等学校博士学科点专项科研基金资助课题.  20122102110004

Received: 2015-07-28   Online: 2015-09-25

作者简介 About authors

金 石 女 1981年生,博士,讲师,研究方向为电力电子及电力传动。

任新凯 男 1988年生,硕士研究生,研究方向为电力电子及电力传动。

摘要

为了对无刷双馈发电机的有功功率和无功功率进行实时有效控制,采用了直接功率控制策略。与矢量控制方法相比,直接功率控制不需要复杂的坐标变换,可简化控制系统,提高系统的响应速度。为克服传统的直接功率控制方法中无法根据功率、磁链的大小来快速准确地选择合适的电压矢量这一缺点,提出了基于模糊控制的无刷双馈发电机直接功率控制策略,采用了新型模糊控制器代替传统的有功功率和无功功率两点式Bang-Bang控制,根据功率误差的大小,实现了大误差大调节、小误差精调节的策略。文中采用转子速模型实现了有功功率和无功功率的解耦,因此可以对有功功率和无功功率进行独立控制,进而实现了对功率因数的控制。在Matlab/Simulink软件中建立仿真模型,仿真结果表明,基于模糊控制的直接功率控制策略不仅可以提高控制精度,还可以提高电机对功率指令的响应速度,保证运行的稳定性,证明了本文控制策略的有效性和正确性。

关键词： 无刷双馈 ; 模糊控制 ; 发电机 ; 直接功率控制

Abstract

In order to achieve real-time effective control of active power and reactive power for brushless doubly-fed generator (BDFG), we put forward a direct power control (DPC)strategy. Compared with the traditional vector control, DPC without complex coordinate conversion simplifies the control system and improves the response speed of the system. The traditional DPC uses power hysteresis comparator to achieve the purpose of power control. However, we replace traditional power hysteresis comparator with fuzzy controller, because this method can select the appropriate voltage vector according to the size of the active power and reactive power degree, so it can improve control accuracy and boost motor response speed to power command.The BDFG used in wind power generation control system with the direct power control based on the fuzzy rule is simulated by using the Matlab/Simulink software, and the simulation results show that the control method is correct and effective.

Keywords： Brushless doubly-fed ; fuzzy control ; generator ; direct power control

PDF (2582KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

金石, 任新凯. 基于模糊控制的无刷双馈发电机直接功率控制策略. 电气工程学报[J], 2015, 10(9): 35-40 doi:10.11985/2015.09.006

Jin Shi, Ren Xinkai. Direct Power Control Strategy Based on Fuzzy Control of Brushless Doubly-Fed Generator. Journal of Electrical Engineering[J], 2015, 10(9): 35-40 doi:10.11985/2015.09.006

1 引言

随着人类对能源的需求急剧增加,而化石能源供应却日益紧张,环境问题愈加突出,风能作为一种清洁的可再生能源,受到世界各国的重视。其蕴量巨大,比地球上可开发利用的水能总量还要大10倍。近年来,风能市场迅速发展起来。无刷双馈发电机（Brushless Doubly-Fed Generator,BDFG）是一种新型交流电机,它兼有异步电机和同步电机的共同优点,不仅结构坚固、运行可靠且易于维护,可以在无刷情况下实现双馈运行,而且具有转速和功率因数可调、变频器容量小及系统成本低等特点。因此,BDFG 在大容量的风力发电和水力发电系统中具有广阔的发展前景,成为近年来的研究热点之一。

目前国内外一些文献将直接功率控制（Direct Power Control,DPC）技术应用于发电机的有功和无功功率的解耦控制。文献[1]提出将DPC技术应用到双馈风力发电系统机侧变换器及双馈风力发电机（DFIG）控制中。根据DFIG的动态数学模型,推导和分析了DFIG转子侧变换器电压矢量对定子输出有功和无功功率变化的影响,提出了一种开关频率恒定的空间矢量脉宽调制（SVPWM）–DPC策略。该控制策略将SVPWM技术与DPC相结合,实现DFIG有功和无功功率的解耦控制与功率因数任意可调,具有良好的动、静态特性。文献[2]研究了电网电压不平衡条件对直接功率控制的影响并进行了详尽的分析,针对网侧变换器和转子侧变换器提出了3个控制目标,即获得正弦、对称的电网电流（定子电流）,获得恒定的无功功率和获得恒定的有功功率。经过分析得到为完成上述3个控制目标所需的功率补偿指令,得到了无需提取负序电流的基于给定功率指令补偿的改进直接功率控制策略。文献[3]介绍了无刷双馈电机的有功功率、无功功率以及转矩等特性与控制绕组电压、控制绕组频率以及功角有关,并给出了各个状态下的特性图。

由于BDFG是一种新型电机,具有非线性、强耦合性等特点[4,5],因此对其控制比传统电机要复杂的多。目前BDFG的直接功率控制方法,采用有功功率和无功功率两点式滞环比较来实现功率控制,控制性能受容差大小的影响非常大,不能根据功率的误差大小来选择合适的电压矢量。为了解决以上问题,本文提出了一种适用于BDFG的基于模糊控制的直接功率控制方法,该控制方法根据BDFG的有功功率和无功功率误差大小选择合适的电压矢量,实现了功率大偏差大调解、小偏差小调节,提高了控制精度,控制系统简单易实现,且计算量小,动态响应速度快[6]。

2 无刷双馈发电机（BDFG）运行原理

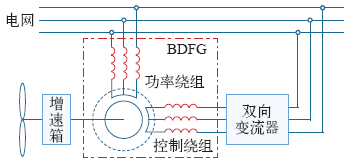
无刷双馈发电机工作原理如图1所示。定子绕组由两套极对数不等（pp≠pc）的三相对称绕组构成,分别称为功率绕组和控制绕组。它们可以是由彼此独立的两套绕组组成,也可由1套三相绕组通过变极联结获得两种不同极数的三相对称绕组。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   无刷双馈发电机工作原理图

Fig.1   Principle diagram of brushless doubly fed generator


功率绕组接入电网、控制绕组通过变频器接入电网后,由于两套定子绕组同时有电流流过,因此在气隙中产生两个不同极对数的磁场,这两个磁场通过转子的调制发生交叉耦合,构成了实现能量传递转换的基础,经分析可得稳态运行时电机的转速与pp、pc、fp及fc的关系为

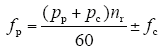
式中,fp、fc分别为电网工频和变频器输出频率,pp、pc分别为功率绕组和控制绕组的极对数。

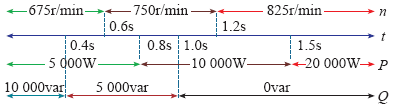
当发电机超同步运行时,fc前取负号表示控制绕组与功率绕组同相序,转子上的机械功率一部分通过功率绕组输送给电网,另一部分通过控制绕组侧变频器向电网回馈电能;当发电机亚同步运行时,fc前取正号表示两个绕组外加电源相序相反,转子上的机械功率和控制绕组通过变频器从电网吸收的电磁功率转化为功率绕组侧电磁功率输送给电网;fc = 0时,无刷双馈电机的转速称为自然同步转速,功率绕组和控制绕组从转子上吸收的机械功率除去损耗后转化为功率绕组侧的电磁功率输送给电网,控制绕组通过变频器从电网吸收的电磁功率基本为零。可见无刷双馈发电机可通过改变与控制绕组相连的变频器的输出频率来调节功率绕组侧的输出频率,实现变速恒频发电。

3 BDFG的数学模型

在本文中,BDFG采用转子速坐标系数学模型,数学模型如式（2）、式（3）和式（4）所示。

BDGM在转子速dq坐标系下[7],电压矩阵方程在状态变量为定子、转子绕组的电流时为

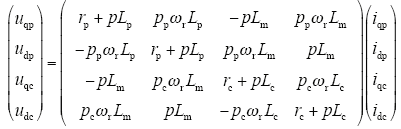
功率绕组和控制绕组磁链方程

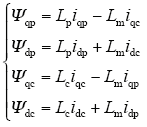
根据瞬时功率理论,可以得知BDFG的瞬时有功功率和无功功率的表达式

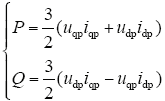
式中,p为微分算子;rp、rc分别为功率绕组和控制绕组的电阻;Lp、Lc和Lm分别为功率绕组自感、控制绕组自感和功率绕组与控制绕组的互感;ωr为转子机械角速度;其中下标带有p表示功率绕组;下标带有c表示控制绕组;q,d表示dq坐标下q轴和d轴分量。

4 基于模糊控制的BDFG直接功率控制

4.1 基于模糊控制的BDFG直接功率控制原理

基于模糊的直接功率控制的控制思想源于直接功率控制（DPC）[8,9,10,11],并结合了模糊控制理论[12,13,14]。它不需要复杂坐标变换和电流内环,不再采用功率滞环,而是用模糊控制器取代滞环比较器,可以大大提高对功率控制的精度,而且还提升了系统的动态响应速度,其控制原理框图如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

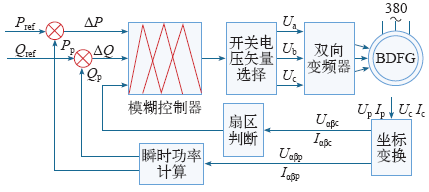
图2   基于模糊控制的BDFG直接功率控制原理框图

Fig.2   Direct power control based on fuzzy control of BDFG


混合转子BDFG的电磁转矩也可以由功率绕组和控制绕组的磁链来表示

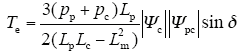
式中,Ψc为控制绕组磁链;Ψpc为功率绕组和控制绕组的互感磁链;δ为Ψc和Ψpc之间夹角。

磁链的表达式为

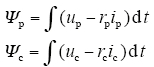
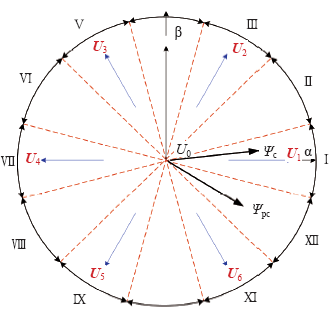
Ψpc与Ψp成正比,因为定子功率绕组与电网直接相连,功率绕组磁链幅值Ψp约等于常数,所以功率绕组和控制绕组的互感磁链Ψpc也为常数,而且在大型BDFG中,在忽略铜耗的情况下,瞬时电磁功率与输出功率大致相等,即Pe ≈ Pout。因此,可以改变控制绕组磁链Ψc和两套绕组磁链间夹角δ来控制有功功率和无功功率的变化。为了提高控制精度,把空间平面分为12个扇区,如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   扇区和电压矢量

Fig.3   Sector and voltage vector


通过改变Ψpc和Ψc之间的夹角δ来改变有功功率P大小,δ变大则P增大,反之亦然;无功功率Q的控制可以通过直接控制Ψc的幅值实现,增大Ψc的幅值意味着大量的无功功率将由变流器馈送,因此,功率绕组上产生的无功功率Qp将随之减少。DPC策略要保证同时控制有功功率和无功功率,这样,在同一时刻选择的电压矢量不仅要满足有功功率,同时也要满足无功功率的调节需求。因此,在某一固定时刻,所需选择的电压矢量就唯一确定了。例如,当控制绕组磁链Ψc处于第一扇区时,需要增加有功功率,减小无功功率,为了同时满足这两个要求,只可以选择电压矢量U2。

4.2 模糊控制器的设计

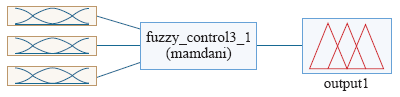
模糊控制器结构如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   模糊控制器结构

Fig.4   The structure of fuzzy controller


在本文中,模糊控制器的输入是有功功率误差ΔP、无功功率误差ΔQ和控制绕组磁链所处扇区S。输出为逆变器的8个开关状态,因为这8种开关状态本身是准确量,所以不需要进行模糊化。在模糊控制器中,这8种开关状态用其所对应的十进制数来表示。在有功功率误差ΔP的论域上定义了3个模糊子集,在无功功率误差ΔQ的论域上定义了3个模糊子集,在控制绕组磁链所处扇区S的论域上定义了12个模糊子集,这更加细化了误差的大小。

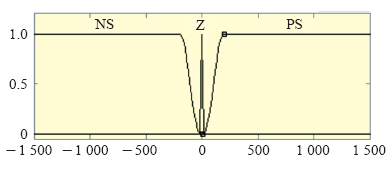
有功功率误差ΔP的论域为{NS,Z,PS},分别表示负、基本不变、正。其输入值取值范围是[-1 500,1 500]。图5为有功功率误差的隶属函数。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   有功功率误差的隶属函数

Fig.5   Subordinating degree function of active power error


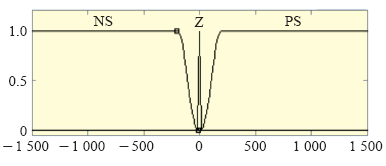
无功功率误差ΔQ的论域为{NS,Z,PS},分别表示负、基本不变、正。其输入值取值范围是[-1 500,1 500]。图6为无功功率误差的隶属函数。因为对有功功率和无功功率的控制同等重要,所以把它们的隶属度函数设置成一样。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   无功功率误差的隶属函数

Fig.6   Subordinating degree function of reactive power error


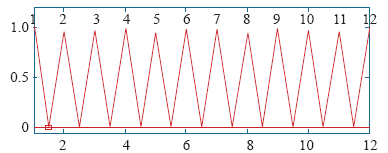
控制绕组磁链所处扇区S的论域为{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12},表示磁链所在的区段。输入取值范围是[1, 12]。图7为磁链位置角隶属函数。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   磁链位置角隶属函数

Fig.7   Subordinating degree function of flux position angle


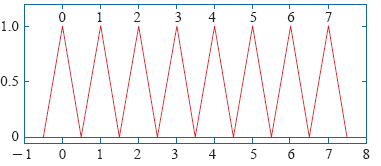
图8为模糊控制器输出隶属函数。控制器输出论域为{0, 1, 2, 3, 4, 5, 6, 7},为了便于设计,这里定义：U0[000]、U1[100]、U2[110]、U3[010]、U4[011]、U5[001]、U6[101]、U7[111]。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   模糊控制器输出隶属函数

Fig.8   Subordinating degree function of the output of fuzzy controller


4.3 模糊控制规则表设计

在上文中,已将控制绕组磁链圆划分为12个扇区,在此基础上,根据电压矢量表作出选择。因此可以很方便地判断出不同扇区,得到如表1所示的模糊控制规则表。

表1   模糊控制规则表

Tab.1  Rules table of fuzzy control

ΔPΔQS1S2S3S4S5S6
NSNSU6U1U1U2U2U3
ZU6U1U1U2U2U3
PSU5U5U6U6U1U1
ZNSU2U2U3U3U4U4
ZU0U0U7U7U0U0
PSU4U4U5U5U6U6
PSNSU2U2U3U3U4U4
ZU2U2U3U3U4U4
PSU3U4U4U5U5U6
ΔPΔQS7S8S9S10S11S12
NSNSU3U4U4U5U5U6
ZU3U4U4U5U5U6
PSU2U2U3U3U4U4
ZNSU5U5U6U6U1U1
ZU7U7U0U0U7U7
PSU1U1U2U2U3U3
PSNSU5U5U6U6U1U1
ZU5U5U6U6U1U1
PSU6U1U1U2U2U3

新窗口打开| 下载CSV


5 基于模糊控制的BDFG直接功率控制系统仿真

为了验证上述控制策略的有效性,本文基于Matlab/Simulink 平台建立了无刷双馈发电机直接功率控制系统仿真模型,其相关参数见表2。

表2   无刷双馈发电机参数

Tab.2  Parameters of BDFG

参 数数 值
功率绕组极对数3
控制绕组极对数1
功率绕组电阻/Ω0.166 2
控制绕组电阻/Ω0.188 2
功率绕组自感/mH17.37
控制绕组自感/mH23.51
定子绕组互感/mH18.13
转动惯量/（kg.m2）0.3

新窗口打开| 下载CSV


Simulink仿真采用ode45算法,仿真总时间设为2s,发电机给定的转速发生阶跃变化,发电机分别在亚同步、同步和超同步模式运行;给定的有功功率和无功功率也随时间发生3次变化,最后实现单位功率因数运行。给定随时间变化的关系如图9所示。仿真结果如图10所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   给定条件随时间变化关系

Fig.9   Given conditions change with time


图10

新窗口打开| 下载原图ZIP| 生成PPT

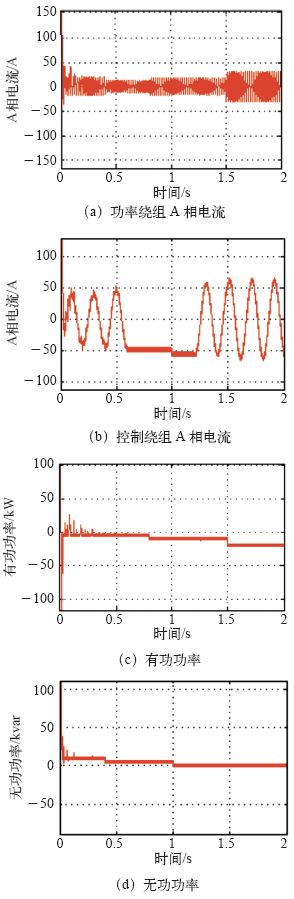
图10   基于模糊控制的BDFG直接功率控制系统仿真结果

Fig.10   Simulation results of BDFG direct power system control based on fuzzy control


由图10的仿真结果可知,在整个仿真过程中,控制绕组频率随电机转速不同而自动调节,当BDFG的转速变化时,直接功率控制策略输出的有功功率和无功功率完全跟随给定,不受转速变化的影响,实现了有功功率和无功功率独立调节,并具有很快的响应速度。当有功功率增加时,功率绕组电流也随之增大,响应速度快,且没有超调。当无功功率减小到0var时,控制绕组的电流明显增加,而功率绕组电流稍微减小。可见,无功功率已经全部由控制绕组馈送,功率绕组上只输出有功功率。基于模糊控制的直接功率控制方法可以使功率的调节更为精确,降低功率调节误差。在整个仿真过程中,控制绕组频率根据电机转速不同而自动调节,保证功率绕组输出的电流频率始终为50Hz,可见,基于模糊控制的直接功率控制方法适合用于BDFG系统。

6 结论

本文首先对BDFG工作原理进行了分析,在BDFG转子速数学模型的基础上搭建了仿真模型,并对基于模糊控制的直接功率控制策略进行了仿真,得出以下结论：

（1）基于转子速模型建立的DPC控制策略,不需要复杂的坐标变换,易于实现。

（2）基于模糊控制的直接功率控制策略可以提高功率控制精度。

（3）基于模糊控制的直接功率控制策略能够对BDFG功率绕组上输出的有功功率和无功功率进行实时有效的独立控制。

参考文献

葛凯, 阮毅, 赵梅花 , 等.

双馈风力发电机系统机侧直接功率控制

[J]. 电力电子技术, 2014,48(4):50-53.

[本文引用: 1]

Ge Kai, Ruan Yi, Zhao Meihua , et al.

Study of direct power control for rotor-side converter double-fed wind power generation system

[J]. Power Electronics, 2014,48(4):50-53.

[本文引用: 1]

尚磊, 孙丹 .

双馈异步风力发电系统改进直接功率控制策略研究

[D]. 浙江:浙江大学, 2011.

[本文引用: 1]

韩力, 罗杰, 王华 .

无刷双馈电机稳态数学模型和运行特性分析

[J]. 重庆大学学报, 2013,36(8):61-67.

URL     [本文引用: 1]

To further study the steady-state characteristics of brushless doubly-fed machine(BDFM) with squirrel-rotor，the basic equations are given according to the coupling circuits of BDFM. And then，the mathematical models of BDFM current，active power，reactive power，electromagnetic torque and power factor are analyzed and derived respectively. Furthermore，the characteristics of torque-angle，torque-frequency，power-angle，reactive power，power factor and V-shaped curve of BDFM are obtained respectively by MATLAB simulation of a prototype. The energy conversion of BDFM is analyzed by the proposed mathematical models at the same time. The results show that all the steady-state characteristics of BDFM can be expressed as the functions of the control windings voltage，frequency and the power angle. The proposed model simplifies the analysis of the steady-state characteristics of BDFM and provides a theoretical foundation for the further study on operating stability and control strategy of BDFM.

Han Li, Luo Jie, Wang Hua .

Analysis on stead state mathematical models and operating characteristics of brushless doubly-fed machine

[J]. Journal of Chongqing University, 2013,36(8):61-67.

URL     [本文引用: 1]

To further study the steady-state characteristics of brushless doubly-fed machine(BDFM) with squirrel-rotor，the basic equations are given according to the coupling circuits of BDFM. And then，the mathematical models of BDFM current，active power，reactive power，electromagnetic torque and power factor are analyzed and derived respectively. Furthermore，the characteristics of torque-angle，torque-frequency，power-angle，reactive power，power factor and V-shaped curve of BDFM are obtained respectively by MATLAB simulation of a prototype. The energy conversion of BDFM is analyzed by the proposed mathematical models at the same time. The results show that all the steady-state characteristics of BDFM can be expressed as the functions of the control windings voltage，frequency and the power angle. The proposed model simplifies the analysis of the steady-state characteristics of BDFM and provides a theoretical foundation for the further study on operating stability and control strategy of BDFM.

张凤阁, 王秀萍, 贾广隆 .

无刷双馈电机复合转子参数的优化设计

[J]. 电工技术学报, 2014,29(1):77-84.

URL     [本文引用: 1]

Brushless doubly fed machine of have promising application prospect in VSCF wind power generation and energy-efficient drive field. Coupling capability of rotor is the important factor affecting power density. A novel rotor is presented, that is composite rotor including magnetic barriers and short-circuit cage. Using finite element method, the key parameters affecting the coupling capability are analyzed, such as pole arc factor, magnetic layer numbers, ratio of magnetic and non-magnetic, short-circuit ring, short-circuit set numbers and short-circuit layer numbers. This novel rotor is a promising rotor, which has simple structure, process convenience, stronger coupling capability and higher output torque density. Experiments were carried out to verify. This paper provides theoretical basis for designing novel rotor.

Zhang Fengge, Wang Xiuping, Jia Guanglong .

Optimum design for composite rotor structural parameters of brushless doublv fed machines

[J]. Transactions of China Electrotechnical Society, 2014,29(1):77-84.

URL     [本文引用: 1]

Brushless doubly fed machine of have promising application prospect in VSCF wind power generation and energy-efficient drive field. Coupling capability of rotor is the important factor affecting power density. A novel rotor is presented, that is composite rotor including magnetic barriers and short-circuit cage. Using finite element method, the key parameters affecting the coupling capability are analyzed, such as pole arc factor, magnetic layer numbers, ratio of magnetic and non-magnetic, short-circuit ring, short-circuit set numbers and short-circuit layer numbers. This novel rotor is a promising rotor, which has simple structure, process convenience, stronger coupling capability and higher output torque density. Experiments were carried out to verify. This paper provides theoretical basis for designing novel rotor.

王凤翔, 张凤阁 . 磁场调制式无刷双馈交流电机[M]. 吉林: 吉林大学出版社, 2004.

[本文引用: 1]

郭忠林 .

基于双模糊理论的异步电机直接转矩控制系统研究

[D]. 成都:西华大学, 2008.

[本文引用: 1]

赵荣理, 王昕, 张爱玲 .

无刷双馈电机数学模型的研究和分析

[J]. 微特电机, 2013,41(7):18-23.

[本文引用: 1]

Zhao Rongli, Wang Xin, Zhang Ailing .

Research and analysis on brushless doubly fed machine mathematical models

[J]. Micro Motor, 2013,41(7):18-23.

[本文引用: 1]

贺子倩 .

变速恒频双馈风力发电系统改进直接功率控制策略

[D]. 杭州:浙江大学, 2012.

[本文引用: 1]

Hu Jiabing, Nian Heng, Hu Bin , et al.

Direct active and reactive power regulation of DFIG using sliding mode control approach

[J]. IEEE Transactions on Energy Conversion, 2010,25(4):1028-1039.

DOI:10.1109/TEC.2010.2048754      URL     [本文引用: 1]

Zhi Dawei, Xu Lie, Williams B W .

Model-based predictive direct power control of doubly fed induction generators

[J]. IEEE Transactions on Power Electronics, 2010,25(2):341-351.

DOI:10.1109/TPEL.2009.2028139      URL     [本文引用: 1]

Abad G, Rodriguez M A, Iwanski G , et al.

Direct power control of doubly-fed-induction-generator-based wind turbines under unbalanced grid voltage

[J]. IEEE Transactions on Power Electron, 2010,25(2):442-452.

DOI:10.1109/TPEL.2009.2027438      URL     [本文引用: 1]

席爱民 . 模糊控制技术[M]. 西安: 西安电子科技大学出版社, 2008.

[本文引用: 1]

王季方, 卢正鼎 .

模糊控制中隶属度函数的确定方法

[J]. 河南科学, 2000,18(4):348-351.

[本文引用: 1]

Wang Jifang, Lu Zhengding .

The determine method of membership function in fuzzy control

[J]. Henan Science, 2000,18(4):348-351.

[本文引用: 1]

诸静 . 模糊控制理论与系统原理[M]. 北京: 机械工业出版社, 2005.

[本文引用: 1]

/

〈 〉