电气工程学报, 2015, 10(8): 45-49 doi:

理论研究

基于线圈倾斜方法的永磁同步直线电机推力波动抑制研究

李乐, 董菲, 赵吉文, 苏云升, 盘真保

安徽大学电气工程与自动化学院 合肥 230601

The Study of Reduction of the Thrust Ripple According to Coil Arrangement in PMLSM

Li Le, Dong Fei, Zhao Jiwen, Su Yunsheng, Pan Zhenbao

责任编辑: 崔文静

收稿日期: 2015-06-24   网络出版日期: 2015-08-25

基金资助: 国家自然科学基金资助项目.  51277002

Received: 2015-06-24   Online: 2015-08-25

作者简介 About authors

李 乐 男 1991年生,硕士,研究方向为永磁同步直线电机设计与控制。

董 菲 女 1984年生,讲师,研究方向为电机分析与设计。

摘要

采用线圈倾斜方法,设计了一种无铁心双次级永磁同步直线电机,实现对推力波动的抑制。首先,分析了由于线圈倾斜带来的负面影响及应对策略,设计了线圈倾斜结构;其次,根据电机的几何模型,建立了3D有限元模型,仿真计算了电机的瞬时推力,并进行了谐波分析;最后,以谐波畸变率为参考指标,对比分析了线圈一端倾斜距离由0mm变为23mm的一组电机模型,证明了倾斜距离为19mm（极距）时,电机的推力波动最小,验证了此种方法的有效性。

关键词： 永磁同步直线电机 ; 线圈倾斜 ; 推力波动 ; 谐波 ; 3D有限元

Abstract

In order to reduce thrust ripple of permanent magnet linear synchronous motor (PMLSM), an ironless PMLSM is designed in which the coil is skewing. A 3D FEM model is built based on the geometric model to simulate the transient thrust of PMLSM and analyse the higher harmonics. Different skewing length of the coil is compared and analysed according considering their THD, the result shows a minimum thrust ripple is get when the skewing length is 19mm(pole pitch). Negative effects such as weaken of the thrust, caused by the skew of the coil are considered. The method extending the length of the permanent magnet is used to compensate the negative effects. The simulation results prove the validity of this method.

Keywords： PMLSM ; skew of coil ; thrust ripple ; harmonics ; 3D FEM

PDF (3132KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李乐, 董菲, 赵吉文, 苏云升, 盘真保. 基于线圈倾斜方法的永磁同步直线电机推力波动抑制研究. 电气工程学报[J], 2015, 10(8): 45-49 doi:

Li Le. The Study of Reduction of the Thrust Ripple According to Coil Arrangement in PMLSM. Journal of Electrical Engineering[J], 2015, 10(8): 45-49 doi:

1 引言

相比于“旋转电机加同步带”、“滚轴丝杠”等把旋转运动转化成直线运动的装置,直线电机具有大推力、高精度、高加速度且高定位精度等优点,被广泛应用于二维或者三维数控机床。然而,因推力波动产生的噪声、机器振动等因素,限制了直线电机的发展。

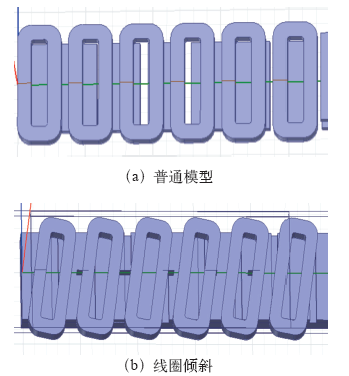
直线电机的推力波动主要由两个因素产生：①电机开槽[1,2]和电机初级和次级的长度有限而产生的定位力[3];②电机反电动势中的高次谐波成分[4]。由于本文的研究对象是一台无铁心永磁同步直线电机,不存在定位力干扰问题,推力波动产生的原因主要由高次谐波引起,所以本文只对反电动势中的高次谐波进行分析。

永磁同步直线电机中的谐波主要是由于永磁体和线圈的排列非正弦,导致气隙中的磁场分布非正弦等现象产生的。抑制谐波干扰的主要方法有采用斜磁[5]、斜槽[6,7,8]、错磁[9]、分数槽[10]或改变永磁体形状、海尔贝克阵列[11,12]及永磁体充磁方式等方法。

线圈倾斜法可以使反电动势更加正弦化,有助于减少空间高次谐波的干扰,本文拟采用该方法,实现对推力波动的抑制。

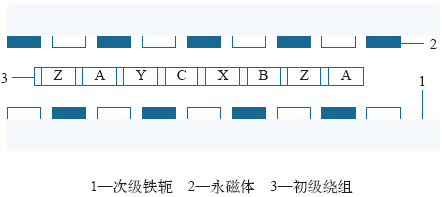
2 永磁同步直线电机的结构

本文以双次级永磁同步直线电机为参照对象,如图1所示,将电机的线圈设计为倾斜结构,线圈采用节距为1的集中式绕组;槽极配合为短初级长次级七极十二槽的分数槽;次级由背铁和永磁体构成,永磁体按照N极、S极交替排列贴在背铁上,上下为N极、S极相对,采用轴向的充磁方式,如图2所示。电机的设计参数见表1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   直线电机参照平台

Fig.1   The machine reference platform


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   双次级永磁同步直线电机示意图

Fig.2   Double-secondary PMLSM structure model


表1   电机的基本参数

Tab.1  The basic dimension of PMLSM

参 数数 值
次级长度/mm605
次级宽度/mm10
次级高度/mm40
永磁体长度/mm40
永磁体宽度/mm3
永磁体高度/mm15
极距τ/mm19
气隙/mm2
极数7

新窗口打开| 下载CSV


3 线圈倾斜对谐波和推力的影响

当线圈倾斜一个角度时,由于同一根导体的各个小段在磁场中的位置互不相同,线圈的有效长度相对减小,电机的推力波动减小的同时,推力也会减小。为了弥补推力的削弱,可以增加永磁体的长度,从而增加磁场强度,加大推力。

倾斜的线圈可以看成由无限多个相邻的微小的直导体串联组成,直导体数为s,s趋于无穷大。每相邻的直导体之间有一个微小的相位差α,而sα = β,β为整个线圈斜过的电弧度。引入一个倾斜因数[13],对推力和谐波的削弱进行定量的分析。

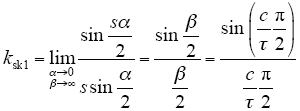
式中,c为x轴方向线圈倾斜的距离;τ为极距;s为直导体数;α为相邻导体之间的夹角。

由式（1）分析知,永磁体长度增加为原来的1/ksk1倍,即可弥补线圈倾斜一个角度所引起的推力削弱的影响。

图3为线圈的分布示意图。其中,图3a为普通的线圈,图3b为倾斜一个角度的线圈,两个模型除了线圈的排列相差一个倾斜角度之外,其他参数都一样。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   线圈分布图

Fig.3   The arrangement of the coil


对于一般的数控机床,推力的峰谷值满足要求的情况下,推力即达到要求。所以在式（2）中,没有计算出每一点的波动,只要计算出峰谷值的波动即可得推力波动为

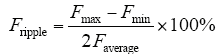
式中,Fmax为推力的峰值;Fmin为推力的谷值;Faverage为推力的平均值。

为了对电机的结果进行谐波分析,以谐波畸变率为指标,对电机的反电动势进行谐波分析。谐波畸变率

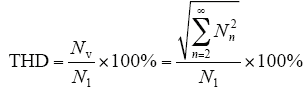
式中,N1表示基波幅值;Nn表示n次谐波幅值。

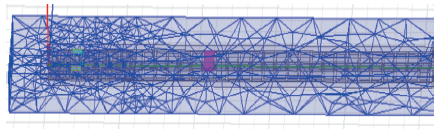
4 有限元仿真

4.1 不同倾斜距离推力和波动分析

根据表1及线圈倾斜结构的变化,分别建立3D有限元模型如图4所示,并进行仿真计算。倾斜距离的变化范围为4mm、8mm、12mm、16mm、19mm、23mm。仿真结果见表2。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   3D有限元仿真模型

Fig.4   3D FEM model


表2   不同倾斜距离推力和波动

Tab.2  The thrust and ripple of different skew length

序号倾斜距离/mm推力均值/N推力波动（%）
1030.119.088 9
2429.688.937 8
3828.278.484 5
41225.857.801 9
51622.696.878 5
61919.375.786 0
72315.195.586 3

新窗口打开| 下载CSV


从图5可以看出,倾斜长度在10~20mm时,随着倾斜角度的增加,平均推力和推力波动都在减小,并且减小的趋势很快。过了20mm的时候,推力较小幅度依然很大,推力波动减小减缓。依照图4,选取倾斜距离为19mm的大小,这个大小正好与永磁同步直线电机的极距相等。此时,虽然推力波动减小,推力也跟着减小,可以采用增加永磁体长度的办法,把永磁体的长度增加为62mm,来弥补线圈倾斜造成的推力的削弱。

图5

新窗口打开| 下载原图ZIP| 生成PPT

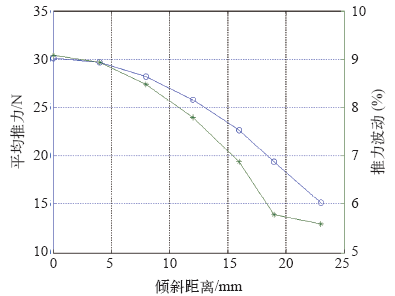
图5   推力和波动与倾斜距离的关系曲线

Fig.5   The relationship of thrust and ripple and skew length


4.2 模型仿真结果与对比

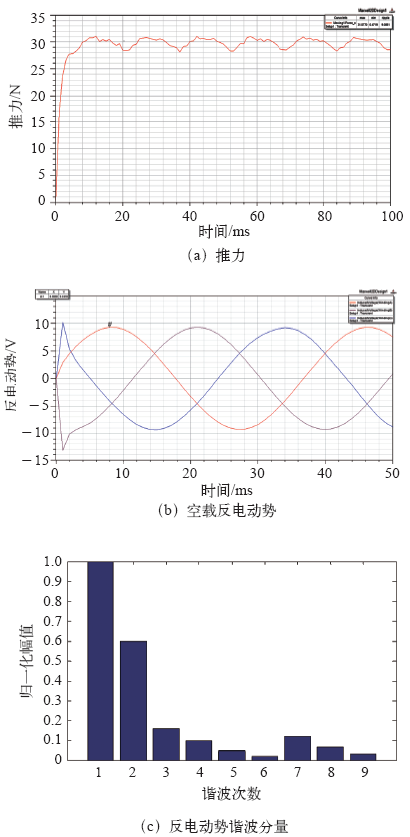
按照表1所列电机参数,建立线圈未倾斜电机的3D仿真模型,得到电机的数据如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   未倾斜时电机推力和反电动势谐波分量

Fig.6   The thrust and harmonics of normal model


线圈没有倾斜时,电机的平均推力为30.11N,推力波动率为9.088 9%,谐波畸变率为64.7%。

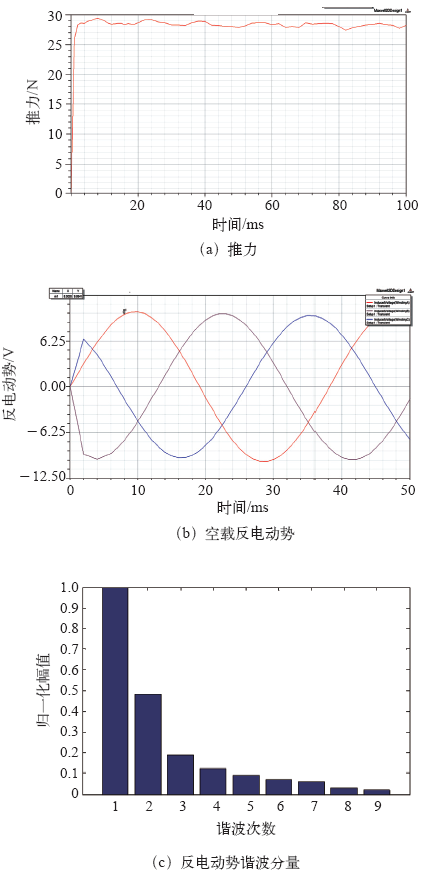
按照表中所列电机参数,建立倾斜一个极距的3D仿真模型,得到电机的数据如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   线圈倾斜电机推力和反电动势谐波分量

Fig.7   The thrust and harmonics of the skew model


当线圈倾斜一个极距的时候,电机的推力波动减小到5.786%,推力减小到19.37N。把永磁体延长到62mm,但是厚度和宽度不改变,这是随着永磁体长度增长,推力增大,同时推力波动也会增加,但是推力波动增加的速度远小于推力增加的速度。最终得到的电机,平均推力为28.34N,推力波动率为6.224 7%,谐波畸变率为55.46%。

在这里,与原来的电机相比,在保持推力满足要求的情况下,采用线圈倾斜一个角度和伸长永磁体的方法,得到一个推力波动大大减小的电机。

5 结论

本文采用了无铁心永磁同步直线电机集中绕组线圈倾斜的方法,来削弱高次谐波,从而达到减小推力波动的目的。仿真结果充分表明：线圈倾斜会减小推力波动,同时也会减小推力的大小,通过选取合适的的倾斜距离,即线圈倾斜一个极距,同时增加永磁体长度,来弥补因线圈倾斜导致的推力削弱。最终得到一个推力不变而推力波动减小的永磁同步直线电机。

参考文献

Zhu Z Q, Howe D .

Instantaneous magnetic field distribution in brushless permanent magnet DC motors, part Ⅲ: effect of stator slotting

[J]. IEEE Transactions on Magnetics, 1993,29(1):143-151.

DOI:10.1109/20.195559      URL     [本文引用: 1]

Zhu Z Q, Wu L J, Xia Z P .

An accurate subdomain model for magnetic field computation in slotted surfacemounted permanent-magnet machines

[J]. IEEE Transactions on Magnetics, 2010,46(4):1100-1115.

DOI:10.1109/TMAG.2009.2038153      URL     [本文引用: 1]

寇宝泉, 张赫, 郭守仑 , 等.

辅助极一体式永磁同步直线电机端部定位力抑制技术

[J]. 电工技术学报, 2015,30(6):107-113.

[本文引用: 1]

Kou Baoquan, Zhang He, Guo Shoulun , et al.

A study of reduction of terminal detent force according to auxiliary pole in PMLSM

[J]. Transactions of China Electrotechnical Society, 2015,30(6):107-113.

[本文引用: 1]

Chung Myung J, Lee Moon G, Lee Sung Q , et al.

A method of optimal design for minimization of force ripple in linear brushless permanent magnet motor

[C]. IEEE Industry Applications Conference, 2000: 36-39.

[本文引用: 1]

Hwang In Cheol, Jang Ki Bong, Kim Gyu Tak .

A study on the characteristics analysis according to overhang and skew of permanent magnet in PMLSM

[C]. Proceeding of International Conference on Electrical Machines and Systems, Seoul, 2007.

[本文引用: 1]

赵海森, 刘晓芳, 罗应立 , 等.

转子斜槽及不同槽斜度对鼠笼式异步电机损耗影响的时步有限元分析

[J]. 中国科学:技术科学, 2011,41(10):1380-1387.

[本文引用: 1]

Zhao Haisen, Liu Xiaofang, Luo Yingli , et al.

Time-stepping FEM of loss in squirrel-caged induction asynchronous motor based on different skewing angels in slot

[J]. Chinese Science: Technical Science, 2011,41(10):1380-1387.

[本文引用: 1]

丁树业, 李跃龙, 李冠男 , 等.

多工况条件下异步电机斜槽与谐波特性

[J]. 沈阳工业大学学报, 2014,36(2):127-132.

[本文引用: 1]

Ding Shuye, Li Yuelong, Li Guannan , et al.

Characteristic of shewing-slot and harmonics of asynchronous motor under the condition of many conditions

[J]. Journal of Shenyang University of Technology, 2014,36(2):127-132.

[本文引用: 1]

乔鸣忠, 张晓锋, 李槐树 .

考虑定子斜槽及转子运动永磁推进电机反电动势及定位力矩的数值计算

[J]. 武汉理工大学学报(交通科学与工程版), 2004,28(5):645-648.

[本文引用: 1]

Qiao Zhongming, Zhang Xiaofeng, Li Huaishu .

Numerical calculation of the driving back EMF and detent force considering stator-skewing and rotor moving

[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering), 2004,28(5):645-648.

[本文引用: 1]

Zhao Jiwen, Liu Kai, Chen Panpan , et al.

Reduction of detent force in permanent magnet linear synchronous motor with double secondary sides

[C]. 17th International Conference on Electrical Machines and Systems, Hangzhou, 2014.

[本文引用: 1]

郭思源, 周理兵, 齐歌 .

双三相永磁同步电机电磁性能解析计算

[J]. 电工技术学报, 2014,29(5):21-27.

[本文引用: 1]

Guo Siyuan, Zhou Libing, Qi Ge .

Analytic calculation of double permanent magnet synchronous motor

[J]. Transactions of China Electrotechnical Society, 2014,29(5):21-27.

[本文引用: 1]

宋玉晶, 张鸣, 朱煜 .

Halbach 永磁阵列磁场解析求解及推力建模

[J]. 电工技术学报, 29(11):62-67.

[本文引用: 1]

Song Yujing, Zhang Ming, Zhu Yu .

Analytical algorithm and thrust modeling based on halbach arrangemet of permanent magnet

[J]. Transactions of China Electrotechnical Society, 29(11):62-67.

[本文引用: 1]

Xia Z, Zhu Z, Howe D .

Analytical magnetic field analysis of halbach magnetized PM machines

[J]. IEEE Transactions on Magnetics, 2001,37(4):2827-2830.

DOI:10.1109/20.951319      URL     [本文引用: 1]

汤蕴璆, 罗应力, 梁艳萍 . 电机学[M]. 北京: 机械工业出版社, 2008.

[本文引用: 1]

/

〈 〉