1 引言
国内外关于电网参数估计的研究方法主要有两种:①基于残差和量测误差之间关系的灵敏度分析,这种基于灵敏度分析的状态估计与参数估计,采用常规的状态变量向量,在状态估计结束后再进行参数估计[5,6];②基于增广矩阵的估计,又可以分为基于常规方程的增广矩阵分析和基于卡尔曼滤波原理的增广矩阵估计两种[7,8,9]。但是,这两种方法均受不良量测的影响,后者同时容易受线路参数误差的影响,估计结果往往不可靠[10],且总存在不收敛的情况。文献[6,11,12]通过采用多个时间断面的采集数据并求取平均值的方法来降低随机的量测误差。文献[10]通过对电网进行分区来避免不同区域间不良数据的影响。但是,这些方法都不能很好地解决量测误差及参数误差影响增广状态估计收敛性及结果可靠性的问题。文献[13]在结论中指出其进行参数估计时需要首先进行参数辨识,辨识的可疑参数集合选择较好时,估计结果较为准确,但该文献只是做出假设并未真正实现。
针对上述情况,本文首先通过历史数据来衡量所选量测的可用性,然后通过对参数的多断面计算结果聚类来辨识可疑参数及定位不良量测,对其修正得到偏差较小的近似值,进而通过增广状态估计提高数据的准确度。这种方法能够改善由于可疑参数存在或不良量测偏差较大而影响其收敛性或结果可靠性的情况。近似值的存在不可避免地会引起残差污染和残差淹没,本文从物理连接、电气连接和功率传输三方面分析并采用博弈论得到电网节点的综合相关度,来降低这种可能,进一步提高结果的准确度。本文结合多代理理论提高计算效率,且各支路AG间可以通信交互[14,15],更好地完成参数辨识、修正及量测的定位、修正,支路AG与CAG反复修正更新,以保证最终结果的可靠性。
2 基于改进聚类的量测数据的处理
2.1 改进最近邻聚类
2.1.1 基于灵敏度的权系数向量的设置
聚类分析在实际应用中,样本向量中不同属性的元素对目标的影响程度也不相同,若忽略此差异,直接利用样本特征值进行聚类,可能导致聚类结果不理想。因此,本文引入灵敏度分析方法,以Di表示样本向量中属性为i的元素,F(D1, D2, ⋯, Dn)表示目标函数,则可通过灵敏度来分析某属性元素对目标函数的影响程度。进而,依据影响程度的大小来设置权系数,以量化不同属性元素对目标函数影响的不同程度。
针对本文线路参数的计算(见3.1),目标函数有R(P, Q, U)、X(P, Q, U)和B(P, Q, U),可采用其均值作为最终目标函数F(P, Q, U),表示为
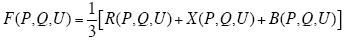
同时,属性为有功功率、无功功率和电压的量测均为首末两端点,采用两端点量测对目标函数灵敏度的均值作为某属性的灵敏度
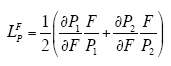
则量测中属性为有功功率的权系数设为
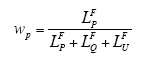
相应地,属性为无功功率和电压幅值的权系数采用相同的方式获取。
根据不同属性设置权系数后,样本向量Xi与向量Xj的相似度可表示为
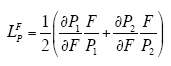
式中,l代表属性;a为属性的种类数;xil、xjl分别为样本向量Xi和Xj中属性为l的元素;wl为样本向量中属性为l的元素的权重。
2.1.2 聚类中心的选取
最近邻聚类算法直接以首个样本作为聚类中心,具有较大的随机性,可能导致聚类结果不均衡。针对这一情况,本文提出了全局相似度的概念,即某样本与所有样本的相似度之和,如式(4)所示。利用全局相似度求取聚类中心,将全局相似度最大的样本向量作为第一个聚类中心,如模型(5)所示,剩余样本集采用同样的方法依次获取聚类中心,直至完成聚类。
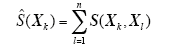
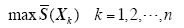
采用这种方法选取聚类中心,避免了聚类中心选取的随机性,能够将与其它样本联系最紧密的样本作为聚类中心,保证了聚类结果的均衡性。
2.1.3 粒计算聚类及阈值的确定
信息粒化的过程是将一类对象划分为一系列的粒,其中每一个粒是基于不可分辨关系、相似性或泛函性聚集而得到的一个对象的集合。粒度指微粒大小的平均度量,从粒度的角度来看,求解的问题不同,则需要的粒度描述也不同,才能得出比较理想的结果。将粒计算理论引入到聚类中,此时聚类以相似度函数作为基础,在所有可能的粒度中找出一个最合适的粒度来分析问题,有效地完成聚类。
聚类的最终数目和类内的样本数均主要取决于阈值。在一般的聚类算法中,采用某一固定阈值进行聚类,可能导致有的类比较密集,而有的类则比较稀疏。为了避免这种情况,本文在同一粒度下进行聚类,并提出了平均相似度的概念,如式(6)所示,每次聚类均以当前剩余样本的平均相似度作为阈值δ。也就是说,当前剩余样本的平均相似度即为本文所选粒度。
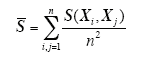
式中,n为剩余样本的样本总数。
2.2 基于改进聚类的量测数据的处理
本文选取某天96个时刻断面的量测对输电线路参数进行计算。为避免所选量测是大规模故障情况下的采集数据,节省重新计算的时间,本文在计算之前对所选量测数据进行粗检。
假设本月共31天,每15min一次采集数据,建立月历史数据库K={X1,X2,…,X2975,X2976},其中,Xi为第i个断面特征向量,包括所有线路两端的有功功率、无功功率和电压。同时,尽量选取与该天相近且天气情况变化不大的某月,因此,历史数据库K中的量测可以作为参考依据对数据进行处理。对K中所有的断面特征向量进行改进聚类处理,假设聚类结果为l类,判断该天96个断面特征向量是否可以归为与其相似度最大的某聚类中心所属类,进而得到可以归类的断面总数,以此来衡量该天量测的可用性,若不可用,需重新选取,再次进行粗检。
3 输电线路可疑参数的辨识
3.1 线路参数的计算
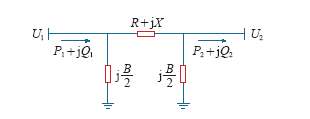
在电力系统计算中,输电线路通常采用Π形等效电路,如图1所示,P1和P2、Q1和Q2以及U1和U2分别为线路两端的有功功率、无功功率以及电压幅值;R、X和B分别表示线路的电阻、电抗和电纳。
图1
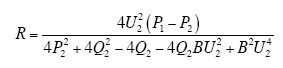
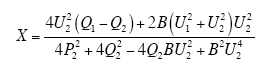
若Q2+Q1≥0,则
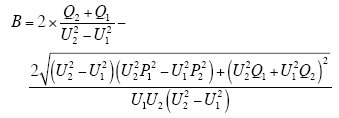
若Q2+Q1<0,则
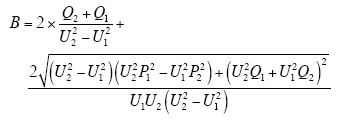
3.2 可疑参数的辨识及不良量测的定位
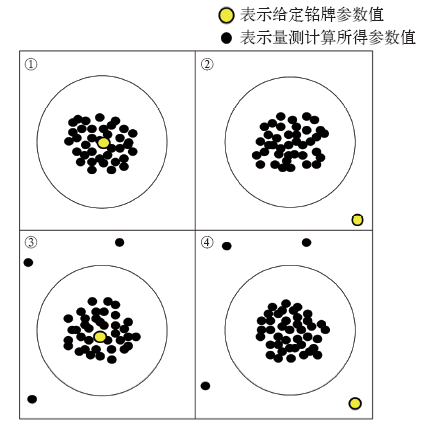
利用可用量测,根据上述线路参数的计算公式,可以得到每条线路相应的96个断面参数值。在实际中,量测数据波动范围很大,虽然由于环境变化或线路老化等原因线路参数也会有所波动,但是线路的参数值会在某一小范围内变化,不会有很大的波动。因此,本文对96个断面参数计算结果进行聚类,以参数正常波动范围设置阈值,来辨识可疑参数同时定位不良量测。
采用经过可用性衡量的量测数据,能够避免数据大规模出错的特殊情况。因此,参数的聚类结果一般可分为四种情况:
(1)量测正确且给定铭牌参数正确:96个断面量测计算所得参数可聚为一类,且给定参数能归到该类。
(2)量测正确且给定铭牌参数可疑:96个断面量测计算所得参数可聚为一类,但给定参数不能归到该类,辨识此线路参数为可疑参数。
(3)部分断面量测错误且给定铭牌参数正确:大部分断面量测计算所得参数可聚为一类,且给定参数能归到该类,部分错误断面量测计算所得参数不能归到该类,由此定位不良量测的时刻及线路编号。
(4)部分断面量测错误且给定铭牌参数可疑:大部分断面量测计算所得参数可聚为一类,但给定参数不能归到该类,辨识此线路参数为可疑参数。部分错误断面量测计算所得参数不能归到该类,由此定位不良量测的时刻及线路编号。
具体情况可通过图2表示。
图2
对上述方法进行分析可知,对于存在可疑参数的情况(2)和(4),该方法能够准确地对可疑参数进行辨识,进而以聚类中心的参数值作为可疑参数的近似参数。对于存在不良量测的情况(3)和(4),该方法也能够准确地对不良量测进行定位,其中包括因缺少个别量测导致参数错误而定位的不良量测。
3.3 不良量测的修正
采用上述方法能够定位不良量测的线路编号及时刻,为得到偏差较小的近似量测,本文采用下述两种方法对不良量测进行修正。
3.3.1 基于节点功率平衡的不良量测的修正
根据KCL定律,在电网中连接在某一节点上的功率是平衡的,即所有正常的有功功率和无功功率分别相加的总和为零
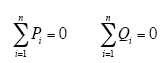
当某节点所连线路中的一条线路的量测出错时,其正确的量测可由其他线路量测根据式(11)得到。对于该线路的电压值,则可由式(12)得到。
3.3.2 基于横纵向的不良量测的修正
对于连接在同一节点的线路中,两条及两条以上线路同时存在不良量测的情况,本文提出一种基于横纵向的不良量测的修正方法。横向是指以月历史数据库中与其处于同一时刻的量测数据为参考依据,纵向是指以该天量测中处于其上一时刻或下一时刻的量测为基准数据。假设不良量测定位到第i条线路的第t时刻,则对其修正的过程如下:
(1)横向:以历史数据库K中的量测为参考依据,来修正该不良量测。
从K中获取线路i对应的31个t时刻及31个t-1时刻的断面特征向量(假设本月共31天),得到St={St,1, St,2, …, St,31}和S(t-1)={S(t-1),1, S(t-1),2, …, S(t-1),31}。将线路i该天t-1时刻的量测分别与S(t-1)中31个量测进行比较,剔除相对差值较大的量测S(t-1), j(假设存在m个,相对差值大于30%),得到一组量测向量S′(t-1)及与其相对应的S′t,进而求取线路i的量测从t-1时刻到t时刻的平均变化率
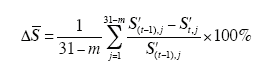
式中,S代表有功功率、无功功率或电压,需要分别求取不同属性量测的平均变化率。
(2)纵向:以t-1时刻的量测作为基准值,利用上述求得的量测平均变化率对基准值进行修正,如式(14)所示,得到量测值 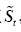
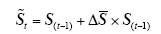
需要说明的是,当不良量测定位到第一个时刻时,用同样的方式,以t+1时刻的量测作为基准值,利用量测从t+1时刻到t时刻的平均变化率对基准值进行修正,得到不良量测的近似量测。
采用这种方法对不良量测进行修正,不仅可以解决某线路单个时刻或多个不连续时刻存在不良量测的问题情况,还可以解决某线路连续多个时刻同时出现不良量测的问题情况。
4 增广状态估计
能量管理系统(EMS)需要准确的线路参数值,尤其是220kV及以上的线路参数,近似参数及近似量测并不能满足要求。而状态估计能在一定程度上提高数据的精度[19],因此本文通过增广状态估计来提高这些参数及量测的精度。与此同时,增广状态估计由于可疑参数存在或不良量测量测偏差较大会导致其不收敛或结果不可靠的问题,利用这些偏差较小的数据来完成增广状态估计,会在一定程度上改善这种情况。
4.1 基于加权最小绝对值的增广状态估计
电力系统增广状态估计的量测方程为
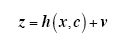
式中,z为m维量测量;x为n维状态量,包括电压幅值和相角;c为参数状态量;v为量测误差;h(x)为m维非线性量测函数矢量,它实质上就是系统的数学模型,表达了量测真值和状态量的相互关系[20]。
加权最小绝对值(WLAV)的估计模型为
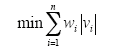
式中,wi为第i个量测分量的权系数;vi为量测误差向量的第i个分量;n为量测个数。
输电线路两端SCADA测量信息中的有功功率、无功功率和电压的量测方程为
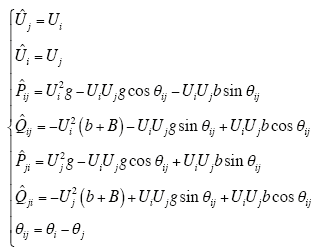
4.2 基于博弈论的电网节点综合相关度的获取
不良量测经修正后得到近似量测,利用这些近似量测直接进行状态估计容易引起残差污染和残差淹没,降低估计结果的准确性。而这种现象一般发生在强相关的节点间[20]。因此,本文从最短距离、节点阻抗和功率传输3个方面来分析电网节点的相关度并采用博弈论得到节点的综合相关度,以此来反映电网节点间发生残差污染和残差淹没的可能。
4.2.1 电网节点相关度的影响因素
本节将从物理连接、电气连接以及实际传输关系三个方面来分析电网节点间的相关度。
(1)最短距离。最短距离是指电网中任意两节点i与节点j之间经历边数最少的一条简单路径所包含的边数和,它反映电网节点之间的物理连接。边数越少,最短距离就越小,而电网两节点间的相关度就越大。
(2)电气耦合连接度。电气耦合连接度是通过电网中任意两节点i与节点j之间的电气距离的倒数来表征的。它反映的是电网节点之间的电气连接,电气耦合连接度越大,则电网两节点间的相关度就越大。
(3)功率传输。功率传输反映电网节点之间的实际传输关系,可由复功率追踪求取。电网两节点间的传输功率越大,表明两节点之间的连接就越紧密,因而两节点间的相关度也就越大。
4.2.2 基于博弈论的电网节点综合相关度的获取
以上3个因素均能从不同方面反映电网节点的相关度,为了避免片面性,本文采用博弈论获取电网节点的综合相关度。
对于节点i,每种影响因素给出相应的一个向量,以反映该节点与其他节点的相关度,则3种因素得到3个向量,构造成一个基本向量集u={u1, u2, u3},这3个向量任意线性组合构成向量集 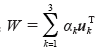
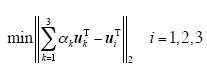
根据矩阵的微分性质,该模型最优化的一阶导
数条件为 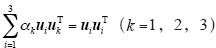
对应线性方程为
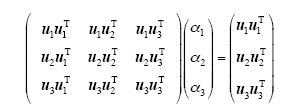
通过计算求得(α1,α2,α3),进行归一化处理后得到 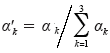
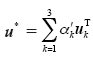
从矩阵U*nn中,可以得到近似数据所在节点与电网其他节点的综合相关度。观察是否存在与其相关度较大的节点(不包含近似数据所在节点),若不存在,直接进行增广状态估计,若存在,本文通过分区来隔离与其相关度较大的节点,避免由于残差淹没或残差污染而降低估计结果的准确度。首先在安全区域内进行部分增广状态估计,进而以其估计值代替近似值完成增广状态估计,提高结果的准确度。
针对多断面增广状态估计的结果,每个断面均得到一组较准确的线路参数,对某线路多断面参数值进行聚类,将聚类中心的参数值作为最终结果,进一步获取准确度更高的参数值。
5 线路参数多代理辨识与估计
对于代理,至今尚没有一个被广泛接受的定义,不同的学科、不同的应用领域,对AG有着不同的定义。Lane在普遍意义上给出了AG的定义:智能体是一个具有控制问题求解机理的计算单元,它可以是一个机器人、一个专家系统、一个过程、一个计算模块或一个求解单元等[24]。
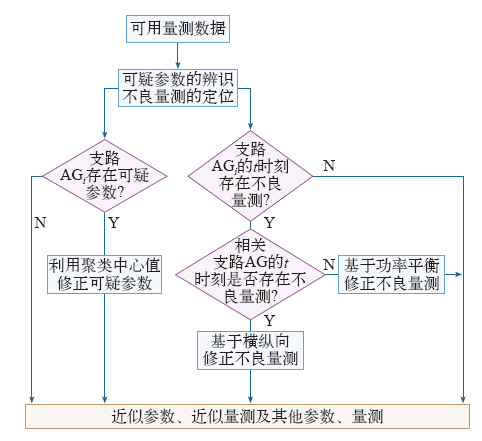
多代理系统通过将复杂问题分解,并交由基本组成单元AG实现,AG具有独立完成任务及与其他AG通信以共同实现复杂系统目标的能力[15]。针对输电线路的独立性和相关性,本文结合多代理理论实现线路参数的辨识与估计,将每条线路作为一个AG,即支路AG,自身实现的功能是线路参数的辨识、修正和不良量测的定位,发挥代理的独立性。同时,各支路AG并行计算,以提高计算效率。每个支路AG除与CAG存在联系外,还和与其处于电网同一节点的相关支路AG进行交互通信,共同完成不良量测的修正,发挥代理的协作性。CAG实现的功能是增广状态估计及多断面处理。各支路AG将经修正得到的近似值及其他数据发送给CAG,由CAG通过增广状态估计得到协调值。然后,再与支路AG通信,将协调值发送给支路AG,重新进行可疑参数辨识及不良量测定位,观察是否仍然存在可疑参数或不良量测,反复协调修正,直至不再存在可疑参数或不良量测,以保证结果的可靠性。此时,CAG将这组数据进行多断面处理,作为最终结果。
各支路AG实现自身功能及与相关支路AG交互的具体过程如图3所示。
图3
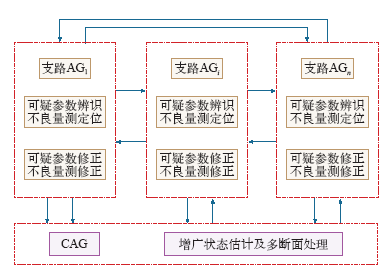
输电线路参数的辨识与估计由各支路AG和CAG分工合作完成,具体的实现模型如图4所示。
图4
图4
线路参数辨识与估计的多代理模型
Fig.4
The multi-agent model of branch parameters identification and estimation
6 仿真分析
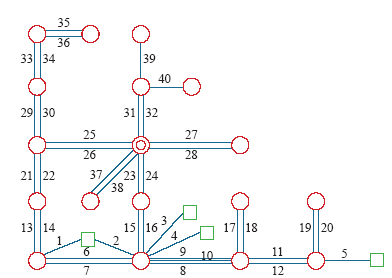
本文以我国某中等城市的实际输电网为例,运用本文所述方法对输电线路参数进行辨识与估计。图5给出了该城市电网系统的站外接线图(图中方框表示电源节点,单圆圈表示220kV厂站节点,双圆圈表示500kV厂站节点)。
图5
6.1 基于改进聚类的量测数据的处理
建立月历史量测数据库,包括31天2 976个时刻的量测,每个时刻断面均包括电网所有线路两端的有功功率、无功功率和电压。采用本文改进聚类的方法对这些数据进行处理,以衡量所选该天数据的可用性。基于改进聚类的数据处理结果以及该天量测的归属情况,见表1。
表1 月数据聚类结果及该天数据归属情况
Tab.1
| 粒计算 聚类结果 | 聚类 中心 | 月样本 断面数 | 与聚类中心最相 似的断面数 | 可归类的 断面数 |
|---|---|---|---|---|
| 1 | 1 198 | 216 | 8 | 7 |
| 2 | 1 618 | 192 | 6 | 6 |
| 3 | 1 761 | 173 | 5 | 5 |
| 4 | 1 323 | 156 | 4 | 3 |
| 5 | 1 016 | 161 | 5 | 5 |
| 6 | 2 420 | 196 | 6 | 5 |
| 7 | 1 777 | 177 | 5 | 4 |
| 8 | 1 429 | 138 | 4 | 3 |
| 9 | 521 | 136 | 4 | 4 |
| 10 | 2 178 | 145 | 4 | 4 |
| 11 | 862 | 156 | 6 | 5 |
| 12 | 697 | 139 | 3 | 3 |
| 13 | 1 588 | 124 | 5 | 5 |
| 14 | 2 366 | 144 | 6 | 5 |
| 15 | 1 806 | 104 | 4 | 4 |
| 16 | 473 | 122 | 4 | 4 |
| 17 | 1 835 | 96 | 3 | 3 |
| 18 | 2 622 | 118 | 4 | 4 |
| 19 | 1 478 | 86 | 3 | 3 |
| 20 | 2 059 | 104 | 4 | 3 |
| 21 | 406 | 72 | 3 | 2 |
| 22 | 1 158 | 21 | — | — |
| 合计 | 可以归类的断面总数 | 87 | ||
由表1可知,该天量测的96个断面中,共有87个断面能够进行归类,超过了70%,说明该天量测不是大规模故障情况下的采集数据,可以用于输电线路参数的辨识与估计。
6.2 可疑参数的辨识和不良量测的定位
为了便于分析,本文根据线路的实际型号和长度,得出各线路的具体参数值,以此参数值直接进行对比分析。在40条线路中选出4条线路,将这些线路的某些参数在真实值的基础上加入不同误差,作为给定铭牌值,进行分析计算。其他线路直接利用参数真实值作为给定铭牌值,加入误差的线路参数情况见表2。
表2 加入误差的线路参数情况
Tab.2
| 线路编号 | 参数真值 | 给定铭牌值 | |
|---|---|---|---|
| 3 | X/Ω | 4.506 5 | 4.218 1 |
| 19 | R/Ω | 0.568 5 | 0.877 3 |
| X/Ω | 3.252 1 | 3.489 2 | |
| 28 | R/Ω | 0.698 4 | 0.498 1 |
| X/Ω | 4.939 7 | 5.153 3 | |
| B/(10-4S) | 0.830 1 | 3.213 | |
| 34 | X/Ω | 10.255 4 | 10.049 1 |
| B/(10-4S) | 1.688 5 | 4.357 4 | |
利用可用量测数据,各支路AG同时对线路参数进行计算,然后对多断面计算结果聚类。根据该城市当天的环境温度及用电等具体情况,来考虑线路参数的大致波动范围,电阻、电抗和电纳分别为0.14Ω、0.15Ω和2.1×10-4S,以此作为参数多断面结果聚类的阈值。由于线路较多,不再赘述,其中辨识结果中存在可疑参数的线路具体情况,见表3。
从表3的辨识结果可以看出,本文方法能够对线路的可疑参数进行准确的辨识,线路3的电抗X为可疑参数,线路19的电阻R和电抗X为可疑参数,线路28的电阻R、电抗X和电纳B均可疑参数,线路34的电抗X和电纳B为可疑参数。
表3给出了参数聚类的聚类中心参数值以及中心参数值与真实值的相对误差,可以看出其偏差不大,将其作为可疑参数的近似参数。进而,通过CAG中的增广状态估计来提高参数的准确度。同时,利用这些偏差较小的近似参数代替可疑参数进行增广状态估计来改善其收敛性及结果的可靠性。
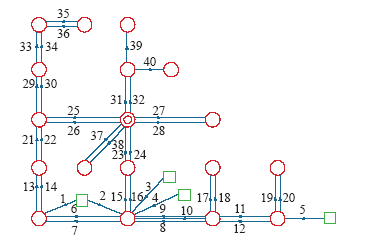
与此同时,采用上述聚类多断面计算结果的方法,还能够定位不良量测的具体时刻及位置,定位结果如图6所示。
由图6能够看出,线路2的5时刻和21时刻、线路3的35时刻和36时刻、线路4的90时刻,线路5的69时刻、线路9的21时刻…线路38的34时刻和75时刻及线路39的34时刻存在不良量测,由此可见,这种方法能够定位到不良量测的具体线路编号及时刻,便于对不良量测进行修正,得到偏差较小的近似量测。
6.3 不良量测的修正
各支路AG自身及其相关支路AG共同完成不良量测的修正,不良量测较多,其中部分不良量测的修正结果见表4。
表4 各支路AG不良量测的修正结果
Tab.4
| 线路 编号 | 时刻 | 相关 支路AG 存在错误 | P1/MW | Q1/Mvar | U1/kV |
|---|---|---|---|---|---|
| P2/MW | Q2/Mvar | U2/kV | |||
| 2 | 5 | 否 | 160.496 215 | 8.010 114 | 223.49 |
| 160.172 338 | 7.989 906 | 223.25 | |||
| 2 | 21 | 否 | 174.674 944 | 37.981 527 | 223.08 |
| 174.273 315 | 37.216 937 | 223.29 | |||
| 3 | 35 | 否 | 242.512 257 | 17.581 242 | 226.71 |
| 241.794 054 | 15.729 693 | 225.71 | |||
| 3 | 36 | 是 | 242.512 249 | 17.581 221 | 226.71 |
| 241.794 011 | 15.729 687 | 225.71 | |||
| 4 | 90 | 是 | 257.001 90 | 0.470 337 | 226.74 |
| 255.988 63 | 2.831 57 | 225.88 | |||
| 5 | 69 | 是 | 256.430 10 | 24.380 611 | 225.77 |
| 256.277 94 | 24.648 329 | 225.72 | |||
| 9 | 21 | 是 | 26.479 221 | 26.011 186 | 223.05 |
| 26.458 972 | 29.149 092 | 222.92 | |||
| 10 | 90 | 是 | 7.0274 55 | 31.011 706 | 223.79 |
| 7.018 997 | 33.867 914 | 223.35 | |||
| 10 | 21 | 是 | 30.344 966 | 35.484 401 | 223.29 |
| 30.327 471 | 37.888 235 | 222.72 | |||
| 14 | 59 | 否 | 134.554 124 | 4.400 775 | 223.76 |
| 134.371 277 | 3.993 922 | 223.52 | |||
| 15 | 36 | 否 | 87.137 219 | 58.004 137 | 227.84 |
| 87.052 143 | 54.997 688 | 225.51 | |||
| 17 | 90 | 是 | 29.198 704 | 16.648 655 | 223.37 |
| 29.184 702 | 19.829 521 | 223.32 |
表4第2列“相关支路AG存在错误”中,“否”代表由其相关支路AG通过通信交互完成不良量测的修正,“是”代表支路AG自身采用横纵向法完成不良量测的修正。由此可知,支路AG自身及其相关支路AG相结合能够实现对各种情况下不良量测的修正,得到偏差较小的近似量测。同样,需要通过CAG中的增广状态估计来提高量测的精度。同时,利用这些偏差较小的近似量测代替不良量测进行增广状态估计来改善其收敛性及结果的可靠性。
6.4 增广状态估计
上述所得近似值并不能满足EMS的需求,各支路AG得到近似参数、近似量测以及其他参数和量测后,将这些数据传送给CAG,由CAG通过增广状态估计提高数据的精度。与此同时,为了降低发生残差污染和残差淹没的可能,首先分区隔离与近似数据综合相关度较大的节点数据,即综合相关度大于0.6的节点,在安全区域内进行增广状态估计。然后,以其估计值代替近似值完成整体的增广状态估计,本文以第36个断面为例进行详细说明,断面36如附录所示。
表5 节点相关度
Tab.5
| 节点 | 与其综合相关度大于0.6的节点 |
|---|---|
| 3-1 | 7-2 |
| 3-2 | 7-2、2-1 |
| 15-1 | 4-1、2-1、7-2 |
| 15-2 | 4-1、23-1 |
注:节点表示方式不唯一。
6.5 3种方法收敛性及结果可靠性的对比
表7 3种方法的收敛性对比
Tab.7
| 方法 | 迭代次数 |
|---|---|
| Ⅰ | 14 |
| Ⅱ | 7 |
| Ⅲ | 5 |
为了更清楚地进行对比,表7中的迭代次数均为各支路AG首次将近似值传送给CAG后,增广状态估计的迭代次数。很显然,本文方法在收敛性方面最好。从方法Ⅰ和方法Ⅱ的对比,可以看出,本文对可疑参数辨识、修正及不良量测定位、修正,以获取偏差较小的近似值来完成参数估计,能够很好地改善增广状态估计的收敛性。方法Ⅱ和方法Ⅲ相比,收敛性也有所改善,但迭代次数变化不大。
表8 3种方法参数估计结果的可靠性对比
Tab.8
| 方法 | 线路3 | 线路28 | ||
|---|---|---|---|---|
| X/Ω | 相对误差(%) | R/Ω | 相对误差(%) | |
| Ⅰ | 4.483 427 | 0.512 | 0.673 677 | 3.54 |
| Ⅱ | 4.503 122 | 0.075 | 0.687 016 | 1.63 |
| Ⅲ | 4.504 247 | 0.05 | 0.691 276 | 1.02 |
| 方法 | 线路28 | |||
| X/Ω | 相对误差(%) | B/(10–4S) | 相对误差(%) | |
| Ⅰ | 4.928 684 | 0.223 | 0.829 119 | 0.118 2 |
| Ⅱ | 4.935 847 | 0.078 | 0.829 743 | 0.043 |
| Ⅲ | 4.937 283 | 0.049 | 0.829 876 | 0.027 |
| 方法 | 线路19 | |||
| R/Ω | 相对误差(%) | X/Ω | 相对误差(%) | |
| Ⅰ | 0.557 357 | 1.96 | 3.235 124 | 0.522 |
| Ⅱ | 0.560 257 | 1.45 | 3.249 596 | 0.077 |
| Ⅲ | 0.574 867 | 1.12 | 3.254 051 | 0.06 |
| 方法 | 线路34 | |||
| X/Ω | 相对误差(%) | B/(10–4S) | 相对误差(%) | |
| Ⅰ | 10.244 320 | 0.108 | 1.685 714 | 0.165 |
| Ⅱ | 10.249 961 | 0.053 | 1.688 061 | 0.027 |
| Ⅲ | 10.251 302 | 0.04 | 1.688 162 | 0.02 |
由表8可以看出,本文方法的参数估计结果准确度最高,即结果最可靠。通过方法Ⅰ和方法Ⅱ的对比,可以看出,方法Ⅰ直接利用未修正的量测及参数进行增广状态估计,不良量测及可疑参数的存在,使得参数估计结果误差较大。而加入可疑参数辨识、修正及不良量测定位、修正后的方法Ⅱ,结果准确度得到了明显的提高。从方法Ⅱ到方法Ⅲ,线路28估计结果准确度提高较多,线路3次之,线路19和线路34提高较少。从方法Ⅱ和方法Ⅲ的区别分析,可知这直接受线路两端节点与近似数据所在节点相关度的大小影响。由此说明,本文以电网节点的综合相关度为依据来降低残差污染和残差淹没的有效性,进一步提高了参数估计结果的准确度。
7 结论
通过理论研究和仿真分析,得到以下结论:
(1)对输电线路参数的多断面计算结果聚类能够准确的辨识可疑参数且定位不良量测。
(2)利用偏差较小的近似值来完成增广状态估计,其收敛性及结果的可靠性均得到了明显的改善。
(3)通过获取电网节点的综合相关度,降低了增广状态估计发生残差污染和残差淹没的可能,进一步提高了估计结果的准确度。
(4)结合多代理理论,各支路AG并行计算,提高了计算效率,同时支路AG与CAG反复修正,则更好地保证了最终结果的可靠性。
本文方法适用于电网结构不变化的情况,对于电网结构发生变化的情况还需进一步研究。
附 录
附图
参考文献
基于故障数据的线路分布参数时域辨识方法
[J].
Distributed parameter time domain identification method of transmission lines based on fault records
[J].
基于主导与非主导参数的非线性加权最小绝对值参数估计
[J].
Nonlinear weighted absolute least value parameter estimation based on dominant and non-dominant parameter
[J].
基于多时段同步测量信息的T接线路参数在线测量
[J].
Online measurement of T-connection transmission line parameters based on multi-Interval synchronized measurement information
[J].
基于在线核学习的电网不良数据检测与辨识方法
[J].
Power grid bad-data detection and identification based on online Kernel learning method
[J].
Estimation of parameter errors from measurement residuals in state estimation
[J].
基于WAMS/SCADA混合量测的电网参数辨识与估计
[J].
Network parameter identification and estimation based on hybrid measurement of WAMS/SCADA
[J].
基于状态估计的电网支路参数估计方法
[J].正确的电网参数是电网安全稳定预警和控制决策的必要基础,研究实用的电网支路参数的估计方法具有重要的现实意义。扩展状态估计法是一种有代表性的参数估计方法,在该算法的实际应用中,发现支路参数不可估计或者估计结果不合理的现象时有发生。该文以IEEE 9系统和中国某实际电网为算例,对扩展状态估计法的性能进行深入研究,找到该方法存在的数值稳定性和局部最优性问题。继而提出一种基于Tabu搜索策略的参数估计方法,经IEEE9标准系统和实际电网算例验证,具有良好的数值稳定性和全局寻优能力,在实际电网得到在线应用。
State estimation based branch parameter estimation method for power grid
[J].正确的电网参数是电网安全稳定预警和控制决策的必要基础,研究实用的电网支路参数的估计方法具有重要的现实意义。扩展状态估计法是一种有代表性的参数估计方法,在该算法的实际应用中,发现支路参数不可估计或者估计结果不合理的现象时有发生。该文以IEEE 9系统和中国某实际电网为算例,对扩展状态估计法的性能进行深入研究,找到该方法存在的数值稳定性和局部最优性问题。继而提出一种基于Tabu搜索策略的参数估计方法,经IEEE9标准系统和实际电网算例验证,具有良好的数值稳定性和全局寻优能力,在实际电网得到在线应用。
Parameter error identification and estimation in power system state estimation
[J].
卡尔曼滤波理论在电力系统中的应用综述
[J].
A survey on the application of Kalman filtering method in power system
[J].
基于权函数的电网参数分区辨识与估计方法
[J].
Yujuan, et al. A divisional identification and estimation method of network parameter errors based on weight function
[J].
基于多方式断面的输电网络参数估计
[J].
Parameter estimation of power transmission network based on multi-cases of power flow operating conditions
[J].
基于PMU及多时间断面的输电网参数估计
[J].
Parameter estimation based on PMU and multi-cases of SCADA for electricity transmission network
[J].
基于线性内点法及正交变换的抗差参数估计
[J].
WLAV robust parameter estimation based on linear interior point algorithm and orthogonal transformation
[J].
含分布式电源的配电网多故障抢修的多代理策略研究
[J].
Multi-agent strategy of distribution networks multi-faults rush-repair with distributed generators
[J].
采用多代理技术提高高压配电网的供电可靠性
[J].
Application of multi-agent technology to enhance power supply reliability of high voltage distribution network
[J].
Pattern classification with granular computing
[C].
Research and progress of cluster algorithms based on granular computing
[J].
基于粒计算的概念聚类算法
[J].
Conceptual clustering algorithm based on granular computing
[J].
基于权函数的电力系统状态估计算法
[J].
Weight function based power system state estimation algorithm
[J].
基于复杂网络理论的大电网结构脆弱性分析
[J].
Structural vulnerability analysis of large power grid based on complex network theory
[J].
支路复功率损耗和潮流分量的归属分析
[J].
Analysis on attribution of branch complex power loss and complex power flow component
[J].
基于博弈论的综合赋权法的信息安全风险评估
[J].
A comprehensive weight method based on the game theory for information security risk assessment
[J].
Distributes problem solving and real-time mechanism in robot architecture
[J].