1 引言
高频开关谐波是PWM整流器的必然产物,特别是对于有源电力滤波器[1,2,3](Active Power Filter,APF)来说,应该避免高频谐波造成电网的二次污染。此时,通常在装置并网侧安装低通滤波器(Low Pass Filter,LPF)[4]。该方法需要同时兼顾APF最高次谐波的补偿效果和最低次高频开关谐波的抑制效果,往往不能完全消除高频谐波,且当APF为了满足某些领域的大容量补偿要求而采用模块化并联结构[5,6]时,总体输出高频谐波就比较明显,而在并联系统总输出安装LPF时,设计容量较大,且无功容量难以满足设计要求。为此,人们将载波相移SPWM(Carrier Phase-Shifted SPWM,CPS-SPWM)技术引入到并联系统控制中来[7,8,9],该调制策略具有等效开关频率高、输出谐波含量小以及控制方法简单等优良特性,能够通过提高谐波频率来抑制系统输出高频谐波,降低LPF的设计容量和难度。
文章研究基于对称规则采样方法的多模块APF并联系统的谐波特性,旨在为并联系统的LPF参数选择、各模块的协调控制、并联环流的形成机理分析以及保护等提供理论指导。文章首先对基于对称规则采样法的单个APF模块的SPWM输出电压、电流的谐波特性进行了分析,在此基础上,通过建立并联系统的数学模型,分析了基于CPS-SPWM的APF并联系统的谐波特性。最后,对上述理论进行了实验验证。
2 基于对称规则采样法的三相并联型APF SPWM谐波特性分析
2.1 三相并联型APF系统结构及其数学模型
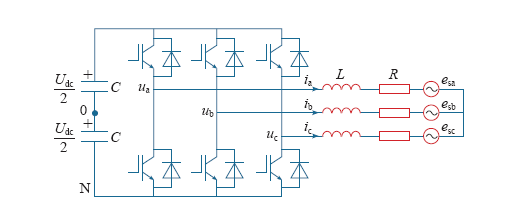
三相并联型APF系统电路模型如图1所示。
图1
图中,L、R分别为网侧连接电抗和等效电阻,C为直流滤波电容;Udc为直流侧电压;ix、ux、esx分别为APF补偿电流、相电压和电网电压,x=a, b, c。文章为了特出对交流谐波特性的分析,取电压参考点为直流电压中心点0,以避免选择参考点N所带来的直流分量,而两种参考点下输出电压交流谐波特性一致。
为了简化分析,设电网三相电压对称无畸变,并忽略网侧等效电阻。此外,由于APF补偿n(≥2)次谐波电流,文章根据线性叠加原理,仅对任一单次谐波进行分析。
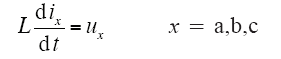
鉴于装置的三相对称性,下面均以a相为例分析问题。
2.2 输出电压谐波特性分析
2.2.1 基于载波频率的输出电压函数
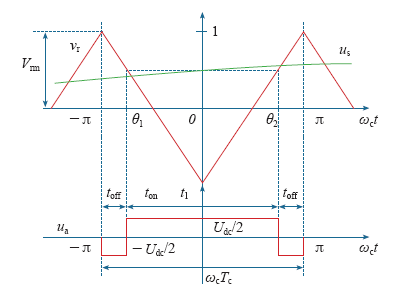
图2为基于对称规则采样法的一个载波周期Tc中SPWM输出电压局部放大图。图中,Vrm为载波峰值,us为正弦调制波,在t1时刻采样us,并用采样数值与载波相比较来生成触发脉冲,ton时区触发桥臂上管导通、下管关闭,toff时区触发桥臂下管导通、上管关闭,可见该触发脉冲在Tc中呈对称分布。
图2
图2
基于对称规则采样法的APF单相输出电压
Fig.2
The single-phase output voltage of the APF based on irregular sampling
设正弦调制波函数us为
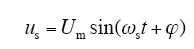
式中,Um、ωs和φ分布为调制波的幅值、角频率和初相角,令调制比M=Um/Vrm。
本文以载波角频率ωc为基准来分析ua的谐波特性。图中,θ1、θ2为一个载波周期2π中ua生成的触发边沿时刻。
结合图2和式(2),求得θ1、θ2的取值
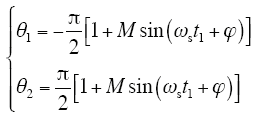
则ua一个载波周期的表达式为
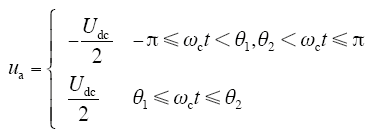
将ua展开成Fourier级数的形式,并令t=t1,具体过程略。即
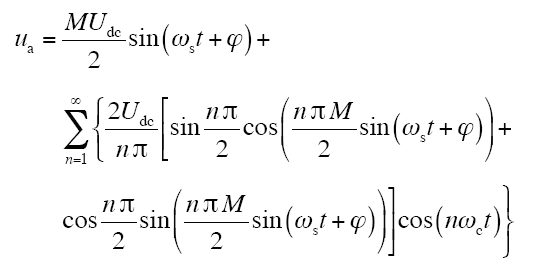
观察式(5),当n为偶数时,sin [(nπ)/2]=0;而当n为奇数时,cos [(nπ)/2]=0,因此,可将式(5)进一步化简为
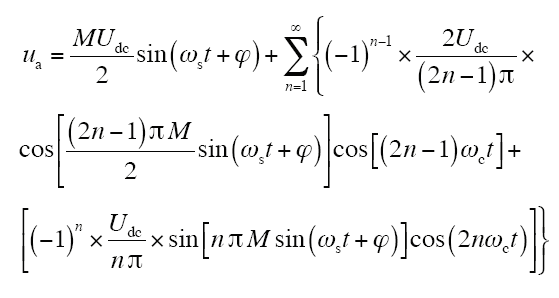
2.2.2 ua的谐波特性分析
由式(6)可见,ua由两个部分组成,这里分别记为uas和uan,其中
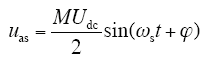
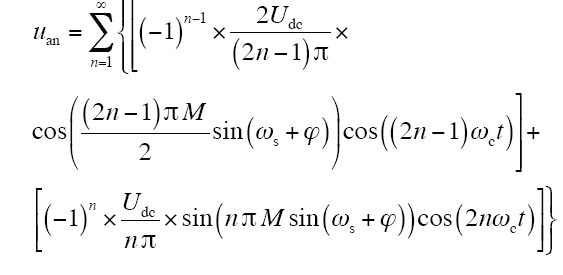
式中,uas其与载波无关,仅与调制波us和调制系数M相关,这里称之为低频调制分量。可见,低频调制分量uas与us同步,其幅值等于MUdc/2,与调制系数M成正比。
uan为与ωc相关的高频谐波,这里称为高频开关分量。下面将重点分析uan的高频谐波特性。
为了深入研究uan的谐波特性,引入贝塞尔函数[12]
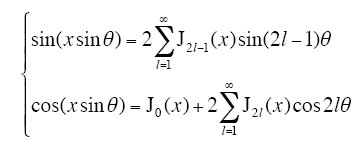
利用贝塞尔函数将式(8)中的项sin[nπMsin(ωst+φ)] 、 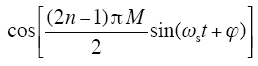
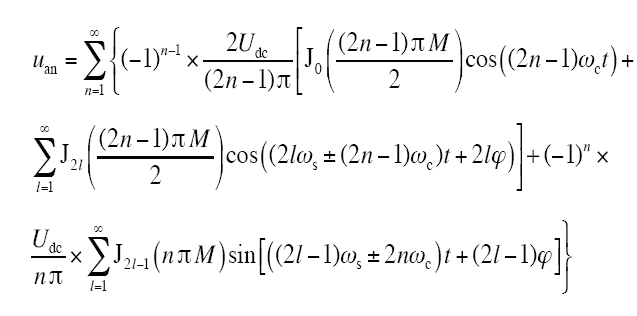
分析式(10),uan的谐波分布由两部分组成:
(1)谐波频率为(2n-1)ωc±2lωs,谐波分布在奇数倍载波频率(2n-1)ωc附近,且由于其边频为偶数次调制波频率,即2lωs,因此谐波呈奇数次分布;谐波幅值为 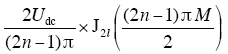
2, …,l=0, 1, 2, …。
(2)谐波频率为2nωc±(l-1)ωs,谐波主要分布在偶数倍载波频率2nωc附近,且由于其边频为奇数次调制波频率,即(2l-1)ωs,谐波呈奇数次分布;谐波幅值为 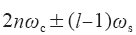
综合分析可知,高频谐波uan分布在n倍的载波频率即nωc附近,且呈奇数次分布,n=1, 2, …。
2.3 输出电流谐波特性分析
参照第2.2.2节,定义ia的低频调制分量和高频开关分量分别为ias和ian。
2.3.1 低频调制分量ias
根据式(1)和式(7),并令ua初始值为0(下同),求得ias(过程略)
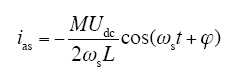
分析式(11),ias的幅相特性为
(1)相频特性:滞后uas相位角度为π/2,这是由电感特性决定,参照式(1),下同。
(2)幅频特性:相比较于电压uas,幅值提高1/(ωsL)倍,且在L既定情况下,与ωs成反比。
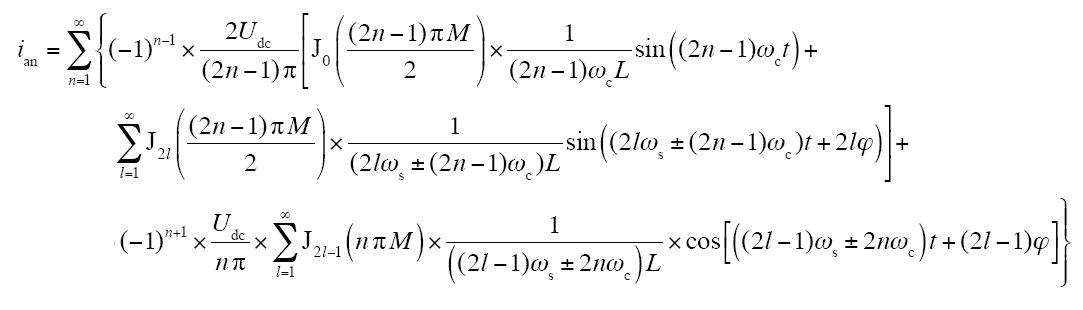
2.3.2 高频开关分量ian
结合式(1)和式(10),可求得ian
由(12)可见,ian具有以下谐波特性:
(1)谐波分布特性。类似于uan的谐波分布,高频开关谐波ian分布在n倍的载波频率即nωc附近,且呈奇数次分布,n=1, 2, …。
(2)幅值特性。由于通常情况下ωcL>1,且 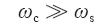
3 基于CPS-SPWM的APF并联系统谐波特性分析
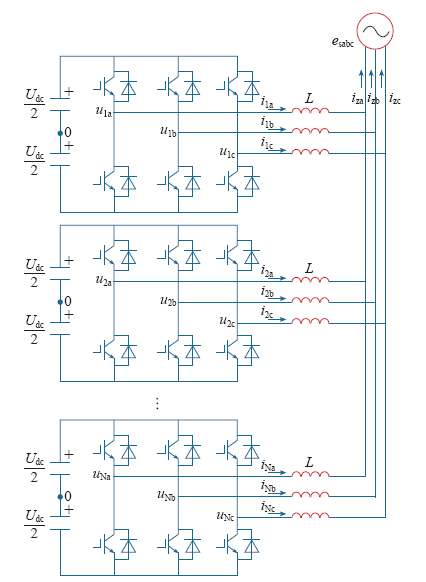
3.1 并联系统结构及其数学模型
图3
装置采用基于CPS-SPWM的开关调制方法,各单元载波相互错开时间Ts=Tc/N,即载波相位依次滞后2π/N。为了简化分析,在2.1节单个APF模块基础上,对并联系统作如下特征设定:各模块元件参数一致,直流侧电压相同;各模块具有相同的调制波函数us。
根据图3及上述并联系统特征,将各模块形如式(1)的数学模型表达式求和,即
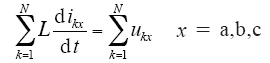
由图3,根据基尔霍夫电流定律可得 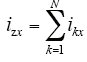
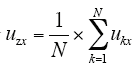
式(13)可得并联系统谐波数学模型
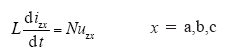
3.2 并联系统谐波特性分析
下面仍然以a相为例分析问题,根据式(14),文章首先分析uza的谐波特性,在此基础上,分析并联系统输出总电流iza的谐波特性。
3.2.1 uza的谐波特性
参照第2.2.2节,定义uza的低频调制分量和高频开关分量分别为uzas、uzan,按照3.1节并联系统特征,并结合式(7)~式(10),分析uza的谐波特性。
(1)低频调制分量
由式(7)可知,各模块低频调制分量ukas相同(k=1, 2, …, N),因此有
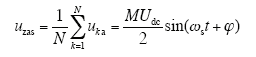
可见,uza与各模块输出电压uka的低频调制相同,k=1, 2, …, N。
(2)高频开关分量
由式(8),可得各并联模块输出电压谐波分量
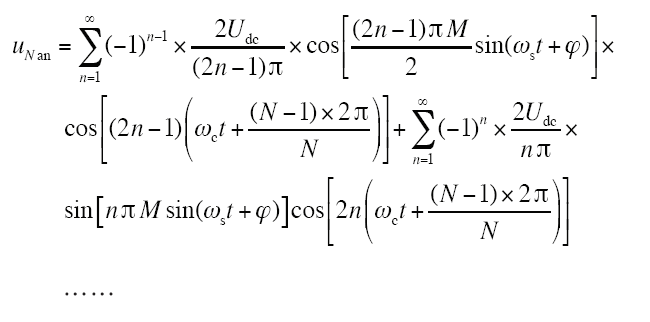
对于和式
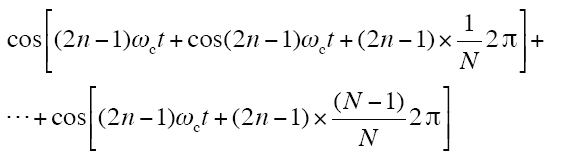
仔细分析可知,只有当2n–1等于整数倍的N时,和式等于Ncos((2n–1)ωct),而当2n–1取其他值时,和式为0;另一方面,由于2n–1为奇数,只有当N亦为奇数时两者才可能存在整数倍关系,且该倍为数奇数,因此,取2n–1=(2m–1)×(2N–1),m=1, 2, 3, …。
同理,对于和式
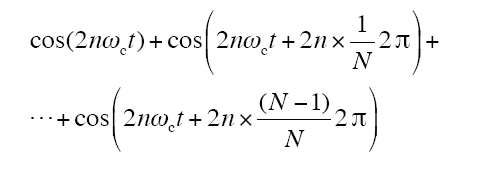
只有当2n等于整数倍的N时,和式等于Ncos (2nωct),其他取值时,和式为0;同时,当N取偶数时,为连续整数倍关系,此时,取2n=m×2N,m=1, 2, 3, …;当N取奇数时,为偶数整数倍关系,此时取2n=2m×(2N-1),m=1, 2, 3, …。
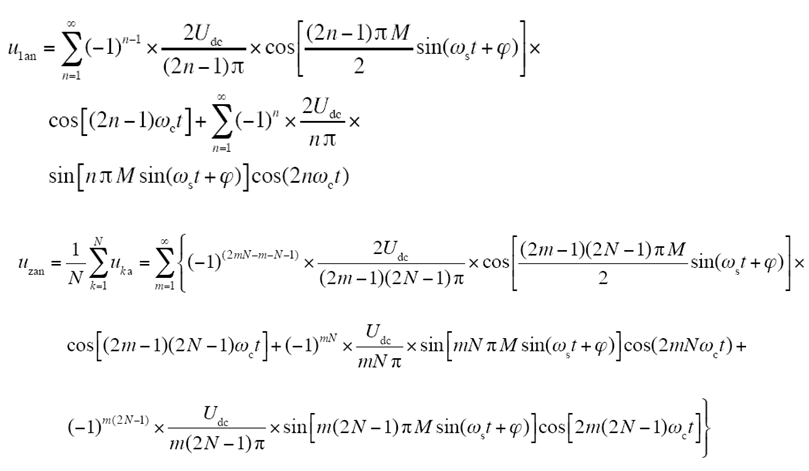
根据上述关系,可求得高频谐波分量uzan
同理,可以利用式(9)的贝塞尔函数分析式(16),可解得式(17)。
根据式(17),可得出uzan的以下高频谐波特性,具体谐波分布包括3个部分:
(1)谐波频率为(2m-1)(2N-1)ωc±2lωs,谐波分布在(2m-1)(2N-1)倍的载波频率ωc附近,且其边频为偶数次调制波频率,即2lωs,谐波呈奇数次分布;谐波幅值为 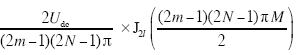
式中,m=1, 2, 3, …;l=0, 1, 3, 5, …。
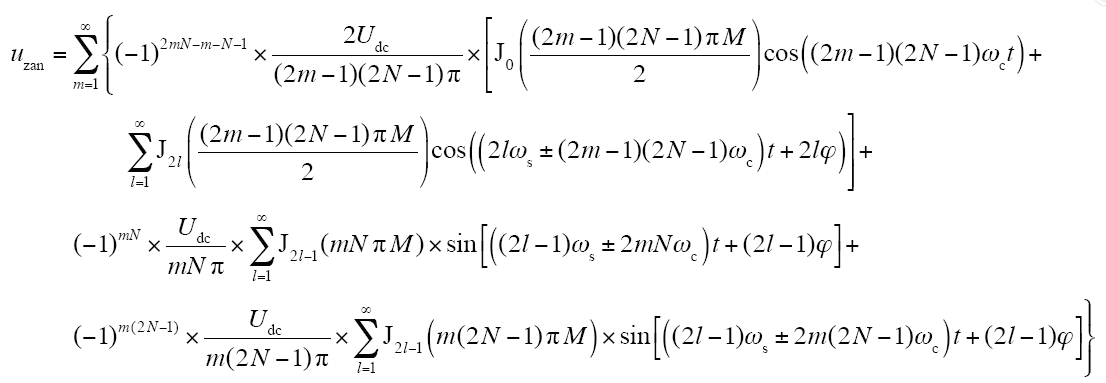
(2)谐波频率为2mNωc±(2l-1)ωs,谐波分布在2mN倍的ωc附近,且由于其边频为奇数次调制波频率,即(2l-1)ωs,因此谐波呈奇数次分布;
谐波幅值为 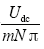
(3)谐波频率为2m(2N-1)ωc±(2l-1)ωs,谐波分布在2m(2N-1)倍的ωc附近,且其边频为奇数次调制波频率,即(2l-1)ωs,因此谐波呈奇数次分布;谐波幅值为 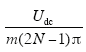
综合分析可知,高频谐波uzan分布在mN倍的载波频率即mNωc附近,呈奇数次分布,但在谐波点(2m-1)×(2N-1)ωc、m×2Nωc和m×(2N-1)ωc存在3个不同的谐波特征,m=1, 2, 3, …。
3.2.2 iza的谐波特性
同理,参照第2.2.2节,定义iza的低频调制分量和高频开关分量分别为izas、izan。
(1)低频调制分量izas
根据式(14)和式(15),求得izas
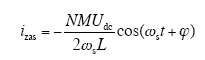
比较式(11)和式(18)可知,对于低频调制分量来说,并联系统输出总电流izas在相位上与单模块输出电流ias同步,在幅值上提高了N倍,这符合并联系统扩容的主要功能要求。
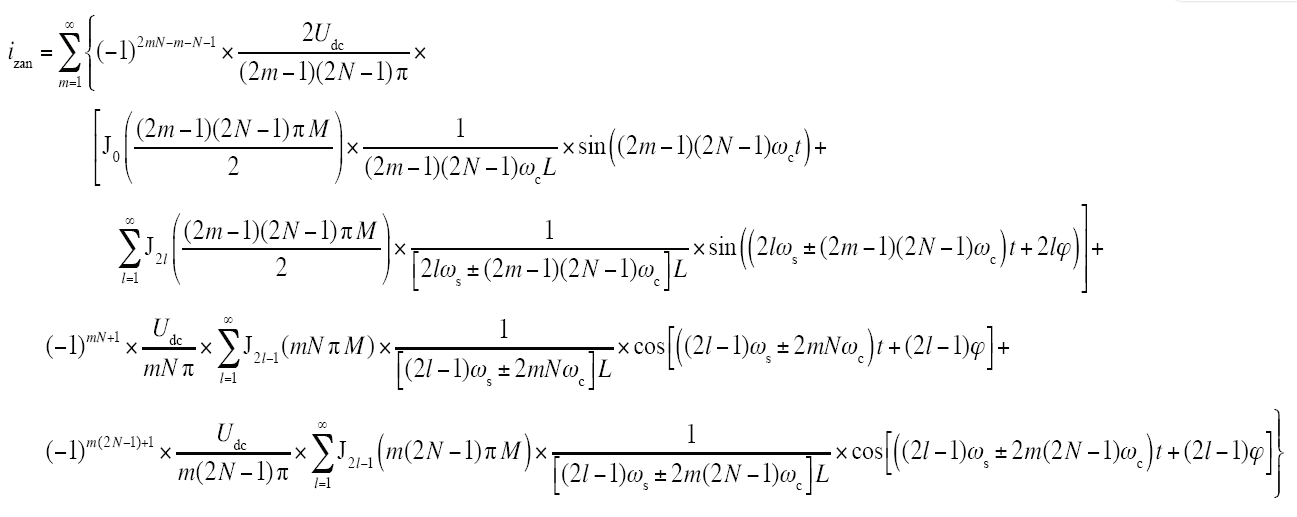
(2)高频开关分量
同理,根据式(14)和式(17),可求得izan
分析式(19)izan的谐波特性:
(1)谐波分布特性。类似于uzan的分布特性,izan分布在mN倍的载波频率即mNωc附近,呈奇数次分布,m=1, 2, 3, …;相比较于ian,izan的谐波频率提高了N倍。
(2)幅频特性。由于通常情况下ωcL>1,且ωc>>ωs,忽略含有ωs数值项的影响,则相比较于ian,在频率点mNωc处,幅值降低N倍,且在ωcL既定情况下,随着m和N的增长,频率mNωc越高,幅值衰减越多。
上述结论表明,基于CPS-SPWM开关调制技术的并联系统,输出电流的高频开关分量的频率与并联数N成正比,而幅值与N成反比。
4 实验分析
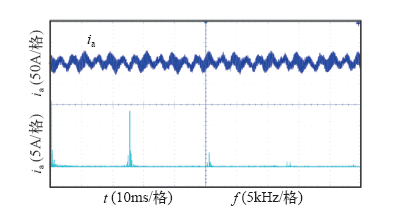
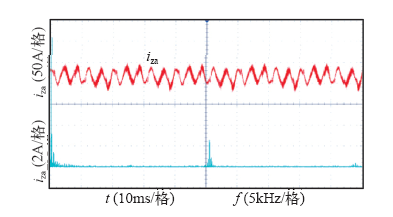
按照图3搭建APF并联系统实验平台,并联数N=2。系统参数设置:系统电压400V;滤波电感L=0.3mH,直流电容C=5 000μF;开关频率fc取12.8kHz,负载为三相不控整流器带电阻负载。
图4
图4
单模块输出电压波形及其FFT频谱图
Fig.4
The experiment graph and its FFT frequency spectrum of the single-module output voltage
图5
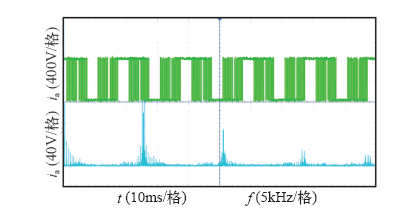
图5
单模块输出电流波形及其FFT频谱图
Fig.5
The experiment graph and its FFT frequency spectrum of the single-module output current
图6
图6
并联装置输出总电流波形及其FFT频谱图
Fig.6
The experiment graph and its FFT frequency spectrum of the total output current
图4为单个模块输出电压的波形和FFT频谱,可见,高频开关频率主要分布在m×12.8kHz附近,m=1, 2, …,这符合式(10)的结论。
5 结论
通过上述对基于对称规则采样法的APF单模块SPWM电压、电流谐波特性以及多模块并联系统CPS-SPWM电压、电流谐波特性的理论分析及实验验证,可知:
(1)低频调制谐波特性。相比较于单个模块输出电流ias,并联系统输出总电流izas在相位上与之同步,在幅值上提高了N倍,这符合并联系统扩容的主要功能要求。
(2)高频开关谐波特性。①谐波分布特性:并联系统输出电流的高频谐波izan主要分布在mN倍的载波频率即mNωc附近,呈奇数次分布,m=1, 2, 3, …;但在(2m-1)×(2N-1)ωc、m×2Nωc和m×(2N-1)ωc三个载波频率分布点,高频谐波的幅值分布存在3种变化规律;②幅频特性:相比较于单个模块输出电流ian,izan的高频谐波频率提高了N倍,在频率点mNωc处,幅值降低了N倍,并且,在ωcL既定情况下,随着m和N的增长,频率mNωc越高,幅值衰减越多。
(编辑:郭丽军)
参考文献
Application issues of active power filters
[J].
Dynamic interaction analysis of APF systems
[J].
DOI:10.1109/TIE.2013.2289896
Magsci
[本文引用: 1]

This paper discusses the dynamic interaction of multi active power filters (APFs) paralleled with a weak power grid. In order to analyze the dynamic interaction from multi APFs, the output impedance of an APF is solved. The influences of both circuit and control parameters on the output impedance are analyzed. Based on the output impedance of an APF, the dynamic influences of an APF on the other APF connected to the weak grid are discussed. As shown in this paper, the stability of an APF is improved with an increased output filter inductance and some control parameters to reduce its bandwidth. The proposed analysis methods can be used not only for multi APFs but also for the other multi-inverters connected to a weak grid. Experimental tests are carried out using two paralleled three-phase 10-kVA inverters to confirm the validity of the theoretical analysis.
APF for harmonic voltage resonance suppression in distribution system
[C].
基于LCL滤波器的并联有源电力滤波器电流闭环控制方法
[J].并联有源电力滤波器(active power filter,APF)需要具有较高的补偿带宽和较低的开关纹波含量。LCL滤波器由于可以兼顾低频段增益和高频段的衰减,是APF输出滤波器的较好选择,但LCL滤波器是3阶系统,增加了控制难度。通常应用于APF电流控制的瞬时值反馈内环结合重复控制外环的双环控制性能较好,但其主要是针对单电感滤波器进行设计,难以直接应用于LCL滤波器控制。提出一种简单的内环方案,利用数字控制固有的一拍计算延时进行LCL滤波器的稳定控制,只需一个反馈量,结构简单;由于内环有效地改善了系统的特性,作为外环的重复控制器的设计相对简单。基于LCL滤波器的双环控制方案赋予了系统较高的稳态补偿精度和快速的动态响应。实验结果证明了所提出控制方法的有效性。
Current Loop control approach for LCL-based shunt active power filter
[J].并联有源电力滤波器(active power filter,APF)需要具有较高的补偿带宽和较低的开关纹波含量。LCL滤波器由于可以兼顾低频段增益和高频段的衰减,是APF输出滤波器的较好选择,但LCL滤波器是3阶系统,增加了控制难度。通常应用于APF电流控制的瞬时值反馈内环结合重复控制外环的双环控制性能较好,但其主要是针对单电感滤波器进行设计,难以直接应用于LCL滤波器控制。提出一种简单的内环方案,利用数字控制固有的一拍计算延时进行LCL滤波器的稳定控制,只需一个反馈量,结构简单;由于内环有效地改善了系统的特性,作为外环的重复控制器的设计相对简单。基于LCL滤波器的双环控制方案赋予了系统较高的稳态补偿精度和快速的动态响应。实验结果证明了所提出控制方法的有效性。
Control strategy and site selection of a shunt active filter for damping of harmonic propagation in power distribution systems
[J].
Control of a multimodule parallelable three-phase active power filters
[C].
基于载波移相并联的直驱风力发电并网变流器控制策略
[J].并联有源电力滤波器(active power filter,APF)需要具有较高的补偿带宽和较低的开关纹波含量。LCL滤波器由于可以兼顾低频段增益和高频段的衰减,是APF输出滤波器的较好选择,但LCL滤波器是3阶系统,增加了控制难度。通常应用于APF电流控制的瞬时值反馈内环结合重复控制外环的双环控制性能较好,但其主要是针对单电感滤波器进行设计,难以直接应用于LCL滤波器控制。提出一种简单的内环方案,利用数字控制固有的一拍计算延时进行LCL滤波器的稳定控制,只需一个反馈量,结构简单;由于内环有效地改善了系统的特性,作为外环的重复控制器的设计相对简单。基于LCL滤波器的双环控制方案赋予了系统较高的稳态补偿精度和快速的动态响应。实验结果证明了所提出控制方法的有效性。
Control strategy for direct-drive wind generation grid side converter based on carrier phase shifting parallel
[J].并联有源电力滤波器(active power filter,APF)需要具有较高的补偿带宽和较低的开关纹波含量。LCL滤波器由于可以兼顾低频段增益和高频段的衰减,是APF输出滤波器的较好选择,但LCL滤波器是3阶系统,增加了控制难度。通常应用于APF电流控制的瞬时值反馈内环结合重复控制外环的双环控制性能较好,但其主要是针对单电感滤波器进行设计,难以直接应用于LCL滤波器控制。提出一种简单的内环方案,利用数字控制固有的一拍计算延时进行LCL滤波器的稳定控制,只需一个反馈量,结构简单;由于内环有效地改善了系统的特性,作为外环的重复控制器的设计相对简单。基于LCL滤波器的双环控制方案赋予了系统较高的稳态补偿精度和快速的动态响应。实验结果证明了所提出控制方法的有效性。
A comprehensive study of harmonic cancellation effects in interleaved three-phase VSCs
[C].
Interleaving impact on harmonic current in DC and AC passive components of paralleled three-phase voltage-source converters
[C].
数字控制高频变换器的新颖PWM方法
[J].
A novel PWM technique in high-frequency converter controlled by digital system
[J].
A novel sampling method of SPWM with nonsymmetrical rules
[J].