1 引言
同步电机具有体积小、损耗低且效率高等优点,在节约能源和保护环境日益受到重视的今天,更是以其卓越的性能,被广泛地应用于国民经济的各个领域。所以,对其进行深入研究就显得非常必要。
Ansoft和Ansys是文献中常用的电磁场有限元软件,Ansoft只能计算静态电磁场,不能分析运动场,Ansys可以计算电机的运动过程,但是脚本编辑能力弱且入门所需时间长。
综合比对三种常用的电磁场有限元软件,本文选用Magnet分析励磁同步电机的电气参数。计算主要有三步:前处理、求解和后处理分析。①前处理。依据选取的凸极三相4极励磁同步电机参数在Magnet中构建2D模型,拉伸至3D模型,设置各部件材料属性,然后生成线圈,设定电机初始位置和运动,进行自适应网格剖分;②求解。2D暂态求解器(Newton和CG迭代法);③后处理。依据Magnet计算所得数据导入Matlab绘制波形并对比数据分析。根据该电机模型在空载情况下的计算结果分析驱动电源的频率对电机转速、定子/转子铜损、铁损、涡流损耗及磁感应强度的影响,为励磁同步电机的设计提供理论依据。
2 模型建立
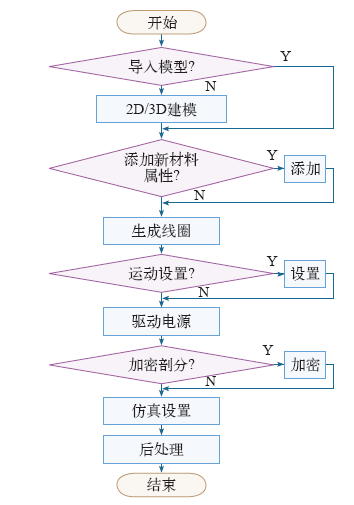
计算总体步骤如图1所示。
图1
2.1 电机参数
表1 电机尺寸及相关参数
Tab.1
| 参 数 | 数 值 | 参 数 | 数 值 | |
|---|---|---|---|---|
| 额定电压/V | 220 | 频率/Hz | 50 | |
| 定子内径/cm | 3.9 | 定子外径/cm | 6.4 | |
| 定子极对数 | 2 | 定子槽数 | 12 | |
| 转子直径/cm | 7.4 | 电机轴长/cm | 5 | |
| 电机轴半径/cm | 1.5 |
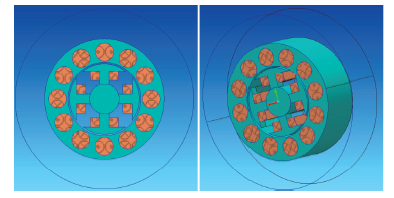
2.2 材料属性
图2
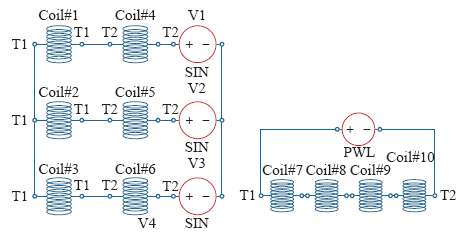
2.3 生成线圈及电源驱动
图3
2.4 电机运动设置
Motion指的是对电机所有运动部件(轴、转子和转子线圈)设定转动初速度、初角度和选择方向。本文将模型中的电机轴、转子和转子线圈的运动设置为:初速度为0,初角度为0,以原点为圆心,沿着Z轴方向旋转。
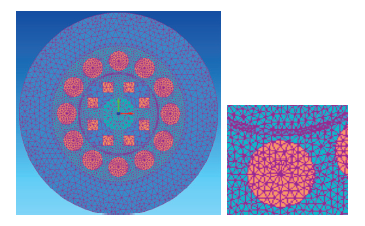
2.5 剖分及仿真参数设置
图4
3 仿真结果分析
3.1 频率f与磁场能量分布的关系
Tab.2 Relationship between frequency and maximum of B at different time (单位:T)
| f /Hz | t /ms | |||
|---|---|---|---|---|
| 20 | 40 | 60 | 80 | |
| 35 | 4.250 | 3.934 | 3.967 | 4.126 |
| 40 | 3.649 | 3.747 | 3.586 | 3.802 |
| 45 | 3.250 | 3.527 | 3.683 | 3.516 |
| 50 | 3.204 | 3.456 | 3.532 | 3.394 |
| 55 | 3.015 | 3.153 | 3.448 | 3.205 |
表3 频率与磁场最大值Bm的对应关系
Tab.3
| f /Hz | 35 | 40 | 45 | 50 | 55 |
|---|---|---|---|---|---|
| B /T | 4.991 | 4.677 | 4.494 | 4.444 | 4.367 |
一段载流I,长为L的直导线磁场分布符合
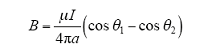
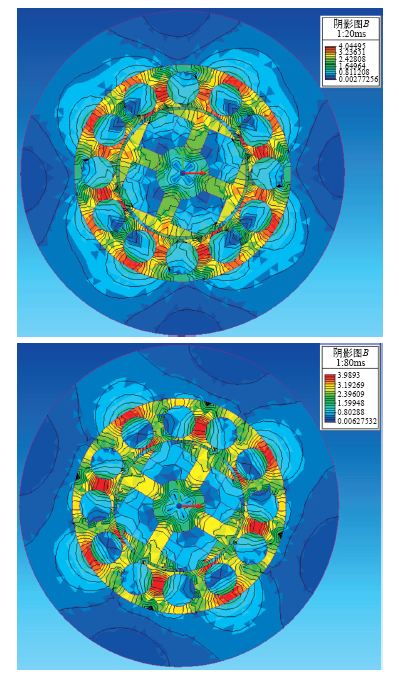
图5分别给出f = 35Hz,t = 20ms和t = 80ms时电机定转子内部的磁场强度分布云图。
图5
图5
f = 35Hz,t = 20ms和t = 80ms对应的能量分布云图
Fig.5
|B| shaded plot of 35Hz at t = 20ms and t = 80ms
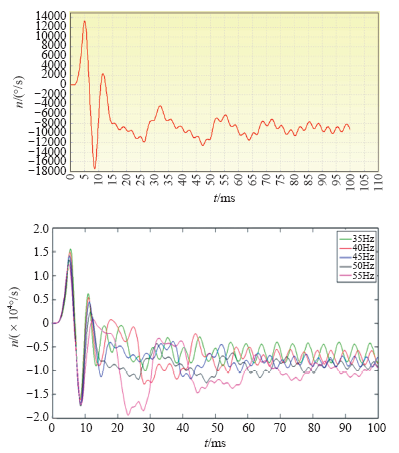
3.2 频率f与电机转速n的关系
电源频率f与电机转速之间满足
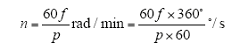
式中,f为电源频率;p为极对数;n为转子转速。
从图6可以看出,t = 0~15ms为电机起动过程,t = 16~100ms电机进入平稳过程,对比式(2),符合f与n成正比的结论。
图6
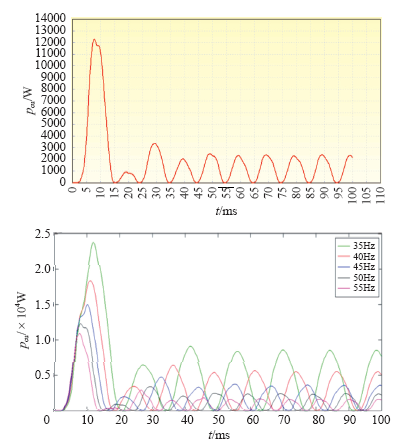
3.3 频率f与铜损的关系
铜损计算公式为
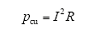
图7
图8
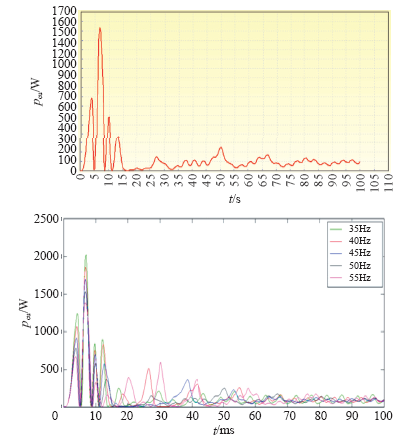
3.4 频率f与其他损耗的关系
铁损的计算公式为
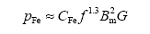
式中,CFe为铁耗系数与硅钢片材料有关;G为硅钢片的重量。
涡流损耗的计算公式为
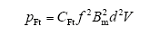
式中,CFt为涡流损耗系数,大小取决于电阻率ρ;d为材料厚度。
表4 频率与其他损耗的对应关系
Tab.4
| f/Hz | 35 | 40 | 45 | 50 | 55 |
|---|---|---|---|---|---|
| Bm/T | 4.991 | 4.677 | 4.494 | 4.444 | 4.367 |
| 铁损/kW | 2.533 | 2.646 | 2.847 | 3.193 | 3.935 |
| 涡流损耗/kW | 30.51 | 34.99 | 40.90 | 49.37 | 65.04 |
4 结论
本文用有限元软件Magnet完成励磁同步电机的电磁场计算,Matlab实现数据的后处理分析,讨论了电机重要电气性能参数——磁感应强度、转速、铜损、铁损及涡流损耗与驱动电源频率之间的关系。
通过研究,得出以下结论:
(1)频率f增大,磁感应强度B相应地减小,但其减小率低于f的增长率,则铁损和涡流损耗相应地增加,涡流损耗增长率较大。电机设计过程中,为尽可能减小涡流损耗和铁损,可以适当降低电源频率。
(2)频率f增大,电流相应地减小,则转子和定子的铜损相应地减小。
(3)频率f增大,转速相应地增加。如应用于对转速上限严格要求的场合,可适度降低频率。
本文以凸极三相4极励磁同步电机为例,说明Magnet有限元分析方法在电机设计中的应用,该方法同样适用于其他类型的电机。
参考文献
切向磁钢混合励磁同步电机空载磁路计算及三维场分析
[J].
YanYangguang, Su Kaicheng. Magnetic circuit calculation and 3-Dimensional field analysis of IPM hybrid excitation synchronous machine under no-load condition
[J].
稀土永磁同步电动机磁路计算方法
[J].
Calculating method of magnetic circuit for rare-earth PM synchronous motor
[J].
The shape design of permanent magnet for permanent magnet synchronous motor considering partial demagnetization
[J].
Ansoft 软件在同步发电机设计中的应用
[J].
Application of Ansoft software in design of synchronous generator
[J].
基于Ansys 的电励磁同步电机温度场分析
[J].
Analysis of temperature field for electrically excited synchronous motor based on Ansys
[J].
基于Ansoft的ALA转子同步电机磁场及参数计算
[J].
The magnetic field distribution and parameters computation for synchronous machine with ALA rotor by Ansoft software
[J].
外转子永磁同步发电机的Magnet仿真分析
[J].
Magnetic simulation for outer-rotor permanent-magnet synchronous generators
[J].
基于Magnet的永磁同步发电机设计
[J].
Design of permanent magnet synchronous generator based on Magnet
[J].
高压换流变压器损耗计算程序
[J].
Additional loss calculation program of HV converter transformer
[J].
四相电励磁双凸极发电机转子极加宽对外特性的影响
[J].
Influence on output characteristics wound-field doubly salient generators with a widened rotor pole
[J].
双凸极永磁电动机磁阻转矩和转矩脉动的关系研究
[J].
Research on relationship between reluctant torque and torque ripple for doubly salient permanent magnet motor
[J].
同步电机定子与气隙流场数值计算与分析
[J].
Feng fan, Sun Mingqi, et al. Numerical calculation and analysis of fluid flow field of stator and air-gap of a synchronous machine
[J].
定转子电阻对同步电机瞬态时间常数影响
[J].
Influence of stator and rotor resistances on transient time constant of synchronous machine
[J].
新型结构永磁屏蔽电机三维磁场分析和电感计算
[J].
Analysis of 3-Dimensional field and calculation of inductance for a new structure of a permanent magnet canned motor
[J].
电励磁双凸极发电机转子极宽对输出特性的影响
[J].
Influence of rotor pole width on output characteristic of doubly salient electro-magnetic generator
[J].