电气工程学报, 2015, 10(10): 37-43 doi:

理论研究

电子式电压互感器暂态响应的影响因素分析

刘琦1, 徐雁1, 高飞2, 程昱舒2, 赵园2, 肖霞1

1. 华中科技大学光电互感器研发中心 武汉 430074

2. 国网山西省电力公司计量中心 太原 030001

Simulation Research on Electronic Voltage Transformer Transient Process

Liu Qi1, Xu Yan1, Gao Fei2, Cheng Yushu2, Zhao Yuan2, Xiao Xia1

1. Optic-Electrical Transformer Research and Development Center Huazhong University of Science and Technology Wuhan 430074 China

2. Shanxi Electric Power Company State Grid Metering Center Taiyuan 030001 China

责任编辑: 杨晓花

收稿日期: 2015-08-26   网络出版日期: 2015-10-25

Editor: Yang Xiaohua

Received: 2015-08-26   Online: 2015-10-25

作者简介 About authors

刘琦, 男 1991年生,硕士研究生,主要从事电子式互感器的研究。

徐雁, 女 1963年生,博士,硕士生导师,主要从事电力系统电磁测量方面的科研及教学工作。

摘要

电子式电压互感器的暂态特性直接决定其在投入电网后能否稳定运行,基于电容分压的电子式电压互感（ECVT）暂态过程主要与电容分压器及负载相关。从理论上分析了电容分压器二次负载电阻及电容器内阻对ECVT暂态特性的影响;对220kV ECVT进行建模,仿真分析了二次负载电阻和电容器串联内阻对短路及重合闸暂态过程的影响,对不同的系统重合闸动作时限给出了相应的二次负载电阻值的最佳取值范围,找出了电容器串联内阻对暂态特性影响的规律。仿真结果表明,对所研制的ECVT,二次负载电阻取300〜500kΩ为最佳,高、低压侧电容器串联内阻之比是分压比为最佳。本文的实验结果显示,合理选择电容器和二次负载电阻可以改善暂态特性。

关键词： 电子式电压互感器 ; 短路 ; 重合闸 ; 暂态过程 ; 电容分压器

Abstract

When an electronic voltage transformer is put into the power system,whether it works stably depends on its transient behavior,the transient process of the electronic voltage transformerbased on capacitive（ECVT） voltage is mainly related to capacitive voltage divider and the part connected to it. The influence of the capacitive voltage divider’s load resistance and internal resistance for ECVT is analysed in theory. A simulation model is built for a 220kV ECVT to simulate the influence of the capacitive voltage divider’s load resistance and internal resistance in short-circuit and reclosing transient, and the best range of load resistance for different reclosing time is given, the law of capacitor internal resistance’s impact on transient characteristics is found out.Simulation results show that for the researched ECVT ,the load resistance takes 300~500kΩ as the best,the high-low capacitor series resistance ratio is best to be equal to the voltage ratio.This paper’s experimental data shows that selecting capacitor and load resistance reasonably can improve the transient characteristics.

Keywords： Electronic voltage transformer ; short-circuit ; reclosing ; transient process ; capacitor voltage divider

PDF (2320KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘琦, 徐雁, 高飞, 程昱舒, 赵园, 肖霞. 电子式电压互感器暂态响应的影响因素分析. 电气工程学报[J], 2015, 10(10): 37-43 doi:

Liu Qi. Simulation Research on Electronic Voltage Transformer Transient Process. Journal of Electrical Engineering[J], 2015, 10(10): 37-43 doi:

1 引言

随着电力系统电压等级的提高及容量的增大,以及测量和保护要求的不断完善,传统的电磁式和电容式电压互感器的不足日益突出,都存在着绝缘结构复杂、动态范围窄、易铁磁谐振、体积大和输出信号易受电磁干扰等缺点,电子式电压互感器有着无铁心、无铁磁谐振、能抗电磁干扰等优点[1-2]。此外,随着系统测量和保护向智能化、微机化方向发展,电子式电压互感器输出的数字信号可以直接与微机保护装置接口,能配合计算机采用数字信号处理技术,有取代传统互感器的趋势。

目前,以基于电容分压的电子式电压互感器（ECVT）应用最为广泛[3-5]。电子式电压互感器已经在很多地方挂网运行,但是由于其性能不完善,使得实际使用中暂态情况不理想。

现阶段对EVCT暂态过程的研究大多基于理论上的定性分析,没有结合ECVT的结构进行具体的分析。本文首先从理论上分析基于电容分压的电子式电压互感器在短路和重合闸时的暂态特性,进而建模进行仿真分析,结合ECVT的结构讨论了二次负载电阻及电容器内阻对其暂态特性的影响。

2 ECVT的工作原理及理论分析

2.1 ECVT的工作原理

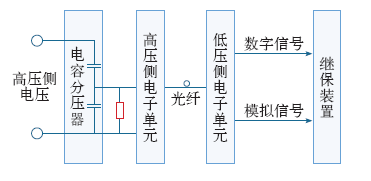
ECVT主要由电容分压器、高压侧电子单元、低压侧电子单元三大部分组成,如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   ECVT 工作原理图

Fig.1   Working diagram of ECVT


采用电容分压器对电网高电压进行分压,将电压降至较低水平,之后高压侧电子单元对其进行处理、采样,再通过电/光转换耦合进光纤。光纤实现高压侧与低压侧的隔离,并将被测信号传输到主控室的低压侧电子单元,经过光电转换恢复出被传数据,进行处理操作[6]。

由于高低压侧通过光纤传输信号实现了电隔离,在暂态过程中,后级电路不会受到前级电路的影响,因此,影响ECVT暂态过程的主要是电容分压器及与之连接的高压侧电子单元。

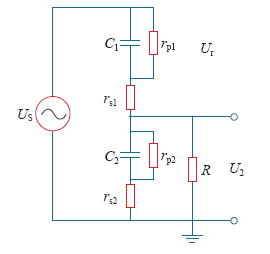
电容分压器是ECVT的信号获取单元,其实际工作原理如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   电容分压器的实际工作原理图

Fig.2   Schematic diagram of capacitor voltage divider


图中,C1、C2分别为高、低压臂电容;rs1、rp1分别为C1的串、并联内阻;rs2、rp2分别为C2的串、并联内阻;R为高压侧电子单元的等效输入阻抗,即电容分压器的二次负载电阻;US为被测一次电压,U1为高压臂上的电压;U2为经电容分压器分压之后的输出电压,也是高压侧电子单元的输入电压。

2.2 稳态情况的理论分析

理想情况下,电容器内阻rs1、rs2→0,rp1、rp2→∞,R→∞,高、低压侧电容串联分压,故有

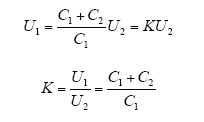
式中,K为分压比。

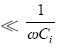
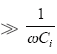
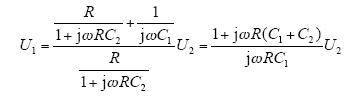
实际工作情况下,rsi ,rpi （i =1,2）,负载电阻R为有限值,电阻R参与分压,可得

即实际分压比为

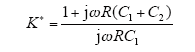
所以,实际电压比Kv*,比差ΔK*和相差φv分别为

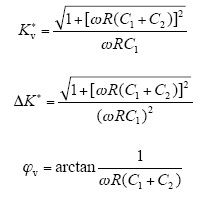
可见,R的大小不仅影响分压比,还影响高低压侧相位差,当R较小时,会导致比差过大、相偏过大等问题,所以在实际应用中,为满足稳态要求,电阻R的阻值一般取100kΩ以上。

2.3 暂态过程的理论分析

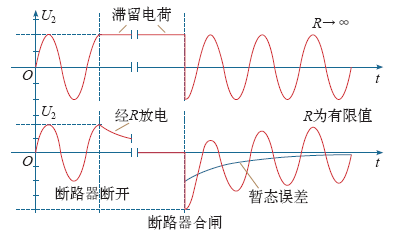
除正常稳态工作条件外,ECVT的许多暂态过程必须纳入考虑,一方面是保护电网元件所需,另一方面也要求ECVT能够承受一定范围的异常工作条件[7-9]。对用电容分压器作为传感器的电子式电压互感器,最严重的暂态条件是带滞留电荷重合闸和高压端对地短路,因此,下面对这两类暂态过程进行分析。

当一条线路或电缆被断开时,ECVT上可能有电荷滞留[10]。此过程中电容器上所带的滞留电荷量取决于断开时电压的相位,讨论线路在波峰处断开,在波谷处合闸,则

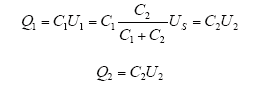
高压臂电容C1上的滞留电荷一般不易释放,而低压臂电容C2上的滞留电荷会经电阻R放电,时间常数为

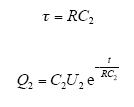
t时间后再次合闸,由于线路经直流低阻抗放电,使得C1上的电荷加到C2上,即

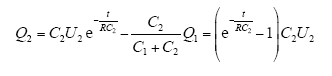
C2上的电荷在合闸后以直流电压的形式叠加到二次电压上,对后级电路造成很大的影响,电荷量越多越严重。图3给出了重合闸过程的原理图。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   重合闸过程的原理图

Fig.3   Schematic diagram of the coincidence process


由图3可知,R的大小将直接影响到滞留电荷放电时间的长短以及合闸后二次电压相对与稳态电压的误差大小,一方面,当断路器断开时,低压臂电容会通过电阻R放电,由于在放电过程中产生的电压差会使得合闸后在交流电压上叠加直流量,所以应该尽可能少地放电,从而尽可能少地叠加直流量,最理想的情况是在R→∞时,滞留电荷无法通过R放电,重合闸时不会在原正弦电压上叠加直流分量,不会产生暂态误差,从这方面考虑,希望R越大越好。另一方面,在合闸开始时,二次电压上所叠加的直流量会通过电阻R放电,应该尽快放电以消除直流分量的影响,此过程希望R越小越好。

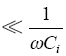
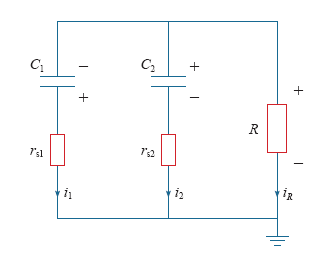
由于电容分压器的串联内阻很小,一般在μΩ~mΩ级别,故而重合闸全过程中电容分压器的串联内阻rs1 ,rpi ,对此过程的影响很小,可以忽略不计,影响重合闸过程的主要是高压侧电子单元的等效输入阻抗。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   短路时刻的等效电路图

Fig.4   Equivalent circuit diagram of short-circuit moment


高压端单相对地短路时,高压端子直接接地,ECVT等效电路如图4所示,设分压电容上C1和C2的电压分别为UC1、UC2,短路瞬间C1、C2上的电压分别为UC1(0+)和UC2(0+),取向下为电流的正方向,C1、C2上通过的电流分别是i1、i2,R上通过的电流为iR,C1、C2的串联内阻分别是rs1和rs2。

由KCL,得

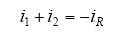
由KVL,得

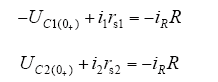
解得

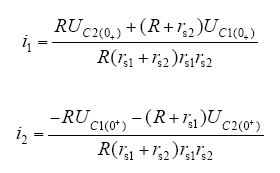
所以,R上电压为

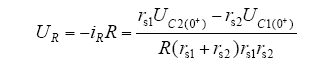
又

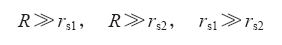
故而

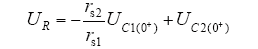
而

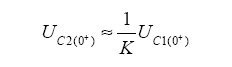
所以

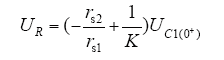
短路瞬间,UC1(0+)为负值,R上电压初值取决于两电容的内阻之比,当rs1 = Krs2时,UR上没有冲击电压,最为理想。

3 ECVT暂态过程的仿真分析

3.1 建立模型

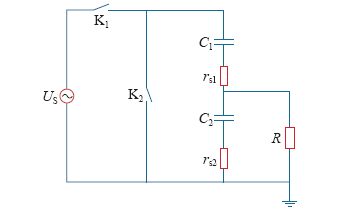
为验证上述理论分析进行仿真分析。国家标准GB/T 20840.7—2007要求高压电力电容器的tan δ应小于0.5%,因为电容器的并联内阻非常大,对暂态过程的tan δ几乎没有影响[11-12],可以忽略。故而建立如图5所示的仿真模型,通过开关K1模拟重合闸过程,通过开关K2模拟高压端单相对地短路过程。

图5中C1、C2分别为高、低压臂电容;U1为高压线路电压;R为高压侧电子单元的等效输入阻抗,即电容分压器的二次负载电阻。针对220kV的ECVT进行仿真,电容分压器的高、低压臂电容值分别为C1 = 5.002nF,C2 = 12.7μF,分压比为2 538.98,rs1和rs2分别取1Ω和0.004Ω,额定输入电压为220/kV,所选电容分压器的tan δ = 0.06%,电容器的并联内阻很大,不予以考虑。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   仿真电路图

Fig.5   Simulation circuit diagram


3.2 电容分压器的负载电阻对重合闸暂态的影响

仿真时针对最严重的暂态情况进行研究,即波峰处开路,波谷处合闸。根据运行经验,重合闸动作时限一般取0.5~1.5s[13-16],考虑二次重合闸情况,以0.6s为重合闸的时间间隔,取0.005s时断开K1,0.615s时合上K1,而后于0.705s时断开K1,1.315s时合上K1,两次均是波峰处断开波谷处合闸。当R = 200kΩ时仿真得到的二次电压随时间变化的波形如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   重合闸过程的波形图

Fig.6   Waveform chart of the coincident gate process


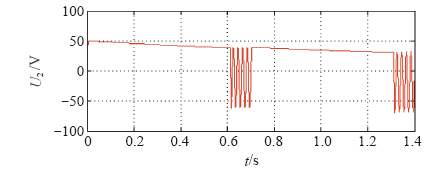
由图6可知,第二次重合闸与第一次的情况一样,相当于延长了重合闸的间隔时间,因此针对第一次重合闸进行研究。

由上述理论分析可知,当二次负载电阻R大小发生变化时,暂态误差不同,因此当重合闸时间间隔为0.6s时改变R值对此过程进行仿真。

国家标准GB/T 20840.7—2007要求在合闸后2~3个周期内瞬时电压误差ε%应小于10%。其中

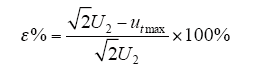
式中,utmax为暂态过程中二次电压的最大值;U2为稳态情况下二次输出电压的额定值。

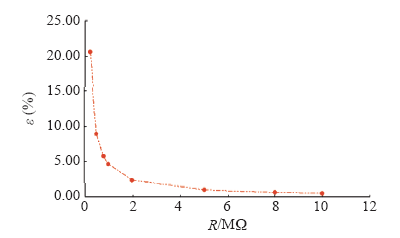
按标准要求在合闸后第3个周期的波峰处记录电压误差,通过多次仿真得到电阻R的值与电压误差ε(%)的关系如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   二次电阻大小与暂态误差之间的关系

Fig.7   The relationship between the load resistance value and the voltage error


由图7可知,当R的大小为300kΩ时,电压误差已经在10%以内,已经符合要求,继续增大其阻值虽然可以使电压误差更小,然而电阻的增大可能会导致阻值不稳定等问题,故而当重合闸时间间隔为0.6s时电阻一般取300〜800kΩ为宜。

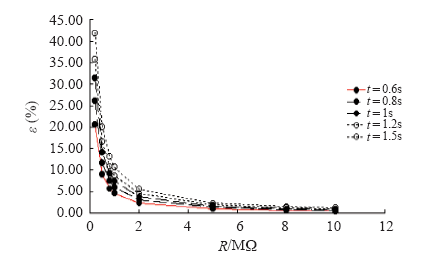
由于重合闸的两个过程都对R值有限制,需要同时考虑两方面的影响,故而重合闸的时间间隔对此过程同样有影响,当重合闸时间t分别为0.8s、1.0s、1.2s、1.5s时对不同R值的情况下重复上述过程进行仿真,得到不同重合闸时间间隔时电阻R对暂态误差影响的关系如图8所示。

由图8可知,相同电阻的情况下,重合闸时间间隔越长,暂态误差越大。当重合闸时间间隔为1.5s时,二次负载电阻值必须达到2MΩ才能满足标准要求。因此对不同的系统应选择合适的二次分压电阻。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   不同重合闸时间间隔时二次电阻大小与暂态误差之间的关系

Fig.8   The relationship between the load resistance value and the voltage error for different re-close time


3.3 电容分压器的串联内阻和二次负载电阻对单相对地短路的影响

高压端单相对地短路时,C1高压端接地,C1和C2并联,电容上的电荷通过电阻R放电,最严重的情况是电压峰值时短路,按照标准GB/T 20840.7—2007的要求,此时输出电压应在一周波内下降到短路前峰值的10%以下。

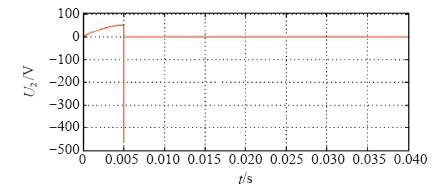
为满足重合闸过程的要求,选取R = 300kΩ进行短路过程的仿真,当rs1 = 0.1Krs2,R = 300kΩ时,仿真得到二次电压随时间的变化如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   一次短路时二次电压随时间变化的波形（R = 300kΩ,rs1 = 0.1Krs2）

Fig.9   Waveform of secondary side voltage varying with time in the primary side short-circuit moment（R = 300kΩ,rs1 = 0.1Krs2）


由图9可见,此时有很大的负向冲击电压,此电压在很短的时间内释放,在此过程中,由于电压过高可能会对电路器件造成不可恢复的损伤。

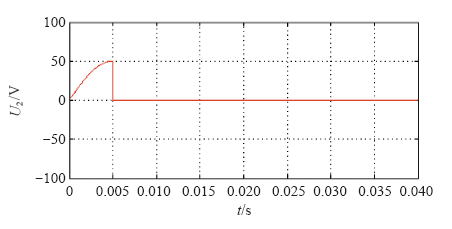
当rs1 = Krs2,R = 300kΩ时,仿真得到的二次电压随时间的变化关系分别如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   一次峰值短路时二次电压随时间的变化（R = 300kΩ）

Fig.10   Waveform of secondary side voltage varying with time in the primary side short-circuit moment（R = 300kΩ）


由图10可知,当高压侧电子单元的等效输入阻抗值很大时也没有出现电压在一个周波内无法降到指定范围的情况,这是由于在极短的放电时间内,会产生很大的电流流过电容器的串联内阻,负载电阻上的负向冲击很小,以致暂态冲击的最大值已经小于稳态电压峰值的10%,所以也可以满足条件,与上面的理论分析相符合。

可以看到,当负载电阻R = 300kΩ时,继续增大R的值几乎不会对短路过程产生影响,重合闸过程要求R≥300kΩ,当R达到此级别时,短路过程受高压侧电子单元的等效输入阻抗的影响已经很小,此时,影响短路暂态过程的主要是高低压侧电容的串联内阻之比λ为

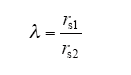
调整高、低压侧电容串联内阻比,继续进行仿真,得到结果如下表所示。其中,U2m为二次电压的峰值。

表1   负载电阻为300kΩ时电容内阻比λ与负载电阻上冲击电压的关系

Tab1  The relationship between the ratio of capacitance resistance and impulse voltage when the load resistance is 300kΩ

内阻比λU2 /V内阻比λU2 /V
0.01K-95.296U2m0.5K-U2m
0.1K-8.97U2m0.8K-0.25U2m
0.2K-3.99U2m1K0
0.3K-2.32U2m2K0

新窗口打开| 下载CSV


如上表所示,当λ K,对地短路时没有负向冲击,由于 ,故而正向的冲击也很小,与短路时的下降波形重合;而当λ K时,有非常明显的负向冲击,其最大值为- 4 764.8V,是稳态二次电压峰值的96.296倍。因此,分压器高低压侧电容的内阻之比应大于或等于分压比K。一般实际结构中高压侧采用多个电容串联组成,而低压侧采用多个电容并联而成,尽管如此,高低压侧电容的串联内阻之比仍然要小于分压比,从而使得暂态特性不佳。

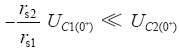
4 结论

对ECVT重合闸过程影响最大的是二次负载电阻,其阻值大小直接影响重合闸过程的暂态误差。对于所选的电子式电压互感器,二次负载电阻应根据所应用系统的重合闸时间间隔合理的选取300kΩ~2MΩ,针对不同的互感器合理的设计二次负载电阻可以改善其暂态特性。单相对地短路时,二次负载电阻对暂态过程的影响不大,此过程中起主要影响作用的是高低压电容器的串联内阻之比,串联内阻之比应该大于或等于分压比。

参考文献

Christensen L H .

Design construction and test of a passive optical prototype high voltage instrument transformer

[J]. IEEE Trans. PD, 1995,10(3):1332-1337.

[本文引用: 2]

段雄英, 廖敏夫, 邹积岩 .

基于电容分压器的电子式电压互感器的研究

[J]. 高电压技术, 2003(1):50-51,59.

[本文引用: 2]

Duan Xiongying, Liao Minfu, Zou Jiyan .

Electronic voltage transformers based on capacitive voltage divider

[J]. High Voltage Engineering, 2003(1):50-51, 59.

[本文引用: 2]

冯建勤, 王庆铭, 丁莉芬 , 等.

电子式电压互感器的研究现状和展望

[J]. 变压器, 2010(11):40-43.

[本文引用: 2]

Feng Jianqin, Wang Qinmin, Ding Lifen , et al.

Present research situation and trend of electronic voltage transformer

[J]. Transformer, 2010(11):40-43.

[本文引用: 2]

李伟凯, 郑绳楦 .

高压电压互感器精密电容分压器的研究与设计

[J]. 传感技术学报, 2005(3):634-637,656.

[本文引用: 2]

Li Weikai, Zheng Shengxuan .

Study and design of high voltage potential transformer using precise capacitive voltage divider

[J]. Chinese Journal of Sensors and Actuators, 2005(3):634-637, 656.

[本文引用: 2]

时德钢, 刘晔, 胡光辉 , 等.

一种基于电容分压的电子式电压互感器

[J]. 电力电容器, 2003(4):1-3,12.

[本文引用: 1]

Shi Degang, Liu Ye, Hu Guanghui , et al.

Electronic voltage transformer based on capacitive voltage dividing

[J]. Power Capacitor, 2003(4):1-3, 12.

[本文引用: 1]

罗苏南, 南振乐 .

基于电容分压的电子式电压互感器的研究

[J].高电压技术, 2004(10):7-8,14.

[本文引用: 2]

Luo Sunan, Nan Zhenle .

Electronic voltage transformers based on capacitive voltage divider

[J]. High Voltage Engineering, 2004(10):7-8, 14.

[本文引用: 2]

Slomovitz D .

Electronic based high-voltage measuring transformers

[J]. IEEE Transactions on Power Delivery, 2002,17(2):359-361.

DOI:10.1109/61.997899      URL     [本文引用: 2]

Pan Feng, Chen Ruimin, Xiao Yong , et al.

Electronic voltage and current transformers testing device

[J]. Sensors, 2012,121.

DOI:10.3390/s120101042      URL     PMID:22368510      [本文引用: 2]

A method for testing electronic instrument transformers is described, including electronic voltage and current transformers (EVTs, ECTs) with both analog and digital outputs. A testing device prototype is developed. It is based on digital signal processing of the signals that are measured at the secondary outputs of the tested transformer and the reference transformer when the same excitation signal is fed to their primaries. The test that estimates the performance of the prototype has been carried out at the National Centre for High Voltage Measurement and the prototype is approved for testing transformers with precision class up to 0.2 at the industrial frequency (50 Hz or 60 Hz). The device is suitable for on-site testing due to its high accuracy, simple structure and low-cost hardware.

王佳颖, 郭志忠, 张国庆 , 等.

电子式电压互感器暂态特性仿真与研究

[J]. 电力自动化设备, 2012(3):62-65,75.

[本文引用: 2]

Wang Jiaying, Guo Zhizhong, Zhang Guoqing , et al.

Electronic voltage transformer transient simulation and research

[J]. Electric Power Automation Equipment, 2012(3):62-65, 75.

[本文引用: 2]

International Electrotechnical Commission

IEC60044-7 Electronic voltage transformer

[S]. Geneva, Switzerland: IEC, 1999.

[本文引用: 2]

张超, 徐国顺 .

电力电容器等效电路模型和参数辨识方法的研究

[J]. 低压电器, 2013(5):10-13,19.

[本文引用: 1]

Zhang Chao, Xu Guoshun .

Research on equivalent model and parameter identification of power capacitor

[J]. DIYA DIANQI, 2013(5):10-13, 19.

[本文引用: 1]

张泽厚 .

电容器等效电路方式选择

[J]. 电子元件与材料, 1994(6):57-58.

Zhang Zehou .

Capacitor equivalent circuit mode selection

[J]. Electron Component Mater, 1994(6):57-58.

陈海鸥 .

电力系统重合闸动作时限的选择

[J]. 电工技术杂志, 1995(4):20-21.

[本文引用: 1]

Chen Haiou .

Power system reclosure time selection[J]

Electric Engineering, 1995(4):20-21.

[本文引用: 1]

郭晓丽, 陆小丽, 张建生 .

电力系统自动重合闸动作时限的选择

[J]. 南通工学院学报, 2000(S1):12-13.

[本文引用: 2]

Guo Xiaoli, Lu Xiaoli, Zhang Jiansheng .

Power system reclosure time selection

[J]. Journal of Nantong Institute of Technology, 2000(S1):12-13.

[本文引用: 2]

王晓慧 .

提高农村小水电网并大网重合闸成功率的研究

[D]. 长沙:湖南大学, 2011.

[本文引用: 1]

索南加乐, 梁振锋, 宋国兵 .

自适应熄弧时刻的单相重合闸的研究

[J]. 电力系统保护与控制, 2012(5):37-41.

[本文引用: 1]

Suo Nanjiale, Liang Zhenfeng, Song Guobing .

Study of single-phase reclosure with adaptive secondary arc extinction

[J]. Power System Protection and Control, 2012(5):37-41.

[本文引用: 1]